Error code analysis and selection principle of M-ary modulation in network-based control systems
来源期刊:中南大学学报(英文版)2016年第6期
论文作者:尹逊和 赵顺利 魏学业 H. K. LAM
文章页码:1372 - 1382
Key words:network-based control system; asynchronous dynamic system (ADS); M-ary modulation; delay; error code; linear matrix inequality (LMI)
Abstract: Error codes induced by M-ary modulation and modulation selection in network-based control systems are studied. It is the first time the issue of error codes induced by M-ary modulation is addressed in control field. In network-based control systems, error codes induced by noisy channel can significantly decrease the quality of control. To solve this problem, the network-based control system with delay and noisy channel is firstly modeled as an asynchronous dynamic system (ADS). Secondly, conditions of packet with error codes (PEC) loss rate by using M-ary modulation are obtained based on dynamic output feedback scheme. Thirdly, more importantly, the selection principle of M-ary modulation is proposed according to the measured signal-to-noise ratio (SNR) and conditions of PEC loss rate. Finally, system stability is analyzed and controller is designed through Lyapunov function and linear matrix inequality (LMI) scheme, and numerical simulations are made to demonstrate the effectiveness of the proposed scheme.
J. Cent. South Univ. (2016) 23: 1372-1382
DOI: 10.1007/s11771-016-3189-7

ZHAO Shun-li(赵顺利)1, YIN Xun-he(尹逊和)1, WEI Xue-ye(魏学业)1, H. K. LAM2
1. School of Electronic and Information Engineering, Beijing Jiaotong University, Beijing 100044, China;
2. Department of Informatics, King’s College London, London WC2R 2LS, U. K
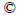 Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Abstract: Error codes induced by M-ary modulation and modulation selection in network-based control systems are studied. It is the first time the issue of error codes induced by M-ary modulation is addressed in control field. In network-based control systems, error codes induced by noisy channel can significantly decrease the quality of control. To solve this problem, the network-based control system with delay and noisy channel is firstly modeled as an asynchronous dynamic system (ADS). Secondly, conditions of packet with error codes (PEC) loss rate by using M-ary modulation are obtained based on dynamic output feedback scheme. Thirdly, more importantly, the selection principle of M-ary modulation is proposed according to the measured signal-to-noise ratio (SNR) and conditions of PEC loss rate. Finally, system stability is analyzed and controller is designed through Lyapunov function and linear matrix inequality (LMI) scheme, and numerical simulations are made to demonstrate the effectiveness of the proposed scheme.
Key words: network-based control system; asynchronous dynamic system (ADS); M-ary modulation; delay; error code; linear matrix inequality (LMI)
1 Introduction
In network-based control systems, measurements are quantized or coded by quantizer before transmission. This process can be accomplished by a component called analogue-to-digital (A/D) converter (see Fig. 1). y(t) is the output of the sensor while y(k) the output of the A/D is converter and  is the input of the controller. Similarly, u(k) is the output of the controller while u(t) is the output of the analogue-to-digital (D/A) converter. The network delay at the instant k is denoted by τk in Fig. 1. To simplify analysis, delay only in feedback path is considered. This is reasonable as the network only exists in the feedback path in many cases, such as vehicle control system [1], quantizer design [2] and wireless networked control systems [3].
is the input of the controller. Similarly, u(k) is the output of the controller while u(t) is the output of the analogue-to-digital (D/A) converter. The network delay at the instant k is denoted by τk in Fig. 1. To simplify analysis, delay only in feedback path is considered. This is reasonable as the network only exists in the feedback path in many cases, such as vehicle control system [1], quantizer design [2] and wireless networked control systems [3].
The coded digital signal (in bits) cannot usually be transmitted in the channel without any further processing. Modulation, a process of conveying a message signal inside another signal that can be physically transmitted, is indispensable to solve this problem in data transmission. It is traditionally thought of as an ideal (or perfect) process, i.e., no error transmission, in most designs of network-based control systems [4-6]. In essence, modulation itself has an inescapable effect on
the real system design, such as error codes resulting from it due to the existence of channel noise, an intrinsic factor in systems. That is, is different from
is different from  due to the existence of the error transmission resulting from the noise in the channel in Fig. 1. In what follows, effect of error codes induced by modulation is illustrated. For a given plant dynamics in Fig. 1, i.e.,
due to the existence of the error transmission resulting from the noise in the channel in Fig. 1. In what follows, effect of error codes induced by modulation is illustrated. For a given plant dynamics in Fig. 1, i.e.,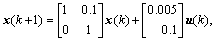 , where u(k)=K·x(k), a stabilizing state feedback gain is K=[8 5.6] by pole placement scheme given that the closed pole is p=[0.8 0.6]. Assume that the measured SNR is 6 dB in the channel. Hence, code error rate for binary amplitude shift keying (2ASK) is 4% according to code error rate
, where u(k)=K·x(k), a stabilizing state feedback gain is K=[8 5.6] by pole placement scheme given that the closed pole is p=[0.8 0.6]. Assume that the measured SNR is 6 dB in the channel. Hence, code error rate for binary amplitude shift keying (2ASK) is 4% according to code error rate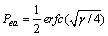 [7], where
[7], where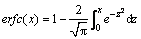 is the complementary error function, and γ is the SNR of the channel.
is the complementary error function, and γ is the SNR of the channel.
The state responses are illustrated in Fig. 2. x1 and x2 are the states without error codes, while y1 and y2 are the states with error codes induced by 2ASK modulation. From Fig. 2, the states without error codes converge to the equilibrium at k=20 while the ones with error codes at k=40 s to converge to the equilibrium. Clearly, the control performance is deteriorated due to the effect of error codes on system evolution. So, the existence of modulation can render this a challenging task. However, very few researchers noticed this point in control field. For example, a more effective modulation used in smart grid, adaptive modulation, is developed in [8]. As a matter of fact, there is only one paper considering the error codes induced by modulation in network-based control systems among the existing literatures, as far as we know [9]. However, in Ref. [9], they focused on power consumption of a node in the wireless network-based control systems and it is formulated as a function of its sampling period, delay and code error probability induced by modulation. The specific modulation is selected by minimizing the power consumption function. Clearly, modulation is purely used to determine the minimum power without any treatments of error codes induced by it. Unlike Ref. [9], where modulation is used in minimizing energy data transmission, the control problem resulting from error codes induced by modulation is another important concern and a treatment versus error code induced by modulation and modulation selection principle are discussed in the following sections.
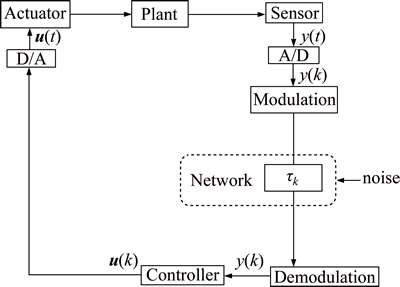
Fig. 1 Diagram of a network-based control system

Fig. 2 Effect of error codes on control systems
Modulation has different meanings between control and communication fields. It is necessary to clarify the difference between them at first. In general, the designers of control system focus on quantization perspective while communication engineers devote to the perspective of bandpass transmission.
Quantization, A/D block in Fig. 1, is a critical step when analog signals are transmitted over a digital channel in bandpass transmission. This scheme is similar to that of analog signal used in computer control systems. Hence, the design of quantizer is significant and has been widely studied in network-based control systems [10-12]. Due to space limitations, here design of quantizer will not be discussed. However, one kind of quantization, delta modulation, the simplest form of differential coding, should be explicitly discussed because of its name and interesting origin. The reason why this scheme is not called delta quantization or delta coding but delta modulation is that it is studied from the perspective of modulation at the beginning, and this term is passed down to date. In essence, delta modulation should be seen as a special form of quantizer or coder because this modulation scheme not only has the property of quantization, but the function of coding. Unlike general quantization schemes, delta modulation quantizes the difference between current and previous analog signal rather than the absolute value of analog signal itself. Delta modulation, hence becomes a highly effective quantizer or coder in signal processing and data compression as data capacity can be considerably decreased in comparison to that of quantizing the absolute value of original signals.
Modulation in telecommunication is a process of conveying a useful signal, for example, a digital bit stream or an analog audio signal, modulated by another signal that can be fit for telecommunication, see modulation block in Fig. 1. Therefore, modulation in communication can be categorized into two types: analog modulation and digital modulation, based on the property of modulated signals. However, due to bandpass characteristics of physical channels, baseband transmission, a way of bit stream transmission, is no longer effective. In this setting, baseband signals should be modulated to adapt channel profiles in advance. Hence, modulation becomes an underlying technique for bandpass transmission. This is why we consider it in this work. It is worth noting that this modulation is a way of signal transmission compared to delta modulation that is a way of quantization or coding.
Error codes in data transmission, in general, are measured by check code and discarded if no error correcting codes are applied. It is similar to that of active packet dropout scheme in congestion control of network [13-14]. This dropout scheme is widely used in real-time control systems as retransmission or error correcting strategy will consume much time, which will degrade the real-time performance of network-based control systems. Nevertheless, this method is used at the expense of quality of control. It is worth noting that the error codes discarded can be seen as active packet dropout, correspondingly, active packet loss rate can be replaced by code error rate (CER). Based on this idea, in our former paper [15], the impact of code error on network-based control systems with binary modulation is studied. However, binary modulation is the simplest one in modulation. It is nearly abandoned in real system design due to its low bandwidth utility. It is found that there need more efforts to do in designing practically efficient network-based control systems. The use of M-ary modulation is one of possibilities in real system design. However, introduction of M-ary modulation raises many new problems, such as determining the bounds on packet with error codes (PEC) loss rate for M-ary modulation and the type of modulation used. These issues will be solved in the following sections. The detailed contributions of this paper are depicted as follows.
First, the network-based control system with delay and noisy channel is modeled as an asynchronous dynamic system (ADS), a hybrid model, based on the idea that error code rate can be replaced by packet loss rate. Second, bounds on PEC loss rate with M-ary modulation are obtained based on dynamic output feedback scheme below which the design of controller is possible, which is very valuable in practical system design. Third, more importantly, the selection principle of M-ary modulation is proposed according to the measured signal-to-noise ratio (SNR) and conditions of PEC loss rate. In real system design, selecting appropriate modulation is inevitable, and this selection principle may be helpful for the engineers in constructing network-based control systems. In addition, controller is designed in terms of linear matrix inequality (LMI). The benefit of this approach is that the problem can be efficiently solved by interior-point methods with a guarantee that the global optimum will be found.
2 System dynamics
Consider a linear time-invariant dynamical system described in the following:
 (1)
(1)
where is the N-dimensional system state;
is the N-dimensional system state;  is the M-dimensional control input;
is the M-dimensional control input;  is the R-dimensional system output; and A, B, C are system gain matrices of appropriate dimensions.
is the R-dimensional system output; and A, B, C are system gain matrices of appropriate dimensions.
To facilitate system analysis and design, the following assumptions are made:
Assumption 1: Sensors are time-driven, while controller and actuators are event-driven. This assumption avoids latency compared to time-driven controller and actuators.
Assumption 2: Assume that delay is smaller than a sampling period T. Thus, the delay can be denoted as τk
Remark 1: To exclusively study the effect of error codes induced by modulation on network-based control systems, the case that the packet loss in propagation does not exist is assumed here. However, the PEC is actively discarded after error checking at the receiver in the paper. Hence, the PEC loss considered in this paper is different from the usual packet loss (i.e. passive packet loss), which results from heavy traffic load or unreliable transmission in network-based control systems.
Remark 2: Note that channel noise is different from the noise of control systems themselves even though they all possess a random characteristic. The former affects control systems, not directly but indirectly through error codes produced by encoder, while the latter is the inherent noise, which cannot be filtered in advance in control system design. Hence, digital transmission has a better performance of communication than that of analog one, and has been widely used in data transmission.
3 Communication channel
Based on the assumptions in Section 2, it is clear that transmission delay is the main concern in the paper as processing delay, propagation delay and calculating delay are ignored. In this section, transmission delays with different modulations are calculated at first. Then, CER, the most important representative of noisy channel, is discussed under different modulations.
3.1Time delay
Transmission delay is the amount of time required to push all of the bits of a packet into the channel. In other words, it is the one caused by the data-rate of channel and packet size. A similar result is found in Ref. [8]. Suppose that there are B bits ready to be pushed into the channel in each sampling period. It is assumed that symbol rate (or baud rate) is R symbols per second, while each symbol contains b bits information, e.g., a binary phase shift keying (BPSK) symbol contains 1 bit information and an M-ary phase shift keying (MPSK) symbol contains log2M bits information. So, transmission delay at sampling instant k can be denoted as
 (s) (2)
(s) (2)
Remark 3: τk is inversely proportional to b as total bits B and symbol rate R are fixed in each sampling period. So, τk is definite if b is determined. Obviously, τk is dependent on modulation as b is fully determined by modulation. In this setting, τk will be reduced when M-ary modulation is selected as one symbol in M-ary modulation contains more bits. Hence, M-ary modulation is of realistic significance to decrease the effect of delay on the design of network-based control systems.
3.2 Noisy channel and M-ary modulation
In communication systems, noise is an error or unwanted random disturbance for a useful signal in a communication channel. It is, however, different from interference as it still exists in channels although there is no useful signal in transmission. In digital communication systems, a certain SNR will result in a certain CER [7]. Consequently, code error can be used to character noise. In general, cyclic redundancy check (CRC) is used to detect code error in real communication systems. But, how to recover the error codes is another complex problem, and it may consume more time and energy. In this paper, we assume that no error correcting code and re-transmission schemes are used due to real-time consideration in network-based control systems.
In the receiver side, the mixture of useful signals and noise is received, and signals received possesses random characteristic because of the random property of noise. The effect of noise can be converted into code error in the process of demodulation. The signals with error codes are decoded and used by controller if no error correcting code is used. This will result in reduction of performance of control systems (please see Section 1). Hence, to avoid error bits, the PEC detected by CRC can be discarded in advance in this paper. In this context, controller will use the data transmitted in the last period and the effect of zero-order holder (ZOH) scheme is then considered to calculate control commands.
In binary bandpass transmission, each symbol contains one bit information, which is low efficient for resource-limited communication systems. A better way to solve this issue is to enable each symbol to contain more bits. That is why the M-ary modulation is used in this paper. However, the introduction of M-ary modulation will introduce new challenges. For example, M-ary modulation consumes more energy to obtain an equal SNR compared to binary modulation. In addition, the complexity of equipment will exponentially increase along with the increase of the bits of each symbol.
There are usually three types of modulations in M-ary modulation, i.e., M-ary amplitude shift keying (MASK), M-ary frequency shift keying (MFSK) and MPSK. CER of each modulation with coherent demodulation for a prescribed M (M=2k (k=1, 2…)) is listed as below [7].
CER of MASK:
 (3)
(3)
Similarly, CER of MFSK can be denoted as:
 (4)
(4)
and CER of MPSK is:
 (5)
(5)
where γ denotes the SNR for a specific modulation;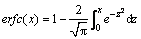 is the complementary error function and π is the ratio of the circumference.
is the complementary error function and π is the ratio of the circumference.
Remark 4: For a given channel frequency band, the utilization of frequency band of each modulation will be increased if M increased. However, another important performance index, reliability, must be considered. That is, the level of CER should satisfy the requirement of communication systems, which is related to the selected modulation. In essence, the reliability of communication system with M-ary modulation can be improved at the expense of power consummation and increased design complexity compared to binary modulation [7].
4 Stability analysis and controller design
In this section, the network-based control system with time delay and error code is modeled as an ADS at first. Then, bounds on PEC loss rate is given. Finally, stability analysis is made and controller is designed based on Lyapunov function and LMI scheme.
4.1 Dynamic output feedback control and ADS system model
Discretizing (1) with sampling period T, then the network-based control systems with time delay can be written as
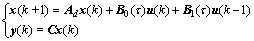 (6)
(6)
where


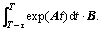
In practical applications, states, in general, are not fully measured. But, a part of states can be measured. To fully use the partial states, dynamic output feedback control scheme [19] is utilized to stabilize network-based control systems. The discrete dynamic output feedback controller used in Eq. (6) can be written as
 (7)
(7)
The measurements of sensor are said to be transmitted successfully if they are received and used by controller, otherwise, packet loss occurs. The network-based control systems (6) with code error can be modeled as an ADS. Let the augmented state be 
 in Eqs. (6) and (7), the ADS model of closed-loop system can be obtained:
in Eqs. (6) and (7), the ADS model of closed-loop system can be obtained:
 (8)
(8)
where
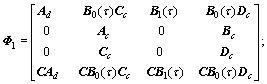
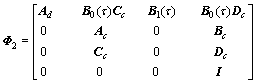 .
.
 is the system matrix when the packet is successfully used in the controller, while
is the system matrix when the packet is successfully used in the controller, while  is the one for the case of PEC dropout.
is the one for the case of PEC dropout.
4.2 Bound on PEC loss rate
Similar to the Theorem 5.4 in Ref. [20], the bound on PEC loss rate with M-ary modulation is given as in the follows.
Theorem 1: The bound on PEC loss rate making the network-based control system stable, denoted as  to avoid confusion with CER, should satisfy the following conditions.
to avoid confusion with CER, should satisfy the following conditions.
1) The closed-loop system is exponentially stable for all  in MASK,
in MASK, in MFSK and
in MFSK and  in MPSK, if the open-loop system is marginally stable.
in MPSK, if the open-loop system is marginally stable.
2) The closed-loop system is exponentially stable for all in MASK,
in MASK, 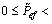
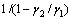 in MFSK and
in MFSK and  in MPSK, where
in MPSK, where 
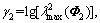 if the open-loop system is unstable.
if the open-loop system is unstable.
Proof: The closed-loop system is exponentially stable for all transmission rates of data less than or equal to one (0 in MASK,
in MASK,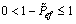 in MFSK and
in MFSK and  in MPSK, if the open-loop system is marginally stable. The inequalities can be further rewritten as
in MPSK, if the open-loop system is marginally stable. The inequalities can be further rewritten as  in MASK,
in MASK, in MFSK and
in MFSK and  in MPSK. So, 1) is proved. Similarly, the closed-loop system is exponentially stable for all
in MPSK. So, 1) is proved. Similarly, the closed-loop system is exponentially stable for all 
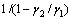 in MASK,
in MASK, 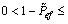
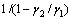 in MFSK and
in MFSK and  in MPSK, where γ1=
in MPSK, where γ1= 
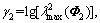 if the open-loop system is unstable. The inequalities above can also be rewritten as 2). The proof of Theorem 1 is completed.
if the open-loop system is unstable. The inequalities above can also be rewritten as 2). The proof of Theorem 1 is completed.
Remark 5: Equations (3), (4) and (5) hold when M is large enough. In reality, an infinite M is impossible due to the current technique of hardware design. A certain conservative is thus introduced because of the constraints on M. How to select M will be discussed in Section 5.
4.3 Related definitions and lemmas
Definition 1: An ADS is said to be exponentially stable if there exists a constant α such that:
 (9)
(9)
where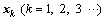 denotes system states; ||·|| means the Euclidean norm.
denotes system states; ||·|| means the Euclidean norm.
Lemma 1 [21]: For an ADS, if there exists a Lyapunov function V: 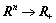 and V satisfies
and V satisfies  where
where 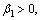
 and there exist scalars α>0,
and there exist scalars α>0, 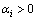 (i=1, …, N), such that:
(i=1, …, N), such that:  and
and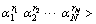 α>1, where
α>1, where  (s=1, …, N) denotes the occurrence rate for each subsystem. Then, this ADS is exponentially stable with decay rate α.
(s=1, …, N) denotes the occurrence rate for each subsystem. Then, this ADS is exponentially stable with decay rate α.
Schur complement lemma [22]: Consider a symmetric matrix X that can be partitioned into blocks:
 (10)
(10)
where both A and C are symmetric, square and negative semi-definite, then the following properties are equivalent:
1) X is negative semi-definite.
2) The schur complement of C in X, denoted as  , is negative semi-definite.
, is negative semi-definite.
3) The schur complement of A in X, denoted as  , is negative semi-definite.
, is negative semi-definite.
4.4 Stability analysis
Theorem 2: Closed-loop network-based control system modeled as ADS (8) with PEC loss rate 1-P is said to be asymptotically stable if there exist asymmetric positive definite matrices P, Q, S, Z, controller gain matrix Ac, Bc, Cc, Dc with appropriate dimensions and scalars α1, α2,and α satisfy the following inequalities:
 (11a)
(11a)
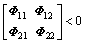 (11b)
(11b)
 (11c)
(11c)
where



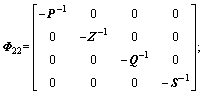

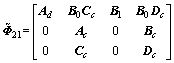 ;
;
 ;
;
 .
.
Proof: Let 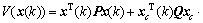
 obviously,
obviously,  0 as P, Q, S and Z are positive definite matrices.
0 as P, Q, S and Z are positive definite matrices.
When data packets are successfully used, we have and “*” denotes the symmetric entries.
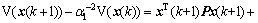


where
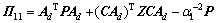 ;
;
 ;
;

 ;
;
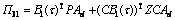 ;
;
 ;
;
 ;
;
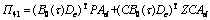 ;
;
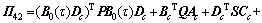
 ;
;
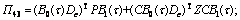
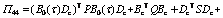
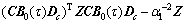
From Lyapunov stability theory, the following inequality holds
 (12)
(12)
Note that the inequality (12) can be rewritten as
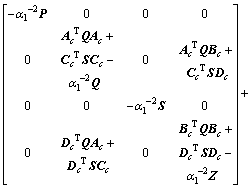
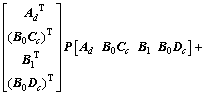
 .
.
By Schur complement lemma (3), the following inequality is obtained
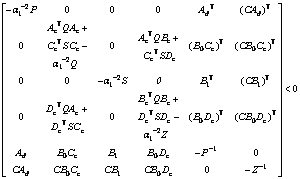
Similarly, Schur complement lemma (3) is used again, the inequality (12) can be finally written as
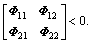
Until now, the inequality (11b) is obtained.
In addition, the proof of the inequality (11c), i.e., the case of PEC loss, is the same as that of inequality (11b) and thus is omitted.
4.5 Controller parameter design
Note that inequalities (11b) and (11c) are not LMIs. In order to obtain feasible LMIs, (11b) is premultiplied and postmultiplied by 
 while (11c) is premultiplied and postmultiplied by
while (11c) is premultiplied and postmultiplied by and let
and let 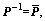





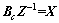 and
and  . We can obtain:
. We can obtain:
 (13a)
(13a)
 (13b)
(13b)
 (13c)
(13c)
where
 ;
;
 ;
;
 ;
;
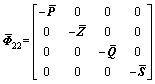 ;
;
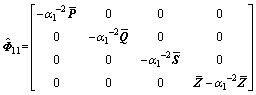 ;
;
 ;
;
 ;
;
 .
.
Obviously, parameters in Eq. (7)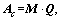

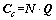 and
and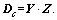 These parameters can be solved by LMI toolbox.
These parameters can be solved by LMI toolbox.
5 M-ary modulation selection
In communication systems, modulation scheme is not arbitrarily selected. In general, big M has a high efficiency for the precious wireless channel source; meantime, it means an increasing complexity in hardware and software design, and further, the increasing cost of system design. So, how to make a trade-off between the modulation and the complexity of system design is an open issue to be solved.
In this part, the relation between system stability and the selection of M is investigated. Inspired by Theorem 1, we find the following theorem.
Theorem 3: The upper bound on M that makes the network-based control system with MFSK stable should satisfy the following conditions.
1) The closed-loop system is exponentially stable for all  in MFSK if the open-loop system is marginally stable.
in MFSK if the open-loop system is marginally stable.
2)The closed-loop system is exponentially stable for all  in MFSK if the open-loop system is unstable, where
in MFSK if the open-loop system is unstable, where 

Proof: From 1) in Theorem 1, the closed-loop system is exponentially stable for all 
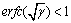 in MFSK if the open-loop system is marginally stable as
in MFSK if the open-loop system is marginally stable as  in Eq. (4). Then, the foregoing inequalities can be rewritten as
in Eq. (4). Then, the foregoing inequalities can be rewritten as  . So, 1) in Theorem 3 is obtained. Similarly, the closed-loop system is exponentially stable for all
. So, 1) in Theorem 3 is obtained. Similarly, the closed-loop system is exponentially stable for all 
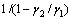 in MFSK if the open-loop system is unstable, where
in MFSK if the open-loop system is unstable, where
 Then, the inequalities above can be represented as
Then, the inequalities above can be represented as  in 2). Until now, the proof of Theorem 3 is completed.
in 2). Until now, the proof of Theorem 3 is completed.
Remark 6: In this theorem, only the selection theorem of MFSK is given. The other two modulations have no analytical solutions as the inverse of the complementary error function has no analytical one. Fortunately, numerical solutions can be available with the help of mathematical software in practical system design.
Remark 7: As the bound on PEC loss rate is closely related to system dynamics and the type of controller selected, M is further obtained based on the bound above. So this selection theorem should be re-deduced if the system dynamics and the controller are different.
6 Numerical illustrations
In this section, simple numerical simulations are given to demonstrate the effectiveness of the proposed algorithm. Without loss of generality, MFSK scheme is investigated here. Similar analysis can be done for MPSK and MASK.
In this simulation, network only exists between sensors and controller, information collected by sensors is transmitted after modulating and received by controller after demodulation. When the information arrives, controller computes control commands to manipulate actuator and plant.
The parameters of a linear time-invariant dynamical system (1) are given as follows:



Let the sampling period T be 10ms, and to facilitate the simulation, it is assumed that the measured SNR is 5.79 dB, and M=16 according to Theorem 3, note that different M′s will be picked under different levels of SNRs. In doing so, the CER for MFSK is  according to Eq. (4). Suppose that the baud rate R is 5 K baud, i.e., 5 K symbols per second. Assume that the length of a frame is 100 bits, in this context, delay of MFSK is 5ms according to Eq. (2). The initial state is
according to Eq. (4). Suppose that the baud rate R is 5 K baud, i.e., 5 K symbols per second. Assume that the length of a frame is 100 bits, in this context, delay of MFSK is 5ms according to Eq. (2). The initial state is 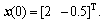 We choose α1=1.03 and α2=0.85 in Theorem 2, then α=1.028 by (11a).
We choose α1=1.03 and α2=0.85 in Theorem 2, then α=1.028 by (11a).
The control gains of the system with MFSK modulation can be obtained from inequalities (13a), (13b) and (13c).

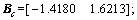
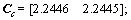

In Fig. 3, Packet=0 means that the packet is dropped due to code error, whereas Packet=1 denotes the packet without code error. This diagram only denotes the packet error or not, so the values between 0 and 1 are meaningless and will never be used. Controller will use the data stored in ZOH when the packet with code error is dropped.
The system states, x1 and x2, converge to the equilibrium, and control signals finally converge to zero for the case of in Fig. 4. That is, the network-based control system with MFSK modulation and noisy channel is stable. So, the proposed algorithm is reasonable and the designed controller is effective in the system design.
in Fig. 4. That is, the network-based control system with MFSK modulation and noisy channel is stable. So, the proposed algorithm is reasonable and the designed controller is effective in the system design.

Fig. 3 Packet error illustration

Fig. 4 State response and control signals with MFSK modulation and Pef=1%:
This network-based control system can run smoothly if CER (also known as packet loss rate) satisfies the constraints proposed in Theorem 1. Different CERs can result in different steady state performance. State responses and control signals with different CERs are illustrated in Figs. 5-6.
When the CER  see Fig. 5, the time the states used to converge to equilibrium is longer than that of the states with CER
see Fig. 5, the time the states used to converge to equilibrium is longer than that of the states with CER  in Fig. 4. Control signal needs nearly 20 sampling periods in Fig. 5 to converge to zero compare to about 10 sampling periods in Fig. 4.
in Fig. 4. Control signal needs nearly 20 sampling periods in Fig. 5 to converge to zero compare to about 10 sampling periods in Fig. 4.
The stability of this network-based control system continues to deteriorate when the CER falls to 14% in Fig. 6. The states and control signal need more than about 40s to converge to equilibrium.
Hence, the stability of network-based control system is closely related to CER caused by channel noise. In practical applications, the modulation used can be determined based on Theorem 3 if the CER is calculated and the SNR is measured. However, the bigger the modulation M is, the higher complexity is the system design.

Fig. 5 State response and control signals with MFSK modulation and Pef=5%:

Fig. 6 State response and control signals with MFSK modulation and Pef=14%:
7 Conclusions
1) In network-based control systems, error codes induced by noisy channel can significantly decrease the whole system performance. To solve this problem, the network-based control system with delay and noisy channel is firstly modeled as an ADS in view of the idea that PEC loss rate can be replaced by CER. Then, the bound on PEC loss rate that guarantees stability of system with M-ary modulation is given, and the principle of modulation selection that makes the system stable is also proposed. Finally, the stability of network-based control systems with modulation and noisy channel is analyzed, and the dynamic output feedback controller is designed by Lyapunov theory and LMI scheme. The effectiveness of the proposed scheme is demonstrated by numerical simulations. It is shown that network-based control systems with M-ary modulation and noisy channel can tolerate a certain code error.
2) Note that only MFSK scheme is investigated in the paper, however, similar analysis can be made of MPSK and MASK. Theorem 1 of the bound on PEC loss rate is conservative; however, this heuristic result has some values of guidance in design of network-based control systems with M-ary modulation. The scheme proposed in this paper can be extended to the other modulations, such as OFDM and QAM, to decrease the detrimental effect of modulation on the design of network-based control systems.
3) How to relax the conservative of Theorem 1 is an open problem. In addition, the selection principles of MASK and MPSK in Theorem 3 are difficult to be obtained. These issues may be solved in our further research.
References
[1] SEILER P, RAJA S. Analysis of communication losses in vehicle control problems [C]// IEEE Conference on American Control Conference. Arlington: IEEE, 2001: 1491-1496.
[2] NAIR G, EVANS R. Communication-limited stabilization of linear systems [C]// IEEE Conference on Decision and Control. Sydney: IEEE, 2000: 1005-1010.
[3] PAJIC M, MANGHARAM R, PAPPAS G J, SUNDARAM S. Topological conditions for in-network stabilization of dynamical systems [J]. IEEE Journal of Selected Area in Communication, 2013, 31(4): 794-807.
[4] TRIVELLATO M, BENVENUTO N. State control in networked control systems under packet drops and limited transmission bandwidth [J]. IEEE Transactions on Communications, 2010, 58(2): 611-622.
[5] TEIXEIRA A, SHAMES I, SANDBERG H, JOHANSSON K H. Distributed fault detection and isolation resilient to network model uncertainties [J]. IEEE Transactions on Cybernetics, 2014, 44(11): 2024-2037.
[6] LIU Ying-ying, CHU Yun-kai, CHE Wei-wei, LIU Yi-yang. Stability analysis and stabilization of wireless networked control systems based on deadband control scheduling [J]. Journal of Central South University, 2014, 21(11): 4228-4235.
[7] HAYKIN S. Communications systems [M]. New York: Wiley, 2001.
[8] LI Hu-sheng, SONG Ju-bin, ZENG Qi. Adaptive modulation in networked control systems with application in smart grids [J]. IEEE Communication Letters, 2013, 17(7): 1305-1308.
[9] SADI Y, ERGEN S C, PANGUN P. Minimum energy data transmission for wireless networked control systems [J]. IEEE Transactions on Wireless Communications, 2013, 13(4): 2163-2175.
[10] LIU Ying-ying, CHU Yun-kai, CHE Wei-wei. Guaranteed cost control of networked control systems under limited communication capacity and variable sampling [J]. Journal of Central South University, 2014, 21(3): 978-986.
[11] CHEN Hung-chi, CHEN Keng-yuan,CHEN Wei-yu. High-efficiency current control methods based on multidimensional feedback quantization and its application to three-phase PMSM [J]. IEEE Transactions on Automatic Control, 2014, 61(11): 5820-5829.
[12] YUKSEL S. Jointly optimal LQG quantization and control policies for multi-dimensional systems [J]. IEEE Transactions on Automatic Control, 2014, 59(6): 1612-1617.
[13] FAN Qiu, YUAN Xue. Robust jointcongestioncontroland scheduling for time-varying multi-hop wireless networks with feedback delay [J]. IEEE Transactions on Wireless Communications, 2014, 13(9): 5211-5222.
[14] VANDANA K, RATNESHWER G. Congestioncontrolfor high-speed wirednetwork: a systematic literature review [J]. Journal of Network and Computer Applications, 2014, 45: 62-78.
[15] ZHAO Shun-li, YIN Xun-he, WEI Xue-ye. Analysis and design of network-based control systems with binary modulation [J]. Mathematical Problems in Engineering, 2014, http://www.hindawi. com/journals/mpe/2014/785790/.
[16] YU Wen-wu, ZHOU Lei, YU Xing-huo, L Jin-hu, LU Ren-quan. Consensus in multi-agent systems with second-order dynamics and sampled data [J]. IEEE Transactions on Industrial Informatics, 2013, 9(4): 2137-2146.
Jin-hu, LU Ren-quan. Consensus in multi-agent systems with second-order dynamics and sampled data [J]. IEEE Transactions on Industrial Informatics, 2013, 9(4): 2137-2146.
[17] QIN Jia-hu, YU Chang-bin, GAO Hui-jun. Coordination for linear multi-agent systems with dynamic interaction topology in the leader-following framework [J]. IEEE Transactions on Industrial Electronics,2014, 61(5): 2412-2422.
[18] LIN Peng, REN Wei. Constrained consensus in unbalanced networks with communication delays [J]. IEEE Transactions on Automatic Control, 2014, 59(3): 775-781.
[19] JOHNSON T L, ATHANS M. On the design of optimal constrained dynamic compensators for linear constant system [J]. IEEE Transactions on Automatic Control, 1970, 15(6): 658-660.
[20] ZHANG Wei. Stability analysis of networked control systems [D]. Cleveland: Case Western Reserve University, 2001.
[21] RABELLO A, BHAYA A. Stability of asynchronous dynamical systems with rate constraints and application [J]. IEE Proceedings-Control Theory and Applications, 2003, 150(5): 546-550.
[22] BOYD S, VANDENBERGHE L. Convex optimization [M]. Cambridge: Cambridge University Press, 2004.
(Edited by DENG Lü-xiang)
Foundation item: Project(61172022) supported by the National Natural Science Foundation of China; Project(GDW20151100010) supported by the State Administration of Foreign Experts Affairs of China
Received date: 2015-03-23; Accepted date: 2015-09-23
Corresponding author: YIN Xun-he, Professor, PhD; Tel: +86-10-51684697; E-mail: xhyin@bjtu.edu.cn

