锈蚀钢筋混凝土梁的受弯分析模型
邢国华1, 2,牛荻涛1
(1. 西安建筑科技大学 土木工程学院,陕西 西安,710055;
2. 长安大学 建筑工程学院,陕西 西安,710061)
摘要:以锈损率较低的钢筋混凝土简支梁为对象,在平截面假定基础上,提出考虑钢筋、混凝土材料性能劣化和几何尺寸变化的受弯承载力计算公式;采用换算截面法计算锈蚀钢筋混凝土梁的等效刚度,给出考虑锈蚀钢筋、混凝土二者间黏结性能退化的有效刚度计算公式,建议锈蚀钢筋混凝土简支梁在集中荷载作用下跨中挠度的计算方法,并通过39根锈蚀钢筋混凝土梁的试验数据对建议受弯分析模型验证。研究结果表明:锈蚀钢筋混凝土梁受弯承载力试验值与计算值之比的平均值为1.100,方差为0.041,二者吻合较好;多数锈蚀试件按受弯分析模型计算得到的荷载-跨中挠度曲线与试验曲线吻合较好,变化趋势相当,建议受弯分析模型可为锈蚀钢筋混凝土梁的全过程受力分析提供参考。
关键词:黏结;锈蚀;受弯性能;梁;有效刚度
中图分类号:TU375.1 文献标志码:A 文章编号:1672-7207(2014)01-0193-09
Analytical model of flexural behavior of corroded reinforced concrete beams
XING Guohua1, 2, NIU Ditao1
(1. School of Civil Engineering, Xi’an University of Architecture & Technology, Xi’an 710055, China;
2. School of Civil Engineering, Chang’an University, Xi’an 710061, China)
Abstract: By selecting reinforced concrete beams of lower corrosion rates as research object, a calculation formula of flexural baring capacity of corroded reinforced concrete beams was put forward based on the plane section assumption. Furthermore, a theoretical expression of equivalent stiffness of corroded reinforced concrete beam was suggested by using transformed section approach. The weakening of the bond between concrete and reinforcement was considered in this method. In addition, a theoretical formula of mid-span deflection of corroded reinforced concrete simply supported beams subjected to a four-point bending was proposed. The analytical model was verified using 39 corroded reinforced concrete beams. Good agreement between test results and prediction results for flexural baring capacity is achieved with an average ratio of test results to predicted results being 1.100 and the variance being 0.041. The trends of the test load-mid span deflection curves and the predicted curves are much the same. Thus, the suggested model can be served as a reference for full-range analysis of corroded reinforced concrete beams.
Key words: bond; corrosion; flexure behaviour; beam; effective stiffness
混凝土中的钢筋锈蚀是造成混凝土结构耐久性损伤的最主要因素[1],它造成结构的破坏主要表现为受力材料性能劣化、几何尺寸变化和钢筋与混凝土二者间黏结性能退化3个方面。钢筋混凝土锈蚀构件合理受力分析模型的提出应考虑以上3个方面因素的影响。钢筋混凝土梁是混凝土结构的重要受力构件,研究锈蚀钢筋混凝土梁的受弯性能是进行钢筋混凝土结构耐久性评估及耐久性设计的关键问题[2]。为此,国内外学者开展了大量的试验研究、理论分析与数值模拟,取得了丰硕的研究成果。Rodriguez等[3]采用室内快速锈蚀试验分析了锈蚀钢筋混凝土梁的受弯性能,指出锈蚀不严重的钢筋混凝土梁仍发生延性受弯破坏。此后,Mangat等[4-5]对锈蚀钢筋混凝土梁进行了研究,结果表明钢筋锈蚀后混凝土与钢筋间黏结性能退化是引起抗弯强度降低的重要原因。Malumbela等[6]对持载作用下锈蚀钢筋混凝土梁进行了系统试验研究,结果表明锈蚀钢筋1%的质量损失率将导致锈蚀构件受弯承载力降低约0.7%。Azad等[7]对56根钢筋混凝土梁进行加速锈蚀试验,建议了锈蚀钢筋混凝土梁残余抗弯强度的设计计算方法。金伟良等[2, 8-9]对锈蚀钢筋混凝土梁的受弯性能进行了试验研究和理论分析,通过引入锈蚀钢筋与混凝土的协同工作系数来计算锈蚀构件的抗弯强度。朱荻涛等[10]在以往锈蚀梁破坏试验研究基础上,立足于工程应用,建立了锈蚀梁的受弯承载力实用计算模型。从以上分析可以看出:以往研究重点分析锈蚀钢筋混凝土的抗弯强度,对锈损构件的变形性能鲜有涉及。孙彬等[11]采用刚度解析法对黏结力退化后锈蚀钢筋混凝土梁的截面刚度进行了理论分析,建立了锈蚀钢筋混凝土梁抗弯刚度的计算模型。王晓刚等[12]通过类似的研究方法,建立了锈损构件的短期刚度计算公式。以上研究均是在完好钢筋混凝土构件短期刚度计算公式基础上,通过引入综合应变系数来考虑钢筋锈蚀的影响,建立的刚度计算公式经验性较强,是衡量锈蚀构件变形能力的指标之一,仅适用于锈蚀构件的适用性评估,尚不能用于锈损构件的全过程分析。此外,由于影响锈蚀钢筋混凝土梁变形性能的因素较多,仅通过综合应变系数单一参数来表征略显不足。本文作者分析了锈蚀钢筋混凝土梁受弯性能退化的影响因素及机理,通过整理大量锈损率较低的锈蚀钢筋混凝土梁的试验研究数据,综合考虑钢筋锈蚀造成受弯构件材料性能劣化、几何尺寸变化和黏结性能退化三方面影响,提出了锈蚀钢筋混凝土梁荷载-跨中挠度计算模型,并通过39组试验数据对其验证。
1 锈蚀钢筋混凝土梁抗弯性能
1.1 锈损构件中材料性能变化
(1) 锈蚀钢筋的力学性能。通过对242根锈蚀钢筋[1]试验数据统计分析,本文作者建议锈蚀钢筋的名义屈服强度按下式计算:
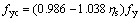 (1)
(1)
式中:fyc为锈蚀钢筋的屈服强度;fy为未锈钢筋的屈服强度;ηs为锈蚀钢筋的截面损失率。
钢筋锈蚀后造成的截面面积减小在锈损构件受力分析较易考虑,锈蚀钢筋的变形性能下降则较难分析。文献[13]综合考虑均匀锈蚀和蚀坑锈蚀2种情况,建议按下式计算锈蚀钢筋的极限应变:
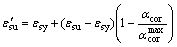 (2)
(2)
式中: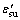 为锈蚀钢筋极限应变;
为锈蚀钢筋极限应变;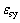 为未锈钢筋屈服应变;
为未锈钢筋屈服应变;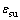 为未锈钢筋极限应变;
为未锈钢筋极限应变;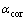 为锈蚀钢筋截面损失系数,
为锈蚀钢筋截面损失系数,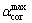 为截面损失系数的最大值,建议取0.5。
为截面损失系数的最大值,建议取0.5。
(2) 混凝土的力学性能。钢筋锈蚀将产生体积膨胀,内部微裂缝的存在导致混凝土强度降低,同时会致使混凝土保护层沿筋开裂,从而使混凝土截面产生几何损伤。后者在受力分析时可通过忽略保护层厚度来考虑,钢筋锈蚀导致微裂缝发展,进而致使混凝土抗压强度降低[14]可通过下式计算:
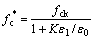 (3)
(3)
式中:fc*为混凝土软化抗压强度;fck为混凝土抗压强度标准值;K为钢筋表面粗糙度与直径的相关系数,取0.1;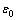 为混凝土峰值抗压强度对应的混凝土压应变,一般取0.002;
为混凝土峰值抗压强度对应的混凝土压应变,一般取0.002;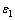 为开裂混凝土的广义平均拉应变,通常应小于0.01,计算式[13]为
为开裂混凝土的广义平均拉应变,通常应小于0.01,计算式[13]为
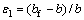 (4)
(4)
b为未锈蚀构件的截面宽度;bf为锈蚀构件的截面宽度。通常锈蚀构件的截面宽度变化可通过下式计算:
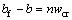 (5)
(5)
式中:n为锈蚀构件受压纵筋数量;wcr是锈蚀深度为X时锈蚀构件裂缝总宽度,文献[15]建议其计算式为
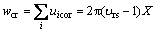 (6)
(6)
uicor为锈蚀构件中第i条裂缝的宽度;υrs为钢筋锈蚀后的氧化物体积与未锈蚀时相应材料的体积之比,文献[15]假定锈蚀物均匀分布于钢筋表面且不可压缩,此时υrs取2.0。根据这一假定,锈蚀深度X和锈蚀钢筋的截面损失率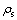 存在如下关系式:
存在如下关系式:
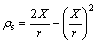 (7)
(7)
式中:r为钢筋未锈蚀时其半径。
(3) 钢筋与混凝土间的黏结性能。El Maaddawy等[16]对锈蚀钢筋混凝土构件受力性能分析时指出,当作用弯矩小于开裂弯矩Mcr时,钢筋应变与混凝土应变一致,没有滑移产生,可不考虑锈蚀造成的黏结性能下降;当作用弯矩大于开裂弯矩Mcr时,应考虑钢筋锈蚀造成的黏结性能劣化。在CEB-FIP模式规范[17]建议的本构模型基础上,对于锈蚀钢筋混凝土构件,通过修正最大黏结应力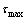 以及参数s1和s2而获得锈蚀钢筋与混凝土界面的黏结应力-滑移本构模型,如图1所示。图1中,由钢筋与混凝土之间的摩擦力主导的黏结应力
以及参数s1和s2而获得锈蚀钢筋与混凝土界面的黏结应力-滑移本构模型,如图1所示。图1中,由钢筋与混凝土之间的摩擦力主导的黏结应力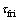 (也是下限值)根据混凝土是否受到有效约束取为0.15~0.40倍
(也是下限值)根据混凝土是否受到有效约束取为0.15~0.40倍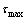 。
。
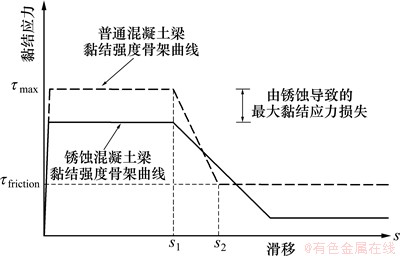
图1 建议的黏结应力-滑移本构模型
Fig. 1 Proposed bond stress-slip model
1.2 锈蚀钢筋混凝土梁的破坏特征分析
试验研究[8]表明:锈蚀梁的受力过程仍可分为3个阶段。当梁承受的弯矩较小时,构件处于弹性工作状态,有锈蚀裂缝存在,但挠度较未锈梁稍大。随着荷载继续增大,受拉区出现垂直裂缝,即认为第1阶段结束。受拉区一旦开裂,荷载挠度曲线出现转折点,挠度增长加快,挠度大于正常梁。随荷载增大,裂缝宽度加大,中和轴上移,压区混凝土出现塑性变形,进而受拉钢筋屈服,第2阶段结束。受拉钢筋屈服后,中和轴上移,受压区混凝土压碎,梁发生破坏。
2 锈蚀钢筋混凝土梁的受弯承载力
钢筋的力学性能对钢筋混凝土构件的受力性能影响显著,特别是对于锈蚀钢筋混凝土梁,钢筋的变形性能及钢筋用量控制着受弯构件的破坏模式。已有研究表明[1]:随着锈蚀量增大,钢筋的屈服平台逐渐缩短,当锈蚀率大于20%时,屈服台阶已基本丧失。
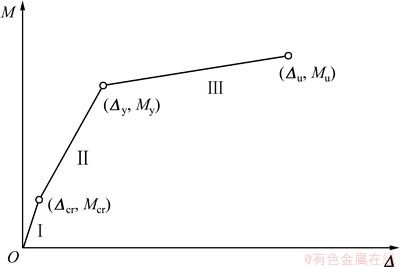
图2 锈蚀梁受力阶段示意图
Fig. 2 Schematic model of moment deflection curve
因此,本文主要选取钢筋锈蚀率小于20%的锈蚀梁进行受弯分析。对于此类锈蚀钢筋混凝土梁,其受力过程仍可分为3个阶段:弹性阶段、裂缝阶段和破坏阶段。受力过程示意图见图2。图2中,Mcr,My和Mu分别为锈蚀梁开裂弯矩、屈服弯矩、极限弯矩;△cr,△y和△u分别为锈蚀梁开裂挠度、屈服挠度、极限挠度。
2.1 弹性阶段
当梁承受较小弯矩时,构件处于弹性工作状态,钢筋锈蚀率并不影响混凝土梁的开裂荷载[2]。因此,锈蚀钢筋混凝土梁(几何尺寸如图3所示)的开裂弯矩Mcr可按下式计算:
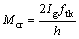 (8)
(8)
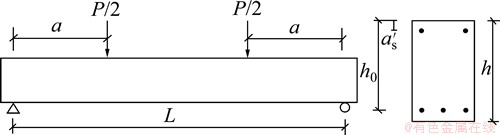
图3 简支梁截面尺寸
Fig. 3 Dimensions and cross section of simply supported beam
式中:Ig为未开裂截面的惯性矩,为bh3/12;b为截面宽度;h为截面高度;ftk为混凝土抗拉强度。
2.2 裂缝阶段
对于锈蚀率相对较低的锈蚀钢筋混凝土梁,其截面平均应变基本上仍符合平截面假定[16],忽略受拉区混凝土抗拉能力,矩形梁截面应力分布如图4所示。
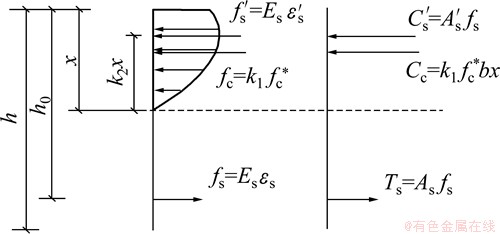
图4 矩形梁截面应力及其合力
Fig. 4 Stresses and forces of beam cross section
根据截面分析法,可得图4中受压区混凝土压应力的合力Cc为:
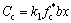 (9)
(9)
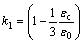 (10)
(10)
式中: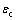 为混凝土压应变;x为混凝土受压区高度;fc*为混凝土软化抗压强度,按式(3)计算;b为矩形梁截面宽度。
为混凝土压应变;x为混凝土受压区高度;fc*为混凝土软化抗压强度,按式(3)计算;b为矩形梁截面宽度。
受压区混凝土合力产生的弯矩Mc为:
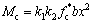 (11)
(11)
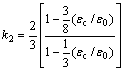 (12)
(12)
一般情况下,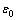 可取0.002,故
可取0.002,故
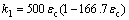 (13)
(13)
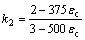 (14)
(14)
当锈蚀梁受拉纵筋屈服时,根据平截面假定,受压钢筋应变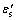 、混凝土压应变
、混凝土压应变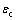 分别为:
分别为:
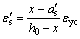 (15)
(15)
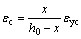 ≤0.003 3 (16)
≤0.003 3 (16)
式中: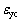 为锈蚀钢筋的屈服应变,可由式(1)获得屈服强度fyc后除以弹性模量计算得到。
为锈蚀钢筋的屈服应变,可由式(1)获得屈服强度fyc后除以弹性模量计算得到。
式(15)和式(16)中混凝土受压区高度x可通过下式确定:
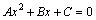 (17)
(17)
式中:
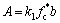 (18)
(18)
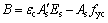 (19)
(19)
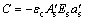 (20)
(20)
因此,忽略受拉区混凝土的拉力作用后,锈蚀梁跨中截面的名义屈服弯矩My为:
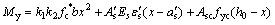 (21)
(21)
式中: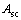 为锈蚀受拉钢筋的截面面积,可通过未锈钢筋截面面积As乘以截面锈蚀率计算获得;h0为截面有效高度;
为锈蚀受拉钢筋的截面面积,可通过未锈钢筋截面面积As乘以截面锈蚀率计算获得;h0为截面有效高度;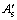 为受压钢筋截面面积;Es为钢筋弹性模量。
为受压钢筋截面面积;Es为钢筋弹性模量。
2.3 破坏阶段
此时锈蚀梁跨中截面极限弯矩Mu为
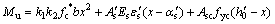 (22)
(22)
其中:
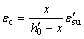 ≤0.003 3 (23)
≤0.003 3 (23)
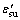 为锈蚀钢筋的极限应变,按式(2)计算;
为锈蚀钢筋的极限应变,按式(2)计算;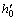 为破坏阶段的计算高度,主要考虑锈蚀钢筋引起的截面几何损失,等于截面有效计算高度h0减去保护层厚度。
为破坏阶段的计算高度,主要考虑锈蚀钢筋引起的截面几何损失,等于截面有效计算高度h0减去保护层厚度。
需要指出的是,绝大多数试验研究给出的钢筋锈蚀率为质量锈损率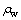 ,而理论分析时通常采用截面锈损率
,而理论分析时通常采用截面锈损率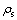 ,文献[18]给出二者间的换算关系如下:
,文献[18]给出二者间的换算关系如下:
 (24)
(24)
根据建议分析方法,对39根锈蚀钢筋混凝土梁的受弯承载力[2, 7, 16, 19-21]进行理论分析,得到的抗弯强度计算值与试验值的对比情况见表1。锈蚀钢筋混凝土梁受弯承载力试验值与理论值的比值随质量锈蚀率的变化情况如图5所示。
从表1可以看出:锈蚀梁受弯承载力试验值与计算值之比的平均值为1.100,方差为0.041,二者吻合较好,建议的抗弯强度计算方法可以用于锈蚀钢筋混凝土梁的受力分析。
表1 锈蚀钢筋混凝土梁抗弯强度计算结果与试验结果对比
Table 1 Comparison of flexural strength between test results and prediction results of corroded reinforced concrete beams
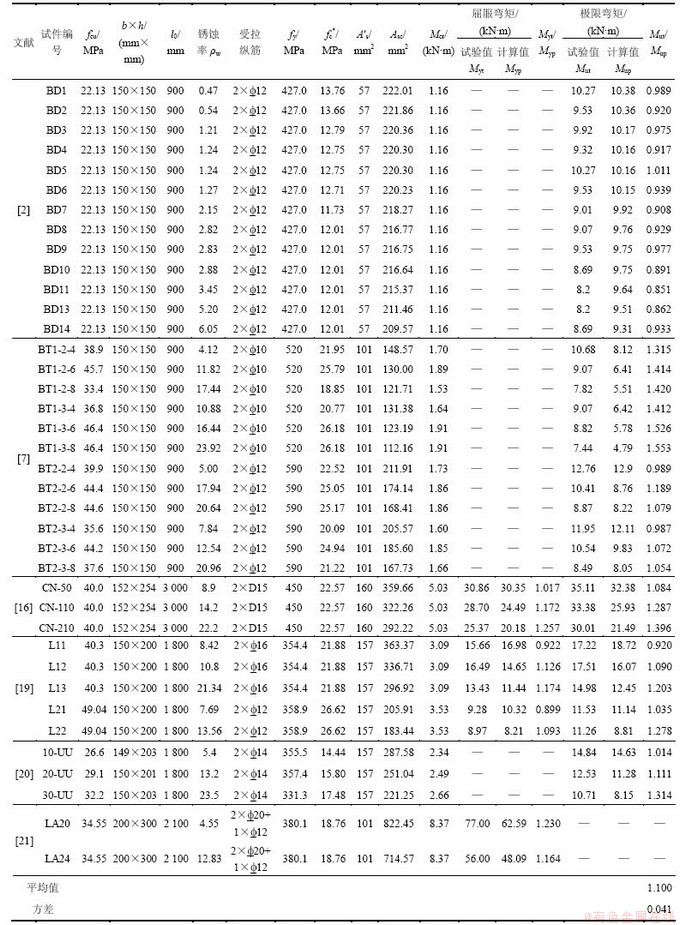
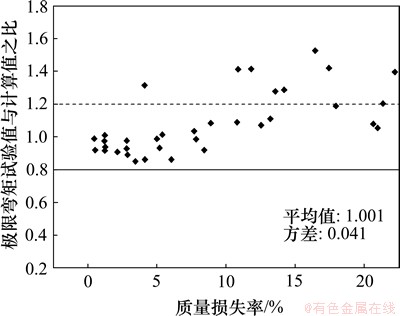
图5 极限弯矩试验值与计算值之比随质量锈蚀率的变化
Fig. 5 Ratios between test values and computation values of ultimate moment versus quality corrosion rates
从图5可以看出:随着质量锈蚀率的增大,理论预测值与试验值的偏差逐渐增大,个别试件二者的比值甚至大于1.2。原因可能在于质量锈蚀率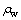 增大后,锈蚀钢筋的屈服平台缩短,锈蚀受弯构件由延性破坏向脆性破坏转变,本文假定的锈蚀梁受力三阶段中裂缝阶段将会很短,预期的受拉纵筋屈服将不会发生,此后随着荷载增加,锈蚀梁将很快达到极限弯矩而发生破坏,这些构件的破坏模式与假定的破坏模式已不完全相符。
增大后,锈蚀钢筋的屈服平台缩短,锈蚀受弯构件由延性破坏向脆性破坏转变,本文假定的锈蚀梁受力三阶段中裂缝阶段将会很短,预期的受拉纵筋屈服将不会发生,此后随着荷载增加,锈蚀梁将很快达到极限弯矩而发生破坏,这些构件的破坏模式与假定的破坏模式已不完全相符。
3 锈蚀钢筋混凝土梁的变形性能
钢筋混凝土简支梁在集中荷载作用下如图3所示。此时混凝土梁的跨中挠度△可按下式计算:
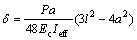 (25)
(25)
式中:P为作用外荷载;l为混凝土梁净跨,a为集中荷载作用点至支座处的距离;Ec为混凝土弹性模量;Ieff为混凝土梁的有效惯性矩。
对于锈蚀钢筋混凝土简支梁试件,钢筋锈蚀将造成混凝土和钢筋之间的黏结性能退化,跨中变形增大,理论分析时应予以考虑。此外,钢筋锈蚀发生的前提是混凝土碳化或氯离子侵蚀作用,此时混凝土在腐蚀环境下弹性模型也将发生轻微变化。因此,锈蚀受弯试件的有效惯性矩Ieff建议按下式计算:
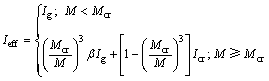 (26)
(26)
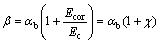 (27)
(27)
式中:Ieff为锈蚀梁的有效惯性矩;Ig为未开裂截面的惯性矩;Mcr为锈蚀梁开裂弯矩,按式(8)计算;M为锈蚀梁承受的弯矩;β为钢筋锈蚀造成的混凝土梁跨中挠度变化系数;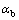 为钢筋锈蚀导致黏结性能退化所引起的挠度变化系数,偏保守地取图1中黏结应力下限值与峰值之比,若截面锈损率
为钢筋锈蚀导致黏结性能退化所引起的挠度变化系数,偏保守地取图1中黏结应力下限值与峰值之比,若截面锈损率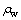 ≤5%,建议取0.4;若
≤5%,建议取0.4;若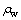 ≥15%,取0.15;锈蚀率为中间者线性插值取值;Ec为混凝土弹性模量,Ecor为受腐蚀混凝土的弹性模量,
≥15%,取0.15;锈蚀率为中间者线性插值取值;Ec为混凝土弹性模量,Ecor为受腐蚀混凝土的弹性模量,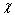 为二者之比,根据文献[22]建议按式(28)计算;Icr为跨中截面换算惯性矩,裂缝阶段锈蚀梁的换算惯性矩按式(29)计算;破坏阶段时,忽略锈蚀梁纵向受拉钢筋对截面刚度的贡献[23]按式(30)进行估算。
为二者之比,根据文献[22]建议按式(28)计算;Icr为跨中截面换算惯性矩,裂缝阶段锈蚀梁的换算惯性矩按式(29)计算;破坏阶段时,忽略锈蚀梁纵向受拉钢筋对截面刚度的贡献[23]按式(30)进行估算。
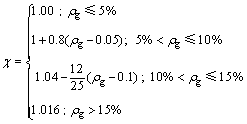 (28)
(28)
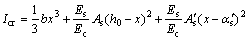 (29)
(29)
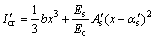 (30)
(30)
式中:Asc为锈蚀受拉钢筋的截面面积,可通过未锈钢筋截面面积乘以截面锈蚀率获得;h0为截面有效高度;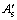 为受压钢筋截面面积;Es为钢筋弹性模量;x为锈蚀梁混凝土受压区高度,按式(17)计算。
为受压钢筋截面面积;Es为钢筋弹性模量;x为锈蚀梁混凝土受压区高度,按式(17)计算。
应用上述建议分析模型,对锈蚀钢筋混凝土矩形梁试件在集中荷载作用下抗弯性能进行了全过程理论计算。所有锈蚀梁跨中截面弯矩(或荷载)与跨中挠度曲线的计算结果与试验结果的对比情况如图6所示。
从图6可以看出:多数锈蚀试件按本文建议受弯分析模型计算得到的荷载-跨中挠度曲线与试验曲线吻合相对较好,变化趋势相当。但是,对于截面面积为150 mm×150 mm、跨度为900 mm的锈蚀钢筋混凝土梁(图6(a),6(b),6(g)和6(f))的计算曲线与试验曲线偏差较大,原因可能主要源于试件的尺寸效应。此外,所有锈蚀试件极限变形的计算结果与试验结果相差显著,理论计算获得跨中挠度较大,原因在于破坏阶段的跨中截面换算惯性矩Icr计算时,不宜忽略锈蚀梁纵向受拉钢筋对截面刚度的贡献,应乘以刚度折减系数来考虑锈蚀受拉钢筋在破坏阶段对截面刚度的贡献,此折减系数如何取值有待进一步研究。
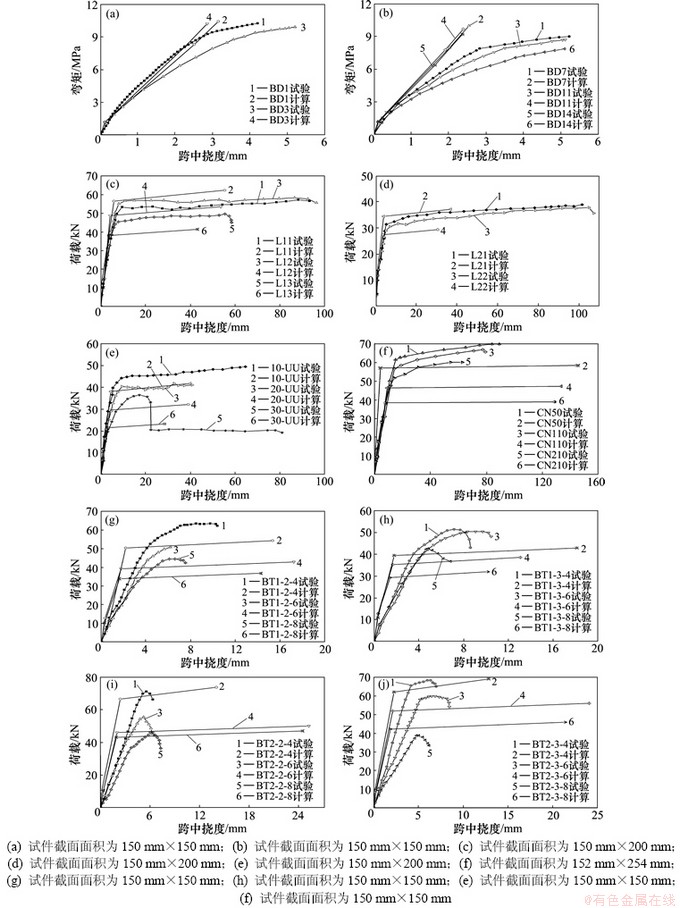
图6 计算曲线与试验曲线对比
Fig. 6 Comparison of test result and prediction results
4 结论
(1) 以锈损率较低的钢筋混凝土简支梁为对象,在平截面假定的基础上,提出了考虑钢筋、混凝土材料性能劣化和几何尺寸变化的受弯承载力计算公式。
(2) 锈蚀梁受弯承载力试验值与计算值之比的平均值为1.100,方差为0.041,吻合较好,抗弯强度分析方法可以用于锈蚀钢筋混凝土梁的受弯承载力计算。
(3) 多数锈蚀试件按本文建议受弯分析模型计算得到的荷载-跨中挠度曲线与试验曲线吻合相对较好,变化趋势相当。所有锈蚀试件极限变形的计算结果与试验结果相差显著,破坏阶段的跨中截面换算惯性矩Icr计算时应乘以刚度折减系数来考虑锈蚀受拉钢筋在破坏阶段对截面刚度的贡献。
参考文献:
[1] 牛荻涛. 混凝土结构耐久性与寿命预测[M]. 北京: 科学出版社, 2003: 95-126.
NIU Ditao. Durability and life forecast of reinforced concrete structure[M]. Beijing: Science Press, 2003: 95-126.
[2] 金伟良, 赵羽习. 锈蚀钢筋混凝土梁抗弯强度的试验研究[J]. 工业建筑, 2001, 31(5): 9-11.
JIN Weiliang, ZHAO Yuxi. Test study on bending strength of corroded reinforced concrete beams[J]. Industrial Construction, 2001, 31(5): 9-11.
[3] Rodriguez D J, Casal L M O. Load carrying capacity of concrete structures with corroded reinforcement[J]. Construction and Building Materials, 1997, 11(4): 239-248.
[4] Mangat P S, Elgarf M S. Flexural strength of concrete beams with corroding reinforcement[J]. ACI Structural Journal, 1999, 96(1): 149-158.
[5] Ballim Y, Reid J C. Reinforcement corrosion and the deflection of RC beams: An experimental critique of current test methods[J]. Cement & Concrete Composites, 2003, 25(6): 625-632.
[6] Malumbela G, Alexander M, Moyo P. Variation of steel loss and its effect on the ultimate flexural capacity of RC beams corroded and repaired under load[J]. Construction and Building Materials, 2011, 24(6): 1051-1059.
[7] Azad A K, Ahmad S, Azher S A. Residual strength of corrosion-damaged reinforced concrete beams[J]. ACI Materials Journal, 2007, 104(1): 40-47.
[8] 惠云玲, 李荣, 林志伸, 等. 混凝土基本构件钢筋锈蚀前后性能试验研究[J]. 工业建筑, 1997, 27(6): 14-18.
HUI Yunling, LI Rong, LIN Zhishen, et al. Experimental studies on the property before and after corrosion of rebars in basic concrete members[J]. Industrial Construction, 1997, 27(6): 14-18.
[9] 袁迎曙, 贾福萍, 蔡跃. 锈蚀钢筋混凝土梁的结构性能退化模型[J]. 土木工程学报, 2001, 34(3): 47-52.
YUAN Yingshu, JIA Fuping, CAI Yue. The structural behavior deterioration model for corroded reinforced concrete beams[J]. China Civil Engineering Journal, 2001, 34(3): 47-52.
[10] 牛荻涛, 卢梅, 王庆霖. 锈蚀钢筋混凝土梁正截面受弯承载力计算方法研究[J]. 建筑结构, 2002, 32(10): 14-17.
NIU Ditao, LU Mei, WANG Qinglin. Research on calculation method of the bending capacity of corrosive reinforced concrete beams[J]. Building Structures, 2002, 32(10): 14-17.
[11] 孙彬, 牛荻涛, 王应生. 锈蚀钢筋混凝土梁抗弯刚度评估方法研究[J]. 工业建筑, 2008, 38(2): 68-72.
SUN Bin, NIU Ditao, WANG Yingsheng. Study on evaluation method of flexural stiffness of corroded RC beams[J]. Industrial Construction, 2008, 38(2): 68-72.
[12] 王晓刚, 顾祥林, 张伟平. 碳纤维布加固锈蚀钢筋混凝土梁的抗弯刚度[J]. 建筑结构学报, 2009, 30(5): 169-176.
WANG Xiaogang, GU Xianglin, ZHANG Weiping. Flexural stiffness of corroded reinforced concrete beams strengthened with carbon fiber composite sheets[J]. Journal of Building Structures, 2009, 30(5): 169-176.
[13] Coronelli D, Gambarova P. Structural assessment of corroded reinforced concrete beams modeling guidelines[J]. Journal of the Structural Engineering, ASCE, 2004, 130(8): 1214-1224.
[14] Vecchio F J, Collins M P. The modified compression field theory for reinforced concrete elements subjected to shear[J]. ACI Structural Journal, 1986, 83(2): 219-231.
[15] Molina F J, Alonso C, Andrade C. Cover cracking as function of rebar corrosion Ⅱ: Numerical model[J]. Materials and Structures, 1993, 26(9): 532-548.
[16] El Maaddawy T, Soudki K, Topper T. Analytical model to predict nonlinear flexural behavior of corroded reinforced concrete beams[J]. ACI Structural Journal, 2005, 102(4): 550-559.
[17] Comité Euro-International du Béton(CEB). CEB-FIP model code-design code[S].
[18] 惠云玲, 林志伸, 李荣. 锈蚀钢筋性能试验研究分析[J]. 工业建筑, 1997, 27(6): 10-13.
HUI Yunling, LIN Zhishen, LI Rong. Experimental study and analysis on the property of corroded rebar[J]. Industrial Construction, 1997, 27(6): 10-13.
[19] 杨明. 锈蚀钢筋混凝土梁受弯性能研究[D]. 南京: 东南大学土木工程学院, 2006: 17-30.
YANG Ming. Study on flexural behavior of corroded reinforced concrete beams[D]. Nanjing: Southeast University. School of Civil Engineering, 2006: 17-30.
[20] 王晓刚. 碳纤维布加固锈蚀钢筋混凝土梁受弯性能研究[D]. 上海: 同济大学土木工程学院, 2008: 39-87.
WANG Xiaogang. Flexural behavior of corroded reinforced concrete beams strengthened with carbon fiber composite sheets[D]. Shanghai: Tongji University. School of Civil Engineering, 2008: 39-87.
[21] 李琛. 锈蚀钢筋混凝土梁承载力与刚度研究[D]. 长沙: 长沙理工大学土木与建筑学院, 2008: 11-19.
LI Chen. Research on strength and stiffness of corroded reinforced concrete beams[D]. Changsha: Changsha University of Science & Technology. School of Civil Engineering and Architecture, 2008: 11-19.
[22] 金祖权, 孙伟, 张云升, 等. 氯盐、硫酸盐作用下高性能混凝土损伤研究[J]. 工业建筑, 2005, 35(1): 5-7.
JIN Zuquan, SUN Wei, ZHANG Yunsheng, et al. Study on damage of HPC under the of corrosion of chloride and sulfate[J]. Industrial Construction, 2005, 35(1): 5-7.
[23] Toutanji H, Zhao L, Zhang Y. Flexural behavior of reinforced concrete beams externally strengthened with CFRP sheets bonded with an inorganic matrix[J]. Engineering Structures, 2006, 28(4): 557-566.
(编辑 杨幼平)
收稿日期:2012-10-16;修回日期:2013-01-28
基金项目:国家杰出青年科学基金资助项目(50725824);中国博士后科学基金资助项目(20110491651);陕西省自然科学基金资助项目(2013JQ7023);中央高校基本科研业务费专项资金资助项目(CHD2010JC082)
通信作者:邢国华(1983-),男,内蒙古呼和浩特人,博士,副教授,从事混凝土结构耐久性研究;电话:029-82337226;E-mail: guohuachd@yahoo.com