Sulfuric acid recovery from rare earth sulphate solutions by diffusion dialysis

TANG Jian-jun(唐建军)¹, ZHOU Kang-gen(周康根)², ZHANG Qi-xiu(张启修)²

1.School of Construction and Environmental Engineering, Shenzhen Polytechnic, Shenzhen 518055, China;

2. School of Metallurgical Science and Engineering, Central South University, Changsha 410083, China

Received 27 September 2005; accepted 22 December 2005

Abstract: Sulfuric acid recovery from rare earth sulphate solutions by diffusion dialysis was studied. The mass transfer model of diffusion dialysis was established, the comparison between the experimental results and mathematical results was carried out, and the numerical analysis on the effects of operational parameters was studied. The results indicate that the derived mathematical model shows good quantitative relation between sulphuric acid recovery ratio and operational parameters, and the mathematical results agree with the experimental results well. The numerical analysis results indicate that it is appropriate to keep the ratio of water and feed flow rates, processing capacity per membrane area and recovery ratio of sulphuric acid to be 1, 20 L/(m²?d) and 0.7-0.8, respectively.

Key words: diffusion dialysis; sulfuric acid; recovery; rare earth; mathematical model

1 Introduction

As an important industrial chemical, sulfuric acids are widely used in metallurgical and chemical processes, in which some waste solutions containing free sulfuric acids and metallic ions are therefore produced[1, 2]. If these waste acids can be recovered and reused in the production processes, a good closed-circuit will be created, and the economic and environmental effects are remarkable.

Traditional means to treat waste acids is to neutralize it with alkali. In addition, there are reports concerning its recovery by diffusion dialysis(DD)[3-5], electrodialysis[6,7], solvent extraction[8], and nanofiltra- tion[9,10], etc. DD has attracted much attention because of its simple and liable operation[11], but there are few reports about its mathematical model and numerical analysis of operational parameters up to now. Sulphuric acids recovery from rare earth(RE) sulphate solutions by DD and its integrated membrane technique with vacuum membrane distillation have been studied in our previous work[12,13]. The experimental results indicate that DD could separate sulphuric acid from RE sulphate solutions, and the integrated membrane technique could solve the problem of water balance in the process. The mathematical model of DD was further studied and the numerical analysis of the effects of operational parameters was also carried out in this paper.

The experimental apparatus of TSD—2 dialysis cell used in this study was made by TDKUYAMA Ltd, Japan. The membrane of DF120 was domestically made, the effective area of each membrane was 0.02 m², and there were 11 membranes in the membrane stacks. Two kinds of operations were carried out, i.e. one-pass operation and cycling operation. The solution flowing direction of one-pass operation is depicted in Fig.1. In cycling operation, the liquor flowing into raffinate tank and dialysate tank was led to feed tank and water tank respectively to make the solution cycle in the membrane stacks.

The experimental results in our previous work[12] indicated that RE concentration in dialysate was very low, and the volume change between feed solution and raffinate, water and dialysate was less than 2%. To simplify the following mathematical model, we consider the rejection ratio of RE is 100%, and the volume of feed and water have no change in the dialysis process.

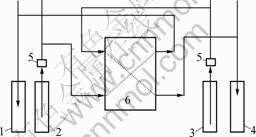
Fig.1 Experimental apparatus of TSD-2 dialysis cell:  1 Raffinate tank; 2 Feed tank; 3 Water tank; 4 Dialysate tank;  5 Pump; 6 Membrane stacks

3.1 Cycling operation

The volume and sulfuric acid concentration of feed are V₁ and c_1,i, those of dialyzate are V₂ and c_2,i, the mass transfer of sulfuric acid is m_t, the effective membrane area is A, the mass transfer coefficient is U₀, and the thickness of the membrane is d. The difference of sulfuric acid concentration between feed and dialyzate ?c_t at time t can be expressed as

            (1)

where  ?c_i=c_{1, i}-c_{2, i}.

According to Fick’s law:

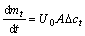
then

                (2)

According to Eqn.(2), the relationship between ln?c_t and t is linear, and the mass transfer coefficient U₀ can be achieved through the linear regression between them.

The cycling DD experiments at different tempera- tures were done. The RE and H₂SO₄ concentration in feed solution were 0.066 mol/L and 1.5 mol/L, respec- tively, the flow rates of feed and dialyzate were both 4.5 L/h. The experimental results are shown in Fig.2.

The mass transfer coefficients of sulphuric acid at different temperatures can be achieved from the regression of its corresponding experimental results shown in Fig.2, and are shown in Fig.3.

Fig.3 shows that a good linear relation between mass transfer coefficient and temperature can be achieved within the limited temperature range of 18-34℃, and their quantitative relation can be written as

U₀=2.139+0.070 4 θ   (10^{-5 m/min)}

      (18 ℃≤θ≤34 ℃)                     (3)

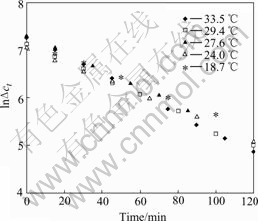
Fig.2 Relation of ln?c_t and time at different temperatures

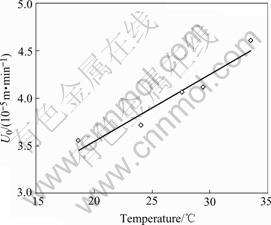
Fig.3 Relation of mass diffusive coefficient and temperature

3.2 One-pass operation

The material balance of one-pass DD process is shown in Fig.4[14,15], where marking Q, M and c reflect the flow rate, mass transfer and sulfuric acid concentration, subscript F, W and D reflect feed, water and dialyzate, and subscript i, f and x reflect initial, final and at any time, respectively.

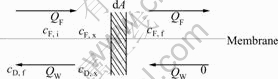
Fig.4 Schematic of material balance of one-pass DD

1) When the ratio of water and feed flow rates n= Q_W/Q_F=1,

c_{F, x}-c_{D, x}=c_{F, i}-c_{D, f}                            (4)

so

M=U₀(c_{F, i}-c_{D, f})A                             (5)

Since

M=Q_f(c_{f, i}-c_{F, f})=Q_Wc_D,f                        (6)

and defining sulfuric acid recovery ratio

                               (7)

then

                                (8)

2) When the ratio of water and feed flow rates n≠1, the rate equation of sulfuric acid diffusive transfer can be written as

dm=U₀(c_{F, x}-c_{D, x})dA                           (9)

and

(10)

then

                    (11)

Eqn.(8) and Eqn.(11) represent the quantitative relation between sulfuric acid recovery ratio and operational parameters. The sulfuric acid concentration in dialyzate c_D,f and that in raffinate c_F,f can be written as

                                (12)

c_F,f=(1-η)c_F,i                                 (13)

Eqn.(3), Eqn.(8) and Eqns.(11)-(13) represent the mass transfer model of DD.

Tables 1-3 show the comparison between the experimental results and mathematical results, which indicate that the mathematical results are satisfactory with experimental results, and the error is generally less than 7%.

Table 1 Effect of feed flow rate

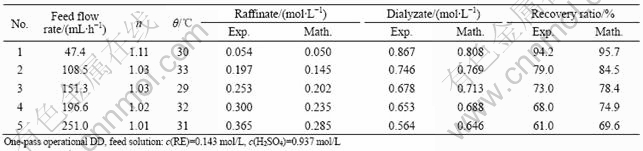
Table 2 Effect of ratio of water and feed flow rates

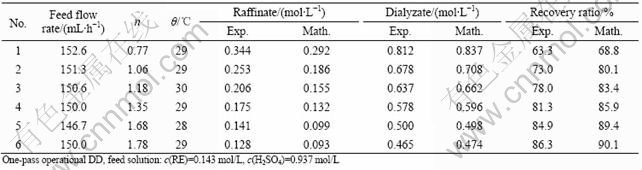
Table 3 Effect of different feed solutions

5 Numerical analysis

Firstly define the processing capacity per membrane area f, and the ratio of sulphuric acid concentration in dialyzate to that in feed solution R as:

                           (14)

                               (15)

Eqn.(14) can be further written as

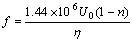   (n=1)               (16)

   (n≠1)               (17)

Fig.5 shows the numerical analysis of the relation between R and the ratio of water and feed flow rates. Under the condition of the same processing capacity per membrane area, i.e. the same feed flow rate, increasing the ratio of water and feed flow rates increases the sulphuric acid recovery ratio[12], but R decreases evidently, i.e. sulphuric acid concentration in dialyzate is diluted. It is apparently inconvenient for the reuse of the recovered low concentration of sulphuric acid.

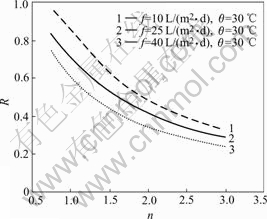
Fig.5 Relation between R and ratio of water and feed flow rates n

Fig.6 shows that increasing the ratio of water and feed flow rates increases the processing capacity per membrane area under the condition of the same recovery ratio, which is more evident when the ratio of water and feed flow rates is less than 1, but becomes flat when it is over 1. So it is appropriate to keep the ratio of water and feed flow rates to be 1 in the actual production process.

Fig.7 shows that increasing recovery ratio will decrease the processing capacity per membrane area rapidly. For n=1, controlling sulphuric acid recovery ratio to be 0.9, 0.8, 0.7 and 0.6, their corresponding processing capacity per membrane area are 5, 15, 26 and 40 L/(m²?d), respectively, i. e. when the recovery ratio decreases from 0.9 to 0.8, 0.8 to 0.7, and 0.7 to 0.6, the processing capacity per membrane area increases by

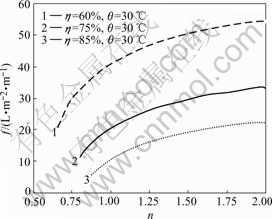
Fig.6 Relation of processing capacity per membrane area f and ratio of water and feed flow rates n

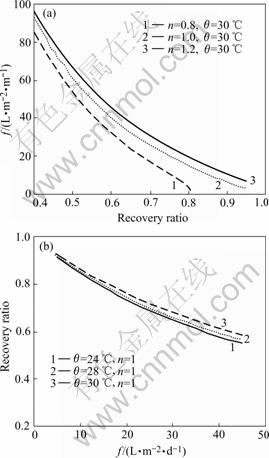
Fig.7 Relation of processing capacity per membrane area and recovery ratio

300%, 170% and 150%, respectively. Considering the contradictory relation between recovery ratio and processing capacity per membrane area, it is appropriate to keep the recovery ratio to be 0.7-0.8 according to the numerical analysis results, i.e. to keep the processing capacity per membrane area to be 20 L/(m²?d).

The mass transference model of dialysis diffusion was established, the comparison between experimental results and mathematical results was carried out, and the numerical analysis of the effects of operational parameters was studied. The mathematical results agree with the experimental results, and the numerical analysis results indicate that it is appropriate to keep the ratio of water and feed flow rates, processing capacity per membrane area and recovery ratio of sulphuric acid to be 1, 20 L/(m²?d) and 0.7-0.8, respectively.

[1] PEI Run. The Production of TiO₂ by Sulfuric Acid Route [M]. Beijing: Chemical Industry Press, 1982. (in Chinese)

[2] BODENBENNER K, PLESSEN H V, STERNER R. Regeneration of spent sulfuric acid [J]. Int Chem Eng, 1980, 20(3): 343-351.

[3] ZHANG Gui-qing, ZHANG Qi-xiu, ZHOU Kang-gen. Acid recovery from waste sulfuric acid by diffusion dialysis [J]. Journal of Central South University of Technology, 1999, 6(2): 103-106.

[4] SATOSHI Y, KAZUNORI I, SAKICHI G, KYOSHU H. Basic study on removal of sulfuric acid from process solution of zinc leaching residue by diffusion-dialysis [J]. Metallurgical Review of MMIJ, 1996, 13(1): 97-112.

[5] LIN S H, LO M C. Recovery of sulphuric acid from waste aluminum surface processing solution by diffusion dialysis [J]. Journal of Hazardous Materials, 1998, 60: 247-257.

[6] MARIO B, NANCY T, VIRGINIE G, AGNES C, GERALD P, ROGER S, CLAUDE G. Recovery of spent acid by electrodialysis in the zinc hydrometallurgy industry: performance study of different cation-exchange membranes [J]. Hydrometallurgy, 1997, 45(1/2): 137-160.

[7] LIU Heng, COVINGTON J. Acid recovery from synthetic Cu, Fe, Ni solution using electrodialysis [J]. Journal of Chengdu University of Science and Technology, 1994, 80(6): 73-79. (in Chinese)

[8] LI Qian, ZHANG Qi-xiu. Study on recovery of sulfuric acid from TiO₂ hydrolysis waste acid by solvent extraction [J]. Rare Metals and Cemented Carbides, 2003, 31(1): 4-7. (in Chinese)

[9] WAN Jin-bao. New disposition technology of waste acid liquor by nanofiltration [J]. Membrane Science and Technology, 2000, 20(3): 59-61.(in Chinese)

[10] BERNARD R, DENNIS G, MUELLER J J. Engineered membrane separation system for acid hydrometallurgical solution concentration, separation and treatment [A]. 4th International Conference COPPER- COBRE 99, Vol. 4 [C]. Pheonix, AZ, USA: Minerals, Metals and Materials Society, 1999. 567-580.

[11] SHI Jun, YUAN Quan, GAO Cong-jie. The Handbook of Membrane Technology [M]. Beijing: Chemical Industry Press, 1982. (in Chinese)

[12] TANG Jian-jun, CHEN Jian-jun, ZHOU Kang-gen, ZHANG Qi-xiu. Study on sulphuric acid recovery from RE sulphate solutions by diffusion dialysis [J]. Membrane Science and Technology, 2005, 25(2): 50-53. (in Chinese)

[13] TANG Jian-jun, ZHANG Wei, ZHOU Kang-gen, LI Rong-xian, ZHANG Qi-xiu. Sulphuric acid recovery from RE sulphate solutions by integrated membrane techniques [J]. Membrane Science and Technology, 2005, 25(3): 54-57. (in Chinese)

[14] JIANG Wei-jun, LEI Liang-heng, LIU Mao-lin. Chemical Principle [M]. Beijing: Tsinghua University Press, 1993. 20-23. (in Chinese)

[15] SHAO Gang. Water Treatment by Membrane Techniques [M]. Beijing: Metallurgical Industry Press, 2000: 16-18. (in Chinese)

(Edited by YUAN Sai-qian)

Corresponding author: TANG Jian-jun; Tel: +86-755-26731648; E-mail: tangjj7384@oa.szpt.net