组合连梁与墙肢节点恢复力模型试验研究
阎奇武1，唐莹莹2，陈康华1
(1. 中南大学 土木建筑学院，湖南 长沙，410075；
2. 长沙市代建工程建设指挥部，湖南 长沙，410008)
摘 要：为了建立平面内钢-混凝土组合梁与混凝土墙肢节点的恢复力模型，进行2个足尺平面内钢-混凝土组合连梁与混凝土墙肢节点的低周反复荷载试验，研究节点的破坏机理，得到节点的低周反复荷载作用下的滞回曲线。利用统计分析软件SPSS，采用对平面内钢-混凝土组合梁与混凝土墙肢节点滞回曲线的回归分析，考虑强度和刚度退化规律，建立平面内钢-混凝土组合梁与混凝土墙肢节点的恢复力模型。实验结果表明：平面内钢-混凝土组合梁与混凝土墙肢节点的低周反复荷载试验滞回曲线呈弓形，骨架曲线呈倒“Z”形，平面内钢-混凝土组合梁与混凝土墙肢节点有较好的延性和较强的耗能能力。
关键词：组合连梁；剪力墙；恢复力模型
中图分类号：TU398+.2 文献标识码：A 文章编号：1672-7207(2009)02-0504-08
Experimental study on restoring force models of composite coupling beam and pier joints
YAN Qi-wu1, TANG Ying-ying2, CHEN Kang-hua1
(1. School of Civil and Architectural Engineering, Central South University, Changsha 410075,China;
2. Headquarter of Changsha Daijian Construction Program, Changsha 410008, China)
Abstract: In order to found restoring force models of steel-concrete composite coupling beam and concrete pier (SCBCP) joints in plane, the experiments on 2 full-scale specimens of SCBCP joints were conducted under low reversed cyclic loading. By means of the experiments, failure patterns were researched, and hysteretic loops of the joints at the end of beams under low-reversed cyclic loading were acquired. According to the regressive analysis of hysteretic loops of SCBCP joints in plane through SPSS software of statistical analyzing, restoring force models of SCBCP joints in plane were established considering the strength and the stiffness degenerated rules. The experimental results show that hysteretic loops of SCBCP joints are in a bow pattern, and the outer diaphragms of the hysteretic loops of the joints are in a opposite “Z” pattern. As a result, energy dissipation and ductility of SCBCP joints at the end of beams under low reversed cyclic loading are better.
Key words: composite coupling beam; shear wall pier; restoring force models
震害和试验研究表明，建筑结构的倒塌，主要是由于结构构件的塑性变形能力小于所需要的能力，而基于承载力的设计并不能保证混凝土剪力墙达到预期的塑性变形或延性要求[1]。为增加混凝土联肢剪力墙的延性，我国大多把混凝土连梁设计成带水平缝或使用交叉钢筋的连梁，现行JGJ 3—2002规范则提出通过限制混凝土墙肢在重力荷载下的轴压比，降低混凝土连梁刚度，增设混凝土墙肢约束(或构造)边缘构件的方法来增加剪力墙的延性。徐培福等[2-3]在混凝土墙肢中增设型钢或钢板来增加剪力墙的延性。美国除了进行钢-混凝土组合整体剪力墙的研究[4]以外，近几年开展了带钢连梁双肢剪力墙的研究[5]，并在工程中得到了广泛应用，加拿大则开展了带钢-混凝土组合梁双肢剪力墙的研究[6]。剪力墙中连梁的内力较大[7]，降低混凝土连梁刚度可增大剪力墙的延性[8]，但刚度过小的混凝土连梁因承载力不足而过早被破坏，影响了剪力墙整体性能的发挥[9]。显然，剪力墙连梁既要求合适的承载力，又要求适当的刚度。可以说，钢-混凝土组合连梁比混凝土连梁更能胜任剪力墙连梁的要求。
历次震害结果表明，结构破坏部位大多发生在节点区，而节点破坏往往是导致整个结构倒塌的主要原因之一[10]。目前，人们对平面内组合连梁与混凝土墙肢节点的抗震性能研究较少，为此，本文作者对平面内组合连梁与混凝土墙肢节点的恢复力模型进行研究。
1 试验方案
试验以上海某框架(筒体结构)为背景，其平面图见图1。建筑层数为10层，抗震设防烈度为7度，Ⅲ类场地，抗震等级为：框架3级，剪力墙2级。该场地位于设计地震第1组内。
图1 典型框架-筒体结构平面布置
Fig.1 Typical plane of frame-core wall structure
取筒体-榀双肢剪力墙的墙肢与连梁的连接处节点为研究对象，主要研究连接节点区的受力性能。该批试验试件有2个：第1个试件编号为JD-3，按弱节点设计；第2个试件编号为JD-10，按强节点设计[11]。根据PKPM软件计算结果，将钢筋混凝土连梁设计成钢-混凝土组合连梁，截面尺寸见图2。根据GB 50017—2003规范，通过完全抗剪设计，抗剪连接件采用栓钉连接，其尺寸见图3。节点试件的主要参数见表1。
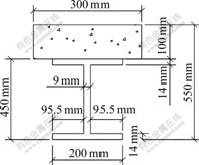
图2 组合梁截面尺寸
Fig.2 Size of section of composite coupling beam
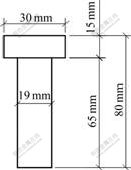
图3 栓钉尺寸
Fig.3 Size of fastener
表1 组合节点试件的主要参数
Table 1 Main parameters of composite joint samples
试件墙肢设置了约束边缘构件，约束区竖向钢筋采用双排布置，每排布置3根直径为16 mm即
的钢筋，横向箍筋配置
，墙肢非约束区竖向和水平钢筋均配置
，拉筋(箍筋)配置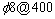
，墙肢混凝土保护层厚度取30 mm。组合梁混凝土板纵向钢筋配置
，横向钢筋配置
，组合梁混凝土保护层厚度取20 mm。混凝土采用商品混凝土，强度等级为C25。试件混凝土浇筑和养护按规范要求进行，在浇筑试件同时制作3个150 mm×150 mm×150 mm的混凝土立方体试块。
2个试件墙肢轴压力均由油压千斤顶施加，在实验过程中保持不变。为防止墙肢局部压力过大和使轴向荷载能够较均匀地分布于整个截面，在墙肢顶端设置加载分配梁。在加载过程中，墙肢保持垂直，墙肢下端通过螺栓固定在地槽内，墙肢上端通过水平长螺栓固定在反力墙上。JD-3连梁端竖向作用采用MTS电液伺服程控结构试验机施加低周反复作用，而JD-10连梁端竖向作用由于高度的限制采用千斤顶人工控制施加低周反复荷载。
节点试件在达到屈服荷载前采用荷载控制加 载，每级荷载反复1次，观察裂缝发展与节点区域钢筋、钢梁应变变化。当初步判断节点屈服时，采用变形控制加载，按屈服位移?y的倍数分级加载，每级各反复3次，当荷载下降到峰值的85%时，认为试件被破坏[12]。
2 试验结果
2.1 加载过程与破坏
2个组合试件从开始加载到破坏大致可分为3个受力阶段,即未开裂阶段、裂缝开展阶段和破坏阶段。这里，定义梁端向下加载为正向加载，梁端向上加载为反向加载。
2.1.1 试件JD-3加载过程与破坏特点
试验开始时，先在墙肢顶分级缓慢施加轴压力到预定值1.606 5 MN。轴压稳定后，梁端以每级荷载19 kN反复加载。在加载到95 kN时，连梁上出现第1条裂缝，试件进入开裂阶段。随着荷载的增加，梁上又出现少量裂缝，在190 kN卸载至零阶段，钢梁上翼缘2个应变片溢出，此时，梁端部位移达到7 mm。考虑到节点区钢梁可能发生屈服，此后改为位移控制加载，取加载屈服位移为7 mm。在加载屈服位移3倍的第1个循环峰值点243.8 kN时，节点核心区表面开始出现2条竖向裂缝，同时，节点区水平钢筋应变片的应变达到屈服值，由此推断节点被屈服，取屈服荷载为207 kN。在该循环的负峰值-249 kN时，墙肢上出现第1条横向裂缝，旧裂缝的宽度不断增加，墙肢上竖向裂缝宽度最大达0.22 mm。当荷载加到255 kN时，墙肢出现斜裂缝，旧裂缝不断扩展，宽度最大达0.54 mm。至最后1次加载，节点区横向裂缝宽度达3 mm，墙肢约束构件边缘处裂缝宽度达 6 mm，节点区被破坏。在整个试验过程中，组合梁混凝土表面仅有少量裂缝出现，且在墙肢混凝土表面出现裂缝后不再发展。
2.1.2 试件JD-10加载过程与破坏特点
先在墙肢顶分级缓慢施加轴压到预定值1.713 6 MN，待轴压稳定后，梁端以每级35 kN施加反复竖向荷载。在梁端竖向加载至173.8 kN时，连梁中部和根部均出现了裂缝。加载到208 kN时, 连梁出现新的裂缝，节点区钢梁应变片的应变可能达到屈服值，此后改用位移控制加载，取加载屈服位移为5 mm。当在加载屈服位移5倍的第1次循环峰值点233.5 kN时，节点区钢筋的应变片开始溢出，可判定此时节点已经屈服。当梁端竖向荷载达到-338 kN时，墙肢节点区开始出现裂缝，与该节点为强节点的设计相符合。最后1次加载，墙肢上不再出现新裂缝。最终连梁和墙肢连接处根部裂缝宽度达4 mm，明显可见钢梁屈曲破坏。在整个过程中，墙肢表面仅出现少许裂缝，宽度也较小，而组合梁上混凝土出现大量裂缝。主要试验数据结果见表2。
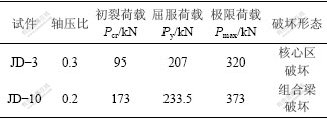
表2 组合节点主要试验结果
Table 2 Main test results of composite joints
2.2 组合节点梁端荷载-位移滞回曲线
2个组合节点的梁端荷载-位移滞回曲线见图4和图5。由2个节点滞回曲线可知：
a. 2个节点的滞回曲线表现出良好的耗能性能。
b. 在节点受力尚未超过屈服强度以前,加载和卸载均沿直线变化。
c. 节点的加载曲线斜率和卸载曲线斜率均随反复加载次数的增加而不断减小，但是，卸载曲线斜率减小幅度较加载曲线斜率减小幅度小，说明节点的卸载刚度退化现象不如加载刚度退化现象明显。
d. JD-3的滞回曲线捏缩现象比JD-10的滞回曲线捏缩现象明显，这是因为JD-3为弱节点，JD-10为强节点。
图4 试件JD-3梁端的荷载-位移滞回曲线
Fig.4 Hysteretic loops of load-displacement at the end of coupling beam of JD-3
图5 试件JD-10梁端的荷载-位移滞回曲线
Fig.5 Hysteretic loops of load-displacement at the end of coupling beam of JD-10
2.3 组合节点梁端滞回曲线的骨架曲线
节点滞回曲线峰值点的连线(外包线)即为骨架曲线，试验所得各节点的骨架曲线见图6。
(a) JD-3; (b) JD-10
图6 试件JD-3和JD-10的骨架曲线
Fig.6 Skeleton curves of samples of JD-3 and JD-10
3 恢复力模型
节点恢复力骨架模型采用三折线模型，在节点受力尚未超过屈服强度以前,加、卸载均呈直线变化， 加卸载模型采用直线模型，节点屈服后，反复加载时刚度、强度退化，加、卸载模型采用曲线模型。采用统计分析软件SPSS for Windows回归分析试验所得的滞回曲线及其骨架曲线试验数据，得到2个节点试件的骨架、加卸载模型特征。
3.1 骨架模型
骨架模型采用三折线模型，JD-3和JD-10各段的回归方程见表3和表4(其中，P为荷载，kN；
为位移，mm)，拟合骨架模型见图7。
表3 JD-3骨架曲线的回归方程
Table 3 Regressive equations of skeleton curve of JD-3
表4 JD-10骨架曲线的回归方程
Table 4 Regressive equations of skeleton curve of JD-10
(a) JD-3; (b) JD-10
▲—试验数据；── —回归曲线
图7 JD-3和JD-10骨架曲线模型
Fig.7 Models of skeleton curves of JD-3 and JD-10
3.2 刚度退化规律
节点屈服后刚度、强度退化，加卸载模型采用曲线模型。
3.2.1 正向卸载刚度
对JD-3，拟合方程为：
；
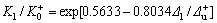对JD-10，拟合方程为：
。
其中：K1为正向加载刚度；
为正向加载初始刚度；
为正向卸载点位移；
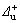为正向承载力位移。
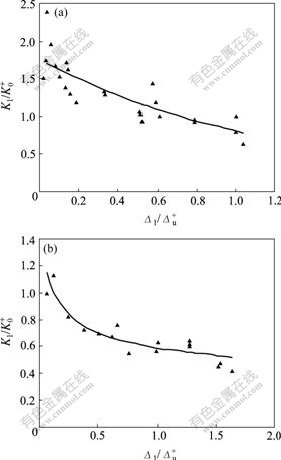
正向卸载刚度退化曲线见图8。
(a) JD-3; (b) JD-10
▲—试验值；── —拟合曲线
图8 正向卸载刚度的退化曲线
Fig.8 Degenerated curves of positive unloading stiffness
3.2.2 反向加载刚度
对JD-3，拟合方程为：
；
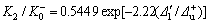对JD-10，拟合方程为：
。
其中：K2为反向加载刚度；
为反向加载初始刚度；
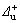为正向卸载时的残余变形；为正向承载力位移。
与
的关系曲线见图9。
(a) JD-3; (b) JD-10
▲—试验值；── —拟合曲线
图9 反向加载刚度的退化曲线
Fig.9 Degenerated curves of negative loading stiffness
3.2.3 反向卸载刚度
对JD-3，回归方程为：
；
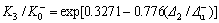对JD-10，回归方程为：
。
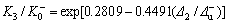其中：K3为反向卸载刚度；为反向加载初始刚度；
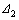为反向卸载位移；
为反向承载力位移。
回归曲线见图10。
(a) JD-3; (b) JD-10
▲—试验值；── —拟合曲线
图10 反向卸载刚度的退化曲线
Fig.10 Degenerated curves of negative unloading stiffness
3.2.4 正向加载刚度
对JD-3，拟合方程为：
；
对JD-10，拟合方程为：
。
其中：K4为正向加载刚度；为正向加载初始刚度；
为反向卸载时的残余变形；为反向承载力位移。
与
的关系曲线见图11。
(a) JD-3; (b) JD-10
▲—试验值；── —拟合曲线
图11 正向加载刚度的退化曲线
Fig.11 Degenerated curves of positive loading stiffness
3.3 恢复力模型
根据确定的骨架模型及刚度退化规律，可分别给出节点在循环荷载作用下的粱端竖向荷载-位移恢复力模型，见图12。
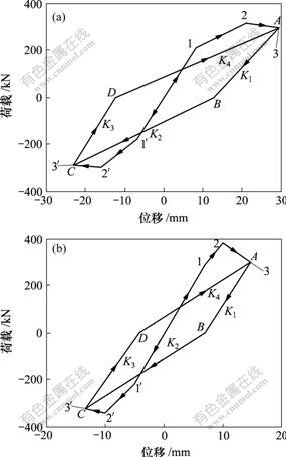
(a) JD-3; (b) JD-10
图12 JD-3和JD-10的恢复力模型
Fig.12 Restoring force models of JD-3 and JD-10
4 结果分析
a. 典型的荷载-位移滞回曲线有梭形、弓形和倒“S”形，“Z”形[13]。纯钢节点的滞回曲线呈典型的纺锤形，非常饱满，耗能大[14]。混凝土节点的滞回曲线有明显的捏缩现象，呈倒“S”形[15]，耗能比较小。由图4和图5可看出，组合节点的滞回曲线表现出良好的耗能性能，与纯钢节点和混凝土节点对比，其滞回曲线的饱和度介于两者之间，2个节点的滞回环中部略显捏拢特征。这主要是试验结束前节点区和组合梁处的裂缝已较宽，钢筋出现较大的滑移引起的。组合节点耗能能力明显强于混凝土节点耗能能力，而其刚度比混凝土节点的刚度低。
b. 由图6可见，2个节点的骨架曲线均呈倒“Z”形，说明节点在低周反复荷载下都经历了弹性、塑性的受力阶段，在达到最大荷载之后，梁端荷载下降比较少，这表明节点具有较好的延性。试件JD-3骨架曲线没有明显的拐点，由于试件JD-3按照弱节点设计，组合梁相对较强，故组合梁的屈服并不能表示节点的屈服。因此，判断屈服应从节点核心区的钢筋应变来判别。而由于JD-10为强节点，节点核心区屈服在组合梁的屈服或破坏以后。从JD-10的骨架曲线可以看出，与混凝土节点相比，混凝土墙肢与组合连梁节点的骨架曲线有着较长的下降段，变形能力较强。而与钢节点相比，由于钢材的延性较好，墙肢与组合连梁的骨架曲线相对变形能力较弱，因而，混凝土墙肢与组合连梁节点的延性介于混凝土节点与钢节点 之间。
c. 由图12可见，采用统计分析软件SPSS回归分析建立的2个试件恢复力模型呈弓形，上升段呈三折线，能反映节点的屈服、强度与刚度的退化。
5 结 论
a. 组合节点的滞回曲线呈弓形，明显好于混凝土节点的倒“S”型。
b. 2个节点的骨架曲线呈倒“Z”形，说明都经历了弹性和塑性受力阶段，有着较长的下降段，且下降幅度不大。
c. 建立的恢复力模型能反映节点恢复力试验曲线特征。
d. 钢-混凝土组合梁与墙肢节点具有较大的变形和良好的延性，耗能能力强。
e. 组合连梁与混凝土墙肢节点的抗震性能介于混凝土节点与钢节点之间，抗震性能良好。
参考文献：
[1] Park R, Paulay T. Reinforced concrete structures[M]. New York: A Wiley Interscience Publication, 1975.
[2] 徐培福, 薛彦涛, 肖从真. 带转换层型钢混凝土框架-核心筒结构模型拟静力试验对抗震设计的启示[J]. 土木工程学报, 2005, 38(9): 1-8.
XU Pei-fu, XUE Yan-tao, Xiao Cong-zhen. Seismic design concept from a pseudo-static test of steel-reinforced concrete frame-core wall structure model with transfer floor[J]. China Civil Engineering Journal, 2005, 38(9): 1-8.
[3] 王 敏, 曹万林, 张建伟. 组合剪力墙的抗震研究与发展[J]. 地震工程与工程振动, 2007, 27(5): 80-87.
WANG Min, CAO Wan-lin, ZHANG Jian-wei. Seismic research and development in composite shear walls[J]. Journal of Earthquake Engineering and Engineering Vibration, 2007, 27(5): 80-87.
[4] ZHAO Qiu-hong, Astaneh-Asl A. Cyclic behavior of traditional and innovative composite shear walls[J]. Journal of Structural Engineering, 2004, 130(2): 271-284.
[5] Hassan M, El-Tawil S. Inelastic dynamic behavior of hybrid coupled walls[J]. Journal of Structural Engineering, 2004, 130(2): 285-296.
[6] Gong B, Shahrooz B M. Steel-concrete composite coupling beams: Behavior and design[J]. Engineering Structures, 2001, 23(11): 1480-1490.
[7] 陆铁坚, 余志武, 蒋友良. 高层建筑筒体结构三维静力分析的改进条元法[J]. 中南大学学报: 自然科学报, 2004, 35(1): 133-137.
LU Tie-jian, YU Zhi-wu, JIANG You-liang. Improved finite strip method of three-dimensional static analysis of tall building framed tube and tube-in-tube structure[J]. Journal of Central South University: Science and Technology, 2004, 35(1): 133-137.
[8] 白国良, 楚留声, 李晓文. 高层框架-核心筒结构抗震防线问题研究[J]. 西安建筑科技大学学报: 自然科学版, 2007, 39(4): 445-450.
BAI Guo-liang, CHU Liu-sheng, LI Xiao-wen. The research on the problem of earthquake fortification line in high-rise frame-core wall structures[J]. Journal of Xi’an University of Architecture and Technology: Natural Science Edition, 2007, 39(4): 445-450.
[9] 徐培福, 戴国莹. 超限高层建筑结构基于性能抗震设计的研究[J]. 土木工程学报, 2005, 38(1): 1-10.
XU Pei-fu, DAI Guo-ying. Performance-based seismic design of tall building structures beyond the code-specification[J]. China Civil Engineering Journal, 2005, 38(1): 1-10.
[10] 贺国京, 阎奇武, 袁锦根. 工程结构弹塑性地震反应[M]. 北京: 中国铁道出版社, 2005.
HE Guo-jing, YAN Qi-wu, YUAN Jin-gen. Elastic-plastic seismic response of engineering structures[M]. Beijing: China Railway Press, 2005.
[11] 唐莹莹. 平面内钢-混凝土组合连梁与混凝土墙肢节点恢复力模型试验研究与分析[D]. 长沙: 中南大学土木建筑学院, 2007.
TANG Ying-ying. Experimental study and analysis on the restoring force model of composite coupling beam and pier joints in the plane[D]. Changsha: School of Civil and Architectural Engineering, Central South University, 2007.
[12] JGJ 101—96, 建筑抗震试验方法规程[S].
JGJ 101—96, Specification of testing methods for earthquake resistant building[S].
[13] 薛素铎, 赵 均, 高向宇. 建筑抗震设计[M]. 北京: 清华大学出版社, 2003.
XUE Su-duo, ZHAO Jun, GAO Xiang-yu. Seismic design of buildings[M]. Beijing: Tsinghua University Press, 2003.
[14] 梁柱节点专题组. 劲性钢筋混凝土梁柱节点性能及受剪承载力[C]//混凝土结构研究报告选集. 北京: 中国建筑工业出版社, 1994: 502-518.
Special Topic Group of Beam-column Joints. Behavior and shear strength of steel-reinforced concrete beam-column joints[C]// Selected Works of Concrete Structure Research. Beijing: China Architecture & Building Press, 1994: 502-518.
[15] 江见鲸, 李 杰, 金伟良. 高等混凝土结构理论[M]. 北京: 中国建筑工业出版社, 2007.
JIANG Jian-jing, LI Jie, JIN Wei-liang. Advanced theory of concrete structures[M]. Beijing: China Architecture & Building Press, 2007.
收稿日期：2008-10-27；修回日期：2008-12-28
基金项目：国家自然科学基金资助项目(50578161，50478092)；湖南省建设厅科技计划项目(2005-09)
通信作者： 阎奇武(1963-)，男，湖南长沙人，博士，副教授，从事混凝土结构的基本理论与高层建筑结构的抗震性能与设计研究；电话：13807486101；E-mail: yaqwu@mail.csu.edu.cn
