Multi-h CPM信号的低复杂度软判决算法
王鹏1,吴岭2,谷源涛1,梅顺良1
(1. 清华大学 电子工程系,微波与数字通信国家重点实验室,北京,100084;
2. 北京跟踪与通信技术研究所,北京,100094)
摘要:为提高带宽利用率与译码性能,提出一种Multi-h CPM信号的低复杂度软判决算法(LC-SOVA for MHPM),通过将判决符号处所汇聚的2条相位路径的累积度量值之差作为软判决值,以代替已有的二进制硬判决值。仿真结果表明:利用所提出的软判决值可以提高与信道编码级联后的抗误码性能,而不增加额外的计算复杂度。当信道编码采用码率为0.5的Turbo码,调制指数h分别为[8/13 9/13 10/13]与[2/4 3/4]时,误码率为10-5下的软判决编码增益分别可达0.7 dB与0.5 dB。在误码率为10-1的恶劣信道下均可获得约0.3 dB的编码增益。
关键词:Multi-h CPM;软判决;似然值;维特比算法;信道编码
中图分类号:TN92 文献标志码:A 文章编号:1672-7207(2013)12-4869-05
Low complexity soft-decision algorithm for Multi-h CPM
WANG Peng1, WU Ling2, GU Yuantao1, MEI Shunliang1
(1. State Key Laboratory on Microwave and Digital Communications,Department of Electronic Engineering, Tsinghua University, Beijing, 100084, China;
2. Beijing Institute of Tracking and Telecommunication Technology (BITTT), Beijing, 100094, China)
Abstract: In order to improve the bandwidth utilization efficiency and the decoding performance, a novel low complexity soft-output viterbi algorithm for Multi-h CPM (LC-SOVA for MHPM) is proposed to replace the traditional binary hard-output value with the soft-output value, which is the difference of the metric value of the two converging phase paths for the current symbol. Simulation results show that the proposed LC-SOVA can improve the BER performance and incur no extra complexity compared with the hard-decision algorithms. Specifically, when parameter h is [8/13 9/13 10/13] and [2/4 3/4] with Turbo code of rate 0.5, the performance gain for BER of 10-5 can be improved by 0.7 dB and 0.5 dB, respectively. LC-SOVA still has performance gain of 0.3 dB for BER of 10-1.
Key words: Multi-h CPM; soft-decision; likelihood; viterbi algorithm; channel coding
连续相位调制(continuous phase modulation,CPM)信号因其具有恒定的包络、较高的带宽利用率、受信道非线性影响小等优点而被广泛应用于各通信领域,如GSM蜂窝网络、蓝牙个人局域网、深空通信和遥测遥控等[1-3]。调制指数h是CPM信号的核心参数之一,它决定了CPM信号的功率谱与抗误码性能。传统的CPM使用单一的调制指数,因此又称为Single-h CPM,或连续相位频移键控(continuous phase frequency shift keying, CPFSK),目前对此类信号的研究已较充分[4-5]。近年来,在Single-h CPM的基础上,研究者们发现,使用多个周期变化的调制指数可以更充分地利用信号空间,从而获得更好的抗误码性能与更高的带宽利用率[6-7]。但与Single-h CPM相比,Multi-h CPM的调制与解调也更加复杂。近年来随着硬件性能的提高,Multi-h CPM的实用化成为可能。为了降低调制与解调的复杂度,研究者们提出可将相位调制转化为若干PAM信号的叠加[8-9],并使用Viterbi算法实现最大似然解调[10]。在一般解调过程 中,信号被处理成为二进制的硬判决值,期间损失了大量中间信息。Lin等[11]提出,如果能够利用解调过程中产生的各判决值的似然信息来辅助信道解码,则可以取得更好的抗误码性能。Hagenauer等[12]提出软判决Viterbi算法,并将其应用于卷积码的解码过程。随后,人们将软判决Viterbi算法应用于Single-h CPM信号的解调过程中[13],并在此基础上设计了一些低复杂度的软判决算法[14-15]。由于调制指数更加复杂,目前对低复杂度Multi-h CPM软判决算法的相关研究尚未见诸文献。本文设计了高斯加性白噪声下Multi-h CPM信号的低复杂度软判决算法(LC-SOVA for MHPM),它与传统硬判决算法有着相同量级的计算复杂度,但能够输出似然值信息以进一步提高与信道码级联后的抗误码性能。与码率为0.5的Turbo码级联后的仿真结果表明:使用软判决算法与信道编码级联可在误码率为10-5时获得0.5 dB以上的编码增益,并在误码率为10-1的恶劣信道下获得约0.3 dB的编码 增益。
1 Multi-h CPM信号的硬判决算法
Multi-h CPM的复基带表达式为 ,其中相位函数
,其中相位函数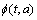 在第n个符号周期内满足
在第n个符号周期内满足
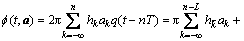
 (1)
(1)
式中:E为每个符号的能量;T为符号周期;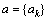 和h={hk}分别表示±1取值的发送符号序列和对应的调制指数序列。调制指数序列周期变化,其变化周期为K,令
和h={hk}分别表示±1取值的发送符号序列和对应的调制指数序列。调制指数序列周期变化,其变化周期为K,令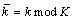 ,因此调制指数亦可简记为h={h1,h2,…,hK}。当K=1时,Multi-h CPM退化为CPFSK信号。q(t)为信号的相位响应波形,L为q(t)的持续符号周期数,当L=1时,q(t)为全响应信号,当L>1时为部分响应信号。
,因此调制指数亦可简记为h={h1,h2,…,hK}。当K=1时,Multi-h CPM退化为CPFSK信号。q(t)为信号的相位响应波形,L为q(t)的持续符号周期数,当L=1时,q(t)为全响应信号,当L>1时为部分响应信号。
全响应二进制Multi-h CPM信号是最常用的一类信号,其相位响应波形q(t)可表示为
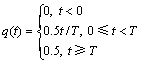 (2)
(2)
当调制指数h由有理数组成时,通分后它可以表示为h= 的形式,其中分子{p1,…,pK}和分母q均为正整数。相位函数
的形式,其中分子{p1,…,pK}和分母q均为正整数。相位函数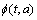 可以进一步地表示为:
可以进一步地表示为:
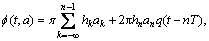
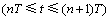 (3)
(3)
其中:右边第一项为累积相位,记为θn,满足
 (4)
(4)
右边第二项为瞬时相位,记为 ,满足
,满足
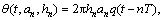
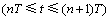 (5)
(5)
由于h为有理数,式(4)中的累积相位θn只能从集合 中取值,共计2q种累积相位状态。式(5)中瞬时相位
中取值,共计2q种累积相位状态。式(5)中瞬时相位 形状由发送符号an与其调制指数hn决定。式(3)中每个符号周期内相位函数的波形可由一个二元组
形状由发送符号an与其调制指数hn决定。式(3)中每个符号周期内相位函数的波形可由一个二元组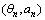 唯一确定,因此可能的波形数为4q。
唯一确定,因此可能的波形数为4q。
由于信号的累积相位状态有限,因此以时间作为横坐标,纵坐标为信号的相位除2π的余数,可得到Multi-h CPM的相位网格图。Multi-h CPM信号在每个符号周期内在不同状态间作1次跳转。
如图1所示,h=[2/4 3/4],故q=4。粗实线部分对应的序列为1,0,1,1,0,0,0,1,细实线对应为其他可能序列。
在高斯加性白噪声下,对于给定发送符号序列a,接收复基带信号r(t)的对数似然概率与如下累积度量成反比
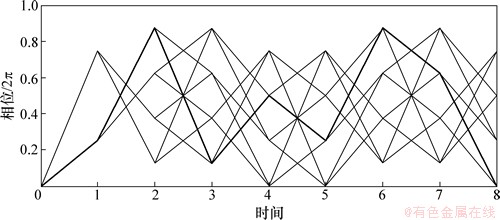
图1 Multi-h CPM的相位网格图(其中h=[2/4 3/4])
Fig. 1 Phase trellis graph for Multi-h CPM (h=[2/4 3/4])
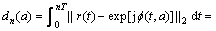
 (6)
(6)
其中:dn(a)表示到nT时刻为止,a对应的发送波形与接收信号r(t)在信号空间上的距离。最大似然解调符号序列 为能取得最小距离的发送符号序列,即
为能取得最小距离的发送符号序列,即
 (7)
(7)
穷举各种可能符号序列会导致复杂度随符号序列长度以指数关系增长,难以实际应用。使用维特比算法可以极大降低解调复杂度[12]。在不产生歧义的前提下,将传统维特比算法简称为硬判决算法。硬判决算法的复杂度与不同累计相位状态数2q成线性关系。
2 Multi-h CPM的软判决算法
2.1 似然值
硬判决算法输出±1取值的判决符号序列以参与信道译码。软判决算法能够利用判决过程产生的中间信息,进一步提高译码增益。输出的每个解调符号对应一个由似然值指示的软判决值,定义第n个符号的似然值为
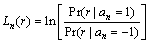 (8)
(8)
其中:r为收到的信号,an表示实际第n个发送符号,Ln(r)表示an的似然值,等于接收信号为r(t)时,发送符号分别取±1的概率之商的对数。当发送±1先验等概时,根据贝叶斯公式,似然值可以表达为
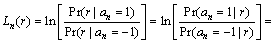
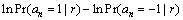 (9)
(9)
即似然值可表示为接收符号取±1的对数后验概率之差。
2.2 Multi-h CPM的软判决解调
当误码率低于信道译码门限时,最大似然解调序列的似然值远大于其他序列的似然值,噪声对似然值的影响较小。若最大似然解调序列对应的an=1,则an=1的出现概率约等于满足an=1的最大似然解调序列的出现概率,可表示为
 (10)
(10)
由于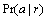 与相应的累积度量值dn(a)成反比,由式(10)可得
与相应的累积度量值dn(a)成反比,由式(10)可得
 (11)
(11)
同理,可将式(9)改写为:
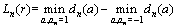 (12)
(12)
式(12)表示an的软判决值等于该处取+1与 1的度量之差。它可从硬判决Viterbi算法中求得,作为各个硬判决值对应的似然值。
1的度量之差。它可从硬判决Viterbi算法中求得,作为各个硬判决值对应的似然值。
基于以上讨论,提出了低复杂度的Multi-h CPM软判决算法(low complexity soft output viterbi algorithm for Multi-h CPM, LC-SOVA for MHPM),其算法流程如下所示。
1 FOR i=0 to 2q-1 DO
2 Di=0,ui1=ui2=…=uil=vi1=vi2=…=vil=0
3 ENDFOR
4 WHILE 传输未结束
5 更新hn,r(t)
6 FOR i=0 to 2q-1 DO
7 D*(i,1)=Di+
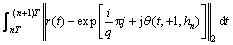
8 D*(i,-1)=Di+
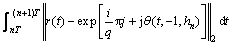
9 ENDFOR
10 FOR i=0 to 2q-1 DO
11 Da= ,
,
Db=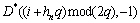
12 IF 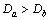
13 Di=Db, u*i={ub2, ub3, …, ubl, -1},
v*i={vb2, vb3, …, vbl, |Da-Db|}
14 ELSE
15 Di=Da, u*i={ua2, ua3, …, ual, 1},
v*i={va2, va3, …, val, |Da-Db|}
16 ENDIF
17 ENDFOR
18 FOR i=0 to q-1 DO
19 ui=u*i, vi=v*i
20 ENDFOR
21 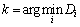 , aH=uk1, aS=
, aH=uk1, aS=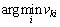
22 ENDWHILE
其中:Di为第i个累积相位状态对应的累积度量值;矢量ui和矢量vi分别为该累积相位状态对应的历史符号序列与似然值序列,其长度为l;输出值aH和aS分别为硬判决值(Hard)及其软判决似然值(Soft);k为最大似然序列对应的累积相位状态序号。算法共分2部分,从第1行至第3行为初始化过程;第4行至第22行为解调部分,这部分每接收到1个符号,将执行1次WHILE循环。下面详细介绍解调过程。
每符号周期内,首先将新接收到的信号r(t)与4q种可能的接收波形计算相关度量,并保留在2q×2的矩阵D*中。该过程对应于从第5行到第9行的循环。
随后,执行从第10行到第17行的循环,每个累积相位状态将根据接收信号的可能取值,跳转到新的累积相位状态。由于每个符号±1取值,因此在每个新的累积相位状态i上,将会有2条不同符号序列对应的相位路径汇合。选择具有较小累积度量值作为新的度量值Di。同时在矢量u*i中保留相应历史符号序列,在v*i中保留该序列对应的似然值,作为矢量ui和矢量vi的临时值。
最后,执行第18行到第21行,合并汇合的相位路径,并更新符号序列矢量ui和对应的似然值序列矢量vi。选取2q个累积相位状态中的最小累积度量值,用Dk表示。根据维特比算法,Dk亦为最大似然序列对应的度量值。把该状态对应的历史符号序列uk向前回溯的第l个符号uk1作为硬判决结果。同时把该状态对应历史似然值序列vk中的最小值作为似然值。
与硬判决算法相比,LC-SOVA增加了一倍的存储空间用于保存和历史状态对应的似然值,该似然值作为硬判决值的附加信息不参与判决过程,因此LC-SOVA可在保留中间信息以提高译码效率的同时,计算复杂度仍与硬判决算法相同,与累积相位状态数q成正比。值得注意的是;增加回溯长度l可以牺牲判决延时以降低解调误码率,但解调复杂度不受影响。当l足够大时(经验上可以取5q),解调误码率将不再随l增加而进一步降低。
3 仿真
仿真LC-SOVA在AWGN信道下的抗误码性能。使用生成多项式为G1=[1 1 1 1 1]与G2=[1 0 0 0 1]的Turbo码作为纠错码,码块大小为65 535,码率为0.5。为了评价软判决算法的抗误码性能,使用硬判决与信道码级联与直接硬判决作为参考算法,以h=[8/13 9/13 10/13]与h=[2/4 3/4] 2组调制指数为例进行了性能仿真,仿真结果如图2所示。
由图2可见:首先,使用信道编码可以显著提高抗误码性能。而与硬判决级联方案相比,使用软判决级联可获得0.5 dB左右的编码增益,表明其性能优于硬判决算法。其次,在误码率为0.1左右时,使用硬判决级联与直接硬判决的抗误码性能相差不大,2条误码曲线接近重合,而此时软判决级联仍可取得一定的编码增益。这表明:与硬判决级联相比,使用软判决级联可以在高误码率处仍获得编码增益,可适用于恶劣信道环境。虽然与硬判决算法相比,软判决算法具有更高的误码性能与更小的噪声门限,但两者的计算复杂度仍为同一数量级。
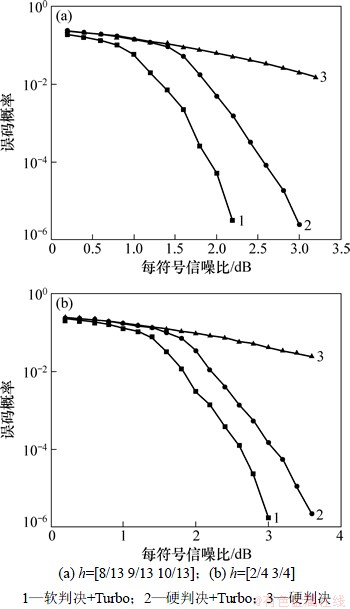
图2 Multi-h CPM软判决与信道编码级联的误码曲线(硬判决级联与直接硬判决为比较算法)
Fig. 2 BER performance for soft-decision with channel coding, hard-decision with channel coding and hard-decision without channel coding are simulated as comparison
4 结论
(1) 提出了Multi-h CPM信号的低复杂度软判决算法LC-SOVA,通过将判决符号处所汇聚的2条相位路径的累积度量值之差作为软判决值,以代替已有的二进制硬判决值。
(2) 硬判决方法值仅含有1比特信息,相比之下,软判决LC-SOVA算法因提取并保留了更多的信号信息,从而可用于提高与信道编码级联后的译码性能。软判决值作为硬判决值的附加信息不参与判决过程,因此,不会增加额外的计算复杂度。
(3) 当信道编码采用码率为0.5的Turbo码,调制指数h分别为[8/13 9/13 10/13]与[2/4 3/4]时,误码率为10-5下的软判决编码增益分别可达0.7 dB与0.5 dB。在误码率为10-1的恶劣信道下可获得约0.3 dB的编码增益。
(4) 所提出的软判决LC-SOVA算法适用于恶劣AWGN信道环境,可提高带宽利用率与译码效率。
参考文献:
[1] Park C, Womack B. Frequency domain processing for cyclic prefix-assisted multi-h CPM block transmission[C]//Proc IEEE MILCOM, Baltimore, USA: IEEE Press, 2011: 329-333.
[2] Saleem S, Stuber G. Trellis termination of multi-h CPM and the Diophantine frobenius problem[C]//Proc IEEE WCNC, Cancun. Mexico: IEEE Press, 2011: 1352-1357.
[3] Voglewede. Frequency hopping with multi-h CPM[C]//Proc IEEE MILCOM, Boston, USA: IEEE Press, 2003: 1089-1094.
[4] Barbieri A, Fertonani D, Colavolpe G. Spectrally-efficient continuous phase modulation[J]. IEEE Transactions on Wireless Communications, 2009, 8(3): 1564-1572.
[5] Anderson J, Aulin T, Sundberg C. Digital phase modulation[M]. New York: Plenum Press, 1986: 15-53.
[6] Geoghegan M. Description and performance results for a multi-h CPM telemetry waveform[C]//Proc IEEE MILCOM LA, USA: IEEE Press, 2000: 353-357.
[7] Cariolaro G, Erseghe T, Laurenti N, et. al. New results on the spectral analysis of Multi-h CPM signals[J]. IEEE Transactions on Communications, 2011, 59(7): 1893-1903.
[8] Perrins E, Rice M. PAM decomposition of M-ary Multi-h CPM[J]. IEEE Transactions on Communications, 2005, 53(12): 2065-2075.
[9] Yang R, Chern S. A generalized decomposition approach to multi-h continuous phase modulation[C]//Proc IEEE International Symposium on Information Theory, Yokohama, Japan: IEEE Press, 2003: 158-158.
[10] Perrins E, Rice M. Reduced-complexity detectors for multi-h CPM in aeronautical telemetry[J]. IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(1): 286-300.
[11] Lin S, Costello D. Error control coding 2nd edition[M]. New Jersey: Pearson Prentice Hall, 2004: 515-605.
[12] Hagenauer J, Offer E, Papke L. Iterative decoding of binary block and convolutional codes[J]. IEEE Transactions on Information Theory, 1996, 42(2): 429-445.
[13] Moqvist P, Aulin T. Serially concatenated continuous phase modulation with iterative decoding[J]. IEEE Transactions on Communications, 2001, 49(1): 1901-1915.
[14] Huang C, Ghrayeb A. A simple remedy for the exaggerated extrinsic information produced by the SOVA algorithm[J]. IEEE Transactions on Wireless Communications, 2006, 5(5): 996-1002.
[15] Barbieri A, Colavolpe G. Simplified soft-output detection of CPM signals over coherent and phase noise channels[J]. IEEE Transactions on Wireless Communications, 2007, 6(7): 2486-2496.
(编辑 何运斌)
收稿日期:2012-12-01;修回日期:2013-04-15
基金项目:国家自然科学基金资助项目(U0835003)
通信作者:谷源涛(1976-),男,河北保定人,副教授,博士生导师,从事无线通信和信号处理研究;电话:010-62783525;E-mail:gyt@tsinghua.edu.cn