DOI: 10.11817/j.issn.1672-7207.2016.03.035
块裂反倾巨厚层状岩质边坡变形破坏颗粒流模拟及稳定性分析
岑夺丰1,黄达1, 2,黄润秋3
(1. 重庆大学 土木工程学院,重庆,400045;
2. 重庆大学 煤矿灾害动力学与控制国家重点实验室,重庆,400044;
3. 成都理工大学 地质灾害防治与地质环境保护国家重点实验室,四川 成都,610059)
摘要:为了研究块裂反倾巨厚层状岩质边坡破坏机制及稳定性,基于PFC2D平行黏结模型和持续增加重力加速度方法,研究边坡破坏模式、应力-变形及能量耗散演化,并用临界重力加速度量化研究其稳定性。研究结果表明:边坡破坏模式主要有滑移、倾倒和溃屈破坏3类且随岩层倾角增大而逐渐转变;随岩块两相邻边长比l/h增大,边坡越倾向于发生倾倒破坏;滑移和倾倒破坏模式从坡脚向上坡体应力逐步达到峰值并峰后跌落,具有渐进破坏特征。而溃屈破坏模式坡体各部位应力呈“捆绑”型波动性塑性流动状态,具有大面积剧烈整体性破坏特征;随着岩层倾角(45°,60°,75°)增大,边坡临界重力加速度先减小再增大,稳定性在60°时最弱。边坡稳定性随岩块增大而增强,并主要受层间裂隙间距控制。
关键词:块裂反倾边坡;变形破坏;稳定性;演化;颗粒流
中图分类号:TU457 文献标志码:A 文章编号:1672-7207(2016)03-0984-10
Simulation of deformation and failure for blocky anti-dip thick-layered rock slopes using particle flow code and analysis on its stability
CEN Duofeng1, HUANG Da1, 2, HUANG Runqiu3
(1. School of Civil Engineering, Chongqing University, Chongqing 400045, China;
2. State Key Laboratory of Coal Mine Disaster Dynamics and Control,
Chongqing University, Chongqing 400044, China;
3. State Key Laboratory of Geohazard Prevention and Geoenvironment Protection,
Chengdu University of Technology, Chengdu 610059, China)
Abstract: In order to study the failure mechanism and stability for blocky anti-dip thick-layered rock slopes, based on the parallel bonded model of PFC2D and the method of increasing the gravitational acceleration, the slope failure mode, evolution of stress-deformation and energy dissipation were researched, and the stability was quantitatively analyzed according to the critical gravitational acceleration. The results show that the slopes show three failure modes, i.e. sliding, topping and bulking failure, which are transformational with the increase of dip angle of rock stratum. Topping failure is much more likely to happen with the increase of l/h, where l and h are the lengths of two adjacent sides of the rock blocks. The stress in slope gradually reaches the peak state and then drops from bottom to top for sliding and topping failure modes, which reflects the progressive failure characteristics. However, the stress in each part of the slope shows the bundle-like plastic flow state for bulking failure mode which has large area and dramatical integrity failure characteristics. The critical gravitational acceleration decreases first, then increases with the increase of dip angle of rock stratum (45°, 60°, 75°) and the stability is the weakest one when the dip angle of rock stratum is 60°. Slope stability increases with the increase of rock block size, and it is mainly controlled by spacing of interlaminar fractures.
Key words: blocky anti-dip slope; deformation and failure; stability; evolution; particle flow code (PFC)
反倾层状岩质斜/边坡破坏失稳诱发的灾难性事故常有发生,如加拿大Frank滑坡、美国Brilliant开挖边坡、秘鲁Ghurgar岩崩和我国的宜昌盐池河磷矿山体崩塌、华瑛山溪口镇滑坡、巴东黄腊石滑坡群等[1]。以往研究认为倾倒破坏是这类斜/边坡的主要失稳模式。M LLER[2]在分析Vaiont北麓滑坡成因时指出了岩块倾覆现象。ASHBY[3]推荐用“topping(倾倒)”一词来描述这类破坏,并开展了理论和试验研究。GOODMAN等[4]基于实例观察和试验研究,将倾倒破坏归纳为弯曲倾倒、块体倾倒和块体-弯曲倾倒3种基本类型,其中,弯曲倾倒常发生于岩层相对较薄(如片岩和板岩)的反倾层状斜/边坡,岩层类似悬臂梁而易发生弯曲断裂;块体倾倒常发生于含有层间裂隙的块裂反倾层状岩体,岩块在重力作用下具有转动矩而发生倾倒;块体-弯曲倾倒是前两者的结合,岩体既有弯曲断裂又有岩块转动。之后,学者们采用多种手段对反倾层状边坡破坏机制及稳定性进行了研究[5-11],如:BOBET等[5-7]克服了GOODMAN等[4]提出的倾倒稳定极限平衡计算方法的一些局限,如未将计算结果转换成易于工程应用的安全系数;GORICKI等[8]采用基底摩擦试验研究了反倾层状边坡和块裂反倾层状边坡的倾倒破坏,并用DDA进行了模拟;AYDAN等[9]采用基底摩擦试验和倾斜台面试验研究了块裂反倾层状边坡(包括层间裂隙贯通所有岩层和仅贯通层内2种情况)破坏模式(主要有滑移、倾倒及两者组合),并基于动态平衡方程建立了稳定性计算模型;ZHANG等[7]以龙滩水电站左岸进水口边坡为原型,用离心机模型试验模拟了其倾倒破坏问题,并在建立稳定性计算模型时考虑了层间裂隙连通率及岩块底面与侧面不正交的更一般情况;林杭等[10]用有限差分法尝试了层状边坡(包括顺层和反倾)变形破坏的模拟;BRIDEAU等[11]采用三维离散元方法模拟了倾倒破坏。客观地说,岩层厚度对边坡变形破坏具有明显影响,但以上研究并未对岩层尺度进行明确区分,而目前明确针对块裂状巨厚层状边坡的相关研究较少。近年来,基于离散元法的颗粒流程序(particle flow code,PFC)[12]因其在模拟岩石破裂、裂纹扩展和节理岩体变形破坏问题的独特优势而逐渐成为国内外岩石力学和岩体工程研究的热门工具[13-18]。PFC对细观离散颗粒元赋予简单的接触黏结模型,并以牛顿第二定律、力-位移定律以及黏结破坏判别准则来描述颗粒运动及其接触状态变化,在宏观上自然表现为材料(颗粒集合体)的变形和破坏,避免了宏观本构(包括岩石和结构面)的预先假设。鉴于物理模型试验存在的不足(如基底摩擦试验受模型尺寸限制,倾斜台面试验存在比尺效应方面的局限,离心机试验无法观察变形破坏演变过程)[7-9]及颗粒流方法的优势,本文作者采用平行黏结模型(parallel bonded model,PBM)的颗粒流模拟方法,考虑岩体结构参数如岩层倾角、层厚及层间裂隙间距的影响,研究典型块裂反倾巨厚层状岩质边坡变形破坏、应力状态及能量耗散演化机制,并对其稳定性进行评价。研究成果可为巨厚层反倾斜/边坡稳定性评价和加固设计提供参考。
LLER[2]在分析Vaiont北麓滑坡成因时指出了岩块倾覆现象。ASHBY[3]推荐用“topping(倾倒)”一词来描述这类破坏,并开展了理论和试验研究。GOODMAN等[4]基于实例观察和试验研究,将倾倒破坏归纳为弯曲倾倒、块体倾倒和块体-弯曲倾倒3种基本类型,其中,弯曲倾倒常发生于岩层相对较薄(如片岩和板岩)的反倾层状斜/边坡,岩层类似悬臂梁而易发生弯曲断裂;块体倾倒常发生于含有层间裂隙的块裂反倾层状岩体,岩块在重力作用下具有转动矩而发生倾倒;块体-弯曲倾倒是前两者的结合,岩体既有弯曲断裂又有岩块转动。之后,学者们采用多种手段对反倾层状边坡破坏机制及稳定性进行了研究[5-11],如:BOBET等[5-7]克服了GOODMAN等[4]提出的倾倒稳定极限平衡计算方法的一些局限,如未将计算结果转换成易于工程应用的安全系数;GORICKI等[8]采用基底摩擦试验研究了反倾层状边坡和块裂反倾层状边坡的倾倒破坏,并用DDA进行了模拟;AYDAN等[9]采用基底摩擦试验和倾斜台面试验研究了块裂反倾层状边坡(包括层间裂隙贯通所有岩层和仅贯通层内2种情况)破坏模式(主要有滑移、倾倒及两者组合),并基于动态平衡方程建立了稳定性计算模型;ZHANG等[7]以龙滩水电站左岸进水口边坡为原型,用离心机模型试验模拟了其倾倒破坏问题,并在建立稳定性计算模型时考虑了层间裂隙连通率及岩块底面与侧面不正交的更一般情况;林杭等[10]用有限差分法尝试了层状边坡(包括顺层和反倾)变形破坏的模拟;BRIDEAU等[11]采用三维离散元方法模拟了倾倒破坏。客观地说,岩层厚度对边坡变形破坏具有明显影响,但以上研究并未对岩层尺度进行明确区分,而目前明确针对块裂状巨厚层状边坡的相关研究较少。近年来,基于离散元法的颗粒流程序(particle flow code,PFC)[12]因其在模拟岩石破裂、裂纹扩展和节理岩体变形破坏问题的独特优势而逐渐成为国内外岩石力学和岩体工程研究的热门工具[13-18]。PFC对细观离散颗粒元赋予简单的接触黏结模型,并以牛顿第二定律、力-位移定律以及黏结破坏判别准则来描述颗粒运动及其接触状态变化,在宏观上自然表现为材料(颗粒集合体)的变形和破坏,避免了宏观本构(包括岩石和结构面)的预先假设。鉴于物理模型试验存在的不足(如基底摩擦试验受模型尺寸限制,倾斜台面试验存在比尺效应方面的局限,离心机试验无法观察变形破坏演变过程)[7-9]及颗粒流方法的优势,本文作者采用平行黏结模型(parallel bonded model,PBM)的颗粒流模拟方法,考虑岩体结构参数如岩层倾角、层厚及层间裂隙间距的影响,研究典型块裂反倾巨厚层状岩质边坡变形破坏、应力状态及能量耗散演化机制,并对其稳定性进行评价。研究成果可为巨厚层反倾斜/边坡稳定性评价和加固设计提供参考。
1 颗粒流模型建立
1.1 颗粒黏结模型及结构面生成
为模拟岩石类材料力学性能,POTYONDY等[13]提出了一种颗粒黏结模型(bonded-particle model,BPM)。PFC中颗粒黏结模型分为接触黏结模型(contact bond model,CBM)和平行黏结模型(parallel bond model,PBM) 2类[12]。其中,平行黏结模型具有抗拉伸、剪切和力矩效应及黏结破坏-材料宏观刚度劣化的特点,更适宜于岩石材料的模拟[13-18]。
在平行黏结模型中,可将颗粒接触和颗粒平行黏结分别等效为以颗粒A和B圆心为端点的弹性梁(见图1[13],梁长L为两颗粒半径R(A)和R(B)之和,即L=R(A)+R(B);t为梁厚,取1;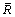 为平行黏结半径)。颗粒接触等效梁的法向、切向刚度kn和ks,弹性模量Ec和平行黏结等效梁的法向、切向刚度
为平行黏结半径)。颗粒接触等效梁的法向、切向刚度kn和ks,弹性模量Ec和平行黏结等效梁的法向、切向刚度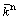 和
和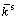 ,弹性模量
,弹性模量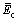 的计算式如下(其中,kn/ks和
的计算式如下(其中,kn/ks和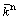 /
/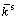 为预先取定的刚度比):
为预先取定的刚度比):
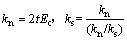 (1)
(1)
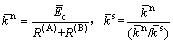 (2)
(2)
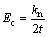 (3)
(3)
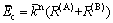 (4)
(4)
平行黏结弹性梁的强度条件为拉应力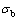 和剪应力
和剪应力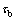 应分别控制在平行黏结法向强度
应分别控制在平行黏结法向强度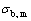 和平行黏结切向强度
和平行黏结切向强度 以内,即
以内,即
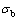 <
<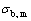 ,
,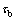 <
< (5)
(5)
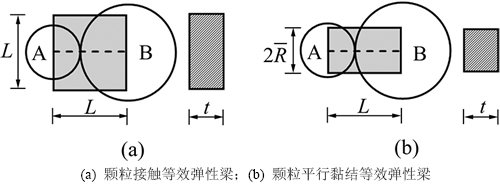
图1 平行黏结颗粒系统的等效弹性梁模型
Fig. 1 Equivalent elastic beam model of parallel bond particle system
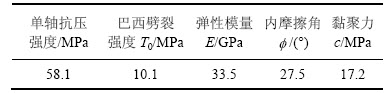
平行黏结模型涉及的微观参数见表1。可采用单(双)轴压缩、巴西劈裂等数值模拟试验来校核模型,通过与室内试验获得的常见岩石宏观参数(如单轴抗压强度、巴西劈裂强度、弹性模量、内摩擦角和黏聚力等)相匹配来标定微观参数[13-15],进而用于边坡稳定性分析。WANG等[15]用PFC2D平行黏结模型研究了节理连通率对岩体边坡稳定性的影响,CAMONES等[16-18]也引用或稍修改了WANG等[15]选用的微观参数研究了节理岩体边坡的稳定性,很好地模拟了变形破坏过程;岑夺丰等[17]模拟发现节理之间岩桥贯通模式与已有室内物理试验等研究结果具有较好的一致性,故文献[17]中微观参数(见表1)继续用于本文的模拟研究,其相应的宏观参数可通过数值试验获得,见表2。
本文采用文献[15-18]的结构面生成方法来设置岩层面和层间裂隙:将结构面两侧邻近颗粒间的黏结强度设置为0 MPa,即为平行黏结破坏。经数值直剪试验获得本次模拟的层面和层间裂隙宏观抗剪强度参数为:摩擦角20°,黏聚力0.4 kPa。
表1 岩石颗粒流模型微观参数
Table 1 Micro-parameters of PFC model for rock
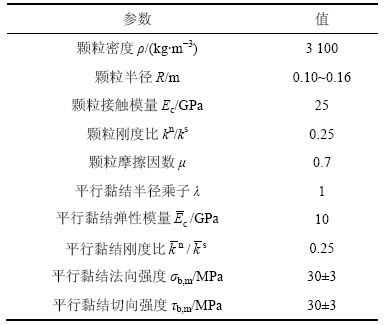
表2 模拟岩石宏观属性
Table 2 Macro-properties of simulated rock
1.2 模型设置
为方便研究,建立如图2所示坡角为70°的块裂反倾层状岩质边坡概化模型。首先建立总体高为32 m、宽为48 m的边界墙,采用粒径膨胀法生成指定粒径的颗粒并在无重力及近无摩擦状态下自动平衡以及消除浮点颗粒,从而生成均匀密实的初始颗粒集合体。然后,给所有颗粒设置重力加速度进行重力作用下的初始平衡,形成初始地应力。重力平衡稳定之后即可设置颗粒间的黏结形成岩石材料,并设置层面和层间裂隙(将结构面邻近颗粒标记为深色)。
岩层倾角α考虑45°,60°和75°共3种,岩层厚度h考虑2 m和3 m(根据GB 50021—2001“岩土工程勘察规范”[19],单层厚度大于1 m时为巨厚层),层间裂隙间距l考虑1,2和3 m,且层间裂隙均垂直于层面。故本文研究对象为具块状岩体结构的巨厚层状反倾边坡。比值l/h代表二维矩形岩块两相邻边长之比。在可能发生变形破坏的主要坡体处自下而上布置5个应力测量环(编号1~5)进行应力状态全过程监测。为促进坡体破坏失稳,仿照离心机试验原理,采用持续增加重力加速度的方法模拟加载。
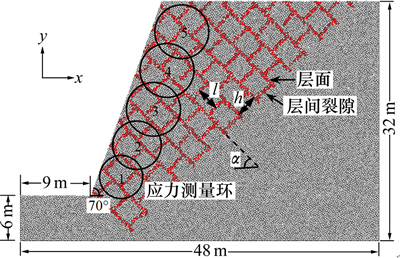
图2 边坡颗粒流模型
Fig. 2 PFC model of slope
2 破坏模式分析
对边坡破坏模式及其演变过程的明确认识是正确建立稳定性计算模型的前提,具有重要的工程意义。基于PFC2D模拟,主要根据岩块的运动特征及岩层整体的变形特征对边坡破坏模式进行研究。图3所示为块裂反倾巨厚层状岩体边坡的典型破坏模式(仅示意性给出了一些层间裂隙),即主要有滑移、倾倒和溃屈破坏3类。表3所示为所有模拟方案所观察到的块裂反倾巨厚层状边坡破坏模式。以岩层厚度h=2 m的模型为例阐述边坡变形破坏特征。图4所示边坡的破坏形态(图中标示了一些主要变形破坏差异特征),图5所示为3类破坏模式典型边坡的位移场特征。基于图3~5和表3,对3类破坏模式详细分析如下。
1) 滑移破坏模式。沿层间裂隙剪切滑移,在层间裂隙倾角相对较陡(即岩层倾角相对较缓)且间距较小(l/h较小)的情况下容易发生,如图4(a)所示。由于层间裂隙面摩擦角明显小于其倾角,当间距l较小时,相邻岩层岩块间嵌固段(层面)很短,互锁能力差,当坡脚最下面岩块失稳后,导致坡体沿裂隙面发生滑移。AYDAN等[9]开展的基底摩擦和倾斜台面物理试验也表明:当层间裂隙贯通所有岩层(即裂隙连通率为1)时也观察到了这类破坏模式。由图4(a)及其位移场图5(a)可见:该滑坡破坏区相对较浅,损伤区也较小。
2) 倾倒破坏模式。在岩层倾角较陡,尤其在l/h较大的情况下容易发生,是本文研究观察到最多的一类(岩层倾角α=60°时也一样),也是反倾边坡最常见的破坏模式。在重力作用下,岩层沿层面张裂并向坡外弯曲或倾倒变形,具体还可进一步分为2种亚类:一类是如图3(b)所示的曲线状弯曲倾倒,如图4(d)所示,层间裂隙间距相对较小,使岩层具有一定的柔性,可呈曲线状倾倒;另一类是如图3(c)所示的折线状翻转倾倒,典型的形态如图4(c)、图4(e)及图4(f)所示,层间裂隙间距较大,岩块重心落在层间裂隙以外,使其沿裂隙下端点发生转动,岩层呈折线状翻转倾倒,可在破裂带上发现较明显的弯折角。从图4可见:图4(b)所示边坡其实具有从滑移破坏模式到倾倒破坏模式过渡的特征,而图4(i)所示边坡具有从溃屈破坏模式到倾倒破坏模式过渡的特征,将这2类均归为倾倒破坏模式。由图4(f)及其位移场图5(b)可见:该滑坡破坏区相比图5(a)所示边坡(滑移破坏模式)较大,损伤区相近,而相比图5(c)所示边坡(溃屈破坏模式)破坏和损伤区均较小。
3) 溃屈破坏模式。在岩层倾角很陡(本文75°)、l/h不太大的情况下易发生,如图4(g)与图4(h)所示。与倾倒破坏单向弯曲且向外折断不同,由于岩层陡立,特别是坡体中下部岩层在重力作用下易发生S形屈曲,表现为鼓出且向内折断,进而导致坡体上部滑移或倾倒破坏。此处引用“溃屈”[20]这一术语主要是突出坡体中下部鼓出破坏-上部坡体坐塌的这一特征。由图4(h)及其位移场图5(c)可见:该滑坡破坏区及损伤区相比图5(a)所示边坡(滑移破坏模式)和图5(b)所示边坡(倾倒破坏模式)均较大,并且坡体下部破坏区较深,ZHANG等[7]在离心机模型试验中也发现了坡体下部较深部破裂的现象。
上述分析中的破坏区是根据边坡变形及破裂特征综合确定:边坡岩块沿层间裂隙及层面明显拉张或剪切破裂,且具有较大变形甚至运动特征的区域划分为破坏区;层面或层间裂隙存在一定的拉张或剪切损伤甚至破裂,但岩块总体变形相对较小且没有明显运动迹象的区域划分为损伤区。
表3 边坡破坏模式
Table 3 Slope failure modes
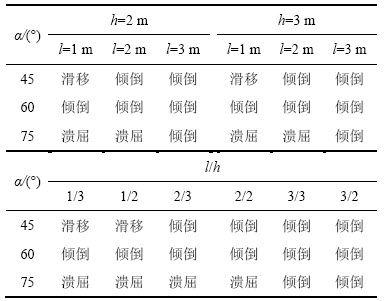
从表3可知:总体上,随岩层倾角增大,即层间裂隙倾角减小,边坡从滑移向倾倒破坏再向溃屈破坏模式转变。边坡破坏模式随岩块两相邻边长比l/h的变化规律也可得到。l/h作为岩块形状因素,综合反映了岩块长、宽影响。随l/h增大,边坡越易倾向于发生倾倒破坏。
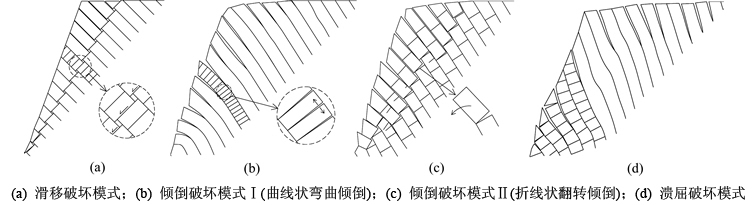
图3 边坡破坏模式示意图
Fig.3 Schematic diagrams of slope failure modes

图4 边坡破坏形态
Fig. 4 Slope failure modes
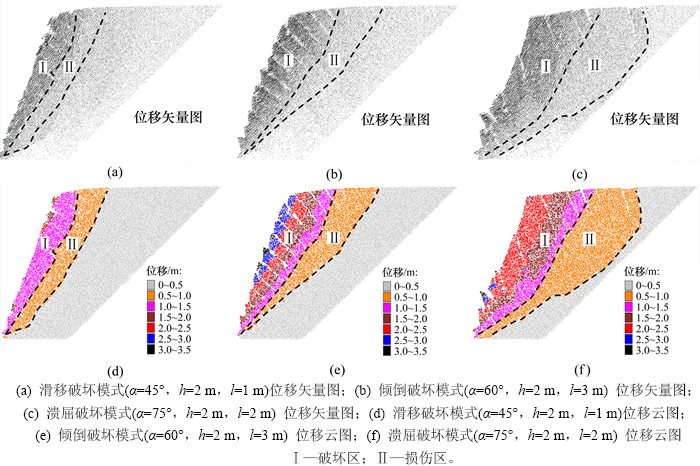
图5 3类破坏模式典型边坡位移场
Fig. 5 Displacement fields of typical slopes corresponding to three failure modes
3 坡体应力-变形及能量耗散演化
3.1 坡体应力计算
图2所示测量环所测应力为环内颗粒平均应力,可以考察较大范围内的整体应力变化,从宏观上更准确地把握坡体变形破坏动态信息。在x-y直角坐标系(见图2)下测量环内平均应力张量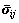 [12]为
[12]为
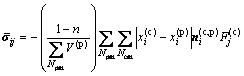 (6)
(6)
式中:Npm和Ncm分别为测量环内颗粒数和接触数;n为测量环内颗粒集合体孔隙度;V (p)为颗粒体积;xi(p)和xi(c)分别为颗粒中心和接触的位置;ni(c,p)为从颗粒中心指向颗粒接触的单位法向量;Fj(c)为颗粒接触和平行黏结产生的力。
3.2 坡体能量耗散计算
热力学定律表明,能量转化是物质物理变化过程的本质特征,物质破坏是能量驱动下的一种状态失稳现象。边坡破坏过程中的能量耗散主要用于结构面摩擦磨损及完整岩块的损伤破裂等,反映了破坏演化内在机制。
假设边坡系统是一个与外界没有热交换的封闭系统,并忽略岩块动能等本次模拟中相对很小的能量,则根据热力学第一定律可得出
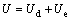 (7)
(7)
式中:U为边坡体力做功产生的总输入能量;Ud为边坡破坏过程中的耗散能;Ue为储存在坡体内的可释放弹性应变能。
本次模拟的总输入能量U由持续增长的颗粒体力在颗粒竖向位移方向作功产生,可通过下式获得:
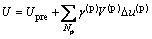 (8)
(8)
式中:Upre为到上一时步结束时的累积总输入能;γ(p)和△u(p)分别为当前时步内的颗粒重度和竖向位移;Np为模型颗粒数。
平行黏结模型颗粒集合体弹性应变能Ue包括颗粒应变能Uc和平行黏结应变能Upb 2部分,即
 (9)
(9)
其中:
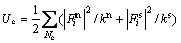 (10)
(10)
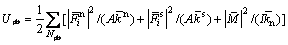 (11)
(11)
Nc和Npb分别为颗粒接触个数和平行黏结个数;i表示第i个接触或平行黏结; 和
和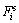 分别为法向和切向颗粒接触力;
分别为法向和切向颗粒接触力;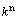 和
和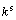 分别为各接触力对应的接触刚度;
分别为各接触力对应的接触刚度;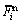 ,
,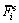 和
和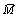 分别为法向平行黏结力、切向平行黏结力和平行黏结力矩;
分别为法向平行黏结力、切向平行黏结力和平行黏结力矩;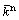 ,
,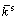 和
和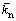 分别为各平行黏结力对应的刚度;A和I分别为平行黏结的横截面积和平行黏结的惯性矩。
分别为各平行黏结力对应的刚度;A和I分别为平行黏结的横截面积和平行黏结的惯性矩。
将式(10)和式(11)代入式(9),再将式(9)和式(8)代入式(7)即可求得耗散能Ud。
3.3 坡体应力-变形及能量耗散演化
图6~8所示为3类破坏模式典型边坡变形破坏过程中坡体竖向应力及能量耗散演化(图中曲线1~5分别为与测量环1~5对应的坡体各部位应力变化;1g=9.8 m/s2),现对演化特征分析如下。
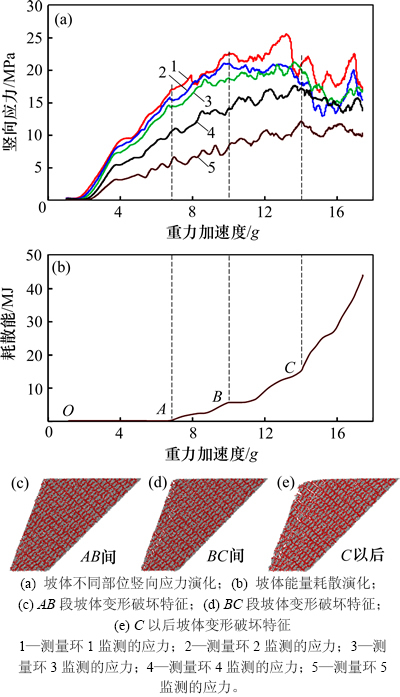
图6 典型滑移破坏模式边坡(α=45°,h=2 m,l=1 m)变形破坏过程应力及能量耗散演化
Fig. 6 Evolution of stress and energy dissipation in response to deformation and failure process of typical slope (α=45°, h=2 m, l=1 m) corresponding to sliding failure modes

图7 典型倾倒破坏模式边坡(α=60°,h=2 m,l=3 m)变形破坏过程应力及能量耗散演化
Fig. 7 Evolution of stress and energy dissipation in response to deformation and failure process of typical slope (α=60°, h=2 m, l=3 m) corresponding to topping failure modes
1) 能量耗散开始之后(图6~8中A点之后),各边坡竖向应力曲线具有明显的波动特征,且能量耗散随损伤破坏发展具有快慢交替但总体越来越快的特征,反映了坡体变形破坏发展的渐进性累积耗能机制。
2) 总体上看,除坡顶测量环5所测应力外,图6所示滑移破坏模式和图7所示倾倒破坏模式坡体应力具有峰后跌落的特征(其中后者应力跌落更明显),并大致从坡体下部到上部先后进入峰值和跌落,表明破坏具有渐进的特征;而图8所示溃屈破坏模式峰后应力并不明显跌落,而是呈波动性塑性流动状态,而且其中下部(测量环1~4)应力曲线几乎“捆绑”在一起,表明此破坏具有整体性,由图5(c)也可见其破坏和损伤区面积最大。当坡脚岩块鼓出破坏后,其上部坡体整体向下溃滑并使中下部呈压密状(1~4号曲线较靠近,即中下部应力相对较均匀,分异较不明显)。
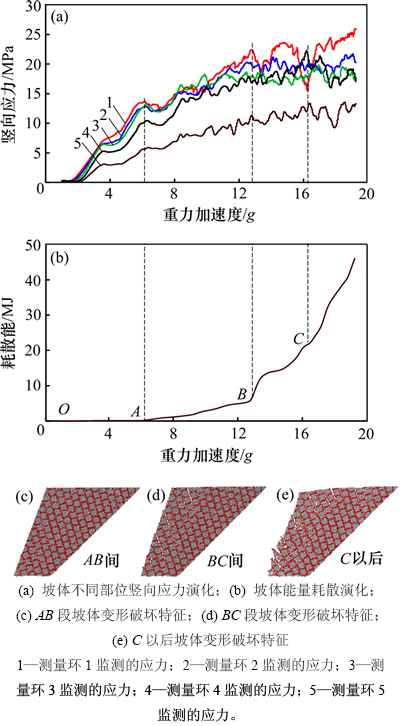
图8 典型溃屈破坏模式边坡(α=75°,h=2 m,l=2 m)变形破坏过程应力及能量耗散演化
Fig. 8 Evolution of stress and energy dissipation in response to deformation and failure process of typical slope (α=75°,
h=2 m, l=2 m) corresponding to bulking failure modes
3) 能量耗散大致在重力加速度为6g~7g之间时开始增加。在AB段,图6所示滑移破坏模式和图8所示溃屈破坏模式能量耗散增长较快,而图7所示倾倒破坏模式增长缓慢,表明倾倒破坏模式前期损伤破裂较小。而之后的BC段,图8所示溃屈破坏模式较其他2种模式能量耗散增长明显较快,表明破坏最剧烈。
4) AC段为开始耗能经坡体各部位应力调整先后达到峰值时(至最上部应力达峰值时为止),为主要损伤破坏发展阶段。该阶段重力加速度增量随滑移、倾倒、溃屈破坏模式依次增加,包括前期AB段也有同样规律,表明图6~8所示的这3类破坏模式的边坡对外力加载敏感性依次减弱。
5) 根据坡体应力及能量耗散演化特征,边坡变形破坏大体可分为几个阶段:a) 弹性变形阶段(OA段),该阶段坡体主要为弹性变形,尚无破坏发生,能量耗散基本为0 J;b) 破坏稳定发展阶段(AB段),该阶段坡体开始发生稳定破坏,能量耗散逐渐缓慢增加;c) 破坏不稳定发展阶段(BC段),该阶段大致从坡体下部应力到达峰值至坡体最上部应力进入峰值状态为止,各模式能量耗散开始较快增加,为主要破坏累积阶段,是进入完全破坏失稳的前兆;d) 完全破坏失稳阶段(C以后),该阶段坡体进一步完全破坏并失稳,能量耗散快速增加,可将该阶段起点C定义为临界失稳点。
4 稳定性分析
可用如图6~8中的边坡临界失稳点C所对应的临界重力加速度来比较边坡稳定性,临界重力加速度越大则边坡稳定性越好。表4所示为本次数值计算各边坡临界失稳时的重力加速度。由表4可知:
1) 随着岩层倾角为45°~75°,加速度先减小再增大,稳定性在60°时相对最差,75°时其次,45°时最好。文献[10]采用有限差分法研究无层间裂隙的反倾层状边坡时也表明,当岩层倾角为0°~90°时安全系数曲线呈现先增大、后减小、再增大的态势,其拐点分别位于20°和70°位置(70°时最小)。
2) 随着层间裂隙间距增大,临界重力加速度有显著增加;而随岩层厚度增加,临界重力加速度基本不变或略有增加。故总体而言,对于巨厚层状反倾边坡,稳定性随岩块增大而变好,并主要受层间裂隙间距控制。
3) 图9所示为临界重力加速度随l/h的变化规律。总体来看,临界重力加速度随l/h的增大而增大,其中岩层倾角为45°和75°时增长相对较快而60°时较慢,这又表明60°时边坡稳定性是相对最差的。另外发现,从l/h=1/2至l/h=2/3各曲线均有明显的跳跃(其中岩层倾角60°时跳跃相对较小),表明l/h较小时边坡稳定性相对较差。将图9中l/h=2/2时的临界重力加速度用l/h=3/3时的临界重力加速度替换,可知临界重力加速度整体上仍随l/h的增大而增大。从表4可知: 临界重力加速度在l/h=3/3时比l/h=2/2时的大,即在l/h相同情况下岩块越大,稳定性越好。
表4 临界重力加速度
Table 4 Critical gravitational accelerations

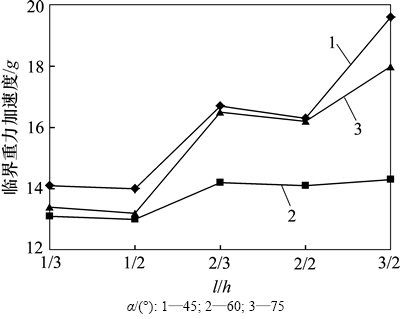
图9 临界重力加速度随岩块两相邻边长比l/h的变化
Fig. 9 l/h versus critical gravitational acceleration
另外,关于反倾层状边坡的稳定性计算虽然已有一些解析方法,但这些计算模型大多假设破坏面(滑动带)是破坏台阶逐个紧邻而成,整体呈一直线状(如图10(a))。然而,实际破坏面并不一定如此,而是呈几段破坏面连成的折线状,ZHANG等[7]开展的离心机模型试验表明了这一结果(如图10(b)),本文模拟结果也体现了这一点(见图5)。因此,为得到更可靠的稳定性计算结果,按可能的破坏滑动模式有针对性地建立计算模型是必要的。
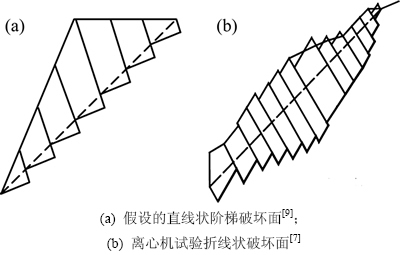
图10 反倾层状边坡破坏面形状
Fig. 10 Shapes of failure surface for anti-dip layered slopes
5 结论
1) 块裂反倾巨厚层状岩质边坡破坏模式主要有滑移破坏、倾倒破坏和溃屈破坏3类。总体上,随岩层倾角增大,边坡从滑移向倾倒破坏再向溃屈破坏模式转变。随岩块两相邻边长比l/h增大,边坡越倾向于发生倾倒破坏。边坡破坏区随滑移、倾倒、溃屈破坏模式依次增大。
2) 坡体各部位竖向应力变化具有波动特征,而能量耗散具有快慢交替且总体越来越快的特征。滑移破坏和倾倒破坏模式坡体各部位(从下至上)应力先后进入峰值并发生跌落,具有渐进破坏特征;而溃屈破坏模式坡体中下部竖向应力呈“捆绑”型波动性塑性流动状态,破坏具有整体性且最剧烈。
3) 随着岩层倾角从45°至75°变化,临界重力加速度先减小再增大,稳定性在60°时相对最差。总体上,稳定性随岩块增大而变强,并主要受层间裂隙间距控制。临界重力加速度总体随l/h的增大而增大,且从l/h=1/2至l/h=2/3有明显的跳跃,表明l/h较小时边坡稳定性相对较差。
参考文献:
[1] 谭儒蛟, 杨旭朝, 胡瑞林. 反倾岩体边坡变形机制与稳定性评价研究综述[J]. 岩土力学, 2009, 30(增2): 479-484, 523.
TAN Rujiao, YANG Xuzhao, HU Ruilin. Review of deformation mechanism and stability analysis of anti-dipped rock slopes[J]. Rock and Soil Mechanics, 2009, 30(Suppl 2): 479-484, 523.
[2] M LLER L. New considerations on the vaiont slide[J]. Rock Mechanics and Engineering Geology, 1968, 6(1): 1-91.
LLER L. New considerations on the vaiont slide[J]. Rock Mechanics and Engineering Geology, 1968, 6(1): 1-91.
[3] ASHBY J P. Sliding and toppling modes of failure in models and jointed rock slopes[D]. London: University of London. Imperial College, 1971: 10-130.
[4] GOODMAN R E, BRAY J W. Toppling of rock slopes[C]// Proceedings of the ASCE Specialty Conference on Rock Engineering for Foundations and Slopes. Colorado: Boulder, 1976: 201-234.
[5] BOBET A. Analytical solutions for toppling failure[J]. International Journal of Rock Mechanics and Mining Sciences, 1999, 36(7): 971-980.
[6] AMINI M, MAJDI A, VESHADI M A. Stability analysis of rock slopes against block-flexure toppling failure[J]. Rock Mechanics and Rock Engineering, 2012, 45(4): 519-532.
[7] ZHANG Jianhong, CHEN Zuyu, WANG Xiaogang. Centrifuge modeling of rock slopes susceptible to block toppling[J]. Rock Mechanics and Rock Engineering, 2007, 40(4): 363-382.
[8] GORICKI A, GOODMAN R E. Failure modes of rock slopes demonstrated with base friction and simple numerical models[J]. Felsbau, 2003, 21(2): 25-30.
[9] AYDAN  , SHIMIZU Y, ICHIKAWA Y. The effective failure modes and stability of slopes in rock mass with two discontinuity sets[J]. Rock Mechanics and Rock Engineering, 1989, 22(3): 163-188.
, SHIMIZU Y, ICHIKAWA Y. The effective failure modes and stability of slopes in rock mass with two discontinuity sets[J]. Rock Mechanics and Rock Engineering, 1989, 22(3): 163-188.
[10] 林杭, 曹平, 李江腾, 等. 层状岩质边坡破坏模式及稳定性的数值分析[J]. 岩土力学, 2010, 31(10): 3300-3304.
LIN Hang, CAO Ping, LI Jiangteng, et al. Numerical analysis of failure modes and stability of stratified rock slopes[J]. Rock and Soil Mechanics, 2010, 31(10): 3300-3304.
[11] BRIDEAU M A, STEAD D. Controls on block toppling using a three-dimensional distinct element approach[J]. Rock Mechanics and rock engineering, 2010, 43(3): 241-260.
[12] Itasca Consulting Group Inc. Manual of particle flow code in 2 dimension: theory and background[M]. 3.1st ed. Minneapolis: Itasca Consulting Group Inc, 2004: 1-4.
[13] POTYONDY D O, CUNDALL P A. A bonded-particle model for rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(8): 1329-1364.
[14] ZHANG X P, WONG L N Y. Crack initiation, propagation and coalescence in rock-like material containing two flaws: a numerical study based on bonded-particle model approach[J]. Rock Mechanics and Rock Engineering, 2013, 46(5): 1001-1021.
[15] WANG C, TANNANT D D, LILLY P A. Numerical analysis of the stability of heavily jointed rock slopes using PFC2D[J]. International Journal of Rock Mechanics and Mining Sciences, 2003, 40(3): 415-424.
[16] CAMONES L A M, VARGAS JR E A, DE FIGUEIREDO R P, et al. Application of the discrete element method for modeling of rock crack propagation and coalescence in the step-path failure mechanism[J]. Engineering Geology, 2013, 153(2): 80-94.
[17] 岑夺丰, 黄达, 黄润秋. 岩质边坡断续裂隙阶梯状滑移模式及稳定性计算[J]. 岩土工程学报, 2014, 36(4): 695-706.
CEN Duofeng, HUANG Da, HUANG Runqiu. Step-path failure mode and stability calculation of jointed rock slopes[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(4): 695-706.
[18] 贺续文, 刘忠, 廖彪, 等. 基于离散元法的节理岩体边坡稳定性分析[J]. 岩土力学, 2011, 32(7): 2199-2204.
HE Xuwen, LIU Zhong, LIAO Biao, et al. Stability analysis of jointed rock slopes based on discrete element method[J]. Rock and Soil Mechanics, 2011, 32(7): 2199-2204.
[19] GB 50021—2001, 岩土工程勘察规范[S].GB 50021—2001, Code for investigation of geotechnical engineering[S].
[20] 黄润秋. 汶川8.0级地震触发崩滑灾害机制及其地质力学模式[J]. 岩石力学与工程学报, 2009, 28(6): 1239-1249.
HUANG Runqiu. Mechanism and geomechanical modes of landslide hazards triggered by Wenchuan 8.0 earthquake[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(6): 1239-1249.
(编辑 刘锦伟)
收稿日期:2015-03-15;修回日期:2015-05-08
基金项目(Foundation item):国家自然科学基金资助项目(41472245, 41130745);重庆市研究生科研创新资助项目(CYB14018) (Projects(41472245, 41130745) supported by the National Natural Science Foundation of China; Project(CYB14018) supported by the Graduate Student Research Innovation of Chongqing)
通信作者:黄达,博士,教授,博士生导师,从事岩土工程和工程地质研究;E-mail:dahuang@cqu.edu.cn