基于颗粒流的平台圆盘巴西劈裂和岩石抗拉强度
孟京京,曹平,张科,谭鹏
(中南大学 资源与安全工程学院,湖南 长沙,410083)
摘要:使用颗粒流(PFC)虚拟实现不同中心角的平台圆盘巴西劈裂和直接拉伸试验,观察平台圆盘巴西劈裂中裂纹形成、扩展的一般过程,分析不同中心角对岩石破坏过程及破坏模式的影响。研究结果表明:平台中心角越大,岩石内损伤破坏程度越高,破坏模式变得更复杂。通过对不同平台中心角的圆盘试样断裂模式的观察和分析,并结合已有的研究成果推荐平台中心角为20°;利用直接拉伸数值试验的拉伸强度,计算出平台中心角为20°时的抗拉强度修正系数k=0.931 5。
关键词:岩石力学;数值试验;抗拉强度;平台中心角;颗粒流
中图分类号:TU458 文献标志码:A 文章编号:1672-7207(2013)06-2449-06
Brazil split test of flattened disk and rock tensile strength using particle flow code
MENG Jingjing, CAO Ping, ZHANG Ke, TAN Peng
(School of Resource and Safety Engineering, Central South University, Changsha 410083, China)
Abstract: A set of Brazil split tests of the flattened disk varied with central angles and the direct tension test were simulated by particle flow code (PFC). The common failure process in the rock specimen was found and the impact of different central angles of flats on rock specimens’ failure modes was analyzed. The result shows that as the central angle of flats increases, heavier damage degree is expested in the rock specimens and the failure mode becomes more complex. Based on the observation and analyses of rock specimens’ failure modes of different central angles, together with existed research results, central angle of flats is recommended to be 20°. When the central angle is 20°, tensile strength corrective factor, k=0.931 5, which is calculated with tensile strengths of direct tension test and Brazil split test of flattened disk.
Key words: rock mechanics; numerical test; tensile strength; central angle of flats; particle flow code
岩石的抗拉强度是岩石力学和工程的重要参数之一。目前,测定岩石抗拉强度的方法有:直接拉伸试验,巴西劈裂法,正方形板对轴压裂试验,对轴压模拉伸试验等[1]。由于巴西劈裂容易操作和对试样要求较低,所以通常采用巴西劈裂法测定岩石的抗拉强度。1978年,国际岩石力学学会(ISRM)推荐该方法为测定岩石抗拉强度的方法[2]。国内,各种岩石力学试验标准也推荐使用巴西劈裂法测定岩石抗拉强度[3-4]。按照规程要求,试验机对巴西圆盘施加径向荷载使其破坏。假定其为线性荷载,基于平面应力弹性方法进行求解,可得到圆盘各处的应力解析解[5]。从而,通过计算可得到岩石的抗拉强度。然而,这一经典的测试方法还有很多不足。事实上,巴西劈裂和直接拉伸所测的抗拉强度之间有较大的差别[1, 6-8]。进行巴西劈裂试验时,加载处会因为应力集中首先脆断,巴西劈裂的中心起裂条件不能得到保证[9-10]。为了改善加载处的应力集中现象,可以加工2个平台面作为加载面,这就是平台巴西劈裂试验。那么,就需要确定平台中心角的大小和抗拉强度计算式的修正系数。尤明庆等[11]利用ANSYS软件,结合格里菲斯强度准则对平台圆盘中心的受力状态和岩石抗拉强度进行了分析。喻勇勇[12]基于Mohr强度理论,提出了一个利用平台圆盘测试岩石抗拉强度的计算公式。尤明庆等[13]还通过试验得出抗拉强度随平台中心角2α增大的规律,并推荐平台中心角为20°~30°。于庆磊等[14]利用RFPA程序,观察并分析了平台中心角对试样破坏模式和应力分布的影响。已有的研究大都利用有限元方法和某种强度理论进行分析,然后确定平台中心角及建立抗拉强度计算公式。然而岩石材料自身的非均质、不确定性往往被忽略而且岩石内部破坏过程也没有被重视。本文作者基于颗粒流数值模拟程序建立了平台巴西劈裂试验的细观离散元模型,研究了劈裂过程中裂纹发展规律。通过对不同平台中心角下的巴西平台试验的分析,确定了合理的平台中心角的值和该平台角下岩石抗拉强度的计算式。
1 PFC岩石模型及试验过程
1.1 颗粒流模型
PFC作为一种离散元数值分析方法,通过分析圆形颗粒的运动及其相互作用来求解岩石力学问题[15]。使用BPM(黏结颗粒模型)时,模型内的颗粒随机生成,其粒径服从可以服从均匀分布或正态分布;通过内置的FISH函数,黏结模型的强度参数服从正态分布,从而模型具有一定的非均质性和随机性。这就能很好的表示岩土体的非均值性和参数的离散性。
PFC通过定义简单的颗粒接触模型,就可以表示材料复杂的破坏机制,避免了使用岩土体难以获得的本构关系。
1.1.1 接触本构模型
(1) 线性刚度模型。接触刚度模型提供了接触力和位移的弹性变化关系,可表示为:
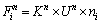 (1)
(1)
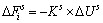 (2)
(2)
式中: 和
和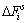 分别为法向和切向力;Kn和Ks分别是法向刚度,切向刚度;Un和△Us分别为法向重叠量和切向位移增量。
分别为法向和切向力;Kn和Ks分别是法向刚度,切向刚度;Un和△Us分别为法向重叠量和切向位移增量。
(2) 滑动模型。滑动模型通过定义摩擦系数得到最大摩擦力,在模拟中根据判断最大摩擦力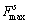 和静摩擦力
和静摩擦力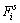 的大小关系来判断是否会滑动。最大摩擦力的计算公式如下:
的大小关系来判断是否会滑动。最大摩擦力的计算公式如下:
 (3)
(3)
式中:μ为摩擦因数。
(3) 平行黏结模型。PFC提供了2种基本的黏结模型:平行黏结模型和接触黏结模型。因为平行黏结模型可以很好的表示黏结断裂后,材料细观结构刚度的降低,所以对于岩石材料而言更为适合。平行黏结模型可以假想为胶结聚合物,颗粒在接触点处胶结在一起。同时黏结物自身受力时,允许产生一定的变形,当接触力超过黏结强度时,黏结破坏。
1.1.2 PFC计算过程
PFC是按照时步迭代算法不断计算,直至得到问题的解。计算过程的每一步包含2个基本部分(如图1所示)。每一计算步开始时,首先更新接触关系和实体(球和墙)位置的数据。然后对接触应用力和位移定律,从而得到实体间的接触力。接着,就可以根据已得到的接触力,应用牛顿第二定律决定每个颗粒的运动,如此不断循环。为了得到稳定,可靠的计算结果,计算时步必须足够的小。
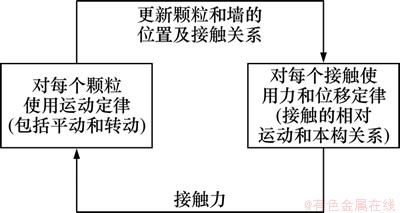
图1 PFC计算过程图
Fig. 1 Calculation cycle chart of PFC
1.2 PFC试验过程
1.2.1 基础模型建立
本次模型的建立可分为如下4步。
(1) 建立模型体。使用墙命令围成平台巴西圆盘,然后在其中生成随机分布、组合的球状颗粒集合体。最后,设置颗粒集合体接触关系细观参数。
(2) 通过半径扩大的方法得到颗粒集合体初始的各向同性应力条件。
(3) 去除漂浮粒子。球的配位数小于4的颗粒定义为漂浮粒子,并予去除。
(4) 设置平行黏结模型。这样平台巴西圆盘的岩石模型最终生成。
1.2.2 参数标定过程
PFC的输入变量并不是人们所熟悉的宏观参数,而必须经过多次标定后才能找到的细观参数。所以使用该数值方法时,首先要假定其输入参数,然后对模拟结果和真实材料的力学性质进行比较;不断调整输入参数,比较其结果,最终两者结果相一致的一组参数就是所需的模型参数。
本次标定过程使用了某矿山的大理岩试样,所取的宏观参数具有一定的代表性。标定过程选择了表1所示的宏观参数,进行了巴西劈裂和单轴压缩虚拟试验。标定过程后,颗粒半径在0.16~0.26 mm范围之间,模型主要微观参数如表2所示。
1.2.3 数值试验的设置
在圆盘的2个平台面上分别设置一个墙,设墙的速度为1×10-2 m/s (在物理试验中速度很大;但对于PFC来说,约4×10-10 m/步已经足够小[16])进行加载。为便于问题的研究,墙的摩擦因数设为0,即加载过程中墙与颗粒之间无摩擦作用。当某点黏结破坏时,FISH程序会在两球球心连线的法线方向上用一条线段标志破裂时所产生的裂纹。
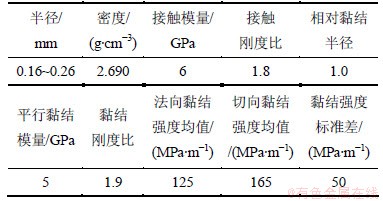
表1 岩石宏观参数
Table 1 Macro-properties of rock

表2 模型微观参数
Table 2 Micro-properties of rock in numerical simulation
2 实验结果分析
2.1 平台巴西圆盘受压破裂过程
本文通过观察不同平台中心角圆盘内裂纹的扩展过程,发现了岩石破坏的一般过程。图2所示为平台中心角为15°时,所做的平台巴西圆盘劈裂过程示意图。在图2中,黑色线段表示为裂纹。由于岩石内随机分布的缺陷,当其受力时,在微孔或微裂隙末端易造成应力集中,从而在低应力状态下岩石内部就会有微裂纹的产生和扩展[17]。所以,在加载的初始阶段,产生了随机分布的裂纹(如图2(a)和(b)所示),这和基于强度理论分析的结论相异。可以看到:端部应力集中效应依然存在,端部附近分布的裂纹较其他地方要集中。当平台中心角大于20°时,这种效应已不明显(如图3所示)。随着荷载的不断增加,裂纹的出现变得有序。裂纹集中出现在已有的裂纹周围并且裂纹之间相互搭接,沿径向不断扩展。最终,产生的裂纹沿径向贯通,试样破坏。

图2 平台巴西圆盘劈裂过程示意图
Fig. 2 Process of brazil split test of flattened disk
实际上,岩石的破裂过程是破坏单元从无序分布到集中有序的自组织过程[18]。在加载过程的初始阶段,荷载较小,产生于岩石内的裂纹带有很大的随机性。所以,本文并不赞同在岩石均匀性假设的前提下,通过强度理论来判断岩石这种特殊材料的断裂起始位置。根据尤明庆等[11, 19]的分析,平台中心角2α≥20°时,平台圆盘满足中心起裂的条件。然而在这种情况下,试样受压断裂时,初始的裂纹依然是随机分布,这一点是由具体一块岩石中随机分布的缺陷决定的。
随着荷载的增加,岩石的破裂过程逐渐变得有序。通过应力分析和强度理论,可以确定相对应力最大的位置在圆盘的受压直径上,也就是圆盘会对径劈裂为相等的2部分。试验结果表明:不断增加的裂纹沿着圆盘的受压直径,集中分布在已有的裂纹周围。随着裂纹的不断增加,裂纹之间不断相互作用逐渐贯通,最终形成一个破坏面。观察到的破坏的过程和理论上的分析还有一定的差异,其主要原因是岩石的非均质性以及破裂过程的非线性。

图3 中心角为20°的试件内分布的裂纹
Fig. 3 Cracks in specimen with central angle equaling 20°
2.2 平台中心角对裂纹扩展的影响
整个劈裂过程中,裂纹的扩展和应力变化具有很大的相关性(如图4所示)。在加载初始阶段应力较小,裂纹很少而且扩展缓慢。在临近破坏荷载时,裂纹发展迅速,弹性应变能迅速释放,驱动裂纹迅速扩展、贯通。峰值应力后产生的大量裂纹主要是断裂面拉开时的拉伸裂纹。这个阶段拉裂纹变化最为明显,试件由体积压缩转为扩容,随后宏观断裂面形成。
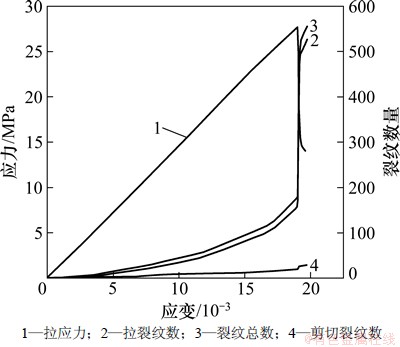
图4 平台巴西劈裂过程裂纹变化
Fig. 4 Cracks increase in process of brazil split test of flattened disk
平台中心角会影响到试件内的应力分布,进而对整个劈裂过程产生影响。如图5所示,平台中心角越大,劈裂试验过程中裂纹产生得越多、增长得越快,特别当平台中心角大于25°时,裂纹数量增加得更加迅速。裂纹数量随着应变增加而增加,可以作为岩石内损伤的演化和裂纹的扩展程度的表征。这意味着中心角越大,岩石损伤越大,破坏模式变得更加复杂。
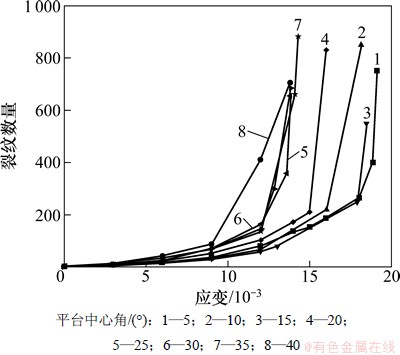
图5 不同平台中心角巴西劈裂过程裂纹数量的变化
Fig. 5 Number of cracks develops in the process of brazil split test of flats of different central angle
2.3 不同平台中心角的断裂模式
当平台中心角不大于20°时,可以看到巴西圆盘可以沿直径劈裂为两半。当平台中心角大于20°时,巴西盘的断面变得复杂,而且平台圆盘中心裂纹扩展方向和受力方向有一定的夹角(如图6所示)。随着平台中心角增大,拉应力降低,而压、拉应力比增大[11],圆盘破裂方式从单纯的拉断到应力组合的复杂断裂 方式。
当平台中心角等于26.7°时,这种组合破坏方式表现的更加明显[14]。所以,当平台中心角大于25°以后,试验测量所得到的名义抗拉强度能否反映岩石的抗拉性能值得怀疑。然而,平台中心角越大,端部的集中应力影响就越小和加工可操作性和精度越好。目前已有的研究成果[11, 14, 18-19]推荐平台中心角一般为20°~30°。综合以上分析,本文推荐平台中心角为20°。
2.4 关于平台圆盘巴西劈裂的抗拉强度计算
确定平台中心角为20°后,就可以对岩石抗拉强度进行测定。对于α=20°的平台圆盘巴西劈裂其名义抗拉强度σt可以表示为:
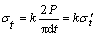 (4)
(4)
式中: k为选定的平台中心角为20°的抗拉强度计算式的修正系数。P为试件劈裂破坏时的最大荷载(N); d为岩石圆盘的直径(m);t为圆盘试件的厚度(m)。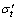 为直接拉伸时的岩石抗拉强度。所以
为直接拉伸时的岩石抗拉强度。所以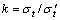 。
。
数值模拟实验操作方便、可重复性强, 因此本文基于PFC2D进行了虚拟试验仿真模拟了平台巴西劈裂和直接拉伸试验。采用如上标定过程中的参数,经过平台巴西劈裂数值实验,得到了平台中心角为20°时的名义抗拉强度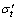 =29.5 MPa;采用同样的参数,建立模型(如图7所示,试件长60 mm,直径50 mm),对两侧球体赋恒定速度为0.01 m/s(约4×10-10 m/步)进行加载。最终试件破坏,测得直接拉伸的抗拉强度为σt=27.48 MPa。
=29.5 MPa;采用同样的参数,建立模型(如图7所示,试件长60 mm,直径50 mm),对两侧球体赋恒定速度为0.01 m/s(约4×10-10 m/步)进行加载。最终试件破坏,测得直接拉伸的抗拉强度为σt=27.48 MPa。

图6 不同平台中心角所对应的断裂形态
Fig. 6 Failure shapes of rock specimens with different central angles
最后,算得修正系数,k=0.931 5。文献[19]所给结果为0.964 4,2种方法得到的修正系数差别并不大。那么,平台中心角20°的平台巴西劈裂抗拉强度计算公式为:
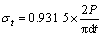 (5)
(5)

图7 数值模拟直接拉伸试验结果
Fig. 7 Result of direct tension test using particle flow code
3 结论
(1)对平台圆盘劈裂过程进行观察,发现了岩石内裂纹的形成、发展的一般过程。由于岩石的非均质性,岩石破坏单元的产生和发展是一个从无序到有序的自组织过程。
(2) 平台中心角越大,裂纹的数量越多和发展速度更快,对应的破坏模式变得复杂。对不同平台中心角的巴西劈裂分析并结合已有的研究成果,推荐平台中心角为20°。
(3) 通过比较平台巴西劈裂所得到的抗拉强度和直接拉伸所得到的抗拉强度值,计算得到平台中心角20°的平台巴西劈裂抗拉强度修正系数k=0.931 5。
参考文献:
[1] 叶明亮, 续建科, 牟宏, 等. 岩石抗拉强度试验方法的探讨[J]. 贵州工业大学学报: 自然科学版, 2001, 30(6): 19-25.
YE Mingliang, XU Jianke, MOU Hong, et al. Approach to test method of rock strength in uniaxial tension[J]. Journal of Guizhou University of Technology: Natural Science, 2001, 30(6): 19-25.
[2] ISRM. Suggested methods for determining tensile strength of rock materials[J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1978, 15(3): 99-103.
[3] GB/T 50266—99. 工程岩体试验方法标准[S].
GB/T 50266—99. Standard for tests method of engineering rock masses[S].
[4] SL264—2001. 水利水电工程岩石试验规程[S].
SL264—2001. Specifications for rock tests in water conservancy and hydro electric Engineering[S].
[5] 沈明荣. 岩体力学[M]. 上海: 同济大学出版社, 1999: 17.
SHEN Mingrong. Rock mechanics[M]. Shanghai: Tongji University Press, 1999: 17.
[6] 张少华, 缪协兴, 赵海云. 试验方法对岩石抗拉强度测定的影响[J]. 中国矿业大学学报, 1999, 28(3): 243-245.
ZHANG Shaohua, MIU Xiexing, ZHAO Haiyun. Influence of test methods on measured results of rock tensile strength[J]. Journal of China University of Mining Technology, 1999, 28(3): 243-245.
[7] 窦庆峰, 岳顺, 代高飞. 岩石直接拉伸试验与劈裂试验的对比研究[J]. 地下空间, 2004, 24(2): 178-181.
DOU Qingfeng, YUE Shun, DAI Gaofei. Experimental study on direct and indirect tension of rock[J]. Underground Space, 2004, 24(2): 178-181.
[8] 刘建锋, 徐进, 杨春和. 盐岩拉伸破坏力学特性的试验研究[J]. 岩土工程学报, 2011, 33(4): 580-586.
LIU Jianfeng, XU Jin, YANG Chunhe, et al. Mechanical characteristics of tensile failure of salt rock[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(4) : 580-586.
[9] 喻勇. 质疑岩石巴西圆盘拉伸强度试验[J]. 岩石力学与工程学报, 2005, 24(7): 1150-1157.
YU Yong. Questioning the validity of the Brazilian test for determining tensile strength of rocks[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(7): 1150-1157.
[10] Hudson J A, Brown E T, Rummel F. The controlled failure of rock discs and rings loaded in diametral compression[J]. International Journal of Rock Mechanics and Mining Sciences, 1972, 9(2): 241-244.
[11] 尤明庆, 苏承东. 平台巴西圆盘劈裂和岩石抗拉强度的试验研究[J]. 岩石力学与工程学报, 2004, 23(18): 3106-3112.
YOU Mingqing, SU Chengdong. Experimental study on split test with flattened disk and tensile strength of rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(18): 3106-3112.
[12] 喻勇, 徐跃良. 采用平台巴西圆盘试样测试岩石抗拉强度的方法[J]. 岩石力学与工程学报, 2006, 25(7): 1457-1461.
YU Yong, XU Yueliang. Method to determine tensile strength of rock using flattened Brazilian disk[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(7): 1457-1461.
[13] 尤明庆, 苏承东. 平台圆盘劈裂的理论和试验[J]. 岩石力学与工程学报, 2004, 23(1): 170-174.
YOU Mingqing, SU Chengdong. Split test of flattened rock disk and related theory[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(1): 170-174.
[14] 于庆磊, 唐春安, 杨天鸿, 等. 平台中心角对岩石抗拉强度测定影响的数值分析[J]. 岩土工程学报, 2008, 29(12): 3251-3255.
YU Qinglei, TANG Chunan, YANG Tianhong, et al. Numerical analysis of influence of central angle of flats on tensile strength of granite in split test with flattened disk[J]. Chinese Journal of Geotechnical Engineering, 2008, 29(12): 3251-3255.
[15] Cundall P A, Strack O D L. A discrete numerical model for granular assemblies[J]. International Journal of Rock Mechanics and Mining Sciences, 1979, 29(1): 47-65.
[16] Potyondy D O, Cundall P A. A bonded-particle model for rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(8): 1329-1364.
[17] 蔡美峰. 岩石力学与工程[M]. 北京: 科学出版社, 2002: 16-17.
CAI Meifeng. Rock mechanics and engineering[M]. Beijing: Science Press, 2002: 16-17.
[18] 梁正召, 唐春安, 唐世斌, 等. 岩石损伤破坏过程中分形与逾渗演化特征[J]. 岩土工程学报, 2007, 29(9): 1386-1391.
LIANG Zhengzhao, TANG Chunan, TANG Shibin, et al. Characteristics of fractal and percolation of rocks subjected to uniaxial compression during their failure process[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(9): 1386-1391.
[19] 王启智, 贾学明. 平台巴西圆盘试样确定脆性岩石的弹性模量、拉伸强度和断裂韧度—第一部分: 解析和数值结果[J]. 岩石力学与工程学报, 2002, 21(9): 1285-1289.
WANG Qizhi, JIA Xueming. Determination of elastic modulus,tensile strength and fracture toughness of brittle rocks by using flattened Brazilian disk specimen—Part I: Analytical and numerical results[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(9): 1285-1289.
(编辑 杨幼平)
收稿日期:2012-06-07;修回日期:2012-08-28
基金项目:国家自然科学基金资助项目(51174228);高等学校博士学科点专项科研基金资助项目(20090162110037)
通信作者:曹平(1959-),男,湖南祁东人,教授,博士生导师,从事岩土工程理论、试验和数值计算的研究;电话:0731-88876947;E-mail:pcao_csu@tom.com