双层空区开挖顶板稳定性的FLAC3D数值分析
何忠明1，彭振斌2，曹 平3，林 杭3
(1. 长沙理工大学 交通运输工程学院，湖南 长沙，410004；
2. 中南大学 地学与环境工程学院，湖南 长沙，410083；
3. 中南大学 资源与安全工程学院，湖南 长沙，410083)
摘 要：利用FLAC3D软件建立双层空区数值计算模型，根据厚度折减理论分析开挖后空区的安全顶板厚度和应力、变形、塑性区的分布情况，得到：安全顶板厚度与空区跨度之间符合线性关系；当跨度较小时，上部空区处于压应力状态，下部空区处于拉应力状态，最大拉应力随跨度的增大而增大；当系统达到临界状态时，上、下空区顶板的竖直位移最大，上空区的大位移区域面积明显大于下空区的大位移区域面积；空区对整体位移存在一定影响，如水平方向对整体位移的影响范围大致为跨度的1.5倍，且两空区之间存在相互作用，在大位移区域两空区显示出相互接近的趋势；当跨度较小时，上部空区顶板主要发生剪切破坏，下部空区两侧帮发生拉剪破坏，随着跨度的增大，此范围破坏形式转变为冲切破坏，整体塑性区面积明显增大，下部空区顶板塑性区逐渐发展，并延伸至上空区。
关键词：双层空区；顶板厚度；应力；变形；塑性区；数值分析
中图分类号：TU457 文献标识码：A 文章编号：1672-7207(2009)04-1066-06
Numerical analysis for roof stability of double gob area after
excavation by FLAC3D
HE Zhong-ming1, PENG Zhen-bin2, CAO Ping3, LIN Hang3
(1. School of Communication and Transportation Engineering, Changsha University of Science and Technology, Changsha 410004, China;
2. School of Geoscience and Environment Engineering, Central South University, Changsha 410083, China;
3. School of Resources and Safety Engineering, Central South University, Changsha 410083, China)
Abstract: The numerical calculation model of double gob area was founded by FLAC3D software. According to the thickness reduction theory, the safety roof thickness, stress, deformation, and plastic zones of gob area after excavation, analysis was made. The results show that the relationship between roof thickness and span of gob area is in accordance with the linear equation; when span of gob area is small, the area surrounding upper gob shows the compressive stress field, while the lower shows the tensile stress field, the maximum tensile stress increases with the increase of gob span; when the system reaches the critical state, the largest vertical displacement exhibits in the roof of gob, and the magnitude for the upper gob area is larger than that of lower gob area; excavation of rock mass has great impact on the displacement contour of whole system, the impact area is about 1.5 gob span in the horizontal direction; the two gob areas have the mutation effect to each other, which makes the big displacement area of each other move together; when span is small, the failure mode of upper gob consists mainly of shear failure, and rock mass in both side of lower gob area shows the compound failure mode consists of shear and tensile failure; with the increase of span, the failure mode changes to shear failure, and area of plastic zones becomes larger and larger; the plastic zones in the lower gob develop gradually to the upper gob.
Key words: double gob area; roof thickness; stress; deformation; plastic zone; numerical analysis
安全顶板厚度是地下采场设计的1个重要指标，其受2方面因素的影响：一是内在因素，包括空区顶板的跨度及形态，岩石的性质，岩层产状、节理、裂隙状况，以及岩石的物理力学指标等；二是外在因素，包括空区内水流搬运的机械破坏作用等。在实践中，先将上述因素加以概化，然后，采用近似方法进行计算。目前，确定地下空区顶板安全厚度的方法较多[1-4]，但基本采用简化理论分析或者传统半定量分析方法，该类方法只能对简单几何边界和外力边界情况进行分析，其应用范围受到一定限制。近年来，随着计算机技术的不断发展，许多学者开始采用数值方法研究岩土工程问题[5-7]。采用数值方法可模拟复杂的边界条件，且能分析地下空区顶板应力与变形的具体情况，将其用于地下空区开挖稳定性的分析是1种较好的研究方法[8-13]。如林杭等[3]根据边坡强度折减法的思想提出了空区安全顶板预测的厚度折减法；高峰等[8]在分析影响矿体顶板稳定性因素的基础上，通过建立有限元数值模型和多次模拟计算得出了不同影响因素组合下顶板的安全厚度；王勇等[10]采用二维弹塑性有限元方法对隧道开挖进行数值模拟计算，分析了隧道底部溶洞顶板安全厚度的影响因素；胡卸文等[11]通过逐渐调整上部荷载，使其达到临界状态下的数值模拟方法，分析不同影响因素对人防地道顶板最大安全荷载的影响及相关变化规律。在此，本文作者基于厚度折减理论采用三维快速拉格朗日差分法(FLAC3D软件)对某双层空区开挖稳定性进行分析。
1 计算方法
1.1 安全顶板厚度的确定方法
根据空区顶板结构的完整性，可将顶板分为完整顶板和不完整顶板。完整顶板是指未被节理裂隙切割或虽被切割但是胶结良好的情况，否则，为不完整顶板。完整顶板一般破坏发生在顶板本身，其破坏方式有2种：拉伸破坏和剪切破坏。由于岩体是一种“不抗拉材料”(即抗拉强度很低)，一般首先发生拉伸破坏，然后，裂缝扩展并与地表贯通而后发生剪切破坏(冲剪破坏)。由于地下空区顶板的形状千变万化，实际空区形状可从很不规则到规则，在进行力学分析时，为了简化计算，可将地下空区简化成长方体洞室或矩形截面洞室(长轴很长或为平面问题)、球形洞室或圆形隧道，对于矩形界面洞室或圆形隧道可按平面问题考虑，对球形洞室则应按空间问题考虑，而对长方体洞室，可根据其顶板分布范围来计算。本文视顶板具有完整性，并将地下空区简化为长方形，按平面应变问题进行考虑。根据林杭等[3]提出的厚度折减法，采用优化理论中的二分法对顶板厚度进行预测，以安全系数为1.3作为计算安全顶板厚度的标准，以计算不收敛作为系统失稳判据，即不平衡力比率(节点平均内力与最大不平衡力的比值)无法满足10-5的求解要求，具体计算流程如图1所示。
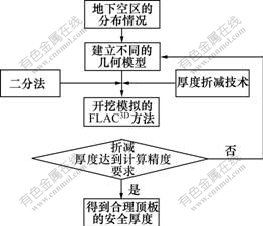
图1 顶板安全厚度确定流程图
Fig.1 Algorithmic flow chart for solution of roof safety thickness
1.2 岩土介质的理想弹塑性模型
Mohr-Coulomb准则是目前岩土工程中应用最为广泛的破坏准则，其表达式为[14]：
2 数值模型
2.1 基本假设
利用基于厚度折减理论的FLAC3D程序对开挖过程中地下空区顶板稳定性进行分析，其基本假设如下：
a. 地下空区的围岩是均质各向同性的地下空间半无限体。
b. 地下空区充填物强度与岩体相比很低，对受力分析影响很小。所以，分析中按空洞进行计算，充填物仅作为安全储备。
c. 模拟地下空区的开挖采用一次性开挖完毕的方法。
d. 假定采空区形状为矩形，并将群采空区等效为1个单跨度的采空区。
2.2 工程概况
根据某磷矿穿岩矿段地下采空区量测结果，在计算采空区安全顶板厚度时，A和B 2层矿都含有开采的空区，考虑其相互作用关系，在计算中也只考虑2层空区的情况。岩组自上而下分别为：
a. 顶板白云岩。浅灰色薄层状含磷白云岩，部分地段因磷块岩条带较多而形成白云质磷块岩，厚度比较稳定，大体呈南厚北薄，为矿层的直接顶板。
b. B层磷块岩。由深灰、灰黑色碎屑状白云质磷块岩(包括条带、条纹、团块、碎屑状)和黑色致密块状及泥质磷块岩组成，厚度稳定。
c. 夹层白云岩。浅灰色中层状含磷微粒白云岩，顶部具不稳定的硅质团块或含磷硅质团块，赋存有不稳定的白云质磷块岩透镜体，厚度变化规律是：北薄南厚，东薄西厚。
d. A层磷块岩。为灰黑色薄板状砂泥质磷块岩，顶底具不稳定的条带状白云质磷块岩，厚度由南东向北西渐次变薄，直至尖灭。
e. 底板白云岩。浅灰色中厚层状细粒白云岩。
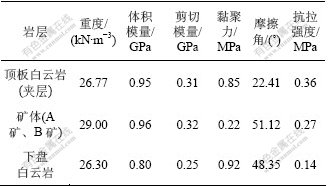
目前，采空区位于B层矿，具体计算模型见图2，另考虑边界效应，分别往空区左右两边延伸的距离为跨度的8倍。计算参数如表1所示。整体应力场按照自重应力场考虑，为了模拟真实开挖情况，首先，施加初始应力场，计算系统以达到平衡状态；然后，将节点位移和速率清为0；最后，计算采空区后的应力变形情况；计算荷载考虑1台225 t挖掘机作业时对台阶面的压力，挖掘机的履带长为6 m，宽为1 m，将挖掘机的重力转换成等效荷载，为q=187.5 kPa，而考虑动载的影响时，计算荷载取为q的1.3倍，即243.75 kPa。
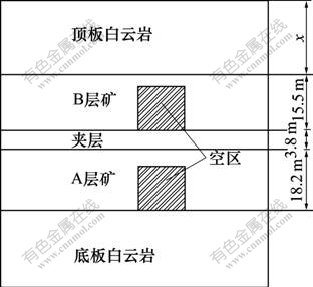
图2 二层空区计算模型
Fig.2 Calculation model for double gob area
表1 计算参数
Table 1 Calculation parameters
3 结果与讨论
3.1 顶板安全厚度的计算
通过试算得到，同一跨度空区采高对安全顶板厚度有一定的影响，但影响不大，考虑到在A和B 2层矿中留下的采空区实际情况，以A和B矿层内采空区的采高都以8 m为例，计算A和B矿层内采空区跨度都为4，7，10和15 m时的安全顶板厚度，所得安全顶厚度分别为2.5，6.5，10.0和14.1 m。
图3所示为安全顶板厚度与跨度的关系。可以看出，随着空区跨度的增大，安全顶板厚度也逐渐增大，二者基本呈线性关系。因此，采用下式对其进行拟合：
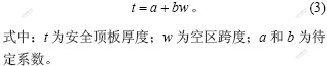拟合结果表明：当a=-1.147 73，b=1.046 97时，拟合的相关系数为0.992 74，属于高度相关；当空区最小跨度为4 m时，其对应的安全顶板厚度为 2.5 m，但考虑到顶板岩体本身可能存在节理裂隙等，顶板最小安全厚度也不宜过小，在实际工程中，将跨度为4 m的顶板最小安全厚度定为3 m。
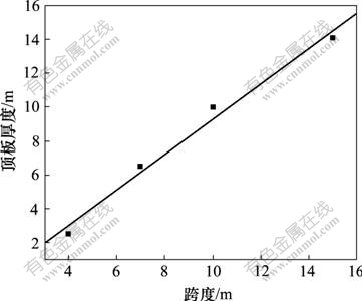
图3 安全顶板厚度与跨度的关系
Fig.3 Relationship between span and roof thickness of gob
3.2 应力分析
图4所示为不同跨度时的最大主应力分布。可以看出，由于几何模型和边界条件对称布置，得到的应力分布也呈现对称形态。当跨度较小时，上部空区主要处于压应力状态，下部空区处于拉应力状态，跨度为4，7和15 m时对应的最大拉应力分别为0.075，0.134和0.397 MPa，说明最大拉应力随跨度的增大而增大；并且从跨度为15 m的空区中可以看出，拉应力的分布区域也发生变化，从下部空区逐渐延伸到上部空区周围。
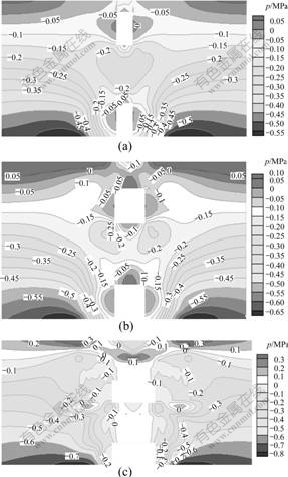
最小跨度/m: (a) 4; (b) 7; (c) 15
图4 最大主应力分布
Fig.4 Maximum stress distribution
3.3 位移趋势
图5所示为开挖过程中的竖直位移分布。可以看出，当系统达到临界状态时，上下空区顶板的位移最大，并且上空区大位移区域的面积明显大于下空区大位移区域面积，空区对整体的位移存在一定的影响范围，跨度为4 m和15 m对应的影响范围分别为水平方向13 m和45 m左右，以空区中心向外延伸1.5倍左右，在实际开采过程中，可对此范围内的位移进行监测，以指导施工。
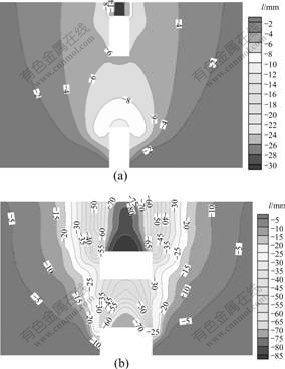
跨度/m: (a) 4; (b) 15
图5 竖直位移分布
Fig.5 Vertical displacement distribution
图6所示为跨度15 m时的水平位移分布。可以看出，空区的开挖引起岩体较为明显的水平位移，其趋势为向空区内部移动；上部空区最大的水平位移位于两帮中下部，下部空区的最大位移位于两帮的中上部，并且下空区两顶点略上处存在2处明显的大位移区域，这是由于2个空区之间存在相互作用，以至大位移区域显示出相互接近的趋势；另外，地面受到空区开挖的影响也出现往整体中央挤压的水平位移。
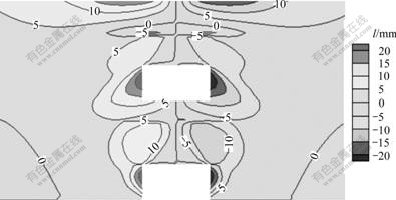
图6 15 m跨度水平位移分布
Fig.6 Horizontal displacement distribution for 15 m span
3.4 塑性区分析
图7所示为塑性区分布。可见，当跨度较小时，上部空区顶板主要发生剪切破坏，下部空区两侧帮主要发生拉剪破坏，破坏范围似蝴蝶状；随着跨度的增大，此范围的破坏形式转变为冲切破坏，这是由于跨度较小时空区的高度大于其跨度，在水平应力的作用下，两帮向空区内鼓胀，发生拉剪破坏；随着跨度的增大，跨度逐渐大于高度，在竖直应力的作用下，两侧帮的鼓胀受到上部应力的约束，受到限制，破坏形式转变为剪切破坏，整体塑性区面积明显增大，下部空区顶板塑性区逐渐发展，并出现延伸至上空区的趋势。另外，对比跨度为4~15 m时的塑性区面积可以看出，在4~10 m范围内塑性区面积发展较平缓；当跨度达到15 m时，塑性区面积发生明显突变。
跨度/m: (a) 4; (b) 7; (c) 10; (d) 15
图7 塑性区分布
Fig.7 Plastic zone distribution
4 结 论
a. 根据某矿穿岩矿段采空区分区的特点，建立双采空区模型，基于厚度折减法，利用FLAC3D软件，以计算不收敛为破坏准则，计算地下采空区跨度为4，7，10和15 m时对应的安全顶板厚度分别为2.5，6.5，10和14.1 m，两者之间符合线性关系。
b. 当跨度较小时，上部空区主要处于压应力状态，下部空区处于拉应力状态；最大拉应力随跨度的增大而增大；当系统达到临界状态时，上、下空区顶板的竖直位移最大，并且上空区大位移区域的面积明显大于下空区大位移区域的面积，空区对整体的位移存在一定的影响范围，大致为空区跨度的1.5倍；两空区之间存在相互作用，在大位移区域，两空区之间显示出相互接近的趋势；当跨度较小时，上部空区顶板主要发生剪切破坏，下部空区两侧帮主要发生拉剪破坏，破坏范围似蝴蝶状；随着跨度的增大，此范围的破坏形式转变为冲切破坏，整体塑性区面积明显增大，下部空区顶板塑性区逐渐发展，并出现延伸至上空区的趋势。
参考文献：
[1] 周建普, 李献民. 岩溶地基稳定性分析评价方法[J]. 矿冶工程, 2003, 23(1): 4-8.
ZHOU Jian-pu, LI Xian-min. Methods of stability analysis in karst foundation[J]. Mining and Metallurgical Engineering, 2003, 23(1): 4-8.
[2] 黎 斌, 范秋雁, 秦风荣. 岩溶地区溶洞顶板稳定性分析[J]. 岩石力学与工程学报, 2002, 21(4): 532-536.
LI Bin, FAN Qiu-yan, QIN Feng-rong. Analysis on roof stability of karst cave in karst areas[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(4): 532-536.
[3] 林 杭, 曹 平, 李江腾, 等. 采空区临界安全顶板预测的厚度折减法[J]. 煤炭学报, 2009, 34(1): 53-57.
LIN Hang, CAO Ping, LI Jiang-teng, et al. The thickness reduction method in forecasting the critical safety roof thickness of gob area[J]. Journal of China Coal Society, 2009, 34(1): 53-57.
[4] 李智毅. 工程地质学基础[M]. 武汉: 中国地质大学出版社, 1990.
LI Zhi-yi. Engineering geology base[M]. Wuhan: China Geology University Press, 1990.
[5] 郭 群. 层状岩石强度特征及其数值实现[J]. 科技导报, 2008, 26(16): 68-71.
GUO Qun. Strength characteristic of stratified rock and its numerical application[J]. Science and Technology Review, 2008, 26(16): 68-71.
[6] XU Guo-yuan, YAN Chang-bin. Numerical simulation for influence of excavation and blasting vibration on stability of mined-out area[J]. Journal of Central South University of Technology, 2006, 13(5): 577-583.
[7] 程 晔, 赵明华, 曹文贵. 基桩下溶洞顶板稳定性评价的强度折减有限元法[J]. 岩土工程学报, 2005, 27(1): 38-41.
CHENG Ye, ZHAO Ming-hua, CAO Wen-gui. Study on stability evaluation of karst cave roof with strength reduction FEM[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(1): 38-41.
[8] 高 峰, 周科平, 胡建华, 等. 充填体下矿体开采安全顶板厚度数学预测模型[J]. 岩土力学, 2008, 29(1): 177-181.
GAO Feng, ZHOU Ke-ping, HU Jian-hua, et al. Mathematical forecasting model of safety thickness of roof for mining orebody under the complicated backfilling[J]. Rock and Soil Mechanics, 2008, 29(1): 177-181.
[9] 周科平, 苏家红, 古德生, 等. 复杂充填体下矿体开采安全顶板厚度非线性预测方法[J]. 中南大学学报: 自然科学版, 2005, 36(6): 1094-1099.
ZHOU Ke-ping, SU Jia-hong, GU De-sheng, et al. The nonlinear forecasting method of the least security coping thickness when mining under complex filling body[J]. Journal of Central South University: Science and Technology, 2005, 36(6): 1094-1099.
[10] 王 勇, 乔春生, 孙彩红, 等. 基于SVM的溶洞顶板安全厚度智能预测模型[J]. 岩土力学, 2006, 27(6): 1000-1004.
WANG Yong, QIAO Chun-sheng, SUN Cai-hong, et al. Forecasting model of safe thickness for roof of karst cave tunnel based on support vector machines[J]. Rock and Soil Mechanics, 2006, 27(6): 1000-1004.
[11] 胡卸文, 陈 光. 综合考虑各影响因素下浅埋洞室顶板最大安全荷载预测[J]. 中国铁道科学, 2005, 26(4): 68-72.
HU Xie-wen, CHEN Guang. Forecasting maximum safety loading of roof in shallow underground excavation under different conditions[J]. China Railway Science, 2005, 26(4): 68-72.
[12] 李廷春, 李术才, 邱祥波, 等. 三维快速拉格朗日法在安全顶板厚度研究中的应用[J]. 岩土力学, 2004, 25(6): 935-939.
LI Ting-chun, LI Shu-cai, QIU Xiang-bo, et al. Application of fast lagrangian analysis of continua to researching on safe rock covers of Xiamen subsea tunnel[J]. Rock and Soil Mechanics,, 2004, 25(6): 935-939.
[13] 曹文贵, 程 晔, 赵明华. 公路路基岩溶顶板安全厚度确定的数值流形方法研究[J]. 岩土工程学报, 2005, 27(6): 621-625.
CAO Wen-gui, CHENG Ye, ZHAO Ming-hua. Studies on numerical manifold method for determination of safe thickness of karst roof in roadbed[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(6): 621-625.
[14] Itasca Consulting Group. Theory and Background[R]. Minnesota: Itasca Consulting Group, 2002.
收稿日期：2008-07-10；修回日期：2008-10-08
基金项目：国家自然科学基金资助项目(50774093)；长沙理工大学人才引进基金资助项目(2009年)
通信作者：何忠明(1980-)，男，湖南永兴人，博士，从事道路工程、岩土工程研究；电话：13055178045；E-mail: hezhongming45@126.com
