J. Cent. South Univ. (2017) 24: 2294-2305

DOI: https://doi.org/10.1007/s11771-017-3641-3

Performance analysis of high-static-low-dynamic stiffness vibration isolator with time-delayed displacement feedback

CHENG Chun(程春), LI Shun-ming(李舜酩), WANG Yong(王勇), JIANG Xing-xing(江星星)

College of Energy and Power Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China

Central South University Press and Springer-Verlag GmbH Germany 2017

Abstract: The displacement feedback with time delay considered is introduced in order to enhance the vibration isolation performance of a high-static-low-dynamic stiffness (HSLDS) vibration isolator. Such feedback is detailedly analyzed from the viewpoint of equivalent damping. Firstly, the primary resonance of the controlled HSLDS vibration isolator subjected to a harmonic force excitation is obtained based on the multiple scales method and further verified by numerical integration. The stability of the primary resonance is subsequently investigated. Then, the equivalent damping is defined to study the effects of feedback gain and time delay on primary resonance. The condition of jump avoidance is obtained with the purpose of eliminating the adverse effects induced by jumps. Finally, the force transmissibility of the controlled HSLDS vibration isolator is defined to evaluate its isolation performance. It is shown that an appropriate choice of feedback parameters can effectively suppress the force transmissibility in resonant region and reduce the resonance frequency. Furthermore, a wider vibration isolation frequency bandwidth can be achieved compared to the passive HSLDS vibration isolator.

Key words: vibration isolator; high-static-low-dynamic stiffness; piecewise nonlinear; time-delayed feedback; multiple scales method

1 Introduction

Passive nonlinear vibration isolators with high- static-low-dynamic stiffness (HSLDS) property have drawn increasing attentions and have been studied for many years, since they outperform the linear counterparts for the ability of providing lower isolation frequency and maintaining a small static deflection without sacrificing the load bearing capacity. The HSLDS vibration isolators are usually comprised of a vertical spring and the negative stiffness mechanisms which are also called the stiffness correctors. With structural parameters of vibration isolators properly designed, the HSLDS property can be achieved at the static equilibrium position. IBRAHIM [1] summarized a comprehensive review of passive nonlinear vibration isolators, shedding light on a variety of stiffness correctors. PLATUS [2] built a HSLDS vibration isolator using axially compressed beams as stiffness corrector for low-frequency vibration isolation. CARRELLA et al [3, 4] made the static analysis and studied the isolation performance of a HSLDS vibration isolator comprised of a vertical spring and two oblique springs. ROBERTSON et al [5], ZHOU and LIU [6] and XU et al [7] proposed HSLDS vibration isolators using electromagnetic or magnetic devices as stiffness correctors and investigated the dynamic behavior theoretically and experimentally. LIU et al [8] and HUANG et al [9] built the HSLDS vibration isolator using Euler buckled beams as stiffness corrector and investigated the dynamic behavior and isolation performance detailedly. SHAW et al [10] built a HSLDS vibration isolator using a bistable composite plate as stiffness corrector and studied the isolation performance experimentally. Recently, ZHOU et al [11] and CHENG et al [12] studied the dynamic behavior of a HSLDS vibration isolator using the cam-roller-spring mechanism as stiffness corrector. The aforementioned researches demonstrate that the HSLDS vibration isolators can achieve better isolation performance than the equivalent linear counterparts when the excitation amplitude is relatively small.

Due to the existence of cubic stiffness nonlinearity in the HSLDS vibration isolators, the resonance frequency and peak amplitude increase accordingly with the increase of excitation amplitude. The large vibration amplitude and poor isolation performance are adverse to the protected equipments. As is known, increasing the linear damping can effectively reduce the response amplitude in resonant region, as a result, the transmissibility increases in the frequency region where the isolation is required. With the purpose of overcoming the above contradiction, a great deal of active control techniques are used to control the vibration [13–20]. HU et al [13] studied the primary resonance and 1/3 subharmonic resonance of a harmonically forced Duffing oscillator with time-delayed state feedback control and discussed vibration control from the viewpoint of equivalent damping. ELLIOTT et al [14] investigated the stability and isolation performance of an active vibration system with velocity feedback. Such feedback control can create the sky-hook damping, in which the amplitude in resonant region can be effectively reduced with the isolation performance in higher frequencies unaffected. However, as demonstrated in Ref. [15], such control strategy may lead to a sharp increase in damping force, which inevitably results in a jerk in the acceleration response. LI et al [16] designed the cubic velocity feedback controller in a nonlinear oscillator to control the jump phenomenon and the unstable region. GAO and CHEN [17], HUANG et al [18] introduced the time-delayed cubic velocity feedback in the non-smooth systems. It is demonstrated that such feedback control can suppress the resonance response without the jerk and the isolation performance in higher frequencies remains unaffected. WANG et al [19] also introduced the time-delayed cubic velocity feedback in the HSLDS vibration isolator and achieved better isolation performance. SUN et al [20] introduced the time-delayed displacement feedback in a HSLDS vibration isolator and carried out the stability and bifurcation analysis. They also simply investigated the effect of time delay on the isolation performance, however, the effect of feedback gain on the dynamic response needs to be further studied. With the purpose of controlling vibration and enhancing the isolation performance, the time- delayed displacement feedback control is introduced in this work for a HSLDS vibration isolator which has been previously studied in the Refs. [11] and [12]. Compared to other active control strategies, the time-delayed displacement feedback control can not only suppress the resonance response but also broaden the vibration isolation bandwidth.

2 Mathematic model and static analysis

The schematic diagram of the HSLDS vibration isolator with time-delayed displacement feedback is shown in Fig. 1. The lumped mass M is supported above the base by a vertical spring with stiffness K_v and is initially at the static equilibrium position; the cam- roller-spring mechanism which is used to provide the negative stiffness is composed of a semicircular cam with radius r₂, a roller with radius r₁ and a horizontal pre-compressed spring with stiffness K_h; X(t) is the displacement of the mass from the static equilibrium position and can be measured by a sensor; C denotes the linear damping coefficient of the damper; the displacement signal X(t) can be converted into displacement control force through the controller and actuator, where the actuator can be achieved by the combination of a control spring and a servo motor, which provides an active feedback force. The time delay is considered due to the time spent in measuring system state, calculating and executing the control force.

Fig. 1 Schematic diagram of HSLDS vibration isolator with time-delayed displacement feedback (1–Sensor; 2–Controller; 3–Cam-roller-spring mechanism; 4–Actuator)

When the vibration isolator works, the rollers roll on the cams back and forth with horizontal springs sliding in the horizontal direction. Therefore, the negative stiffness can be achieved in the vertical direction. The stiffness of the vibration isolator can be piecewise nonlinear or continuous depending on the excitation amplitude.

The relationship between the restoring force and displacement for the HSLDS vibration isolator with piecewise nonlinear characteristic is given by [11]

     (1)

where L denotes the pre-compression length of the horizontal springs, X_d indicates the critical value corresponding to the discontinuity points.

Equation (1) can be transformed into the non-dimensional form.

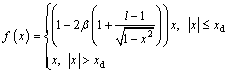      (2)

where

Considering small oscillations about the static equilibrium position, the non-dimensional stiffness of the HSLDS system can be obtained by differentiating the first expression of Eq. (2) with respect to x.

                     (3)

The non-dimensional stiffness at the static equilibrium position can be obtained by substituting x=0 into Eq. (3)

                                 (4)

If the stiffness of the HSLDS system is zero at the static equilibrium position, then the quasi-zero stiffness (QZS) property can be obtained, hence the QZS condition is given by setting k_s=0

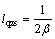                                   (5)

The non-dimensional restoring force and stiffness as a function of displacement for various l when 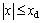are shown in Fig. 2, where the red solid lines denote the QZS property. It can be seen that the stiffness at the static equilibrium position is getting smaller with the increase of l. When l increases to l_qzs, the minimum stiffness becomes zero, therefore, the QZS property is achieved. If l increases further, the stiffness in the vicinity of the static equilibrium position becomes negative, thus the system can be unstable which is undesirable in practice. In order to avoid the unstable system, l should be equal to or smaller than l_qzs. The case lqzs is considered in this work. Therefore, the vibrating system has the common HSLDS characteristics.

Considering small oscillations about the static equilibrium position, the first expression of Eq. (2) can be approximated by a third-order Taylor series expansion at x=0 for simplicity

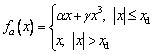                  (6)

where

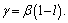
The non-dimensional exact force-displacement curve of Eq. (2) and its approximation of Eq. (6) are shown in Fig. 3. It can be seen that the restoring force undergoes a finite jump at the discontinuity points 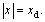Obviously, the approximate restoring force matches well with the exact one.

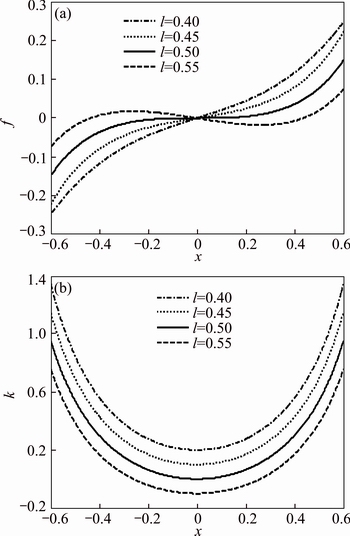
Fig. 2 Non-dimensional force-displacement (a) and stiffness- displacement (b) curves for various l when x_d=0.6, β=1

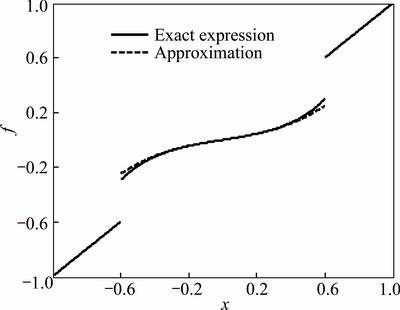
Fig. 3 Comparison of exact and approximate force- displacement curves when x_d=0.6, l=0.4, β=1

3 Multi-scale analysis

3.1 Primary resonance

The controlled HSLDS system is subjected to a force excitation 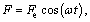where F_e and ω denote the excitation amplitude and frequency, respectively. Therefore, the equation of motion of the mass considering the time-delayed displacement feedback is given as follows:

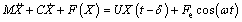       (7)

where F(X) is the exact restoring force given by Eq. (1), U and δ denote the feedback gain and time delay, respectively, and the primes denote derivatives with respect to t. Replacing the exact restoring force by the approximation and writing Eq. (7) in the non-dimensional form yield

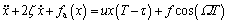         (8)

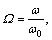
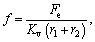
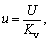
where and where the primes denote derivatives with respect to T, and f_a(x) is the approximate restoring force defined by Eq. (6).

With the purpose of obtaining the primary resonance of the controlled HSLDS system by using the multiple scales method, it is assumed that

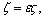
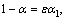
                                 (9)

where ε is a small parameter, σ is a detuning frequency. Substituting Eq. (9) into Eq. (8) yields

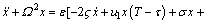
                     (10)

where

                 (11)

The approximate solution of Eq. (10) is assumed to be in the form of

               (12)

where T₀=T is a fast time scale and T₁=εT is a slow time scale. Introducing the following differential operators

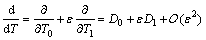
                  (13)

Substituting Eq. (12) and Eq. (13) into Eq. (10) and equating the same power of ε yield

           (14a)

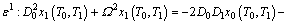
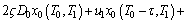
   (14b)

The solution of Eq. (14a) can be expressed as

            (15)

where 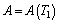is the response amplitude and θ=θ(T₁) is the phase, and they are functions of slow time scale T₁.

Substituting Eq. (15) into Eq. (14b) yields

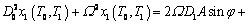
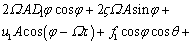
 (16)

where G₁ and G₂ are the Fourier coefficients of the basic harmonic terms of

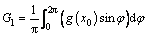                   (17a)

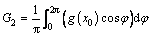                  (17b)

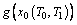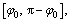
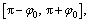
Due to the fact that is a piecewise nonlinear function, thus the integral should be calculated respectively in the intervals: 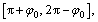where corresponds to the phase of discontinuity point in a vibration period. Thus the coefficients can be derived.

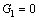                                    (18a)

(18b)

In order to eliminate the secular term in Eq. (16), the coefficients of sinφ and cosφ should be zero. Therefore, a set of autonomous differential equations that govern the amplitude and phase can be obtained

     (19a)

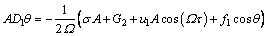 (19b)

The steady-state solutions can be obtained by setting Then, the following equation can be derived

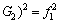                (20)

Multiplying both sides of Eq. (20) by ε² yields the amplitude-frequency equation

                           (21)

To verify the validity of the multiple scales method, the fourth-order Runge-Kutta scheme is used. And the fast Fourier transform (FFT) technique is utilized to obtain the basic harmonic term of the response. The parameters of HSLDS system are set as x_d=0.6, β=1, l=0.4, ζ=0.02, unless otherwise stated. The comparison between analytical solutions and numerical simulation is shown in Figs. 4 and 5. It can be seen that there is excellent agreement between analytical solutions and numerical results. Note that numerical results in some frequency bands cannot be obtained due to their instability, which will be investigated detailedly in the next subsection.

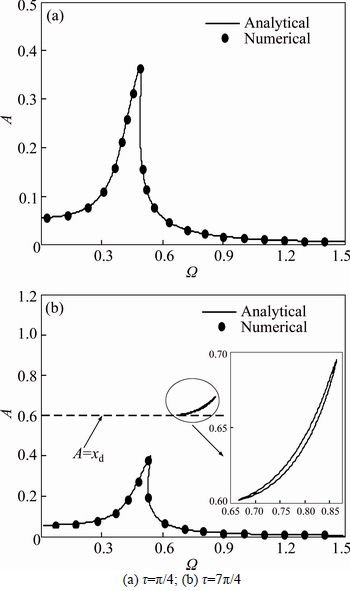
Fig. 4 Amplitude-frequency curves of primary resonance for different time delays when f=0.01, u=0.02:

3.2 Stability analysis

For the steady-state solutions, the following equations can be obtained.

               (22a)

Fig. 5 Amplitude-frequency curves of primary resonance for different time delays when f=0.05, u=0.02:

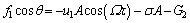             (22b)

In order to investigate the stability of the steady- state solutions, linearizing Eqs. (19a) and (19b) with respect to A and φ, respectively, and combining Eqs. (22a) and (22b) yield

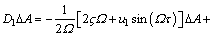
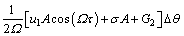         (23a)

              (23b)

where 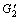is the derivative of G₂ with respect to A, and its expression is given by

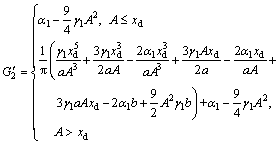  (24)

where

The characteristic equation of the coefficient matrix of Eqs. (23a) and (23b) is given by

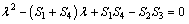              (25)

where

            (26a)

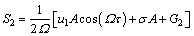            (26b)

            (26c)

According to the Routh-Hurwitz criterion [21], the steady-state solution is asymptotically stable if and only if the following two conditions hold simultaneously:

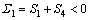                            (27a)

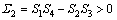                        (27b)

The amplitude-frequency curves with stability boundaries for different excitation amplitudes are shown in Fig. 6, where M and N denote the unstable regions obtained by Σ₁ is independent of response amplitude, and Σ₁<0 always holds for specified system parameters. For the frequency island surrounded by a black circle, the lower branch is covered by the region N, indicating its instability. In fact, if only condition (27a) is satisfied but inequality (27b) does not stand up, the steady-state solution will lose stability due to the occurrence of saddle-node bifurcation, which means the jump phenomenon could happen.

4 Effects of feedback parameters on primary resonance

4.1 Equivalent damping

In order to investigate the effects of feedback parameters on primary resonance from the viewpoint of equivalent damping, Eq. (21) is written as

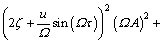
    (28)

Therefore, the equivalent damping ratio and equivalent resonance frequency can be defined as

                       (29)

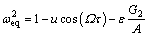                    (30)

As shown in Eq. (29), the equivalent damping ratio is independent of response amplitude. Only the positive displacement feedback gain is considered here, thus the extreme values of the equivalent damping ratio can be obtained

                            (31a)

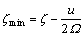                             (31b)

In resonant region, . Then, the equivalent damping ratio can be approximated as

                           (32)

Obviously, when τ lies in [0, π], the following inequality is obtained

                           (33)

Note that ζ_eq is greater than ζ, and ζ is the damping ratio of the uncontrolled system. As a result, the displacement feedback with non-zero time delay has the function of increasing the damping ratio and is more efficient than that without time delay, which can be verified in Fig. 7.

Fig. 6 Amplitude-frequency curves with stability boundaries for different excitation amplitudes when u=0.02, τ=7π/4:

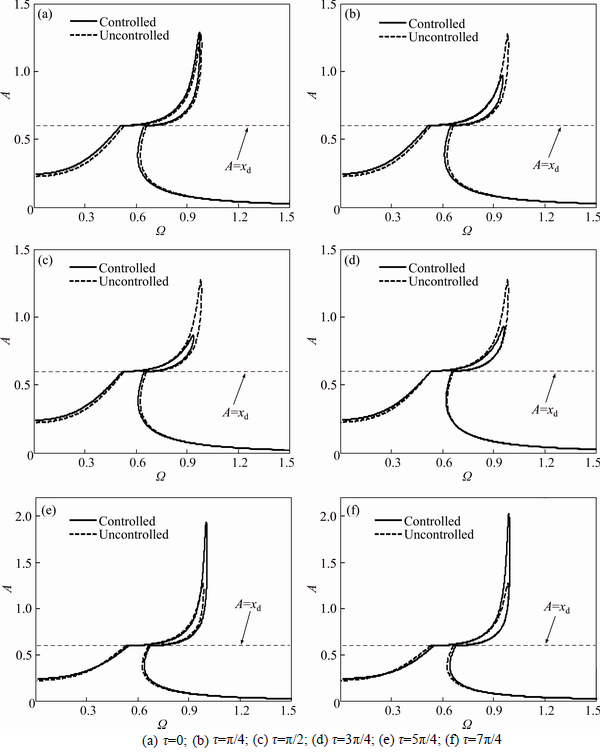
Fig. 7 Comparison of amplitude-frequency curves of controlled system and uncontrolled system when f=0.05, u=0.02:

However, when τ lies in [π, 2π], the inequality is given as

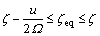                           (34)

It can be seen that the equivalent damping ratio ζ_eq is even smaller than the linear damping ratio of the uncontrolled system in this case, which means the displacement feedback fails to suppress the vibration. As a result, the response amplitude in resonant region is increased compared to the uncontrolled system.

4.2 Effects of feedback parameters on primary resonance

In this subsection, the effects of time delay and feedback gain on primary resonance are mainly analyzed. The effect of time delay on primary resonance in the range of [0, 2π] is shown in Fig. 7. When there is no time delay for the controlled system (τ=0), as shown in Fig. 7(a), the peak value of the amplitude-frequency curve hardly changes but the resonance frequency shifts slightly towards the lower frequency region. The top three figures demonstrate that the effect of vibration suppression is getting better with the increase of time delay when τ lies in [0, π/2]. Generally, when τ lies in [0, π], such feedback always takes effect due to the fact that the equivalent damping ratio ζ_eq is greater than ζ. As τ increases further and lies in [π, 2π], ζ_eq is less than ζ, then the response amplitude in resonant region fails to be suppressed compared to the uncontrolled system.

The influence of feedback gain on primary resonance is shown in Fig. 8. For the case of τ=π/4, when the feedback gain increases, the response amplitudes in resonant region are efficiently suppressed, and the response amplitudes in lower frequencies increase gradually. In addition, the resonance frequency and the frequencies which correspond to the discontinuity points shift towards lower frequency. Then, for the case of τ=3π/4, when the feedback gain increases, the response amplitudes in resonant region decrease accordingly, and the resonance frequency shifts towards lower frequency. It is worth noting that when the feedback gain increases to u=0.1, the peak amplitude is lower than the critical displacement x_d. Therefore, the rollers will keep the contact state with the cams and excellent performance can be obtained. In fact, when τ lies in [0, π], according to Eq. (32) the equivalent damping ratio ζ_eq is the increasing function of u. Therefore, the greater the feedback gain, the better the control effect.

Figure 9 shows the effect of time delay on the response amplitude at Ω=0.9 for various feedback gains.

Fig. 8 Comparison of amplitude-frequency curves of controlled system for various feedback gains when f=0.05:

Fig. 9 Effect of time delay on response amplitude and stability boundary for various feedback gains when f=0.05, Ω=0.9:

The gray regions marked with N denote the instability of steady-state response obtained by Σ₂<0 and the unstable regions marked with Q are obtained by Σ₁>0. For the case of u=0.02, there are three steady-state solutions for the specified frequency and one of solution branches is absolutely covered by the unstable region N. Thus the response on this branch is always unstable for any time delay. For the case of u=0.03, the distance between the upper two solution branches becomes closer. However, the middle solution branch is still covered by the unstable region. When the feedback gain increases to u=0.1, the upper two solution branches are replaced by a closed loop and most of the loop is covered by unstable regions N and Q. The intersections between the steady-state solutions and unstable boundary N indicate the occurrence of jump phenomenon. Interestingly, when the feedback gain increases further to u=0.13, as shown in Fig. 9(d), one closed loop is divided into two loops. As a result, when time delay varies in a period of 2π, the controlled system will experience more jumps at the specified frequency.

For a vibration isolation system, the response amplitudes in resonant region should be suppressed under a target level. Figure 10 gives a design illustration of feedback gain and time delay to suppress the response amplitude at Ω=0.9 with a target no more than A_c=0.7 when f=0.05, where the thick line denotes the division of A_c=0.7 and the unstable region is obtained by Σ₁>0. The whole plane is divided into two parts by the division line and the response amplitude governed by parameter pair (τ, u) on the upper plane is less than the target value. Therefore, the upper plane indicates the feasible parameter combinations. However, not all parameter pairs located in the upper plane can satisfy the stability condition. Thus, the feedback parameters located in the unstable region should be excluded.

The aforementioned analysis in this subsection indicates that the feedback gain and time delay have obvious influence on the primary resonance of the controlled system. An appropriate choice of feedback parameters can efficiently suppress the response amplitude in resonant region and reduce the resonance frequency.

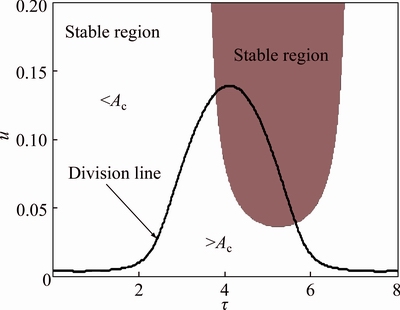
Fig. 10 Design illustration of feedback gain and time delay for f=0.05, Ω=0.9, A_c=0.7

5 Jump avoidance

The excitation frequency may fluctuate within a certain range in practice, therefore, if the system parameters cannot be properly chosen, the system would undergo the jump phenomenon. Due to the undesirable effects of jumps on the equipments that need to be protected, it is necessary to find the condition of jump avoidance [22, 23].

In order to obtain the jump avoidance condition, the jump points should be first determined through dΩ/dA=0. If there are solutions for the derivative, the jumps exist, otherwise, the jumps are avoided. Therefore, there exists a critical boundary that separates the non solution area and multiple solution area.

For simplicity, the amplitude-frequency equation can be written in the following form:

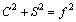                               (35)

where

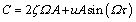                     (36a)

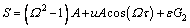             (36b)

Differentiating both sides of Eq. (21) with respect to A yields

                   (37)

Substituting dΩ/dA=0 into Eq. (37), the following equation can be obtained

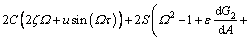
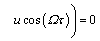                       (38)

where 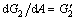and its detailed expression is given by Eq. (24). Thus the jump frequency and amplitude for the given parameters can be determined by combining Eq. (21) and Eq. (38). However, they are the complex transcendental equations due to the fact that Ω appears in the trigonometric function, which means the solutions cannot be obtained analytically.

Therefore, a numerical scheme, Levenberg- Marquardt optimization algorithm, is introduced. This optimization algorithm can be easily achieved with the help of MATLAB software. Figure 11 shows the jump amplitude as a function of excitation amplitude f when τ=π/4 and τ=3π/4, respectively. f_cr is the critical excitation force at which the jumps can be avoided. For the case of τ=π/4, if the excitation amplitude exceeds the critical value (f_cr=0.0079), there are two amplitudes corresponding to the jump-down and jump-up points, which means the jumps exist. But when f<0.0079, there is no solution and thus no jump. Similarly, for the case of τ=3π/4, we get f_cr=0.0142. Therefore, if f>f_cr, the jumps occur, otherwise, the jumps are avoided.

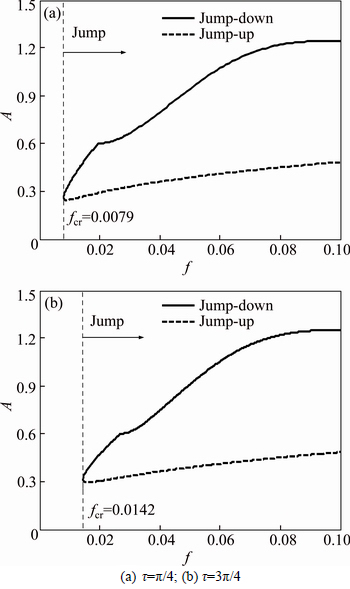
Fig. 11 Jump points and critical border f_cr when u=0.02:

Figure 12 shows the amplitude-frequency curves of the controlled system for different excitation amplitude for the case of τ=π/4 and τ=3π/4, where the black dots denote the jump-down and jump-up points when the excitation amplitude is greater than f_cr. Obviously, these two cases give us a clear illustration of the effect of excitation amplitude on jump phenomenon.

6 Force transmissibility

With the purpose of evaluating the isolation performance of the controlled HSLDS vibration isolator,the force transmissibility which is defined as the ratio between the amplitude of the force transmitted to the base and that of excitation force is obtained in this section.

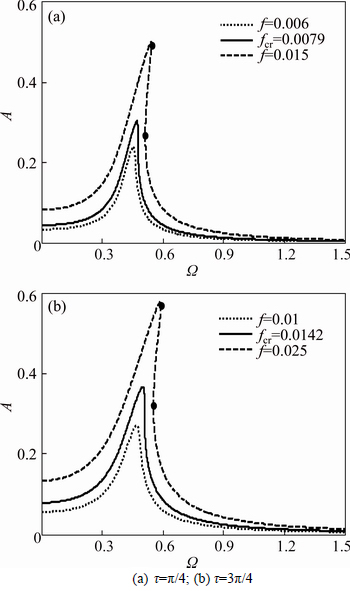
Fig. 12 Amplitude-frequency curves of controlled system for different excitation amplitude when u=0.02:

The force transmitted to the base is given as

                  (39)

The amplitude of the force can be obtained by substituting Eq. (15) into Eq. (39)

(40)

Then, the force transmissibility of the controlled HSLDS vibration isolator can be written in the form of decibel

  (41)

The effect of feedback gain on the force transmissibility is shown in Fig. 13. Interestingly, when the excitation amplitude is relatively large, the force transmissibility curve is discontinuous due to the fact that the restoring force is piecewise at discontinuity points. It can be seen that increasing the feedback gain can not only suppress the force transmissibility in resonant region but also reduce the resonance frequency. Furthermore, the bandwidth of vibration isolation also can be broadened. Though increasing the feedback gain could lead to the increase of force transmissibility in part of high frequency region, the adverse effect is still acceptable.

Fig. 13 Force transmissibility for various feedback gains when τ=π/4:

The effect of time delay on the force transmissibility is shown in Fig. 14. It can be seen that when there is no time delay, such feedback fails to suppress the force transmissibility in resonant region. As the time delay increases to τ=π/4, the force transmissibility in resonant region is suppressed remarkably. Besides, the resonance frequency also has an obvious reduction. When the time delay increases further to τ=π/2, the transmissibility curve becomes continuous and the effective frequency bandwidth of vibration isolation is broadened. Therefore, an appropriate choice of time delay is beneficial to the vibration control.

Fig. 14 Force transmissibility for various time delays when f=0.05, u=0.1

The aforementioned analysis in this section indicates that the feedback gain and time delay have obvious influence on the isolation performance of the controlled system. An appropriate choice of feedback parameters can not only broaden the frequency bandwidth of vibration isolation but also suppress the force transmissibility in resonant region, achieving a better isolation performance.

7 Conclusions

The linear displacement feedback is introduced in this paper to control the vibration of a HSLDS vibration isolator with piecewise nonlinear stiffness property. The primary resonance of the controlled system is obtained using the multiple scales method. The effects of feedback parameters, feedback gain and time delay, on primary resonance are studied from the viewpoint of equivalent damping. It is demonstrated that an appropriate time delay is beneficial to the vibration suppression. Besides, increasing the feedback gain can effectively suppress the response amplitude in resonant region. The jump avoidance condition is obtained subsequently.

The force transmissibility is defined to evaluate the isolation performance of the controlled HSLDS vibration isolator. The effects of feedback parameters on force transmissibility are then investigated and the results demonstrate that choosing an appropriate pair of feedback parameters can suppress the force transmissibility in resonant region and broaden the effective vibration isolation frequency bandwidth, achieving a better comprehensive performance.

References

[1] IBRAHIM R A. Recent advances in nonlinear passive vibration isolators [J]. Journal of Sound and Vibration, 2008, 314(3): 371–452.

[2] PLATUS D L. Negative-stiffness-mechanism vibration isolation systems [C]// Proceedings of SPIE-The International Society for Optical Engineering. Denver: International Society for Optical Engineering, 1999: 98–105.

[3] CARRELLA A, BRENNAN M J, WATERS T P. Static analysis of a passive vibration isolation with quasi zero-stiffness characteristic [J]. Journal of Sound and Vibration, 2007, 301(3): 678–689.

[4] CARRELLA A, BRENNAN M J, WATERS T P, LOPES J V. Force and displacement transmissibility of a nonlinear isolator with high-static-low-dynamic-stiffness [J]. International Journal of Mechanical Sciences, 2012, 55(1): 22–29.

[5] ROBERTSON W S, KIDNER M R F, CAZZOLATO B S, ZANDER A C. Theoretical design parameters for a quasi-zero stiffness magnetic spring for vibration isolation [J]. Journal of Sound and Vibration, 2009, 326(1, 2): 88–103.

[6] ZHOU N, LIU K. A tunable high-static low-dynamic stiffness vibration isolator [J]. Journal of Sound and Vibration, 2010, 329(9): 1254–1273.

[7] XU D L, YU Q P, ZHOU J X, BISHOP S R. Theoretical and experimental analyses of a nonlinear magnetic vibration isolator with quasi-zero-stiffness characteristic [J]. Journal of Sound and Vibration, 2013, 332(14): 3377–3389.

[8] LIU X T, HUANG X C, HUA H X. On the characteristics of a quasi-zero stiffness isolator using Euler buckled beam as negative stiffness corrector [J]. Journal of Sound and Vibration, 2013, 332(14): 3359–3376.

[9] HUANG X C, LIU X T, SUN J Y, ZHANG Z Y, HUA H X. Effect of the system imperfections on the dynamic response of a high-static-low-dynamic stiffness vibration isolator [J]. Nonlinear Dynamics, 2014, 76(2): 1157–1167.

[10] SHAW A D, NEILD S A, WAGG D J, WEAVER P M, CARRELLA A. A nonlinear spring mechanism incorporating a bistable composite plate for vibration isolation [J]. Journal of Sound and Vibration, 2013, 332(24): 6265–6275.

[11] ZHOU J X, WANG X L, XU D L, BISHOP S R. Nonlinear dynamic characteristics of a quasi-zero stiffness vibration isolator with cam-roller-spring mechanisms [J]. Journal of Sound and Vibration, 2015, 346: 53–69.

[12] CHENG C, LI S M, WANG Y, JIANG X X. On the analysis of a piecewise nonlinear-linear vibration isolator with high-static-low- dynamic-stiffness under base excitation [J]. Journal of Vibroengineering, 2015, 17(7): 3453–3470.

[13] HU H Y, DOWELL E H, VIRGIN L N. Resonances of a harmonically forced Duffing oscillator with time delay state feedback [J]. Nonlinear Dynamics, 1998, 15(4): 311–327.

[14] ELLIOTT S J, SERRAND M, GARDONIO P. Feedback stability limits for active isolation system with reactive and inertial actuators [J]. Journal of Vibration and Acoustics, 2001, 123(2): 250–261.

[15] LIU Y, WATERS T P, BRENNAN M J. A comparison of semi-active damping control strategies for vibration isolation of harmonic disturbances [J]. Journal of Sound and Vibration, 2005, 280(1, 2): 21–39.

[16] LI K A, XIAO H, CUI R F. Bifurcation control of nonlinear oscillator in primary and secondary resonance [J]. Journal of Central South University, 2007, 14(6): 826–831.

[17] GAO X, CHEN Q. Nonlinear analysis, design and vibration isolation for a bilinear system with time-delayed cubic velocity feedback [J]. Journal of Sound and Vibration, 2014, 333(6): 1562–1576.

[18] HUANG D M, XU W, XIE W X, HAN Q. Principle resonance response of a stochastic elastic impact oscillator under nonlinear delayed state feedback [J]. Chinese Physics B, 2015, 24(4): 040502.

[19] WANG Y, LI S M, CHENG C, JIANG X X. Dynamic analysis of a high-static-low-dynamic-stiffness vibration isolator with time- delayed feedback control [J]. Shock and Vibration, 2015, 2015: 1–19.

[20] SUN X T, XU J, JIN X J, CHENG L. Beneficial performance of a quasi-zero-stiffness vibration isolator with time-delayed active control [J]. International Journal of Mechanical Sciences, 2014, 82: 32–40.

[21] SCHMIDT G, TONDL A. Non-Linear Vibrations [M]. Cambridge: Cambridge University Press, 1986.

[22] JAZAR G N, HOUIM R, NARIMANI A, GOLNARAGHI M F. Frequency response and jump avoidance in a nonlinear passive engine mount [J]. Journal of Vibration and Control, 2006, 12(11): 1205–1237.

[23] JAZAR G N, MAHINFALAH M, DESHPANDE S. Design of a piecewise linear vibration isolator for jump avoidance [J]. Proceedings of the Institution of Mechanical Engineers, Part K: Journal of Multi-body Dynamics, 2007, 221(3): 441–449.

(Edited by HE Yun-bin)

Cite this article as: CHENG Chun, LI Shun-ming, WANG Yong, JIANG Xing-xing. Performance analysis of high-static-low-dynamic stiffness vibration isolator with time-delayed displacement feedback [J]. Journal of Central South University, 2017, 24(10): 2294–2305. DOI:https://doi.org/10.1007/s11771-017-3641-3.

Foundation item: Project(KYLX15_0256) supported by the Funding of Jiangsu Innovation Program for Graduate Education, China; Project(SV2015-KF-01) supported by the Open Project of State Key Laboratory for Strength and Vibration of Mechanical Structures, China; Project(XZA15003) supported by the Fundamental Research Funds for the Central Universities, China

Received date: 2016-03-18; Accepted date: 2016-07-08

Corresponding author: LI Shun-ming, Professor, PhD; Tel: +86–13605199671; E-mail: smli@nuaa.edu.cn