J. Cent. South Univ. (2019) 26: 98-105

DOI: https://doi.org/10.1007/s11771-019-3985-y

Application of composite nonlinear feedback control approach to linear and nonlinear systems

H Ebrahimi MOLLABASHI¹, A H MAZINAN¹, H HAMIDI²

1. Department of Control Engineering, Faculty of Electrical Engineering, South Tehran Branch,Islamic Azad University, Tehran 11365-4435, Iran;

2. Department of Information Technology Engineering, K. N.Toosi University of Technology,Tehran 16315-1355, Iran

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019

Abstract: The objective of this research is to realize a composite nonlinear feedback control approach for a class of linear and nonlinear systems with parallel-distributed compensation along with sliding mode control technique. The proposed composite nonlinear feedback control approach consists of two parts. In a word, the first part provides the stability of the closed-loop system and the fast convergence response, as long as the second one improves transient response. In this research, the genetic algorithm in line with the fuzzy logic is designed to calculate constant controller coefficients and optimize the control effort. The effectiveness of the proposed design is demonstrated by servo position control system and inverted pendulum system with DC motor simulation results.

Key words: composite nonlinear feedback; parallel-distributed compensation; sliding mode controller; optimization

Cite this article as: H Ebrahimi MOLLABASHI, A H MAZINAN, H HAMIDI. Application of composite nonlinear feedback control approach to a class of linear and nonlinear systems [J]. Journal of Central South University, 2019, 26(1): 98–105. DOI: https://doi.org/10.1007/s11771-019-3985-y.

1 Introduction

Desired transient performance of system is the most important subject in industrial applications. Overshoot and settling time of the system are two essential characteristics in the transient response. Contradiction between high performance and transient response is a serious problem in designing the controllers. Composite nonlinear feedback (CNF) approach is a simple and efficient technique, which is employed to overcome the contradiction of simultaneous achievement of the mentioned transient performance [1–3]. This technique stabilizes and enhances performance of the linear systems [4–6]. It should be noted that the CNF approach consists of two parts including a linear part and also a nonlinear part. The linear term leads to a closed-loop system with a small damping ratio such that the output response has a fast rise time. The main objective of the nonlinear part is the reduction and elimination of the overshoot in accordance with the linear feedback law. However, the aforementioned approach is applicable for single-input-single-output (SISO) systems. In all references, there is a compromise between the overshoot and settling time of response. Damping rate is assumed to be constant [7–10]. Value of the damping rate for the performance of various systems is investigated by EREN et al [11], an integral statement is added to CNF theory to eliminate the bias in a steady state by PENG et al [12], but disturbances and windup phenomenon were the main integral control problem. Over time, the CNF approach is implemented based on self-regulating HDD and helicopter systems. For a particular type of car suspension (MacPherson), a composite nonlinear feedback, with a layer and fuzzy rules, is used to reduce the chattering phenomenon [13, 14]. Implementation of a proportional-integral controller and evolutionary algorithms improved the error condition, gain and optimization in a study proposed by YAHAYA et al [15], where in this method, initial response search operations are investigated simultaneously from several points. The CNF technique with back-stepping method is proposed by FANG et al [16] for a steam generator, which is an important part of nuclear power plants.

Although, several contributions are made on the CNF idea to improve the transient performance, these approaches are only applicable for linear systems [1–16]. CNF technique is employed for a class of nonlinear discrete-time systems by HE et al [17], which comprised a zero-input globally asymptotically stable nonlinear system and constrained linear system. However, this class of limited structures could represent a few systems.

According to the survey, a few CNF methods have been applied to nonlinear systems. An adaptive fuzzy tracking control is applied to single input single output (SISO) nonlinear systems with non-strict feedback by WANG et al [18], but this class of systems are limited. Therefore, in this investigation, Takagi-Sugeno (T-S) fuzzy model- based on controllers have been proposed for nonlinear systems. One of the main advantages of T-S fuzzy systems is that they prove universal approximates and can exactly describe the original nonlinear system with convex structure [19–23]. Another advantage of the T-S fuzzy model is its compatibility with the linear matrix inequality (LMI) [24–26]. Usually, parallel-distributed compensation (PDC) scheme is used for such fuzzy control configuration [26]. PDC control comprises several linear controllers, which are compatible with the fuzzy techniques. In this research, a CNF based on sliding mode controller is designed to deal with the linear systems. Then, fuzzy logic is employed, in order to optimize and reduce error. After that, CNF based on PDC is applied to nonlinear systems described by the aforementioned T-S fuzzy models. The proposed CNF technique in this paper is applicable to handle large class of linear and nonlinear systems. Finally, to show the merits of the proposed approach, it is applied to an inverted pendulum system with DC motor and servo position control system, as well.

The rest of this paper is organized as follows: The problem description is presented in Section 2. Simulations are all illustrated in Section 3 and finally, the results are concluded in Section 4.

2 Problem description

In this section, the composite nonlinear feedback control law is studied for linear and nonlinear systems. First part presents the proposed CNF controller including the sliding mode controller, while the second part also presents the CNF controller including the parallel-distributed compensation (PDC) with T-S fuzzy model for nonlinear systems.

2.1 CNF strategy for linear systems

The equation of nominal plant with the uncertainty can now be given as [9]:

         (1)

where x is the state vector; u is the control input vector; y is the output vector; A, B and C are the matrixes of appropriate dimensions; △f(x) represents the system uncertainties and |△f(x)|≤△f(x)_max where △f(x)_max is the maximum amplitude of disturbance.

CNF strategy for linear systems is given by:

u_CNF=u_SMC+u_MOD                         (2)

2.1.1 Sliding mode control (SMC)

In this section, we design sliding mode control to provide robust closed loop performance. To guarantee the stability of the closed-loop, the SMC controller is utilized. The sliding surface function is utilized as:

     (3)

where ψ(x, t)≥△f(x)_max is taken as a gain related to the maximum bound of disturbances.

2.1.2 Modified term

A modified term is added to the SMC controllers to decrease the overshoot of the system response. This term is defined as follows [3]:

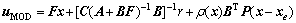 (4)

where ρ(x)≤0 is an arbitrary non-positive scalar and P=P^T>0 is a symmetric positive definite matrix with appropriate dimensions and it is obtained as the solution to the Lyapunov equation V=x^TPx. r is the tracking target. F is the linear feedback gain and required to make (A+BF) asymptotically stable. Fuzzy logic can be used in order to calculate this parameter. Several choices can be considered for the structure of ρ(x). One common choice for the single output systems is selecting of exponential function as follows [8]:

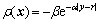                          (5)

where y is the value of system output; α and β≥0 are tuning parameters calculated by genetic algorithm. The nonlinear function varies from 0 to –β. Initially, at t=0 and when the system output is far away from its equilibrium point the value of ρ(x) is near zero. Therefore, the modified term has a small effect on the control input.

2.1.3 Optimal control problem

There are many approaches to achieve the desired tracking performance to the close-loop system, such as, H₂ or H_∞ approaches etc. In this research, the genetic algorithm (GA) and fuzzy logic is used to calculate fixed parameters and optimize the time response. In the fuzzy logic system, singleton function, center average defuzzification and product inference are assumed. To evaluate the constant value of controller, the cost function is now shown as formula (6). Cost function that is used in GA is considered by a Quadratic finite-time integral performance index as follows:

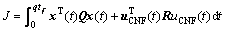        (6)

where q is appositive integer; t_f denotes a small time integral; Q is a symmetric positive-semi definite matrix and R is asymmetric positive-definite matrix.

2.2 CNF strategy for nonlinear systems

In this part, a CNF controller based on T-S fuzzy model is proposed. This control law comprises two nonlinear terms. The first term is constructed based on the PDC. The second term, that we called it the modified term, is a nonlinear function with special properties. The structure of T-S fuzzy model with PDC is shown in Figure 1.

The T-S fuzzy model is fuzzy aggregation of finite and definite number of fuzzy rules whose consequent parts comprise locally linear state-space representation of the original nonlinear system. The T-S fuzzy model with singleton fuzzification and center average defuzzification is as follows:

  (7)

where w_i is the weight in its corresponding membership function. Furthermore, r denotes the number of fuzzy rules,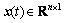and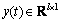 are system state vector and system output vector respectively,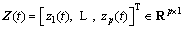is the fuzzy premise variable vector.

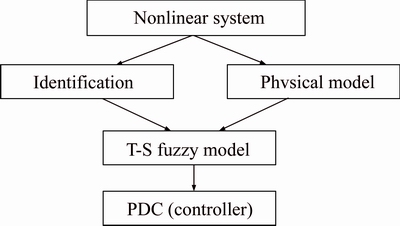
Figure 1 T-S fuzzy model with PDC

2.2.1 PDC Controller

One approach to control T–S fuzzy system is the PDC method. In this method, the output of fuzzy controller has the same rules as its T–S fuzzy model. In addition, the T-S fuzzy model and the PDC controller have the same premise variable and fuzzy membership functions. The overall fuzzy controller system is of the following form:

         (8)

In this equation is local feedback gain of PDC controller, which will be designed, in the forthcoming lemma 1.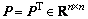is symmetric positive-definite Lyapunov matrix.

2.2.2 Modified term

In addition, a modified term is added to the PDC controller to decrease the overshoot of the system response. This term is defined as follows:

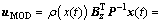
            (9)

whereis an arbitrary non-positive nonlinear scalar. Several choices can be considered for structure of ρ(x(t)). One common choice for the single output systems is selecting of exponential function as follows [8]:

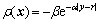                         (10)

Therefore, the control input is influenced significantly by the modified term. The overall proposed CNF controller will be:

u_CNF=u_PDC+u_MOD                         (11)

To derive the sufficient conditions of the PDC controller design in terms of LMIs, first we reformulate the open-loop T-S system. Such that the hard input nonlinearity is eliminated and the new system has unconstrained control input with additional term including the nonlinearity terms. To achieve this goal null term is added.

             (12)

The T-S fuzzy system can be re-written as follows:

               (13)

whereSubstituting the PDC controller into the open-loop T-S system, the closed-loop T-S fuzzy system is obtained as follows:

           (14)

Lemma 1 [23]: For the given scalars τ₁≥0 and ρ≥0, the stability of the closed-loop system (14) is guaranteed for the region R(ρ, P)= if exist. The symmetric positive definite matrix P and the matrices F_i for i=1, …, r such that the following LMIs hold:

Q_ii<0 for i≠j , i=1, 2, …, r                 (15)

 (16)

where is the k-th row of the matrix F_i. CHIANG et al [24] prove that if the LMI conditions (15) lead to feasible solutions then, the stability of the closed-loop system with input saturation constraint will be guaranteed and the matrices P and F are computed.

3 Simulations

Two examples are given to illustrate the advantages of the proposed approach. In the first example, linear model of servo position control system is presented. In order to optimize and calculate the constant value, the fuzzy logic and the genetic algorithm are realized. In the second example, an inverted pendulum system with DC motor is considered. Furthermore, the equivalent T-S fuzzy model of the system is derived. Finally, the proposed CNF controller is applied and the obtaining results are compared with those obtained from research by NAMAZOV et al [27] in which PDC controller is designed.

Example 1: The servo position control system with disturbance is considered as follows:

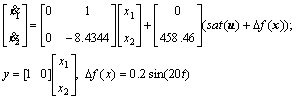
where x₁, x₂, u and d are respectively taken as the angular position of the load disc, the angular velocity, the input voltage and disturbance. In addition, the reference step signal to be tracked is r=50. In the simulation, the membership functions are chosen as Figure 2, Figure 3 shows the sliding surfaces. According to this control approach, the sliding surface is asymptotically stable.

Figures 4 and 5 show the tracking performance of the closed-loop system for the position and angular velocity respectively. It is found that the servo position control system can be stabilized to the equilibrium point. It can be observed that the CNF controllers achieve much higher tracking performance in the presence of disturbance. Finally, Figure 6 illustrates the CNF control input.

Example 2 [27]: To show the effectiveness of the proposed approach, we consider the inverted pendulum system with DC motor, as follows:

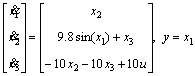           (17)

Figure 2 Membership functions for F function:

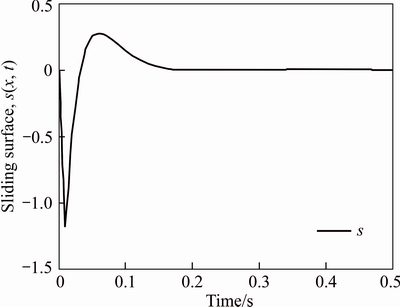
Figure 3 Sliding surface

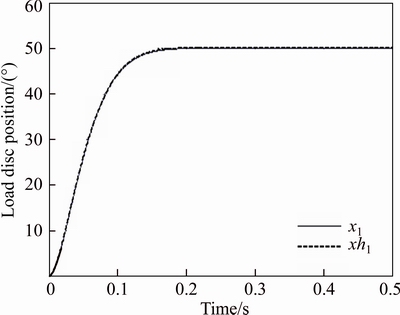
Figure 4 Angular position of load disc (x₁)

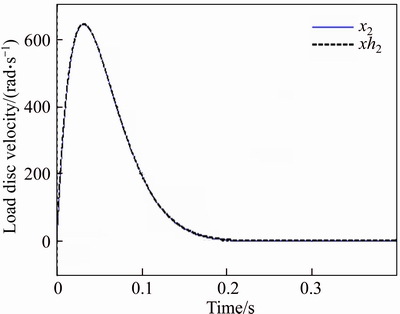
Figure 5 Angular velocity (x₂)

Figure 6 Control input (u)

By applying the sector nonlinearity approach for the region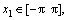state matrix can be defined as follows:

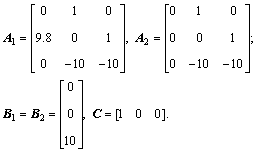
By applying lemma 1 with ε=0.7 and ρ=10, the following LMI variables and PDC controller gains are computed:

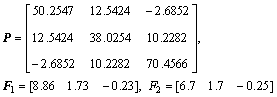 (18)

By genetic algorithm tools, the design parameters are considered as β=8.9 and γ=0.01. To illustrate the advantage of the proposed approach (CNF-PDC) in improving the closed-loop transient performance, the PDC controller is considered for comparing the results [27]. Simulations are carried out by the initial condition x(0)=[2 0 0]. The closed-loop inverted pendulum system with DC motor states are illustrated in Figure 7; the proposed approach can effectively stabilize the closed-loop system and improve the transient performance. It is concluded that the proposed approach CNF controller reduces the overshoot in the system response.

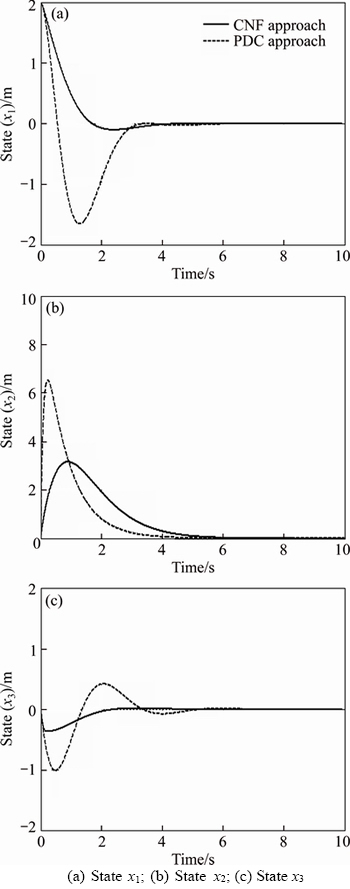
Figure 7 Closed-loop state variable of inverted pendulum system with DC motor:

As it can be seen in Figure 7, the results are compared quantitatively. The overshoot of the closed-loop system states in Table 1 reveals that the proposed approach provides favorable transient performance.

Table 1 Overshoot of states of inverted pendulum system with DC motor

4 Conclusions

A new approach for transient improvement of linear and nonlinear closed-loop systems is proposed in this investigation. This approach can be applied to linear and nonlinear systems directly. In the nonlinear systems, the PDC-CNF controller is applied to TS fuzzy model and numerical optimization (LMI) technique is used for stabilization. In the linear system, the SMC-CNF controller is designed to deal with the linear model and fuzzy logic and genetic algorithms are realized for optimization and calculation of constant value of CNF and sliding mode surfaces. Finally, in order to show the merits of the proposed approach, it is applied to a servo position control system and an inverted pendulum system with DC motor. Simulations results demonstrate that the CNF strategy reduces overshoot very faster than the existing methods in hand. Singular systems, hybrid systems, alternative control methods and nonlinear sliding surfaces based on sliding mode controller are all suggested for the future researches.In a word, for these future works, the proposed approach can be verified via a series of experiments.

References

[1] LI Y, TONG SH, LI T I. Composite adaptive fuzzy output feedback control design for uncertain nonlinear strict-feedback systems with input saturation [J]. IEEE Transactions on Cybernetics, 2015, 45(10): 2299–2308. DOI: 10.1109/TCYB.2014.2370645.

[2] TONG S H, LI Y, SUI S H. Adaptive fuzzy tracking control design for SISO uncertain non-strict feedback nonlinear systems [J]. IEEE Transactions on Fuzzy Systems, 2016, 24(6): 1441–1454. DOI: 10.1109/TFUZZ.2016.2540058.

[3] ZHANG B, LAN W. Improving transient performance for output regulation problem of linear systems with input saturation [J]. Int J Control, 2014, 23(10): 1087–1098. DOI: 10.1002/rnc.2941.

[4] WANG R, HU C, YAN F, CHADLI M. Composite nonlinear feedback control for path following of four-wheel independently actuated autonomous ground vehicles [J]. IEEE Trans Intell Transp Syst, 2016, 17(7): 2063–2074. DOI: 10.1109/TITS.2015.2498172.

[5] WANG C H, CHU X I, LAN W E. Composite nonlinear feedback control for output regulation problem of linear discrete-time systems with input saturation [J]. Journal of Systems Engineering and Electronics, 2014, 25(6): 258–263. DOI: 10.1109/JSEE.2014.00120.

[6] THUM C K, DU C L, CHEN B M, ONG E H, TAN K P. A unified control scheme for track seeking and following of a hard disk drive servo system [J]. IEEE Trans Control Syst Technol, 2010, 18(2): 294–306. DOI: 10.1109/TCST.2009. 2017513.

[7] FENG Y, HO D W C. Transient performance for discrete-time singular systems with actuators saturation via composite nonlinear feedback control [J]. Int J Robust Nonlinear Control, 2014, 24(5): 955–967. DOI: 10.1002/ rnc.2930

[8] HU C, WANG R, YAN F, CHEN N. Robust composite nonlinear feedback path-following control for underactuated surface vessels with desired-heading amendment [J]. IEEE Trans Ind Electron, 2016, 63(10): 6386–6394. DOI: 10.1109/TIE.2016.2573240.

[9] HE Y, CHEN B M, WU C. Composite nonlinear control with state and measurement feedback for general multivariable systems with input saturation [J]. Syst Control Lett, 2005 54(5): 455–469. DOI: 10.1016/j.sysconle.2004.09.010.

[10] CHENG G, PENG K, CHEN B M, LEE T H. Improving transient performance in tracking general references using composite nonlinear feedback control and its application to high-speed XY-Table positioning mechanis [J]. IEEE Transactions on Industrial Electronics, 2007, 54(2): 1039–1051. DOI: 10.1109/TIE. 2007.892635

[11] EREN S, PAHLEVANINEZHAD M, BAKHSHAI A, JAIN P. Composite nonlinear feedback control and stability analysis of a grid-connected voltage source inverter with LCL filter [J]. IEEE Transactions on Industrial Electronics, 2012, 60(11): 5059–5074. DOI: 10.1109/TIE.2012.2225399.

[12] PENG K, CHEN B M, CHENG G, LEE T H. Modeling and compensation of nonlinearities and friction in a micro hard disk drive servo system with nonlinear feedback control [J]. IEEE Transactions on Control Systems Technology, 2005, 13: 708–721. DOI: 10.1109/TCST.2005.854321.

[13] LAN W, THUM C K, CHEN B M. A hard-disk-drive servo system design using composite nonlinear feedback control with optimal nonlinear gain tuning methods [J]. IEEE Transactions on Industrial Elecronics, 2010, 57: 1735–1745. DOI: 10.1109/TIE.2009.2032205.

[14] NIKDEL P, HOSSEINPOUR M, BADAMCHIZADEH M A, AKBARI M A. Improved Takagi–Sugeno fuzzy model-based control of flexible joint robot via Hybrid-Taguchi genetic algorithm [J]. Engineering Applications of Artificial Intelligence, 2014, 33: 12–20. DOI: 10.1016/j.engappai. 2014.03.009.

[15] YAHAYA M D, SHAHDAN S, LIYANA R, KHAIRI M, GHAZALI R. A reduce chattering problem using composite nonlinear feedback and proportional integral sliding mode control [C]// IEEE International Control Conference Asian. 2015: 1–6. DOI: 10.1109/ASCC.2015.7244566.

[16] FANG F, SHI Y. Adaptive back-stepping-based composite nonlinear feedback water level control for the nuclear U-Tube steam generator [J]. IEEE Transactions on Control Systems Technology, 2014, 22: 369–377. DOI: 10.1109/ TCST.2013.2250504.

[17] HE Y, CHEN B M, LAN W. On improving transient performance in tracking control for a class of nonlinear discrete-time systems with input saturation [J]. IEEE Trans on Autom Control, 2007, 52(7): 1307–1313. DOI: 10.1109/ TAC.2007.900836.

[18] WANG T, ZHANG Y F, QIU J B, GAO H J. Adaptive fuzzy backstepping control for a class of nonlinear systems with sampled and delayed measurements [J]. IEEE Transactions on Fuzzy Systems, 2015, 23(2): 302–312. DOI: 10.1109/ TFUZZ.2014.2312026.

[19] KHOOBAN M H, VAFAMAND N, DRAGICEVIC T, BLAABJERG F, NIKNAM T. Model predictive control based on T-S fuzzy model for electrical vehicles delayed model [J]. IET Electr Power Appl, 2016, 64: 231–240. DOI: 10.1016/j.isatra.2016.04.019.

[20] LILLY H J. Fuzzy control and identification [M]. New York: Wiley, 2010.

[21] MRQUEZ R, GUERRA T M, BERNAL M, KRUSZEWSKI A. A non-quadratic Lyapunov functional for H_∞ control of nonlinear systems via Takagi–Sugeno models [J]. J Frankl Inst, 2016, 353(4): 781–796. DOI: 10.1016/ j.jfranklin.2016.01.004.

[22] GUERRA T M, ESTRADA-MANZO V, LENDEK Z. Observer design for Takagi–Sugeno descriptor models: An LMI approach [J]. Automatica, 2015, 52: 154–159. DOI: 10.1016/j.automatica.2014.11.008.

[23] VAFAMAND N, ASEMANI M H, KHAYATIYAN A. A robust L1 controller design for continuous-time TS systems with persistent bounded disturbance and actuator saturation [J]. Eng Appl Artif Intell, 2016, 56: 212–221. DOI: 10.1016/j.engappai.2016.09.002.

[24] CHIANG T, LIU P. Robust output tracking control for discrete-time nonlinear systems with timevarying delay: Virtual fuzzy model LMI-based approach [J]. Expert Systems with Applications, 2012, 39: 8239–8247. DOI: 10.1016/ j.eswa.2012.01.163.

[25] VAFAMAND N, SHASADEGHI M. More relaxed non-quadratic stabilization conditions for TS fuzzy control systems using LMI and GEVP [J]. Int J Control Autom Syst, 2015, 13(4): 995–1002. DOI: 10.1007/s12555-013-0497-7.

[26] TANAKA K. Fuzzy control systems design and analysis: A linear matrix inequality approach [M]. New York: Wiley, 2001.

[27] NAMAZOV M, TEKGUN B, CELIKKALE E. Design of a stable takagi-sugeno fuzzy control system via LMIs with disturbance rejection [C]// IEEE International Symposium on Innovations in Intelligent Systems and Application (INISTA). IEEE, 2012: 950–956. DOI: 10.1109/INISTA.2012.6246945.

(Edited by HE Yun-bin)

中文导读

复合非线性反馈控制方法在线性和非线性系统中的应用

摘要：针对一类具有平行分布补偿的线性和非线性系统，采用滑模控制技术，实现了一种复合非线性反馈控制方法。所提出的复合非线性反馈控制方法由两部分组成。第一部分给出了闭环系统的稳定性和快速收敛响应，而第二部分改进了瞬态响应。本研究设计了符合模糊逻辑的遗传算法来计算常系数和优化控制效果。通过伺服位置控制系统和倒立摆系统的仿真，验证了所提设计的有效性。

关键词：复合非线性反馈；并行分布补偿；滑模控制器；优化

Received date: 2017-10-26; Accepted date: 2018-04-11

Corresponding author: A H MAZINAN, PhD; Tel: +98-21-33722831; E-mail: mazinan@azad.ac.ir; ORCID: 0000-0002-8810-9574