采用分量均值正交分割法设计矢量量化初始码书
邓宏贵,郭晟伟
(中南大学 物理科学与技术学院,湖南 长沙,410083)
摘 要:提出一种新的矢量量化初始码书设计算法即分量均值正交分割法。其原理是:利用分量均值对样本空间进行正交分割,使初始码字尽量散开,得到充分利用。研究结果表明:分量均值正交分割法在不同图像、不同码书下,与随机法相比,峰值信噪比提高1.0~1.3 dB,训练时间增加不超过30%;与分裂法相比,峰值信噪比相差小于0.1 dB,训练速度提高1.0~1.5倍;与其他算法相比,在量化失真和训练速度2个相互冲突的指标之间能取得更好的均衡。
关键词:矢量量化;初始码书;分量均值;正交分割
中图分类号:TN911.73 文献标志码:A 文章编号:1672-7207(2010)02-0628-04
Initial codebook of vector quantization designed by
component mean orthogonal segmentation
DENG Hong-gui, GUO Sheng-wei
(School of Physics Science and Technology, Central South University, Changsha 410083, China)
Abstract: A new algorithm component mean orthogonal segmentation algorithm (CMOSA) was proposed to generate vector quantization initial codebook using component mean. The results show that in different images and different codebook sizes, compared with random algorithm, peak signal to noise ratio rises by 1.0-1.3 dB, and training time increases no more than 30%. Compared with splitting algorithm, peak signal to noise ratio difference is less than 0.1 dB, but the training speed improves 1.0-1.5 times. Between training speed and quantization distortion of the two conflicting indicators, CMOSA achieves a better balance than other algorithms.
Key words: vector quantization; initial codebook; component mean; orthogonal segmentation
矢量量化(Vector quantization, VQ)[1]技术是一种高效的数据压缩技术,由于其可以获得比标量量化更高的压缩比,故广泛应用于语音、图像和视频压缩系统。码书设计是矢量量化最关键的技术,直接影响到量化系统的性能。Linde等[2]提出的LBG算法物理含义清晰,数学推理严密,易于实现。但是,LBG算法严重依赖初始码书的选择,直接影响训练算法的收敛速度和码书质量。目前,初始码书有3种生成方法,即随机法、分裂法(Splitting algorithm, SA)[3-5]和乘积码书法。随机法就是从N个训练矢量中随机抽取M个作为初始码书。这种方法简单易行,且不会出现空胞腔,但结果具有较大偶然性。分裂法是首先把整个训练样本看成1个胞腔,再用最优分割超平面将胞腔一分为二,二分为四,直到形成M个胞腔,以这些胞腔的质心得到M个码字。采用该法量化失真小,但是,多维最优分割超平面的选择是一个非常复杂的问题[6]。乘积码书法以若干低维的码书作为乘积码,再求得高维码书,计算量小,但性能差。不同的初始码书会使LBG 迭代算法陷入不同的局部最优解。目前,虽然人们对全局最优解进行了研究[7-9],但计算量均很大。事实上,使初始码字根据样本分布规律尽量散开可以得到更好的迭代解[10-11]。在此,本文作者利用矢量在各个维度上的分量均值这一统计特性,将码书尽量散开得到充分利用,以便得到比以往算法更优的码书。
1 传统LBG算法
将N个输入矢量用M个码字矢量来量化,实际上是一个聚类问题,目前,没有多项式法求全局最优码书(均方量化误差最小的码书)。经典的LBG算法是基于最佳划分和最佳码字[12]这2个必要条件提出来的,采用迭代方法求得局部最优解。其算法步骤如下。
步骤1:初始化,给定训练矢量集T={xi|xi∈Rk, 1≤i≤N},码书大小为M,迭代门限ε>0,初始码书为C(0),置迭代次数t=0,初始失真D(-1)=∞。
步骤2:依据最近邻法则[13]将T划分为M个Voronoi胞腔。
步骤3:计算平均量化失真
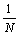 ?
? 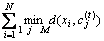 。若失真下降率为(D(t-1) -D(t))/D(t)
。若失真下降率为(D(t-1) -D(t))/D(t)
≤ε,则停止算法,码书C(t)就是所求的码书,否则转下一步。
步骤4:将M个胞腔的质心作为新码书,t=t+1,返回步骤2。
从以上步骤可以看出:LBG算法初始码书的选择至关重要,它影响到算法的收敛速度和最终码书的性能。传统初始码书生成方法一般采用随机法和分裂法,其中:随机法性能差,分裂法计算量大且性能有待提高[5]。本文从分量均值这一特征值出发,提出一种新的初始码书生成算法即分量均值正交分割法(Component mean orthogonal segmentation algorithm, CMOSA)。
2 分量均值正交分割法
2.1 基本思想
先引出2个与本文算法密切相关的概念——矢量均值和分量均值。
设x为Rk空间的k维矢量,xj(1≤j≤k)表示x在第j个维度的投影,矢量x的均值μx定义为:
 (1)
(1)
本文将其简记为矢量均值。
设xi(1≤i≤N)为Rk空间N个k维矢量,这N个矢量组成1个矢量组,xij(1≤i≤N, 1≤j≤k)表示矢量xi在第j个维度的投影。矢量组第j维分量的均值定义为:
 , 1≤j≤k (2)
, 1≤j≤k (2)
本文简记为分量均值。
引入如下定义:设L为Rk空间的1条直线,若L上任意点p=(p1, p2, …, pk)都满足p1=p2=…= pk,则称L为Rk的中心线[14]。
从物理意义上看,矢量x的矢量均值相当于矢量x在冗余维度xL=(x1+x1+…+xk)/k上的投影。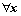 ∈Rk,x在L上的投影点为px=(μx, μx, …, μx)。因此,与L正交的超平面上的所有点矢量均值相等,称为等均值超平面。
∈Rk,x在L上的投影点为px=(μx, μx, …, μx)。因此,与L正交的超平面上的所有点矢量均值相等,称为等均值超平面。
码书通常是以矢量均值划分样本空间,这样会出现1个问题:即使划分非常细,胞腔空间也是由2个无限宽的平行等均值超平面包裹,仍然存在欧式距离很大的码字同属一个胞腔的问题,而且矢量均值计算量大。该矢量均值仅仅是xL维度上的投影所致。这种方法只利用了训练样本在xL维度上的分布特点,而没有利用在其他维度上的分布特点,因而,不如直接依次用各分量空间的均值分割。这种在各个维度上都对训练样本空间进行分割的方法,使分割平面相互正 交,由于每次分割只涉及1个相异的独立维度,计算量小,且同一胞腔内码字之间欧式距离小。根据这种情况,本文提出了基于分量均值分割的初始码书设计新算法。
2.2 实现步骤
假设有N个k维训练样本,码书大小为M,本文算法先计算N个训练样本在x1维度的均值μ1,利用该均值将样本空间一分为二,再将失真大的区域在x2维度作正交分割共得到3个区域,依此类推,最终得到M个区域。以这些区域的质心作为初始码书,可以保证码字尽量散开,得到充分利用。新算法的实现步骤如下。
步骤1:初始化。给定训练矢量集T={xi|xi∈Rk, 1≤i≤N},最终码书大小为M,开始时所有训练矢量组成一个区域S1,置初始维度j=1,初始码字个数m=1,初始最大失真区域序号v=1。
步骤2:按照式(2)计算最大失真区域Sv在维度j上的分量均值μj。使用μj将区域Sv一分为二,即Sm+1和Sm+2。
Sm+1={x|xj≥μj, x∈Sv}, Sm+2={x|xj≥μj, x∈Sv} (3)
去掉Sv,以Sm+2代替Sv,保证区域个数增加1。若j=k,则j=1,否则j=j+1,m=m+1;若m=M,则结束分割,转步骤4。
步骤3:分别计算m个区域的平均量化失真Dt,找出失真最大的区域,即
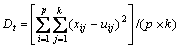 , 1≤t≤m (4)
, 1≤t≤m (4)
式中:p为区域St内样本个数。找出其中平均量化失真最大的区域序号v, ,转步骤2。
,转步骤2。
步骤4:分别计算M个区域的质心,作为初始码书赋给LBG算法进行迭代。
该算法利用分量均值正交分割平均失真最大的区域,直至形成需要的M个初始胞腔,以分割后的区域质心作为初始码书放到LBG算法迭代。需要说明的是:按照这些步骤获得的初始码书不是最优码书。本方法的目的只是为LBG算法提供大致按照训练样本规律分布的初始码字,使初始码字得到充分利用。
2.3 非均匀分布样本改进措施
从上述基本思想和实现步骤可以看出:分量均值正交分割设计法对于均匀分布的样本特别有效。实际上,大多数图像样本都不是完全地均匀分布,这样,对某一区域分割时,若少数几个样本在维度xj上与其他样本差别很大,则可能出现非典型码字(映射到该码字的样本数目很少),这些码字利用率不高。由于该算法以分量均值分割,每个新区域至少包含1个样本,因此,不可能出现空胞腔,至多出现非典型码字。为了解决该算法的非典型码字问题,需要对步骤2略加改进,具体方法如下。
对于分割得到的2个新胞腔,统计其中样本数pi (i为m+1和m+2)。若pi小于预先设定的非典型码字门限Ns,则认定该码字为非典型码字,去掉区域Si,将其中样本划分给其他最临近的码字所属胞腔。这样,本次操作相当于只对离中心码字较远的部分样本进行调整,而不增加胞腔个数。参数Ns一般是训练样本规模N的弱函数,Ns 随着N增大而略增大,经验值取3~5为宜。
经过改进之后,本文的分量均值正交分割法对于非均匀分布样本同样适用,应用范围扩大。
3 算法仿真及结果讨论
实验硬件环境:CPU(P4 2.93 G),内存为512 M,DDR;实验软件环境:Visual C++ 6.0。
从标准测试图像库中选取10幅大小为256×256和256色的灰度图像进行测试。将图像划为4×4的小块,因此,矢量维数k=16,样本数N=4 096,码书大小M∈{8,16,32,64,128,256,512,1 024},失真下降门限ε取0.001。分别用LBG算法[2]、SA+LBG算法[15]、本文算法进行码书设计,把各种方法在不同码书下的失真度和训练时间这2个最重要的参数进行对比。其中,训练时间包括初始码书设计时间和迭代优化时间,失真度用峰值信噪比RPSN度量。
设原始像素为xij,量化值为qij,均方误差EMS、峰值信噪比RPSN定义为:

选取最典型的Lena和Barb 2幅图像,在码书大小为128时进行对比,结果见表1。图1所示为3种算法在不同码书大小下失真度的对比结果;图2所示为不同码书大小下训练时间对比结果。实验结果表明:本文提出的分量均值正交分割法与经典LBG算法相比,峰值信噪比RPSN提高超过1 dB,训练时间增加不超过30%;相对于SA+LBG法,RPSN相差不超过0.1 dB,但训练速度提高了1.0~1.5倍。其原因是:以随机方式产生初始码书的LBG算法,不需要附加计算,耗时最少。但是,由于初始码字不能自适应于训练样本的统计特性,最终收敛到RPSN较低的局部最优解。用SA产生初始码书,可以使初始胞腔沿着失真下降最大的方向分裂,产生较好码书,但是,在分裂过程中,寻找最优分割超平面需进行繁琐的运算,算法应用受到限制。本文提出的CMOSA算法,充分利用了正交分割平均失真最大的胞腔,使初始码字尽量散开,再在LBG算法中迭代,最终码书质量比随机LBG的质量高得多,与SA和LBG联合算法相比码书质量相
表1 Lena和Barb图像在3种算法下的性能对比(M=128)
Table 1 Performance comparison of three algorithms for Lena and Barb images (M=128)

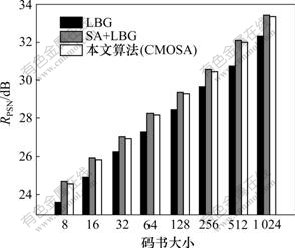
图1 3种算法的RPSN对比
Fig.1 Comparison of peak signal to noise ratio of three algorithms

1—LBG; 2—SA+LBG; 3—本文算法(CMOSA)
图2 3种算法训练时间对比
Fig.2 Training time comparison of three algorithms
差很小。由于CMOSA算法只需M次分量均值的计算,相对于分裂法M次分裂[6]少得多,故比SA和LBG联合算法的运算速率快得多。
4 结论
(1) 基于分量均值正交分割平均失真最大的胞腔,提出了一种矢量量化初始码书设计算法即CMOSA算法。
(2) CMOSA算法量化误差小。与经典LBG算法相比,CMOSA算法峰值信噪比提高超过1 dB;与SA和LBG联合算法相比,峰值信噪比相差低于0.1 dB。
(3) CMOSA算法运算量小。CMOSA算法与经典LBG算法相比,训练时间增加不超过30%;与SA和LBG联合算法相比,训练速度提高1.0~1.5倍。
参考文献:
[1] Gersho A, Gray R M. Vector quantization and signal compression[M]. Boston: Kluwer Academic Publishers, 1992.
[2] Linde Y, Buzo A, Gray R M. An algorithm for vector quantizer design[J]. IEEE Transactions on Communications, 1980, 28(1): 84-95.
[3] Lee W F, Chan C K. Two-dimensional split and merge algorithm for differential vector quantization of images[J]. Image Communication, 1998, 13(1): 1-14.
[4] Stephen S, Kuldip K P. Efficient product code vector quantisation using the switched split vector quantiser[J]. Digital Signal Processing, 2007, 17(1): 138-171.
[5] Ahmed M E. Fast methods for split codebooks[J]. Signal Processing, 2000, 80(12): 2553-2565.
[6] Chan C K, Ma C K. A fast method of designing better codebooks for image vector quantization[J]. IEEE Transactions on Communications, 1994, 42(234): 237-242.
[7] Franti P. Genetic algorithm with deterministic crossover for vector quantization[J]. Pattern Recognition Letters, 2000, 21: 61-68.
[8] 李霞, 罗雪晖, 张基宏. 基于人工蚁群优化的矢量量化码书设计算法[J]. 电子学报, 2004, 32(7): 1082-1085.
LI Xia, LUO Xue-hui, ZHANG Ji-hong. Codebook design for image vector quantization with ant colony optimization[J]. Acta Electronica Sinica, 2004, 32(7): 1082-1085.
[9] 陆哲明, 潘正祥, 孙圣和. 基于改进禁止搜索算法的矢量量化码书设计[J]. 电子学报, 2000, 28(9): 108-110.
LU Zhe-ming, PAN Zheng-xiang, SUN Sheng-he. VQ codebook design based on the modified tabu search algorithms[J]. Acta Electronica Sinica, 2000, 28(9): 108-110.
[10] Villmann T, Schleif F, Hammer B. Comparison of relevance learning vector quantization with other metric adaptive classification methods[J]. Neural Networks, 2006, 19(5): 610-622.
[11] Shen F, Hasegawa O. An adaptive incremental LBG for vector quantization[J]. Neural Networks, 2006, 19(5): 694-704.
[12] Lloyd S. Least squares quantization in PCM[J]. IEEE Transactions on Information Theory, 1982, 28(2): 129-137.
[13] Garey M R, Johnson D S, Witsenhausen H S. The complexity of the generalized Loyd-Max problem[J]. IEEE Transactions on Information Theory, 1982, 28(2): 255-256.
[14] Ra S W, Kim J K. Fast mean-distance-ordered partial codebook search algorithm for image vector quantization[J]. IEEE Transactions on Circuits and Systems-II, 1993, 40(9): 576-579.
[15] 李弼程, 文超, 平西建. 两个优于分裂法的初始码书设计算法[J]. 中国图像图形学报, 2000, 5(1): 48-51.
LI Bi-cheng, WEN Chao, PING Xi-jian. On the design of original codebooks with two algorithms better than the splitting algorithm[J]. Journal of Image and Graphics, 2000, 5(1): 48-51.
收稿日期:2009-02-10;修回日期:2009-05-03
基金项目:国家自然科学基金资助项目(60672041);国家高技术研究发展计划(“863”计划)子课题(E20050605)
通信作者:邓宏贵(1965-),男,湖南长沙人,博士,教授,从事智能控制和信息处理研究;电话:0731-88836424;E-mail: denghonggui@163.com
(编辑 陈灿华)