Al-Si合金宏观偏析、凝固组织演变的元胞自动机-控制容积法耦合模拟
来源期刊:中国有色金属学报2012年第7期
论文作者:张红伟 NAKAJIMA Keiji 王恩刚 赫冀成
文章页码:1883 - 1896
关键词:Al-Si合金;凝固;晶体生长;宏观偏析;元胞自动机-控制容积积分法
Key words:Al-Si alloy; solidification; grain growth; macrosegregation; cellular automaton-finite volume method
摘 要:建立凝固过程中宏观流动、传热、溶质传输与微观形核、生长过程双向耦合数学模型,并针对Al-Si二元合金凝固过程进行二维元胞自动机-控制容积积分法(CA-FV)耦合模拟。模型反映了流场下晶体逆流生长特性,考虑了温降导致的形核和生长以及形核和生长引起的固相分率变化对宏观场的影响,能预测凝固过程中再辉和晶间偏析等现象,反映合金液流动对合金的溶质分布以及凝固组织形貌的作用规律。与仅宏观传输模拟结果和无流动影响的模拟结果进行了对比,验证了耦合模型的优越性。同时考察了铸型尺寸对凝固组织形貌的影响。
Abstract: A coupled cellular automaton-finite volume (CA-FV) model for macroscopic fluid flow, heat transfer, solute transport and microscopic nucleation and grain growth procedure was developed and applied in an Al-Si binary alloy solidification process. The model reflects the dendrite growth kinetics in the presence of fluid flow, the nucleation and growth in CA scale due to the increase of undercooling, and the feedback of solid fraction and temperature to FV nodes due to the nucleation and growth. The coupled CA-FV model can predict the recalescence and the intergranular segregation during alloy solidification process, which shows great advantages compared with the results by FV model and CA-FV model without fluid flow. The effects of fluid flow on the solute distribution and the solidification morphologies, as well as the influence of ingot size on the solidification structures, were discussed with the CA-FV model.
文章编号:1004-0609(2012)07-1883-14
张红伟1,NAKAJIMA Keiji 2,王恩刚1,赫冀成1
(1. 东北大学 材料电磁过程研究教育部重点实验室,沈阳 110004;
2. Division of Applied Process Metallurgy, Department of Materials Science and Engineering,
Royal Institute of Technology (KTH), Stockholm SE-10044, Sweden)
摘 要:建立凝固过程中宏观流动、传热、溶质传输与微观形核、生长过程双向耦合数学模型,并针对Al-Si二元合金凝固过程进行二维元胞自动机-控制容积积分法(CA-FV)耦合模拟。模型反映了流场下晶体逆流生长特性,考虑了温降导致的形核和生长以及形核和生长引起的固相分率变化对宏观场的影响,能预测凝固过程中再辉和晶间偏析等现象,反映合金液流动对合金的溶质分布以及凝固组织形貌的作用规律。与仅宏观传输模拟结果和无流动影响的模拟结果进行了对比,验证了耦合模型的优越性。同时考察了铸型尺寸对凝固组织形貌的影响。
关键词:Al-Si合金;凝固;晶体生长;宏观偏析;元胞自动机-控制容积积分法
中图分类号:TG27 文献标志码:A
ZHANG Hong-wei1, NAKAJIMA Keiji2, WANG En-gang1, HE Ji-cheng1
(1. Key Laboratory of Electromagnetic Processing of Materials, Ministry of Education,
Northeastern University, Shenyang 110004, China;
2. Division of Applied Process Metallurgy, Department of Materials Science and Engineering,
Royal Institute of Technology (KTH), Stockholm SE-10044, Sweden)
Abstract: A coupled cellular automaton-finite volume (CA-FV) model for macroscopic fluid flow, heat transfer, solute transport and microscopic nucleation and grain growth procedure was developed and applied in an Al-Si binary alloy solidification process. The model reflects the dendrite growth kinetics in the presence of fluid flow, the nucleation and growth in CA scale due to the increase of undercooling, and the feedback of solid fraction and temperature to FV nodes due to the nucleation and growth. The coupled CA-FV model can predict the recalescence and the intergranular segregation during alloy solidification process, which shows great advantages compared with the results by FV model and CA-FV model without fluid flow. The effects of fluid flow on the solute distribution and the solidification morphologies, as well as the influence of ingot size on the solidification structures, were discussed with the CA-FV model.
Key words: Al-Si alloy; solidification; grain growth; macrosegregation; cellular automaton-finite volume method
合金的凝固过程涉及宏观传输(传热、传质、流动)、相变热力学(相平衡、相界面、化学衡)与凝固动力学(溶质再分配、形核、生长)等多种复杂现象。鉴于宏观传热、传质和流动影响微观形核和生长的温度和浓度条件,而微观形核和生长释放的潜热又反过来影响温度和溶质等宏观场的分布,因此,有必要将宏观传输过程与微观形核生长过程相结合,通过建立合理的数学模型,获得更符合实际凝固过程的模拟结果,实现对凝固组织的预测和控制,从而获得需要的合金制品的质量及性能。
BENNON 和INCROPERA[1]建立了层流下二元合金的连续介质宏观传输模型, ABOUTALEBI等[2]将该模型应用于连铸过程中,建立了二维凝固传热、紊流流动和溶质传输模型,模拟分析了方坯和圆坯内凝固坯壳分布及宏观偏析。之后,徐建辉等[3]、陈卫德等[4]、顾江平等[5]、YANG等[6]通过采用Scheil模型,考虑凝固收缩、固相扩散及其他合金元素的影响等分别对模型进行了扩展。
形核模型分为瞬间形核模型和连续形核模型[7]。瞬间模型在某一临界过冷度下瞬间全部形核。连续形核模型(OLDFIELD[8],RAPPAZ[9])认为形核密度是过冷度的连续分布函数(如高斯分布),该模型考虑了形核过冷度的影响和形核的连续性,目前已被较广泛地应用于晶体生长的模拟中。
在晶体生长动力学研究方面,对于扩散生长条件,依据不同生长模式,共晶生长动力学常采用JACKSON和HUNT模型[10],而枝晶尖端生长动力学常采用KGT模型[11]。当存在流体流动时,GANDIN等[12]提出了流场下的枝晶尖端生长动力学模型(GGAN模型)。
对凝固组织进行预测的方法主要有Cellular automaton(CA, 元胞自动机)法、Monte Carlo(MC)法 和Phase field(PF, 相场)法。相场法属于确定模型,能够将凝固过程的溶质守恒方程与形核、生长过程耦合起来。通过在模型中引入相场函数来区分不同相区,避免了跟踪相界面的困难。相场方程反映了扩散、有序化势与热力学驱动力的综合作用,将相场方程与温度场、溶质场、流场及其他外场耦合,可对金属液的凝固过程进行真实的模拟,并能够清晰显示凝固过程中枝晶长大和粗化的生长细节。不足的是,受计算条件限制,模拟尺寸较小。CA法和MC法属于随机模型,能够将凝固过程的能量方程与形核和生长过程相结合,模拟过程中跟踪固液界面的移动,适于描述柱状晶的形成及与等轴晶间的转变。其中,MC法基于界面能最小原理,依据界面能的改变随机概率取样确定形核和生长位置,方法主要依赖凝固热力学原理,缺乏对晶粒生长动力学物理机制的考虑,其时间步长也与实际凝固时间无关。而CA模型考虑了异质形核和生长过程的物理机制。RAPPAZ 和GANDIN[13]首 先建立了介观尺度的CA模型,模型中形核位置和新晶核的结晶方向随机确定,通过引入枝晶尖端生长动力学描述晶核的长大。其计算速度快,可模拟较大尺寸铸件。ZHU和HONG[14]进一步建立了微观尺度的CA模型,考虑了固液相中的溶质扩散和溶质再分配,实现对枝晶臂生长细节的描述。
微观偏析模型是联系宏、微观过程的纽带,它描述在枝晶臂间距范围内发生的局部溶质扩散过程,通常基于微观计算域内的溶质质量平衡来进行推导。杠杆定 律和Gulliver-Scheil(GS)模型[15-16]是两种极限情况,杠杆定律体现平衡凝固,溶质在固、液两相均充分扩散;GS模型则设定溶质在液相充分扩散而在固相无扩散。实际的扩散介于这两种极限情况之间,为此,BRODY和FLEMINGS[17]、OHNAKA[18]、KOBAYASHI[19]、NI和BECKERMANN[20]及GANDIN等[21]分别针对固相反扩散给出了不同的修正模型。
将宏观流动、传热、溶质传输模型与元胞自动机组织预测模型相耦合,结合杠杆定律,GUILLEMOT等[22-23]对Pb-Sn和Ga-In合金凝固过程进行了模拟,获得的通道偏析形状和位置与实验结果吻合较好。
本文作者针对Al-Si二元合金凝固过程,建立宏观流动、传热和溶质传输与微观形核和生长过程双向耦合模型,采用杠杆定律联系热焓、浓度与温度和固相分率间的微元关系,由CA模型预测Al-Si合金枝晶生长过程。实现对凝固过程中再辉、晶间偏析和枝晶逆流生长的预测,并分析合金液流动及铸型尺寸对合金的溶质分布以及凝固组织形貌的作用规律。
1 宏观和微观耦合模型
针对Al-Si二元合金,采用控制容积法建立宏观流动、传热和溶质传输模型,采用CA模型模拟微观形核和生长过程,由杠杆定律联系微观界面热力学平衡,实现双向耦合。
1.1 宏观传输数学模型
该模型基于如下假设:1)所研究的过程为固定坐标系下的非稳态层流凝固过程;2)介质为不可压缩的牛顿流体,符合Boussinesq关于密度的假设条件;3)凝固过程中遵循局部热力学平衡,局部溶质平衡;4)所研究的体系为惰性体系,即各相孤立存在,各溶质在原子级上不可分割,各相均为连续相;5)合金固、液相具有相同的密度(ρ)和定压比热容(cp);导热系数(κ)为温度的函数,液相扩散系数(Dl)为常数;6)凝固过程以柱状晶生长方式进行,并忽略孔隙生成。
1.1.1 连续介质传输方程[24]
![]() (1)
(1)
![]()
![]() (2)
(2)
沿重力方向的体积力项为-ρg[βT(T-Tref)+ βs(wl-wref)],水平方向的体积力为0。依据Kozeny- Carman公式[25],当相密度为常量时,渗透率可表示为
![]() ,fl为液相质量分数,K0为渗透率系
,fl为液相质量分数,K0为渗透率系
数,由所研究的多相区域结构确定。则在完全凝固区(fl=0)和液相区(fl=1),渗透率分别为Kp=0和Kp=?。
![]()
![]() (3)
(3)
式中:有效导热系数为固、液相的混合值κeff=κlfl+κsfs。
![]()
![]() (4)
(4)
式中:w为溶质Si的浓度;忽略固相扩散,有效扩散系数Γeff=flρDl。
1.1.2 单元热焓和浓度与温度和固相分率的转换关系
假定相界面处保持局部溶质守恒,这并不排除相中溶质存在梯度,但忽略了溶质原子通过相界面传输的阻力。由局部的动态热平衡,忽略固液相线的曲率,可得到杠杆定律描述的单元热焓和浓度与温度和固相分率的转换关系。
设定当前时刻的热焓和浓度分别为H和w,分为以下几种情况计算出该单元的温度T和固相分率fs。
1) 单元为液相
![]() (5a)
(5a)
fs=0 (5b)
2) 单元处于两相区(fs<1)
当Hliq>H≥Heut时,有
![]() (6a)
(6a)
![]() (6b)
(6b)
当Heut>H>Hsol时,有
T=Te (7a)
![]() (7b)
(7b)
式中:Hliq=cpTliq(w)+?Hf,Hsol=cpTsol(w),Heut=cpTe+ ?Hf (1-fs, eut),fs, eut为共晶等温线上溶质浓度w对应的
固相分率。液相线温度 ![]() ,固相线温度
,固相线温度 ![]() ,Te、we和wes分别为
,Te、we和wes分别为
Al-Si合金的共晶转变温度和相应的液相和固相溶质浓度。
3) 单元为固相(Hsol≥H)
T=H/cp (8a)
fs=1 (8b)
然后,依据式(9)和(10)更新固、液相成分,液相浓度为
![]() (9)
(9)
平衡分配系数为
![]() (10)
(10)
1.2 凝固组织演化数学模型
1.2.1 形核模型
采用瞬间形核模型[26]。首先对铸型壁和熔液内部分别进行临界过冷度的预置:依据高斯分布函数,在模拟区域内随机选定CA单元位置并预置一组连续分布的临界形核过冷度。一个CA单元仅能唯一分配一个形核过冷度值。之后,在凝固过程中,当模拟区域内某CA单元的过冷度达到该点预置的临界过冷度时则形核。由二维区域上等轴枝晶的四折对称性,新生
晶核的取向为![]() 间的一随机角度,
间的一随机角度,![]() ,ranl为0~1之间的随机数。
,ranl为0~1之间的随机数。
1.2.2 流场下枝晶尖端生长动力学模型[27]
在合金凝固过程中,流体流动加快了枝晶迎流方向边界层上的质量传输,提高了成分过冷度,从而使流场下枝晶尖端生长动力学与纯扩散生长条件相比,发生了显著的改变。采用GGAN模型[12]进行描述。
将枝晶尖端过冷度?T表示为成分过冷?Tc与曲率过冷?Tr之和:
![]() (11)
(11)
超饱和度定义为
![]() (12)
(12)
流场下超饱和度与生长Peclet 数Pev间关系式(GGAN模型[12])为
![]()
![]() (13)
(13)
由界面稳定性准则,有
![]() (14)
(14)
式中:生长Peclet 数![]() ;流动Peclet 数
;流动Peclet 数![]() ;Reynolds数
;Reynolds数![]() ;Schmidt数
;Schmidt数 ![]() ,v为运动黏度;常数A=0.577 3、 B=0.659 6、C=0.524 9;指数积分函数E1(Pev)=
,v为运动黏度;常数A=0.577 3、 B=0.659 6、C=0.524 9;指数积分函数E1(Pev)=
![]() 由多项式插值进行计算[28];θ为枝晶生
由多项式插值进行计算[28];θ为枝晶生
长方向与流动方向的夹角;u为相对于固态枝晶尖端的流体流动速度,这里,假定固相枝晶静止,则u即为宏观流动计算出的局部速度;vtip为枝晶尖端生长速度;Dl为液相扩散系数;稳定性常数σ*取(4π2)-1;m为液相线斜率,Γ为Gibbs-Thomson 系数。
联立式(11)~(14),通过输入局部过冷度?T、宏观流动速度u及方向夹角θ,即可得到枝晶生长半径r和枝晶尖端生长速度vtip的值。
1.2.3 偏心生长捕获算子[22,27]
流场下合金凝固过程中,随着枝晶臂与流动方向夹角的不同,其尖端生长速度不同。这样,晶核的生长轮廓逐渐变为不规则形状。二维模拟时,晶核的生长轮廓为不规则四边形。为此,建立不规则四边形的生长捕获算子,模拟枝晶的生长演变。
取CA网格中二相邻单元点m和n。其中,点m为已形核点,其晶体生长中心设为Gm,某时刻的生长轮廓如图1中虚线所示。可以看出,从生长中心出发构成生长轮廓四边形的4条枝晶臂长度(沿á10?方向) 不等。点n在被捕获前为液态。经过一定时间步后,点m所在的晶体逐渐长大至图中细实线所示的轮廓线,此时点m晶体的生长面超过点n,点n即被点m晶体的生长所捕获,状态变为固态,其生长轮廓在继承点m生长轮廓的基础上依据截取规则截掉一部分,变为图中的粗实线。点n的生长中心确定为Gn,并通过几何关系确定从Gn出发的4条枝晶臂长度。虚拟生长中心坐标及枝晶臂长度的计算细节详见文献[27]。
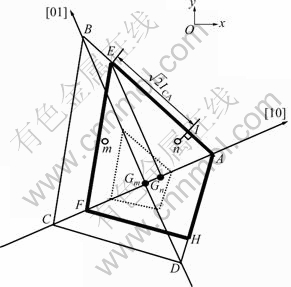
图1 二维偏心四边形生长模型[27]
Fig. 1 Two-dimensional decentred quadrilateral growth algorithm[27]
对生长轮廓进行截取的目的在于防止枝晶过度生长使得模拟结果失真。由于对生长四边形的不断截取,四边形的生长中心逐渐偏离原CA单元点,同时,由于各枝晶臂与流动方向夹角不同,导致各枝晶臂生长速度不同,即各枝晶臂长度不等,因此,二维模拟中,流场下的生长轮廓为不规则的四边形轮廓。对于每个CA单元点,需存储其对应的虚拟生长中心和各枝晶臂长度。
图2所示为一单晶粒在流场和温度场的双重作用下的生长形貌。设定一沿x轴正向流速为0.1 m/s的均匀流场,全场温度在-0.1 K/s的冷却速率下均匀冷却。晶粒的[10]取向沿x轴正向。由晶粒的生长形貌演变可以看出,流体流动破坏了枝晶生长的对称性。由于流动增强了逆流方向枝晶边界层上的质量传输,引起枝晶沿逆流方向生长速度加快。
1.3 宏观与微观的耦合过程[22]
1.3.1 宏观和微观单元变量的几何对应关系
在2D计算区域中,划分宏观FV网格与微观CA网格,其中,宏观FV网格为采用内节点法划分的较大尺寸的矩形网格,微观CA网格为枝晶臂间距数量级尺寸上的正方形网格,采用外节点法划分,与FV网格叠加在同一计算区域上。在建立宏、微观单元变量的几何对应关系时,每个宏观单元F由4个宏观节点构成,分别标识为![]() (i=1~4)。在一个宏观单元F中每个微观单元v由其中心坐标cv=(xv, yv)唯一确定。为了在宏观节点与微观CA单元之间交换信息,在每个宏观节点ni和微观CA单元v之间定义一个线性插值系数
(i=1~4)。在一个宏观单元F中每个微观单元v由其中心坐标cv=(xv, yv)唯一确定。为了在宏观节点与微观CA单元之间交换信息,在每个宏观节点ni和微观CA单元v之间定义一个线性插值系数![]() ,则可以通过以下线性插值公式由每一个宏观单元节点上的变量值
,则可以通过以下线性插值公式由每一个宏观单元节点上的变量值![]() 得到微观CA单元上的变量值ξv:
得到微观CA单元上的变量值ξv:
![]() (15)
(15)

图2 流场下的单晶生长形貌
Fig. 2 Morphology of single grain growth in presence of fluid flow
反之,当获知微观CA单元的变量值ξv时,宏观节点的变量值通过式(16)得到
![]() (16)
(16)
式中:![]() 为宏观节点n可见的微观CA单元v的个数,包括n所属各宏观单元所辖内所有CA单元;Λn
为宏观节点n可见的微观CA单元v的个数,包括n所属各宏观单元所辖内所有CA单元;Λn
为各插值系数的代数和,![]() 。
。
这里,![]() 表示在一个FV单元内各节点上变量值对内部一个CA单元v上变量值的贡献;而
表示在一个FV单元内各节点上变量值对内部一个CA单元v上变量值的贡献;而![]() /
/![]() 表示一个FV单元n上变量值得到其所见各CA单元v上变量值的贡献。
表示一个FV单元n上变量值得到其所见各CA单元v上变量值的贡献。
1.3.2 宏观和微观耦合计算
1) 微观时间步长的确定
晶粒在一个微观时间步长内生长长度不应超过一个CA单元尺寸lCA,因此,模拟枝晶演变过程需要不断调整微观时间步长,用于微观计算中的时间步长满足式(17):
![]() (17)
(17)
式中:![]() 为固液两相区中枝晶尖端生长速度的最大值;a(0<a<1)为控制微观时间步长的参数;?t为宏观时间步长。
为固液两相区中枝晶尖端生长速度的最大值;a(0<a<1)为控制微观时间步长的参数;?t为宏观时间步长。
2) 宏观单元变量插值到微观单元
通过求解宏观控制方程(1)~(4)得到FV节点上变量在一个宏观时间步?t内的变化:焓变(?Hn)、浓度变化(?wn)和速度变化(?uj, n)。
对变量进行时间线性插值,得到宏观节点n上变量在微观时间步长δt处的变化值δHn、δwn和δuj, n,再由式(15)进行空间线性插值得到微观节点v上变量的变化值δHv、δwv和δuj, v。
3) 微观单元热焓和浓度与温度和固相分率的转换
由微观CA单元上当前微观时刻的热焓、浓度值Hv和wv,采用式(5)~(8)计算出该单元的温度Tv和固相分率fs, v。
4) 更新宏观和微观节点上的变量
通过式(5)~(8)可以得出微观CA单元新的温度Tv和固相分率fs, v及其变化量δTv和δfs,v。将温度和固相分率变化量δTv和δfs,v通过式(16)再反馈给宏观节点,得到宏观节点上温度和固相分率的变化值δTn和δfs,n。
5) 宏观和微观求解过程
①宏观传输模型的离散及求解[24]
采用控制容积积分法离散宏观传输方程(1)~(4),采用SIMPLE算法处理压力和速度的耦合,上风方案离散对流-扩散方程以及能量及溶质传输方程中的对流源项,中心差分格式离散扩散源项。离散后的控制方程采用块修正及三对角矩阵法(TDMA)进行迭代求解,并对各变量进行欠松弛。为达到以下指标,在每个时间层上各方程计算3~5次:压力修正方程的源项(全场的总质量源项)小于1×10-5;能量方程的残差小于1×10-3;浓度方程的残差小于1×10-6。
②宏观和微观耦合求解
由冷却条件,通过宏观传输控制方程在FV节点上计算出热焓、浓度和速度分量,并插值到微观CA单元上。在CA单元上,由1)热焓、浓度计算出新的温度和固相分率;2)液相单元的过冷度变化计算形核,固相单元的过冷度和局部流速计算生长和捕获,从而获得CA单元状态的转变(由液相向固相)及新的温度和固相分率。将CA单元上的温度和固相分率反馈回FV节点。这样,不断冷却、形核和生长,直至全场完全凝固。宏观和微观耦合计算采用的流程图见图3。

图3 CA-FV耦合计算流程图
Fig. 3 Flow chart of CA-FV coupling algorithm
③计算结束的判据
当宏观全场固相分率fs=1时,计算结束。
④初始条件和边界条件
初始条件:全场速度初值u=v=0,初始浓度w0=0.07,初始温度T=893 K,初始液相分率fl=1。
边界条件:四壁均为固体壁面,无壁面速度。仅左壁面与外界换热,给定以焓为变量的冷却速率![]() ,其余3个壁面为绝热条件。各壁面上浓度梯度为0。
,其余3个壁面为绝热条件。各壁面上浓度梯度为0。
2 结果讨论
采用宏观和微观耦合模型,自行编制Fortran程序,针对Al-7%Si(质量分数)合金的凝固过程进行数值模拟。 Al-7%Si合金的主要物性参数和计算参数分别如表1和2所列。计算区域尺寸为30 mm×30 mm,划分宏观单元尺寸为1 mm×1 mm,微观CA单元尺寸为50 μm×50 μm,CA单元邻居采用8邻点的Moore邻居关系。
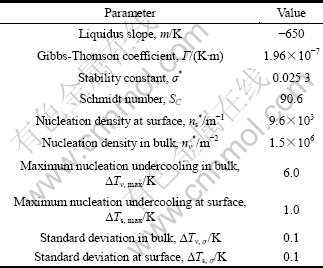
表1 宏观传输模型中Al-7%Si合金的物性参数和计算参数
Table 1 Physical properties of Al-7%Si alloy and calculation parameters in FV model

表2 微观模型中Al-7%Si合金的物性参数和计算参数
Table 2 Physical properties of Al-7%Si alloy and calculation parameters in CA model
2.1 宏观和微观耦合模拟结果
计算得到Al-7%Si合金在铸型尺寸为30 mm×30 mm,冷却速率为-4 kJ/(kg·s)的温降曲线以及温度、热焓、浓度、液相分率、凝固组织随时间演变云图和速度矢量图分别如图4~9所示。
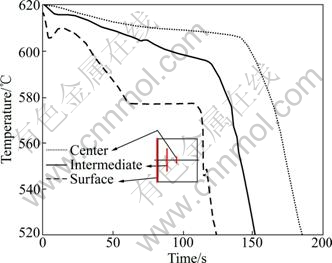
图4 Al-7%Si合金的温降曲线
Fig. 4 Evolution of temperature with time of Al-7%Si alloy
2.1.1 温降曲线
图4中3条温降曲线分别为模拟区域水平中心线上左壁面、距左壁面1/4区域处和中心处的温度随时间变化曲线。由液相线温度公式,Al-7%Si合金的液相线温度为614.05 ℃,计算初始温度取为620 ℃。由图4可见,当达到液相线温度时,合金开始凝固。凝固开始后,由于潜热释放,温降曲线变缓。当达到共晶线(577 ℃)后,保持温度不变直至完全凝固,之后,以完全固相继续降温,温降加快。从曲线上可以看到在凝固初期,由于晶体需在过冷熔体中才能形核和生长,以引起固相分率变化并释放凝固潜热,温降曲线上出现温度过冷又回复的再辉过程;凝固过程中,也多次出现温度的回复。对比3条曲线,由于设定左壁面冷却条件,在铸锭左壁面的冷却最快,中心位置最慢。
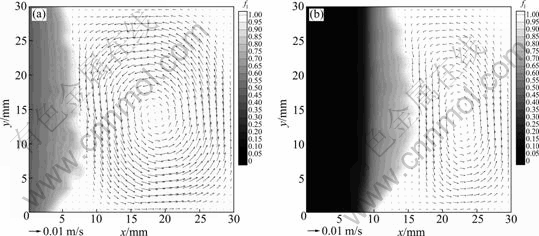
图5 Al-7%Si合金的液相分率和流场
Fig. 5 Liquid fraction and flow field of Al-7%Si alloy: (a) t=70 s; (b) t=140 s
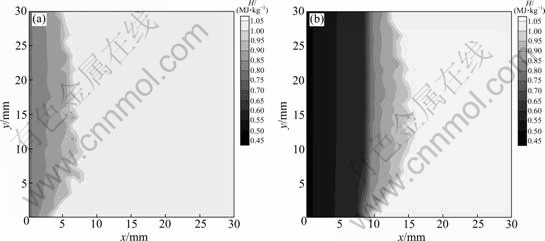
图6 Al-7%Si合金的焓场
Fig. 6 Enthalpy contours of Al-7%Si alloy: (a) t=70 s; (b) t=140 s

图7 Al-7%Si合金的温度场
Fig. 7 Temperature contours of Al-7%Si alloy: (a) t=70 s; (b) t=140 s
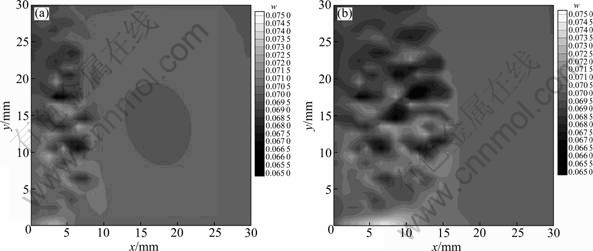
图8 Al-7%Si合金的浓度场
Fig. 8 Concentration contours of Al-7%Si alloy: (a) t=70 s; (b) t=140 s

图9 Al-7%Si合金的凝固组织
Fig. 9 Solidification morphologies of Al-7%Si alloy: (a) t=70 s; (b) t=140 s
2.1.2 流场
合金凝固过程中的流体流动受热、溶质浮力双重驱动。本计算中,温度和浓度参考点均取为初始值。而随凝固进行,温度不断下降,液相浓度不断富集,并且合金热膨胀系数为正,溶质膨胀系数为负。这样,动量方程中热浮力及溶质浮力的方向均与重力方向相同,导致凝固前沿的合金液受向下的体积力的驱动。在左壁面冷却条件下,于不断缩小的液穴内形成逆时针的回旋流动(见图5)。
2.1.3 热焓和温度场
由图6和7可知,由于仅冷却左壁面,在近左壁面区域,热焓与温度分布受热流影响较大,呈现定向凝固平界面推进的特点;而在糊状区及凝固界面前沿,受热浮力和溶质浮力双重驱动下流体流动的影响,在区域下部热焓与温度梯度较大,并且温度变化滞后于热焓变化。
2.1.4 浓度场
本研究中,合金凝固过程中的流体受热浮力和溶质浮力双重驱动,在液穴内形成逆时针回旋流动。凝固前沿液相中不断富集的溶质受流动驱动,被流体带到区域下方并向区域右端迁移,使得区域内溶质浓度在上部较低、下部较高并逐步向区域右下端末端凝固区域积聚;而在液穴芯部流动死区处溶质浓度较低。同时,在已凝固区域和糊状区内,明显可见晶内和晶间偏析(见图8)。
2.1.5 凝固组织
枝晶的迎流生长特性在这里得到很好的诠释。在左壁面冷却条件下,凝固从左壁面开始,在凝固前沿的液穴内逆时针回旋流动的流场,导致凝固前沿的枝晶生长迎向流动方向,最终形成以区域左壁面为中心的弧形固相区域。由于冷速较大,区域内以等轴晶组织为主(见图9)。
2.1.6 结果验证
YIN和KOSTER[29]对Ga-5%In(质量分数)合金进行了凝固实验,GUILLEMOT等[23]针对该实验进行了数值预测。其模拟计算选定二维区域(48 mm×33 mm),依据实验测温取定左壁面冷却速率![]() =-2.362 K/h远高于右壁面的
=-2.362 K/h远高于右壁面的![]() =-0.328 K/h),其他壁面为绝热条件。该冷却条件与本研究的相近(仅左壁面冷却、其他壁面绝热)。另外,Ga-5%In合金与Al-7%Si合金同为枝晶相凝固过程,到达共晶点凝固结束。同时,二者的溶质膨胀系数同为负值(Ga-5%In合金的溶质膨胀系数βs, In=-1.663×10-3[29],Al-7%Si合金为βs, Si= -4.0×10-2),在凝固过程中,由溶质浮力驱动流动的方向均相同,并与热浮力和重力同向。Ga-5%In合金的实验结果[29]与模拟结果[23]均表明,合金液在靠近左壁面的区域先凝固,形成以区域左壁面为中心的弧形固相区域,溶质分布亦呈现晶间偏析分布,同时,在区域下部溶质浓度较高,并逐步向末端凝固区域积聚,偏析较为严重。本模拟结果均与之相符。
=-0.328 K/h),其他壁面为绝热条件。该冷却条件与本研究的相近(仅左壁面冷却、其他壁面绝热)。另外,Ga-5%In合金与Al-7%Si合金同为枝晶相凝固过程,到达共晶点凝固结束。同时,二者的溶质膨胀系数同为负值(Ga-5%In合金的溶质膨胀系数βs, In=-1.663×10-3[29],Al-7%Si合金为βs, Si= -4.0×10-2),在凝固过程中,由溶质浮力驱动流动的方向均相同,并与热浮力和重力同向。Ga-5%In合金的实验结果[29]与模拟结果[23]均表明,合金液在靠近左壁面的区域先凝固,形成以区域左壁面为中心的弧形固相区域,溶质分布亦呈现晶间偏析分布,同时,在区域下部溶质浓度较高,并逐步向末端凝固区域积聚,偏析较为严重。本模拟结果均与之相符。
2.2 与仅模拟宏观传输结果的比较
图10所示为在相同冷却条件下,仅进行宏观传输计算(式(1)~(4)),依据杠杆定律获得温度和固相分率的更新(式(5)~(8)),而不计算微观形核和生长过程的模拟结果。对比图4可以看出,从仅宏观计算的温降曲线与宏观和微观耦合计算曲线,均可以看到潜热释放导致的温降变缓、到达共晶点后等温凝固的趋势,但仅宏观传输模型不能模拟出再辉现象,且凝固时间较短。

图10 仅宏观计算结果(铸型尺寸30 mm×30 mm, t=120 s)
Fig. 10 Macro-calculated results by finite volume model of 30 mm×30 mm ingot (t=120 s): (a) Evolution of temperature with time; (b) Concentration contour; (c) Liquid fraction and flow field
通过宏观传输计算,能够模拟出受热浮力和溶质浮力的向下驱动作用下,合金液在靠近左壁面凝固前沿的液穴内形成逆时针的回旋流动。受此影响,溶质被流体带到区域下方并向区域右端迁移,形成溶质浓度由区域上部到下部逐渐升高的梯度分布,并逐步向区域右下方凝固末端积聚。然而,仅宏观传输计算不能模拟出如图8所示的晶粒间隙或枝晶臂内的微观偏析,而这正是晶内和晶间偏聚及裂纹的成因。同时,由图10(c)液相分率分布可以看出,受强冷速的影响,凝固前沿更多呈现定向凝固平面推进的趋势。
2.3 流动对合金凝固过程的影响
采用宏观和微观耦合模型,对比有无流场条件下合金凝固过程模拟结果。不考虑流场影响的模型在初始全场静止条件下,仅耦合温度场和浓度场进行凝固模拟。
对比图4~9和图11可以看出,在不考虑流动的情况下,分别靠传导和扩散进行温度传递和溶质迁移。在本研究的左壁冷却条件下,呈现定向凝固趋势,温度和溶质分布均呈现出与凝固前沿(平行左壁面方向)平行的梯度分布。溶质在左壁处浓度最低,右壁处最高。末端凝固区域在区域的正右方。而耦合流场的计算条件下,由于受热浮力和溶质浮力作用,区域上、下部亦呈现温度和溶质浓度差异,末端凝固区域在区域的右下方。
合金液流动还显著改变了凝固组织形貌。不考虑流动模拟出的组织形貌呈定向凝固趋势,以柱状晶为主,沿热流方向生长;而考虑流动的耦合模型预测出柱状晶和等轴晶的竞争生长,并受流场影响,沿逆流方向生长较快。
2.4 铸型尺寸的影响
采用与图4~9中相同的冷却条件,研究铸型尺寸(30 mm×30 mm,10 mm×10 mm)对凝固过程的影响。
比较图4~9与图12~15可见,小铸型尺寸下,区域内流动较弱,液相分率梯度较小(见图12)。从浓度场分布(见图13)清晰可见已凝固区域存在晶间偏析和界面前沿溶质随逆时针流动向区域右下方迁移及上扬的趋势,区域底部溶质形成积聚。凝固组织呈现明显逆流生长趋势(见图14),清晰可见柱状晶向等轴晶的转变。与图9相比,柱状晶区较大。凝固末端区域在计算区域的右下方。另外,截面温差较小,凝固较快(见图15)。

图11 无流场计算结果(铸型尺寸30 mm×30 mm, 冷却速率![]() =-4 000 J/(kg·s), t=140 s)
=-4 000 J/(kg·s), t=140 s)
Fig. 11 Calculated results without fluid flow (mold size 30 mm×30 mm, cooling rate ![]() =-4 000 J/(kg·s), t=140 s): (a) Temperature contour ; (b) Concentration contour; (c) Solidification morphology
=-4 000 J/(kg·s), t=140 s): (a) Temperature contour ; (b) Concentration contour; (c) Solidification morphology

图12 Al-7%Si合金的液相分率和流场
Fig. 12 Evolution of liquid fraction and flow field of Al-7%Si alloy: (a) t=70 s; (b) t=140 s
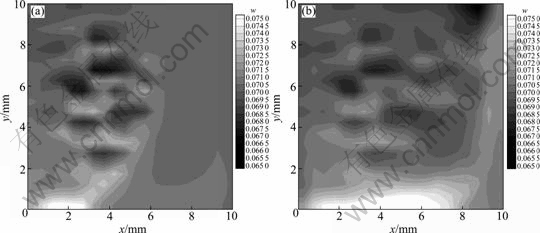
图13 Al-7%Si合金的浓度场
Fig. 13 Concentration contours of Al-7%Si alloy: (a) t=70 s; (b) t=140 s

图14 Al-7%Si合金的凝固组织形貌
Fig. 14 Solidification morphologies of Al-7%Si alloy: (a) t=70 s; (b) t=140 s
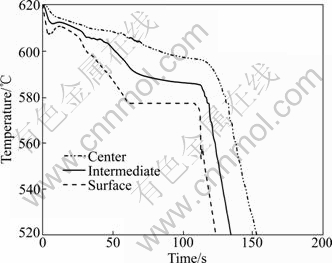
图15 Al-7%Si合金的温降曲线
Fig. 15 Evolution of temperature with time of Al-7%Si alloy
3 结论
1) 依据宏观传输理论及合金微观形核和生长理论,建立了模拟宏观流动、传热、溶质传输与微观形核、生长过程的双向耦合模型,在二维平面上采用元胞自动机模型结合控制容积积分法对Al-7%Si合金凝固过程进行了数值模拟。
2) 宏观和微观耦合模型综合考虑了流场下晶体的逆流生长、温降导致的形核和生长以及形核和生长引起的固相分率变化对宏观场的影响,能再现凝固过程中再辉和晶间偏析等现象。
3) 在左壁面冷却条件下,Al-Si合金液在热浮力和溶质浮力双重驱动下作逆时针回旋流动,在区域内形成上部溶质浓度较低、下部溶质浓度较高并逐步向凝固末端区域积聚的分布。
4) 在左壁面冷却条件下,考虑流动的耦合模型预测出柱状晶和等轴晶的竞争生长,并形成沿逆流方向生长较快的弧形固相区。
5) 在较大铸型尺寸条件下,流体有充分回旋流动空间,有利于均匀传热和传质。较小铸型尺寸溶质偏析严重,晶体迎流生长趋势明显。
REFERENCES
[1] BENNON W D, INCROPERA F P. Numerical simulation of binary solidification in a vertical channel with thermal and solutal mixed convection [J]. International Journal of Heat and Mass Transfer, 1988, 31: 2147-2160.
[2] ABOUTALEBI M R, HASAN M, GUTHRIE R I L. Coupled turbulent flow, heat, and solute transport in continuous casting processes [J]. Metallurgical and Materials Transactions, 1995, 26B: 731-744.
[3] 徐建辉, 杨秉俭,苏俊义. 考虑凝固收缩作用的凝固过程及其液相流动的有限元计算模拟[J]. 南昌航空工业学院学报, 1995, 2(2): 11-17.
XU Jian-hui, YANG Bing-jian, SU Jun-yi. On the solidification process in consideration of shrinkage and the FEM model for interdentric flow in liquid state [J]. Journal of Nanchang Institute of Aeronautical Technology, 1995, 2(2): 11-17.
[4] 陈卫德, 郑贤淑, 金俊泽. 铸锭凝固行为的数值模拟[J]. 金属学报, 1996, 32(10): 1023-1026.
CHEN Wei-de, ZHENG Xian-shu, JIN Jun-ze Numerical simulation of solidifying behaviour of cast ingot [J]. Acta Metallurgica Sinica, 1996, 32(10): 1023-1026.
[5] 顾江平, 刘 庄, 陈晓慈. 定向凝固钢锭中宏观偏析的预测. Ⅰ: 数学模型[J]. 金属学报, 1997, 33(5): 461-465.
GU Jiang-ping, LIU Zhuang, CHEN Xiao-ci. Prediction of macrosegregation of unidirectionally solidified steel ingots:.Ⅰ: Mathematical model [J]. Acta Metallurgica Sinica, 1997, 33(5): 461-465.
[6] YANG H L, ZHAO L G, ZHANG X Z, DENG K, LI W, GAN Y. Mathematical simulation on coupled flow, heat, and solute transport in slab continuous casting process [J]. Metallurgical and Materials Transactions, 1998, 29B: 1345-1356.
[7] STEFANESCU D M. Methodologies for modeling of solidification microstructure and their capabilities [J]. ISIJ International, 1995, 35(6): 637-650.
[8] OLDFIELD W. A quantitative approach to casting solidification,
freezing of cast iron [J]. Transactions of the American
Society for Metals, 1966, 59: 945-960.
[9] RAPPAZ M. Modeling of microstructure formation in solidification processes [J]. International Materials Reviews, 1989, 34(3): 93-123.
[10] JACKSON K A, HUNT J D. Lamellar and rod eutectic growth [J]. Transactions of the Metallurgical Society of AIME, 1966, 236: 1129-1142.
[11] KURZ W, GIOVANOLA B, TRIVEDI R. Theory of microstructural development during rapid solidification [J]. Acta Metallurgica, 1986, 34(5): 823-830.
[12] GANDIN C A, GUILLEMOT G, APPOLAIRE B, NIANE N T. Boundary layer correlation for dendrite tip growth with fluid flow [J]. Materials Science and Engineering A, 2003, 342: 44- 50.
[13] RAPPAZ M, GANDIN C A. Probabilistic modelling of microstructure formation in
solidification processes [J]. Acta Metallurgica et Materialia, 1993, 41(2): 345-360.
[14] ZHU M F, HONG C P. A modified cellular automaton model for the simulation of dendritic growth in solidification of alloys [J]. ISIJ International, 2001, 41(5): 436-445.
[15] GULLIVER G H. Quantitative effect of rapid cooling upon the constitution of
binary alloys [J]. Journal of the Institute of Metals, 1913, 9: 120-157.
[16] SCHEIL E. Bemerkungen zur schichtkristallbildung (Retrograde saturation
curves) [J]. Zeitschrift für Metallkunde, 1942, 34: 70-74.
[17] BRODY H D, FLEMINGS M C. Solute redistribution in dendritic solidification [J]. Transactions of the Metallurgical Society of AIME, 1966, 236: 615-623.
[18] OHNAKA I. Solute redistribution with back-diffusion in solid during solidification process [J]. Tetsu-to-Hagané, 1984, 70: S913.
[19] KOBAYASHI S. A mathematical model for solute redistribution during dendritic solidification [J]. Transactions of the Iron and Steel Institute of Japan, 1988, 28: 535-541.
[20] NI J, BECKERMANN C. A volume-averaged two- phase model for transport phenomena during solidification [J]. Metallurgical Transactions, 1991, 22B: 349-361.
[21] GANDIN C A, MOSBAH S, VOLKMANN T, HERLACH D M. Experimental and numerical modeling of equiaxed solidification in metallic alloys [J]. Acta Materialia, 2008, 56: 3023-3035.
[22] GUILLEMOT G, GANDIN C A, COMBEAU H, HERINGER R. Modeling of macrosegregation and solidification grain structures with a coupled cellular automaton—Finite element model [J]. ISIJ International, 2006, 46(6): 880-895.
[23] GUILLEMOT G, GANDIN C A, BELLET M. Interaction between single grain solidification and macrosegregation: Application of a cellular automaton—Finite element model [J]. Journal of Crystal Growth, 2007, 303: 58-68.
[24] 张红伟, 王恩刚, 赫冀成. 方坯连铸过程中钢液流动、凝固及溶质分布的耦合数值模拟[J]. 金属学报, 2002, 38(1): 99-104.
ZHANG Hong-wei, WANG En-gang, HE Ji-cheng. Coupled numerical simulation on fluid flow, solidification and solute transport in billet continuous casting process [J]. Acta Metallurgica Sinica, 2002, 38(1): 99-104.
[25] ASAI S, MUCHI I. Theoretical analysis and model experiments on the formation mechanism of channel-type segregation [J]. Transactions of the Iron and Steel Institute of Japan, 1978, 18: 90-98.
[26] GANDIN C A, DESBIOLLES J L, RAPPAZ M, THEROZ P. A three-dimensional cellular automaton—Finite element model for the prediction of solidification grain structures [J]. Metallurgical and Materials Transactions, 1999, 30A: 3153-3165.
[27] ZHANG H W, NAKAJIMA K, XING W, WANG A L, HE J C. Influences of flow intensity, cooling rate and nucleation density at ingot surface on deflective growth of dendrites for Al-based alloy [J]. ISIJ International, 2009, 49(7): 1010-1018.
[28] ABRAMOWITZ M, STEGUN I A. Handbook of mathematical functions [M]. 10th ed. New York: Dover Publications, 1972: 231.
[29] YIN H B, KOSTER J N. In situ observation of concentrational stratification and solid-liquid interface morphology during Ga-5% In alloy melt solidification [J]. Journal of Crystal Growth, 1999, 205: 590-606.
(编辑 陈卫萍)
基金项目:国家自然科学基金重点项目(50834009);高等学校学科创新引智计划资助项目(B07015);中央高校基本科研业务费资助项目(N100409004);辽宁省自然基金资助项目(20072033)
收稿日期:2011-07-08;修订日期:2011-11-18
通信作者:张红伟,副教授,博士;电话:024-83684941;E-mail: hongweizhang@epm.neu.edu.cn

