文章编号：1004-0609(2014)06-1408-06

铝裂纹扩展行为的分子动力学模拟

刘晓波，徐庆军，刘  剑

(南昌航空大学 航空制造工程学院，南昌 330063)

摘  要：采用分子动力学方法研究铝的裂纹扩展行为。建立铝的分子动力学模拟模型，通过嵌入原子法进行模拟，得到铝裂纹扩展过程中的原子轨迹图与能量演变图。从裂纹扩展图清楚地观察到裂纹扩展的变化情况：裂纹尖端钝化、子裂纹的产生、孔洞的生成及长大过程以及裂纹和孔洞的汇集。能量演变图中详细地说明了整个体系演变的过程。探讨加载速率和初始裂纹长度对体系裂纹扩展行为的影响。结果表明：随着加载速率的增大，原子运动程度加剧，体系完全被拉开的时间缩短；初始裂纹长度越长，原子运动的细节表现越不明显。

关键词：铝；裂纹扩展；分子动力学模拟；能量演变；加载速率；初始裂纹长度

中图分类号：TG146.2        　   　     文献标志码：A

Molecular dynamics simulation of crack propagation behavior of aluminum

LIU Xiao-bo, XU Qing-jun, LIU Jian

(School of Aeronautical Manufacturing Engineering, Nanchang Hangkong University, Nanchang 330063, China)

Abstract: The crack propagation behavior of aluminum was studied by molecular dynamics method. The molecular dynamics simulation model of aluminum was set up, and the energy evolution map and atomic trajectory figure of aluminum crack propagation process were obtained according to the modified embedded atom method. By plotting the crack propagation graph, the change of crack propagation is observed clearly, such as the crack tip blunted, the generation of sub-crack, the formation and growth process of the void, and the collection of crack and void. The whole evolution process of the system was described in detail from energy evolution map. The effects of loading rate and initial crack length on the crack propagation behavior of the system were discussed. The results show that the degree of atomic motion is intensified and the time of system completely open is shortened with increasing the loading rate. The longer the initial crack length is, the more unobvious the details of the atomic motion are.

Key words: aluminum; crack propagation; molecular dynamics simulation; energy evolution; loading rate; initial crack length

铝金属在制造使用过程中，不可避免地会出现微裂纹、孔洞等缺陷，而这些缺陷逐步演变，将导致材料的失效破坏，因此，必须掌握这种微观缺陷的演变规律。分子动力学模拟作为计算机模拟中非常重要的一种方法，在许多领域起着至关重要的作用，尤其在描述微观层次的细节方面。分子动力学是指对原子核和电子所构成的多体系统，求解运动方程，是一种能够解决大量原子组成的系统动力学问题的计算方法。这种方法不仅可以直接模拟许多物质的宏观演变特性，得出与实验结果相符合或相近的计算结果，而且可以提供微观结构、粒子运动以及它们和物质宏观性质关系的明确图像，从而为新的理论和概念的发展提供有力的技术支撑。

目前，国内外学者在裂纹扩展的分子动力学模拟方面做了大量的研究工作。STALEY等^[1]和MACHOVA等^[2]采用不同的势函数对裂纹萌生与扩展进行了分子动力学模拟，得到了不同因素对于裂纹萌生与扩展的影响。MAKI-JASKARI等^[3]利用经典分子动力学方法的研究表明，通过理想化的模型，在裂纹尖端或者裂纹萌生阶段形成稳定的环状结构，能够阻止裂纹的萌生，尤其是在早期的断裂阶段。周国辉等^[4]对铝单晶中心贯穿微裂纹的愈合过程进行了分子动力学模拟，结果表明，当加热温度超过临界温度或外加压应力超过临界值时，微裂纹将完全愈合。在裂纹愈合过程中伴随着位错的产生和运动以及孪晶和空位的产生及变迁。WEI等^[5]采用分子动力学模拟BCC铁材料微裂纹愈合的结果表明，温度对微裂纹愈合过程有显著影响。王晓娟等^[6]使用三维分子动力学方法模拟了单晶铝预制初始裂纹扩展过程，研究了裂纹扩展机理及温度对裂纹扩展过程的影响。WU等^[7]采用分子动力学方法研究了温度对单晶镍材料裂纹扩展的影响，结果表明，裂纹扩展过程和应力分布特征是密切相关的，温度的变化引起单晶镍裂纹生长。单德彬等^[8]对单晶铜弯曲的裂纹萌生和扩展进行了分子动力学模拟，得到了裂纹萌生和扩展的微观机理。郭雅芳等^[9]运用分子动力学模拟方法研究了原子弛豫对于裂尖场的影响，通过对体心立方铁的裂纹扩展进行研究，揭示了其裂纹扩展机理。CAO等^[10]对大块纳米镍晶 界破裂及裂纹成核进行了分子动力学模拟，结果表明，晶界脱聚是纳米镍晶的基本变形机制之一。曾祥国等^[11]对镁合金的缩孔和微裂纹进行了分子动力学模拟，揭示了镁合金塑性变形和失效机制。ZHANG等^[12]在室温下使用分子动力学模拟了单晶UO₂的断裂行为，证实了裂纹尖端的屏蔽机制、位错发射和亚温组织相的传递，探讨了裂纹尖端的变形机制。赵艳红等^[13]利用分子动力学方法，对含孔洞的金属铜进行拉伸至材料断裂模拟研究，发现在较弱负压下，孔洞及材料为弹性变形，超过一定阈值时出现塑性变形，并在局部出现相变。在极强的负压下，随拉伸应力的增加，材料经历弹性均匀拉伸、局部FCC到HCP的相变及缺陷的产生、缺陷积累产生微裂纹或空洞直至材料断裂的过程。朱志雄等^[14]采用分子动力学方法对Ni₃Al和NiAl合金在不同冷却速度下的凝固过程进行了研究，分析冷却过程中不同温度下的偶分布函数、能量和体积的变化。邱克强等^[15]采用分子动力学模拟研究了Cu₆₆Ti₃₄合金在4×10¹³ K/s冷却速度下的玻璃化转变温度和原子的扩散行为，证明了用动力学方法和用热力学方法获得的玻璃转变温度之间的差异。GUO等^[16]采用分子动力学方法模拟单晶铜(100)表面纳米加工过程，研究材料的去除机理和纳米加工过程中系统的温度分布与演化规律。陈明等^[17]通过分子动力学方法，运用EAM势函数分别研究了无孔洞和有孔洞的纳米单晶铜杆的拉伸特性。KARIMI等^[18]和TANG等^[19]采用嵌入原子方法，分别研究了单晶镍和单晶镁的裂纹增长情况，获得了裂纹尖端的临界负载和应变能的分布以及影响裂纹增长的重要因素。TERENTYEV等^[20]在不同应变速率、温度和裂纹形状的条件下研究了BCC和FCC中金属裂纹的扩展和钝化行为。结果表明，分子动力学是研究微观裂纹萌生与扩展的有效方法。

然而，大多数研究者都是在材料的预制裂纹下通过原子运动轨迹图研究裂纹扩展行为的规律。对于通过原子运动轨迹图与能量演变图相结合的方式来进行裂纹行为的研究，国内外报道很少。为此，本文作者采用EAM(Embedded-atom model)势函数对铝金属的变形裂纹扩展行为进行模拟。采用VMD软件对整个裂纹图像进行可视化，以便能清楚地观察裂纹扩展情况。

1  模型的建立

铝为面心立方金属，其结构及物理特性如表1所列。

图1所示为分子动力学模拟的初始模型。此模型显示的区域大小为40a₀×40a₀×0.25a₀，a₀为一定温度下铝的晶格常数。模型体系中共计3281个原子。在XOY平面上，上层和下层对应的区域大小为40a₀×2a₀，左上层和左下层对应的区域大小为10a₀×18a₀，右层对应的区域大小为30a₀×36a₀，在左上层与左下层原子之间设置裂纹长度为10a₀。将上层原子和下层原子的作用力设定为0，将初始温度设定为1 K，以避免原子的热激活效应。本模型采用嵌入原子法进行分子动力学模拟，X和Y方向采用非周期性边界条件，Z方向采用周期性边界条件。对整个体系充分弛豫，达到平衡状态。根据本模型的大小，将中间层原子大小为40a₀×36a₀的区域和上层原子区域的Y方向上的初始速度设定为30 m/s，X和Z方向的初始速度设定为0，下层原子则固定不动。模拟的时间步长设定为1×10^-15 s，整个体系采用微正则系综(NVE)，整个程序运行6×10⁴步，期间每1000步记录原子的坐标位置、动能、势能和总能量。

表1  铝的结构及物理特性

Table 1  Structure and physical properties of aluminum

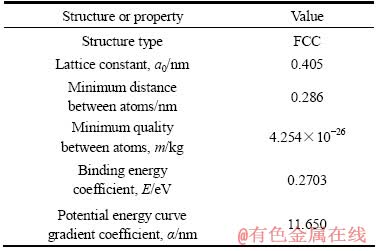
图1  分子动力学模拟的初始模型

Fig. 1  Initial model of molecular dynamics simulation

2  分子动力学模拟的势函数和算法

2.1  势函数模型

分子动力学的对象是一个粒子系统，系统中原子间的相互作用用势函数来描述，因此，正确选择势函数的类型及其参数，对于模拟的结果优劣具有重要作用。采用EAM势函数^[21]进行模拟，计算铝原子之间的相互作用，系统的总势能表示为

                     (1)

式中：F_i是原子i的嵌入能函数；是除第i个原子以外所有原子在i处产生的电子云密度之和；是第i个原子与第j个原子之间的对势作用函数；r_ij是第i个原子与第j个原子之间的距离。

2.2  模拟采用的速度算法

采用Velocity-Verlet算法，该算法给出速度、加速度和原子的位置，并且不降低精度，还给出了显式速度项，计算量适中，应用较广泛。即

             (2)

             (3)

由式(2)和(3)可推导出式(4)和(5)：

            (4)

            (5)

式中：r是原子的位置坐标；v是原子的速度；a是原子的加速度；t是原子运动时间；F是作用在原子上的力；m是相对原子质量。

该计算过程由以下步骤得到。

步骤1：给定所有原子的初始位置；

步骤2：给定初始的速度；

步骤3：给定一个极小的时间增量，通过式(2)计算在时刻原子的位置和速度；

步骤4：返回步骤2，计算下一次的原子位置。

3  结果与讨论

经过充分弛豫后，在速度加载的作用下，裂纹出现并开始扩展。对于运行结果采用可视化软件进行后处理，观察原子运动轨迹，绘制如图2所示特殊时刻体系的裂纹扩展图。

图2(a)所示为8×10³步的瞬时原子图。由图2(a)可见，裂纹已扩展至右边区域，可以看到裂纹的开口越来越大，裂纹的尖端渐渐呈现无序的现象，从这一时刻起，裂纹尖端的原子重新排列堆积，慢慢偏离理想晶格位置，因而不同于初始原子构型，在裂纹尖端出现畸变。晶体的整体性遭到破坏，模型呈现非晶状态，原子排列的混乱导致晶体的塑性变形。

图2(b)所示为体系运行到1×10⁴步时对应的瞬时原子图。从图中右边区域可以很清楚地观察到孔洞的出现。按照孔洞形核机制，一个是应力超过了原子间的结合力，原子键断裂而形成孔洞，另一个是空位的大量聚集导致孔洞。显然，这是因为塑性变形的进一步增强，个别原子之间的间隙增大，逐步发展成为空位，空位的不断发展，最终导致非常明显的孔洞出现。因此，可以推断原子的混乱排列导致孔洞的出现。随着体系的进一步运行，裂纹尖端出现更大区域的原子混乱排列，产生局部应力集中。这时裂纹要继续扩展需要克服更大的阻力。此外，裂纹尖端出现了钝化，裂纹尖端钝化后，促使裂纹张开，裂纹变得越来越宽。同时也将降低加载作用下堆积在裂纹尖端处的局部集中应力，使得裂纹尖端处的局部集中应力重新分布。

图2(c)所示为体系运行到2.5×10⁴步时的瞬时原子图。此时重新分布的局部最大应力的方向将出现新的子裂纹，从原来的裂纹平面跃迁到新的裂纹平面，从而逐渐摆脱母裂纹，形成新的裂纹尖端。并且向着集中应力小的区域扩展。

图2  不同时间步体系的裂纹扩展图

Fig. 2  Crack propagation maps of system at different time steps

图2(d)所示为体系在4.9×10⁴步时的瞬时原子图。由图2(d)可见，体系总体分为上、下两部分，可以看到微观裂纹的扩展类似于宏观裂纹，体系已经被拉开。

为了进一步说明体系裂纹的扩展情况，提取体系总能量。体系总能量演变图如图3所示。开始阶段，体系的能量不断地上升，体系不断地吸收能量，这是因为随着速度加载，原子的动能增加，体系的温度也有升高，因而加剧了原子的运动。大约在1×10⁴步时，能量有所下降，一直到2.5×10⁴步时，这一过程整个体系的能量维持在一个稳定的水平。这一阶段的特征是原子排列出现混乱，产生空位，空位不断迁移，孔洞不断吸收空位并且长大，一些原子间距离增大，接近截断半径，引起系统总势能减小，原子间的吸引力变小。从2.5×10⁴步到3.0×10⁴步，能量先升后降，出现一个小高峰值。这一阶段主要是因为裂纹要继续扩展需要克服局部应力集中，所以需要进一步吸收能量，当吸收的能量到达一定程度时，体系的能量足以克服壁垒，裂纹继续扩展，又释放大量的势能。这一阶段对应的是子裂纹的产生和子裂纹与孔洞的汇集过程。之后的能量演变过程和前一阶段的相似，随着体系的进一步运行，裂纹的开口越来越大，原子之间的势能作用越来越弱，因而导致整个体系的能量有一个逐步的微小下降过程。大约在4.9×10⁴步时，可以认为能量已经趋于平衡，这时体系已经被拉开。

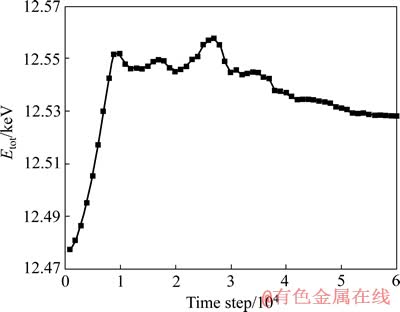
图3  体系的总能量演变图

Fig. 3  Total energy evolution diagram of system

4  影响裂纹扩展行为的主要因素

4.1  加载速率对裂纹扩展行为的影响

为了方便与初始模型所设定的加载速率v=30 m/s相比较，分别沿Y正方向施加v=20、40和60 m/s的速度加载，直到体系完全拉开，其他参数设置保持不变。图4所示为不同加载速率下体系的能量演变图。

从图4曲线a中可以看出，体系的能量也呈先增加后下降的趋势，曲线中只有一个能量高峰值，并且出现的时间要比曲线b中的晚，此后一直保持一个比较稳定的能量波动范围，因为此时的加载速率比较小，所以能量的最高值比其他速率下的能量最高值都要低。在原子运动轨迹图中并未发现明显的子裂纹与孔洞的汇集过程，这也解释了曲线a中并没有第二个能量高峰值。曲线c的形状与曲线b相似，但是曲线中的两个能量峰值都比曲线b中的大，而且出现的时间要比曲线b中的早。因为曲线c的加载速率大于曲线b的，因而其动能较高，可以看到曲线c总体能量高于曲线b的能量。另外，在原子运动轨迹图中也发现子裂纹的产生和子裂纹与孔洞的汇集时间早于曲线b中出现的时间。曲线d的形状也类似于曲线b和c，但是第二个能量高峰值出现的时间要明显早于曲线b和c出现的时间。这主要是加载速率增大，动能也随之大幅度增大，原子运动的激烈程度急剧增加，在相同的时间步数内，体系原子的位移大得多。从曲线d中也可以看出，大约从3×10⁴步后，体系的能量就达到一个非常稳定的值，结合原子运动轨迹图可知，从这之后，体系已经被拉开，拉开的时间也明显早于曲线a、b和c拉开的时间。

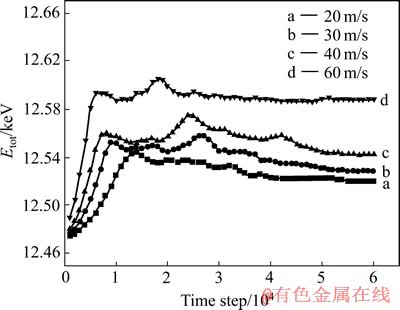
图4  不同加载速率下体系的总能量演变曲线

Fig. 4  Total energy evolution curves of system at different loading rates

4.2  初始裂纹长度对裂纹扩展行为的影响

为了与初始模型所设定的裂纹长度10a₀比较，分别设定裂纹长度6a₀和15a₀，其他条件与初始模型的条件一致，提取体系的能量。图5所示为不同设定裂纹长度下体系的能量演变图。

图5中，由于其初始加载速率保持不变，故曲线a、b和c的开始上升阶段基本沿着同一条曲线演变。曲线a能量上升到拐点的值明显大于曲线b和c的。这是因为设定的裂纹长度越短，裂纹之间的原子势能越低，导致剩下的原子势能越高，所以体系裂纹的进一步扩展需要吸收更多的能量来克服原子之间的势能。曲线c中没有出现大的孔洞聚集和长大，这是因为孔洞还来不及聚集成大的孔洞，裂纹已经与微小孔洞汇集，所以不能明显地观察到孔洞长大的过程。故曲线c的能量保持稳定的水平优于曲线a和b的。此外，曲线a对应的体系被拉开的时间步数在5.4×10⁴步左右，而曲线b的约为4.9×10⁴步，曲线c的约为4.3×10⁴步。很明显，这是因为体系X方向的长度保持不变，裂纹越长，整个体系被拉开的时间也越短。

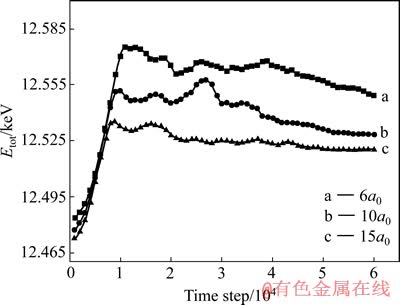
图5  不同裂纹长度下体系的总能量演变曲线

Fig. 5  Total energy evolution curves of system at different crack lengths

5  结论

1) 建立了单晶铝分子动力学模拟模型，通过特殊时刻的原子运动轨迹图和能量演变图，探讨影响裂纹扩展行为的主要因素。

2) 裂纹尖端钝化后，裂纹尖端出现无序混乱的现象，表现为裂纹尖端呈无序状态，导致裂纹尖端出现畸变。

3) 随着加载速率的增大，体系的原子运动加剧，体系完全被拉开的时间变短；初始裂纹长度越长，所需要吸收的能量越少，整个体系被拉开的时间也越 短，原子运动的细节表现越不明显。

REFERENCES

[1] STALEY J T, LIU J, HUNT W H Jr. Aluminum alloys for aerostructures[J]. Advanced Materials & Processes, 1997, 10: 17-19.

[2] MACHOVA A, KROUPA F. Atomistic modelling of contribution of dislocations to crack opening displacements[J]. Materials Science and Engineering A, 1997, 234/236: 185-188.

[3] MAKI-JASKARI M, KASKI K, KURONEN A. Simulations of crack initiation in silicon[J]. Computational Materials Science, 2000, 17: 336-342.

[4] 周国辉, 高克玮, 万发荣, 乔利杰, 褚武扬. 微裂纹愈合过程的分子动力学模拟[J]. 自然科学进展, 2001, 11(3): 300-305.

ZHOU Gou-hui, GAO Ke-wei, WAN Fa-rong, QIAO Li-jie, CHU Wu-yang. Molecular dynamics simulation of micro crack healing process[J]. Progress in Natural Science, 2001, 11(3): 300-305.

[5] WEI D B, HAN J T, TIEU K, JIANG Z Y. Simulation of crack healing in BCC Fe[J]. Scripta Materialia, 2004, 51(6): 583-587.

[6] 王晓娟, 朱宝全, 王红梅. 温度对单晶铝裂纹扩展影响的分子动力学模拟[J]. 系统仿真学报, 2010, 22(2): 534-536.

WANG Xiao-juan, ZHU Bao-quan, WANG Hong-mei. Effects of temperature on growth of monocrystalline aluminum crack: A molecular dynamics study[J]. Journal of System Simulation, 2010, 22(2): 534-536.

[7] WU Wen-ping, YAO Zong-zhuan. Molecular dynamics simulation of stress distribution and microstructure evolution ahead of a growing crack in single crystal nickel[J]. Theoretical and Applied Fracture Mechanics, 2012, 62: 67-75.

[8] 单德彬, 袁 林, 郭 斌. 单晶铜弯曲裂纹萌生和扩展的分子动力学模拟[J]. 哈尔滨工业大学学报, 2003, 35(10): 1183-1185.

SHAN De-bin, YUAN Lin, GUO Bin. Molecular dynamics simulation of bending crack initiation and growth of single crystal Cu[J]. Journal of Harbin Institute of Technology, 2003, 35(10): 1183-1185.

[9] 郭雅芳, 高索文. 分子动力学模拟裂纹扩展及相关尺寸行为[J]. 北京交通大学学报, 2005, 29(4): 5-9.

GUO Ya-fang, GAO Suo-wen. Atomistic simulation of crack propagation and its size-dependent behavior[J]. Journal of Beijing Jiaotong University, 2005, 29(4): 5-9.

[10] CAO A-jing, WEI Yue-guang. Atomistic simulations of crack nucleation and intergranular fracture in bulk nanocrystalline nickel[J]. Physical Review B, 2007, 76: 024113-5.

[11] 曾祥国, 许书生, 陈华燕. 镁合金裂纹顶端塑性变形和失效机理的分子动力学模拟[J]. 四川大学学报, 2011, 48(1): 173-178.

ZENG Xiang-guo, XU Shu-sheng, CHEN Hua-yan. Molecular dynamics simulation on plastic deformation and failure mechanisms around a crack tip for magnesium alloys[J]. Journal of Sichuan University, 2011, 48(1): 173-178.

[12] ZHANG Y F, LIU X Y, MILLETT P C, TONKS M, ANDERSSON D A, BINER B. Crack tip plasticity in single crystal UO₂: Atomistic simulations[J]. Journal of Nuclear Materials, 2012, 430(1/3): 96-105.

[13] 赵艳红, 李英骏, 杨志安, 张广财. 带孔洞的金属拉伸的分子动力学[J]. 计算物理, 2006, 23(3): 343-349.

ZHAO Yan-hong, LI Ying-jun, YANG Zhi-an, ZHANG Guang-cai. Molecular dynamics simulation of Cu with a hole under minus static pressures[J]. Chinese Journal of Computational Physics, 2006, 23(3): 343-349.

[14] 朱志雄, 张 鸿, 刘超峰, 齐卫宏, 易丹青, 李志成. Ni-Al合金凝固过程的分子动力学模拟[J]. 中国有色金属学报, 2009, 19(8): 1409-1416.

ZHU Zhi-xiong, ZHANG Hong, LIU Chao-feng, QI Wei-hong, YI Dan-qing, LI Zhi-cheng. Molecular dynamics simulation for solidification process of Ni-Al alloys[J]. The Chinese Journal of Nonferrous Metals, 2009, 19(8): 1409-1416.

[15] 邱克强, 厉 虹, 孙 晶, 尤俊华, 任英磊, 李庆丰. Cu₆₆Ti₃₄非晶合金凝固过程的分子动力学模拟[J]. 中国有色金属学报, 2011, 21(9): 2151-2156.

QIU Ke-qiang, LI Hong, SUN Jing, YOU Jun-hua, REN Ying-lei, LI Qing-feng. Solidification process of Cu₆₆Ti₃₄ amorphous alloy simulated by molecular dynamics[J]. The Chinese Journal of Nonferrous Metals, 2011, 21(9): 2151-2156.

[16] GUO Yong-bo, LIANG Ying-chun. Atomistic simulation of thermal effects and defect structures during nanomachining of copper[J]. Transactions of Nonferrous Metals Society of China, 2012, 22(11): 2762-2770.

[17] 陈 明, 李 革, 张文飞. 纳米尺度孔洞周围应力集中现象分析[J]. 材料导报B, 2011, 25(3): 131-134.

CHEN Ming, LI Ge, ZHANG Wen-fei. Discussion on the phenomenon of stress concentration around hole in nano-scale[J]. Materials Review B, 2011, 25(3): 131-134.

[18] KARIMI M, ROARTY T, KAPLAN T. Molecular dynamics simulations of crack propagation in Ni with defects[J]. Modelling Simul Mater Sci Eng, 2006, 14: 1409-1420.

[19] TANG T, KIM S H, HORSTEMEYER M F, WANG P. Atomistic modeling of crack growth in magnesium single crystal[J]. Engineering Fracture Mechanics, 2011, 78: 191-201.

[20] TERENTYEV D, ZHURKIN E E, BONNY G. Emission of full and partial dislocations from a crack in BCC and FCC metals: An atomistic study[J]. Computational Materials Science, 2012, 55: 313-321.

[21] ACKLAND G J, VITEK V. Many-body potentials and atomic-scale relaxations in noble-metal alloys[J]. Physical Review B, 1990, 41(15): 10324-10333.

(编辑  陈卫萍)

基金项目：国家自然科学基金资助项目(11362017)；江西省自然科学基金资助项目(2010GQC0803)；江西省教育厅科技落地计划科学前沿项目(KJLD12073)

收稿日期：2013-08-29；修订日期：2014-03-12

通信作者：刘晓波，教授，博士；电话：0791-83953108；E-mail: liuxb2000@sina.com