Collapse mechanism of deep tunnels with three-centered arch cross section
来源期刊:中南大学学报(英文版)2016年第12期
论文作者:李永鑫 姚聪
文章页码:3293 - 3301
Key words:deep-buried tunnel; collapse mechanism; Hoek-Brown criterion; limit analysis
Abstract: The possible collapse of different circumstances is derived with the help of the limit analysis theory. Analytical equations related to collapsing mechanisms in deep tunnel with smooth three-centered arc cross sections are derived on the basis of Hoek-Brown failure criterion and upper bound limit analysis. The pore water pressure is considered in the analysis, as a work rate of external force. Numerical results about the shape of detaching curve and the weight of collapsing block per unit length corresponding to different parameters are obtained with the help of mathematical software. The shapes of collapsing block are drawn with respected to different parameters. Furthermore, the effects of different parameters on the shape of detaching curve and the weight of the collapsing block are discussed.
J. Cent. South Univ. (2016) 23: 3293-3301
DOI: 10.1007/s11771-016-3395-3
LI Yong-xin(李永鑫), YAO Cong(姚聪)
School of Civil Engineering, Central South University, Changsha 410075, China
 Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Abstract: The possible collapse of different circumstances is derived with the help of the limit analysis theory. Analytical equations related to collapsing mechanisms in deep tunnel with smooth three-centered arc cross sections are derived on the basis of Hoek-Brown failure criterion and upper bound limit analysis. The pore water pressure is considered in the analysis, as a work rate of external force. Numerical results about the shape of detaching curve and the weight of collapsing block per unit length corresponding to different parameters are obtained with the help of mathematical software. The shapes of collapsing block are drawn with respected to different parameters. Furthermore, the effects of different parameters on the shape of detaching curve and the weight of the collapsing block are discussed.
Key words: deep-buried tunnel; collapse mechanism; Hoek-Brown criterion; limit analysis
1 Introduction
The possible collapse of a tunnel is a practical problem during the tunnel construction. It not only affects the construction schedule, but also causes the loss of lives and property. Thus, the analysis on collapse mechanisms is of obvious practical significance. Different from other structures like bridges and buildings, tunnels are constructed underground. According to the buried depths, tunnels are generally classified as shallow tunnels and deep tunnels. The effects of boundary constraints on the ground surface are always taken into consideration when analyzing collapse mechanisms of shallow tunnels. Nevertheless, deep tunnels are usually treated as the infinite solid so that boundary constraints are negligible. Despite this, the collapse mechanisms of deep tunnels are still complicated because deep-buried tunnels are located in high ground stress environment and the evolution of collapse is a complex nonlinear progress. Furthermore, the random variability of the mechanical properties of the rock in situ and the presence of cracks and fractures in rock mass are difficult to deal with as well.
The raise of the problem in practical engineering has drawn the attention of many scholars and various methods, such as the traditional stability analysis, slice method, and limit equilibrium method, have been applied to the analysis of collapse mechanisms. Due to the fact that solutions obtained from limit analysis are more rigorous and no assumption corresponding to forces is required, the limit analysis theory is widely used to the stability analysis of natural cavities and tunnels at present. LECA and DORMIEUX [1] derived the upper bound solution of the three-dimensional failure mode contained two rigid conical blocks with an internal failure surface. SUBRIN and WONG [2] proposed a new three-dimensional collapse mode which is defined by logarithmic-spirals, enveloped by a curved surface and contains a rotational movement of a single block. The results of the failure mechanism are more consistent with the experimental and numerical observations. SOUBRA [3] put forward an improved failure mode on the basis of the one established by LECA and DORMIEUX [1] and applied it to analyze the face stability of the shallow tunnel. A superior upper bound solution was derived and it was found that the improved failure mode is more consistent with the actual situation. WANG [4] constructed two new failure modes on the basis of nonlinear Mohr-Coulomb criterion and discussed about the effects of nonlinear coefficient and other rock parameters on surrounding rock pressure. FRALDI and GUARRACINO [5-7] constructed a curved failure mechanism to describe the collapse block of cavity and by virtue of the calculus of varational, the analytical solution of detaching profile corresponding to different cross sections in the realm of plasticity theory was derived. YANG et al [8-12] proposed the nonlinear theorem of limit analysis and mode thorough research on collapse mechanisms of tunnels and stability of surrounding rock on the basis of Hoek-Brown failure criterion.
Due to the fact that deep-buried tunnels are usually under water table, the influence of pore pressure can not be ignored. MICHALOWSKI [13] regarded the water pressure in the soil pores as an external force loaded on the soil skeleton. Thus, the work of water pressure in the frame of limit analysis theory can be obtained by adding the pore pressure work on skeleton to the work of the water pressure on the boundary. Based on this assumption, KIM et al [14] and VIRATJANDR and MICHALOWSKI [15] conducted limit analysis of slope stability. The collapse mechanism of circular tunnel was applied to the assumption to analyze in the frame work of limit analysis [16-18], and the numerical solution was obtained for the shape of collapsing block.
Though the approaches presented above derived collapse mechanisms of various conditions, the cross section is either simplified like a rectangular or abstracted as a curve equation. In actual engineering, the choice of tunnel cross section tends to accommodate the performance requirements of the tunnel and tries to minimize stresses in the lining. Based on a number of engineering experiences, a smooth three-centered arc cross section which is illustrated in Code for Design of Road Tunnel [19] is recommended. So, the study on collapse mechanisms of tunnels with a smooth three-centered arch cross section has large practical value in the construction of tunnels. To analyze collapse mechanisms in deep tunnels with a smooth three-centered arch cross section, this work constructs a curved failure mechanism and the rate of energy dissipation and the external rate of work are calculated within the frame work of upper bound theorem. Subsequently, with the help of variational approach, analytical expressions of the failure mechanisms are derived. Then, by substituting the equations of the cross section, the final analytical solutions of collapse mechanisms are obtained. The further study on the effects of different parameters on the shape of the detaching curve and the weight of collapsing block per unit length is conducted and the conclusion may be valuable for reference in actual engineering.
2 Tunnel cross sections in practical engineering
According to Refs. [20-25], the main features of the uniform standard of inner sections in actual engineering are smooth three-centered arc cross sections of which the arc crown and inverted arc are arcs of different radii and they are connected with an arc of a small radius. The structure of the inner sections is the same although they are divided as various types according to different traffic demands. The inner sections of standard two-lane and two-lane with emergency parking place are illustrated in Fig. 1.
The dotted line in Fig. 1 denotes the structural approach limit of tunnel which ensures the normal operation and safety of transportation in the tunnel. The parameters related to the cross section can be determined once the structural approach limit of tunnel is confirmed according to the traffic demand of the designing road.
3 Upper bound theorem with nonlinear criterion
3.1 Upper bound theorem of limit analysis
Upper bound theorem of classic plasticity theory is useful to solve the stability problems in soil mechanics.
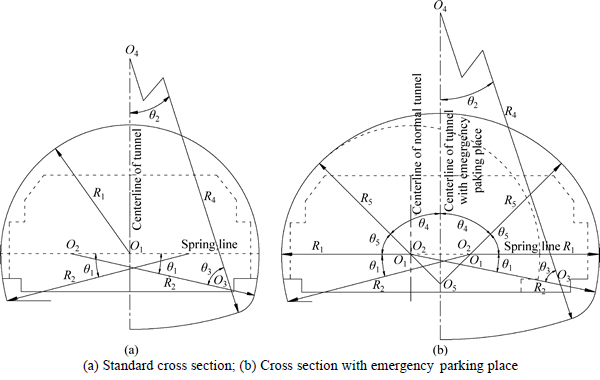
Fig. 1 Feature of three-centered arc cross sections in actual engineering:
The state of the upper bound theorem can be represented the fact that: when the velocity boundary condition is satisfied, the load derived by equating the external rate of work to the rate of the energy dissipation in any kinematically admissible velocity field is no less than the actual collapse load. Due to the fact that the deep-buried tunnels are usually under the water table, the effects of pore pressure should be taken into consideration. According to Refs. [26-29], the effects of pore pressure in the realm of the upper bound theorem are assumed that the work of water pressure is equal to the sum of the pore pressure work on skeleton expansion and the work of the water pressure on boundary. Thus, the expression of the upper bound theorem which considers the effect of pore pressure is
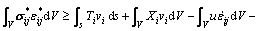
 (1)
(1)
where 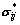 and
and  are the stress tensor and strain rate in the kinematical velocity field, respectively; Ti is a surcharge load on the boundary s; Xi is the body force; V is the volume of the mechanism; vi is the velocity along the velocity discontinuity surface; ni is the unit vector and u is the pore pressure. The upper bound theorem requires some assumptions as follows: 1) the material is perfectly plastic with convex yield function in stress space; 2) the material obeys an associated flow rule. Due to the assumptions, the strain rate
are the stress tensor and strain rate in the kinematical velocity field, respectively; Ti is a surcharge load on the boundary s; Xi is the body force; V is the volume of the mechanism; vi is the velocity along the velocity discontinuity surface; ni is the unit vector and u is the pore pressure. The upper bound theorem requires some assumptions as follows: 1) the material is perfectly plastic with convex yield function in stress space; 2) the material obeys an associated flow rule. Due to the assumptions, the strain rate  in the blocks is equal to zero, thus, only the last term on the right hand side of Eq. (1) contributes to the effects of pore pressure.
in the blocks is equal to zero, thus, only the last term on the right hand side of Eq. (1) contributes to the effects of pore pressure.
3.2 Hoek-Brown failure criterion
Because the collapse of deep tunnels is a complex nonlinear evolution process, the choice of Hoek-Brown failure criterion is better to simulate the truth. Hoek-Brown failure criterion was originally developed in order to provide input information for the design of underground excavations. Nowadays, it is widespread for tightly interlocked hard rock mass. For the convenience of research, the Hoek-Brown nonlinear failure criterion is represented in terms of normal and shear stresses as follows:
 (2)
(2)
where σn is the normal stress; τ is the shear stress; A and B are material constants; σci is the uniaxial compressive strength; σtm is the tensile strength of the rocks.
4 Limit analysis of collapsing mechanisms
4.1 Analytical solutions of arbitrary cross section
The analytical solutions for limit analysis of collapsing mechanisms in tunnels with arbitrary cross sections have been derived in Ref. [6] and further study with respect to pore pressure has been done in Ref. [16]. The main process is represented as follows for the convenience of further study.
According to Eq. (2), the energy dissipation rate determined by the internal forces is derived as
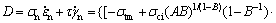
 (3)
(3)
where  and
and 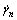 are normal and shear plastic strain rates, respectively; f ′(x) is the first derivation of f(x); w is the thickness of the detaching curve. Considering the symmetry of the detaching curve, the work rate of collapsing block produced by weight results is
are normal and shear plastic strain rates, respectively; f ′(x) is the first derivation of f(x); w is the thickness of the detaching curve. Considering the symmetry of the detaching curve, the work rate of collapsing block produced by weight results is
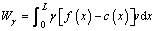 (4)
(4)
where γ is the dry unit weight of the rock mass; L is the half width of the collapsing block; and c(x) is the equation describing the profile of the tunnel. According to Ref. [13], pore pressure can be represented as
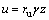 (5)
(5)
where ru is the pore pressure coefficient; z is the vertical distance between the roof of the tunnel and the top of the collapsing block. Thus, the pore pressure inducing work rate along the detaching surface can be derived by virtue of Eq. (1) and Eq. (5)
 (6)
(6)
Furthermore, the difference of the total energy dissipation rate and the total work rate done by external forces results is
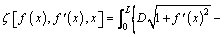
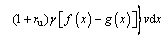
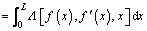 (7)
(7)
where  is a functional which can be expressed as
is a functional which can be expressed as
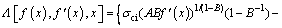
 (8)
(8)
According to the upper bound theorem and variational calculation, the problem is transformed into searching for the boundary value of the corresponding differential equation. Thus, by virtue of the definite integral calculation, the functional Λ becomes
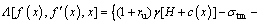
 (9)
(9)
where H is a integration constant to be determined. Thus, the expression of ζ can be derived by integrating Λ along the interval [0, L].
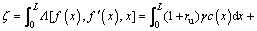
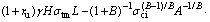
 (10)
(10)
Due to the fact that the detaching curve is symmetrical with respect to y axis, the point (0, L) should be on the detaching curve. Thus, an equation about L and H is obtained
 (11)
(11)
According to the upper bound theorem, the effective shape of collapsing block in a limit state can be determined by minimizing the difference of the total energy dissipation rate and the rate of external work. Therefore, another equation concerning about L and H is obtained by equating Eq. (10) to zero. As a result, the equation with respect to parameter L is derived
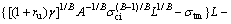
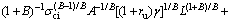
 (12)
(12)
where p is the specific generalized pressure which is defined as
 (13)
(13)
The specific generalized pressure is relevant to the detaching curve. Once the equation of the detaching curve is determined, it can be calculated. The specific equation of the detaching curve will be discussed.
4.2 Further study on smooth three-centered arc cross section
Due to the fact that the collapsing block only relates to the upper part of the inner section, the equation, c(x), which describes the tunnel profile is just about the upper cross section. It is noted from Fig. 1(a) that the upper part of the standard two-lane cross section is a semicircle of radius R1. Thus, the expression of detaching curve is a part of a circle. Consequently, collapse mechanisms of this circumstance are consistent with those of circular tunnels which have been studied. So, the relevant conclusion can make reference to Ref. [16].
As for the two-lane cross section with emergency parking place illustrated in Fig. 1(b), the upper part of the cross section consists of two kinds of different arcs. Therefore, collapse mechanisms of this condition are different. It must be pointed out that the discussion below takes example of the two-lane cross section with emergency parking place, while the circumstances of standard three-lane cross section, three-lane cross section with emergency parking place and so on can reach conclusion in the same way.
It is noted from Fig. 1(b) that the radius of arc crown is larger than that of hance. According to tunnel mechanics, the bigger the width of a tunnel is, the more possible the collapse will happen. Thus, the part of arc crown is more possible to collapse under the same circumstance.
The general ideal of analyzing the collapse mechanisms of the cross section with emergency parking place is as follows. Firstly, consider the worst condition which assumes the upper cross section to be a semicircle of radius R1. Consequently, the equation of c(x) in the Cartesian reference frame oxy illustrated in Fig. 2(a) can be expressed as
 (14)
(14)
Then, the specific generalized pressure is derived
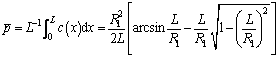 (15)
(15)
By substituting Eq. (15) into Eq. (12), a nonlinear equation with respect to L is obtained:
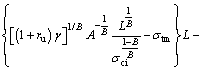
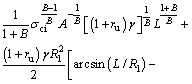
 (16)
(16)
Though the analytical solution of Eq. (16) is difficult to find, the numerical solution can be derived easily with the help of mathematical software. After that, comparing L to the half length of arc crown L0, if L≤L0, the assumption of the upper section being a semicircle of R1 is tenable and the range of collapsing block is only in the arc crown. Therefore, the numerical solution of L is the right and the other parameters can be obtained according to the equations above. Moreover, the weight of the collapsing block per unit length, P, can be derived by
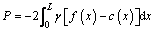
 (17)
(17)
where  is the specific generalized pressure obtained by Eq. (16).
is the specific generalized pressure obtained by Eq. (16).
Otherwise, the assumption is not valid and the range of collapsing block involves both arc crown and hance. For this circumstance, the equation of c(x) in the Cartesian reference frame oxy illustrated in Fig. 2(b) should be expressed by a piecewise function as
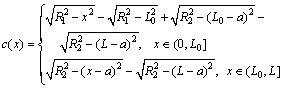 (18)
(18)
where a denotes the horizontal projective length of O1O2 and it can be calculated by the following equation:
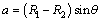 (19)
(19)
in which θ is half of the central angle of arc crown as shown in Fig. 2(b).
Thus, the specific generalized pressure can be obtained:
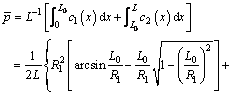
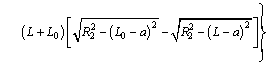 (20)
(20)
Then, combining Eq. (12) and Eq. (19), another nonlinear equation is derived as
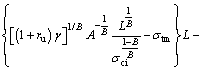
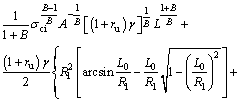
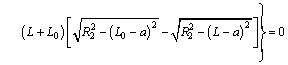 (21)
(21)
By virtue of mathematical software, the numerical solution L of Eq. (21) can be obtained and the other features of the collapsing block including the specific expression of the detaching curve and the height of the collapsing block can be obtained according to the value of L. Especially, the overall weight of the collapsing block per unit length can be calculated according to Eq. (17) while the specific generalized pressure becomes Eq. (20).
5 Numerical results and discussion
According to the above derivation, the damage form of deep tunnel with three-centered arch cross section is affected by many factors, such as pore pressure coefficient ru, unit weight γ, material constants A and B, uniaxial compressive strength σci, tensile strength σt, arch radius R1 and waist arch radius R2. In order to have an intuitive understanding of the effects of different parameters, a two-lane cross section with emergency parking place used in practical engineering is adopted for the numerical calculation and the detailed parameters is illustrated in Fig. 3.
5.1 Effects of parameters on shape of collapsing block
For the purpose of investigating effects of different parameters on the shape of the collapsing block and the convenience of comparing the results with other scholars, the rock mass parameter A ranges from 0.2 to 0.8;parameter B varies from 3/4 to 1; the tensile strength of the rock mass changes from σc/200 to σc/50; the dry unit weight varies from 15 kN/m2 to 30 kN/m2; and the pore pressure coefficient ranges from 0 to 0.75. According to the analytical equations derived above, the corresponding results are obtained with the help of mathematical software as shown in Fig. 4.
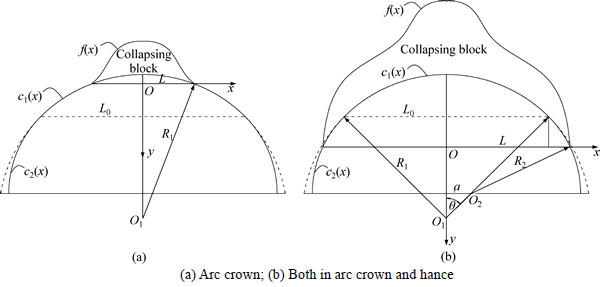
Fig. 2 Different dimensions of collapsing block:
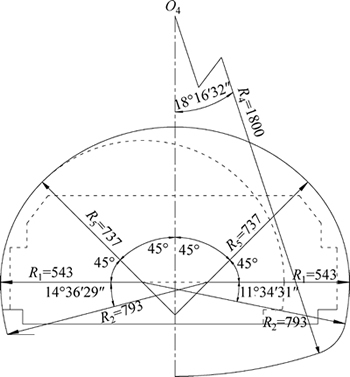
Fig. 3 Detailed parameters of a three-centered arc cross section used in practical engineering
It can be immediately found from Fig. 4 that the parameters including A, B, σt, γ and ru all affect the collapsing block to some degree. The width of the collapsing block increases with the increasing of A, σt and ru while it decreases when the value of B or γ increases. The height of the collapsing block decreases when A or γ increases but it increases with the increasing of B, σt and ru. As for the straight line of B=1 in Fig. 4(b), it can be regarded as the nonlinear that Hoek-Brown failure criterion is coincident with the linear Mohr- Coulomb failure criterion when the value of B equals 1.
Furthermore, to investigate the effects of the radii of cross section on the collapsing mechanisms, the detaching curves corresponding to A=2/3, B=3/4, σc=2.5 MPa, σt/100, γ=25 kN·m2, ru=0.5 with R1 varying from 6 m to 12 m and R2 ranging from 4.2 m to 8.4 m are obtained and illustrated in Fig. 5. Due to the fact that the range of the collapsing block only relates to the arc crown in this example, it can be regarded that the increasing of the collapsing block is due to the value of R1 increasing.

Fig. 4 Effects of different parameters on shape of collapsing block in deep tunnels with smooth three-centered arc cross sections:
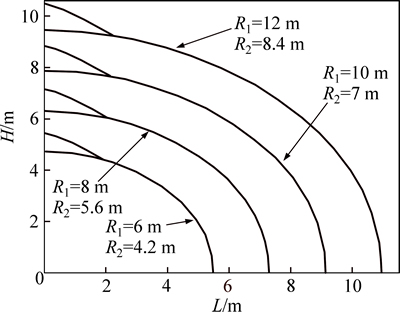
Fig. 5 Effects of radii on shape of collapsing block
5.2 Effects of parameters on collapsing magnitude
The investigation how parameters affect the shape of the collapsing block helps us to understand the collapse mechanisms of deep-buried tunnel. Studying the collapsing magnitude is of high engineering significance to the design and construction of the tunnel in the view of actual engineering because the proper reinforcement measures can be chosen when the collapsing magnitude is determined.
According to Eq. (17), the overall weight of the collapsing block per unit length with respect to different parameters can be derived with the help of mathematical software. To provide reference for practical engineering, the numerical results of P are plotted as the function of parameter A with respect to different B, σtm, γ and ru as follows.
It can be concluded from Fig. 6 that the weight of the collapsing block per unit length increases with the increasing of strength parameter A, tensile strength, dry unit weight of the rock mass and radii related to the cross section while it decreases with the increasing of strength parameter B and pore pressure coefficient. Moreover, when the values of strength parameter B and pore pressure coefficient increase, the slope of the function plotted decreases, which means the weight of the collapsing block per unit length increases at a lower speed when B and ru increase. The opposite conclusion can be obtained when the tensile strength increase. However, the slope of function seems to have no evidence change when γ and radii increases. Consequently, the drawn conclusion is that the weight of the collapsing block per unit length is sensitive to B, σtm, ru while insensitive to γ and R.

Fig. 6 Effects of different parameters on collapsing magnitude in deep tunnels with smooth three-centered arc cross sections:
6 Conclusions
1) On the basis of Hoek-Brown failure criterion and by regarding the effect of water pressure as a work rate of external force, the analytical equations of collapsing mechanisms in deep buried tunnel with smooth three-centered arc cross section which is widely used in practical engineering are derived.
2) According to the analytical equations of detaching curve, the numerical results are obtained by virtue of mathematical software and the shapes of collapsing block with respected to different parameters, including A, B, σt, γ and ru, are drawn. It is concluded that the width of the collapsing block increases with the increasing of A, σt and ru while it decreases when the value of B or γ increases. The height of the collapsing block decreases when A or γ increases but it increases with the increasing of B, σt and ru. Moreover, the effects of cross section’s radii are discussed and the conclusion that collapsing block increases with the increasing of radii is obtained.
3) By virtue of the analytical equations of overall weight of the collapsing block per unit length, the numerical solutions of P corresponding to different parameters are derived and plotted as the function of the parameter A for different B, σtm, γ, ru and radii related to the cross section for the purpose of sensitive analysis. It is found that the weight of the collapsing block per unit length increases with the increasing of strength parameter A, tensile strength, dry unit weight of the rock mass and radii related to the cross section while it decreases with the increasing of strength parameter B and pore pressure coefficient. Furthermore, the weight of the collapsing block per unit length is found sensitive to B, σtm and ru.
References
[1] LECA E, DORMIEUX L. Upper and lower bound solutions for the face stability of shallow circular tunnels in frictional materials [J]. Canada Geotechnical Journal, 1990, 40(4): 581-606.
[2] SUBRIN D, WONG H. Tunnel face stability in frictional material: A new 3D failure mechanism [J]. Comptes Rendus Mécanique, 2002, 330(7): 513-519.
[3] SOUBRA A H. Three-dimensional face stability analysis of shallow circular tunnels [C]// ISRM International Symposium. Melbourne, Australia: International Society for Rock Mechanics, 2000: 19-24.
[4] WANG Zuo-wei. Upper bound limit analysis of surrounding rock pressure in shallow tunnels subjected to nonlinear failure criteion [D]. Changsha: Central South University, 2010. (in Chinese)
[5] FRALDI M, GUARRACINO F. Limit analysis of collapse mechanisms in cavities and tunnels according to the Hoek-Brown failure criterion [J]. International Journal of Rock Mechanics and Mining Sciences, 2009, 46(4): 665-673.
[6] FRALDI M, GUARRACINO F. Analytical solutions for collapse mechanisms in tunnels with arbitrary cross sections [J]. International Journal of Solids and Structures, 2010, 47(2): 216-223.
[7] FRALDI M, GUARRACINO F. Evaluation of impending collapse in circular tunnels by analytical and numerical approaches [J]. Tunnelling and Underground Space Technology, 2011, 26(4): 507- 516.
[8] YANG X L, PAN Q J. Three-dimensional seismic and static stability of rock slopes [J]. Geomechanics and Engineering, 2015, 8(1): 97-111.
[9] YANG X L, HUANG F. Three-dimensional failure mechanism of a rectangular cavity in a Hoek–Brown rock medium [J]. International Journal of Rock Mechanics and Mining Sciences, 2013, 61: 189-195.
[10] YANG X L, HUANG F. Collapse mechanism of shallow tunnel based on nonlinear Hoek-Brown failure criterion [J]. Tunnelling and Underground Space Technology, 2011, 26(6): 686-691.
[11] YANG X L. Seismic passive pressures of earth structures by nonlinear optimization [J]. Archive of Applied Mechanics, 2011, 81(9): 1195-1202.
[12] YANG X L, WANG J M. Ground movement prediction for tunnels using simplified procedure [J]. Tunnelling and Underground Space Technology, 2011, 26(3): 462-471.
[13] MICHALOWSKI R L. Slope stability analysis: a kinematical approach [J]. Canada Geotechnique Journal, 1995, 45(2): 283-293.
[14] KIM J, SALGADO R, YU H S. Limit analysis of soil slopes subjected to pore-water pressure [J]. Journal of Geotechnical and Geoenvironmental Engineering, 1997, 125(1): 49-58.
[15] VIRATJANDR C, MICHALOWSKI R L. Limit analysis of submerged slopes subjected to water drawdown [J]. Canada Geotechnique Journal, 2006, 43(8): 802-814.
[16] YANG X L, YAN R M. Collapse mechanism for deep tunnel subjected to seepage force in layered soils [J]. Geomechanics and Engineering, 2015, 8(5): 741-756.
[17] YANG X L, QIN C B. Limit analysis of rectangular cavity subjected to seepage forces based on Hoek-Brown failure criterion [J]. Geomechanics and Engineering, 2014, 6(5): 503-515.
[18] YANG X L, ZOU J F. Cavity expansion analysis with non-linear failure criterion [J]. Proceedings of the Institution of Civil Engineers-Geotechnical Engineering, 2011, 164(1): 41-49.
[19] JTG D70-2004 Code for design of road tunnel [S].
[20] PAUL M, Hoek E. Estimating the geotechnical properties of heterogeneous rock masses such as flash [J]. Bulletin of Engineering Geology and the Environment, 2001, 60(2): 85-92.
[21] YANG X L, YIN J H. Slope equivalent Mohr-Coulomb strength parameters for rock masses satisfying the Hoek-Brown criterion [J]. Rock Mechanics and Rock Engineering, 2010, 43(4): 505-511.
[22] YANG X L. Seismic bearing capacity of a strip footing on rock slopes [J]. Canadian Geotechnical Journal, 2009, 46(8): 943-954.
[23] YANG X L, YIN J H. Slope stability analysis with nonlinear failure criterion [J]. Journal of Engineering Mechanics, 2004, 130(3): 267-273.
[24] SAADA Z, MAGHOUS S, GARNIER D. Pseudo-static analysis of tunnel face stability using the generalized Hoek-Brown strength criterion [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2013, 37(18): 3194-3212.
[25] YANG X L, DU D C. Upper bound analysis for bearing capacity of nonhomogeneous and anisotropic clay foundation [J]. KSCE Journal of Civil Engineering, 2016, 20(7): 2702-2710.
[26] YANG Xiao-li, LONG Ze-xiang. Roof collapse of shallow tunnels with limit analysis method [J]. Journal of Central South University, 2015, 22(5): 1929-1936.
[27] YANG Xiao-li, QIN Chang-bing. Limit analysis of supporting pressure in tunnels with regard to surface settlement [J]. Journal of Central South University, 2015, 22(1): 303-309.
[28] MOLLON G, DIAS D, SOUBRA A H. Probabilistic analyses of tunneling-induced ground movements [J]. Acta Geotechnica, 2013, 8(2): 181-199.
[29] MOLLON G, DIAS D, SOUBRA A H. Range of the safe retaining pressures of a pressurized tunnel face by a probabilistic approach [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2013, 139(11): 1954-1967.
(Edited by YANG Hua)
Foundation item: Project(2013CB036004) supported by Basic Research Program of China; Projects(51378510, 41302226) supported by National Natural Science Foundation of China; Project(2016zzts062) supported by Doctorial Innovation Foundation of Central South University, China
Received date: 2015-05-26; Accepted date: 2015-07-29
Corresponding author: LI Yong-xin, PhD; Tel: +86-18175151698; E-mail: 144801057@csu.edu.cn

