
Numerical simulation of solidification process of Sn-3.5%Pb hollow billet with stirring magnetic field
ZHANG Qi(张 琦), WANG Tong-min(王同敏), LI Ting-ju(李廷举), JIN Jun-ze(金俊泽)
State Key Laboratory of Materials Modification by Laser, Ion and Electron Beams,
School of Materials Science and Engineering, Dalian University of Technology, Dalian 116023, China
Received 20 December 2006; accepted 9 April 2007
Abstract: In order to study the effect of the stirring flow on the grain diameter and solute concentration of hollow billet, the couple model of the two-phase solidification and electromagnetic field was built to simulate the solidification process of Sn-3.5%Pb hollow billet with the traveling magnetic field and rotating magnetic field. The effects of different kinds of flows on the temperature field, concentration field and grain diameter of molten metal during solidification were analysed. The results show that, there are different flow patterns in the molten metal induced by the traveling magnetic field and rotating magnetic field. Both flows can refine the grains in the hollow billet because of change of the temperature gradient and cooling rate of molten metal. The bigger the stirring velocity is, the smaller the grain diameter. Both flows can result in the macro-segregation in the hollow billet because of the non-homogeneous flows. The bigger the stirring velocity, the more serious the macro-segregation of the hollow billet. So, the stirring intensity should be controlled to acquire the high quality hollow billet.
Key words: Sn-3.5%Pb alloy; traveling magnetic field; rotating magnetic field; hollow billet; temperature field; concentration field
1 Introduction
In recent years, the continuous casting hollow billets are widely used in industry, and the requirement of quality for the hollow billets is more and more rigorous. WANG et al[1] and LI et al[2] applied the electromagnetic field to improve the as-cast microstructure of continuous casting hollow billets. In order to produce big diameter hollow billet with high quality, ZHANG et al[3] put forward the technology of placing the rotating magnetic field(RMF) and the traveling magnetic field(TMF) in the inner-mold of hollow billet, and the static simulation experiments with Sn-3.5%Pb were done. The experimental results showed that there are different flow patterns in the molten metal induced by TMF and RMF. Both flows can refine the grain and improve the microstructure of hollow billet. Many scholars[4-6] studied the microstructure refining mechanism with electromagnetic field, WILLERS et al[7-8] did many experiments and found that the flow of molten metal caused by the electromagnetic field can change the cooling curve, and the temperature distribution of molten metal during solidification is the main reason for the refinement and spheroidization of microstructure. But the numerical simulation about the effect of electromagnetic field on the solidification and microstructure of molten metal was few reported. So, in order to save the experimental expenses, the couple model of the equiaxed globular grain under two-phase solidification and the electromagnetic field was established to simulate the solidification process of Sn-3.5%Pb hollow billet with TMF and RMF. The effects of the two kinds of flow on the temperature field, concentration field and grain diameter were studied, which is very useful for the choice of electromagnetic field intensity.
2 Theoretical analysis
2.1 Electromagnetic field model
The vector potential A and scalar potential  are used to solute the electromagnetic field. The following equations are established[9-10]:
are used to solute the electromagnetic field. The following equations are established[9-10]:
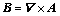 (1)
(1)
 (2)
(2)
According to Maxwell equation, the following magnetic field partial differential and electric field partial differential are acquired as:
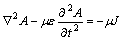 (3)
(3)
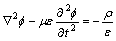 (4)
(4)
where B is magnetic induction intensity; E is magnetic field intensity; μ is permeability; ε is dielectric constant.
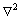 is Laplace operator,
is Laplace operator,  .
.
The finite element method is used to compute Eqns.(3) and (4) to acquire the magnetic vector potential A and electric scalar potential 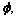 then the magnetic induction intensity, electromagnetic force and Joule heat density can be acquired as:
then the magnetic induction intensity, electromagnetic force and Joule heat density can be acquired as:
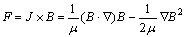 (5)
(5)
 (6)
(6)
where F is electromagnetic force density, N/m3; Q is Joule heat density, J/m3; ρ is electrical resistivity, Ω?m; t is time, s.
2.2 Two-phase solidification model
Based on the average method of volume element and the Eulerian-Eulerian method, the mass, momentum, energy and concentration conservation equations of two- phase are established[11-13].
Mass conservation equation:
 (7)
(7)
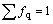 (8)
(8)
Momentum conservation equation:
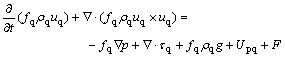 (9)
(9)
Energy conservation equation:
 (10)
(10)
Concentration conservation equation:
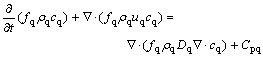 (11)
(11)
Grain transfer equation:
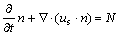 (12)
(12)
In this model, the phase transfer model that includes the nucleate and growth of the grains and the meaning of the symbols in the equations are described in Ref.[13]. It should be emphasized that the electromagnetic force density F and Joule heat density Q in Eqns.(9) and (10) are acquired from the above electromagnetic field computation.
2.3 Boundary conditions and computational para- meters
In this study, the Sn-3.5%Pb hollow billet with the dimension d 170 mm×30 mm is simulated. Fig.1 and Fig.2 show the computational model and finite element model of electromagnetic field, respectively. The parallel magnetic flux boundary is set for the computation of electromagnetic field. To solve the two-phase solidification model, the boundary condition of heat transfer with air is set on the top of molten metal, and the boundary condition of heat conduction is set on the interface of mould and molten metal. The initial temperature of molten metal is 520 K (the superheat is 30 K), and the initial solute concentration is 3.5% (mass fraction) for Sn-3.5%Pb alloy. Table 1 lists the main computation parameters.
Table 1 Main computation parameters
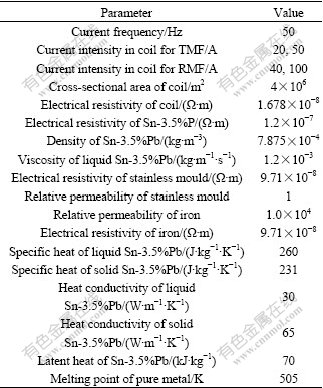
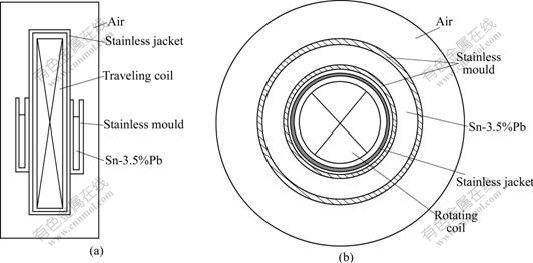
Fig.1 Computational model of electromagnetic field: (a) With traveling magnetic field; (b) With rotating magnetic field
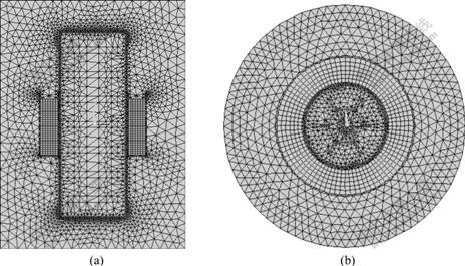
Fig.2 Finite element model of electromagnetic field: (a) With traveling magnetic field; (b) With rotating magnetic field
The following assumptions are made for computation:
1) The density, coefficient of heat conductivity and specific heat are constant;
2) The molten metal is incompressible Newtonian fluid;
3) The effect of flow of molten metal on the electromagnetic field can be neglected;
4) The effect of buoyancy force can be neglected;
5) The flow of molten metal is turbulent one.
2.4 Solution procedure
The software ANSYS? is used to compute the electromagnetic field model to acquire the electro- magnetic force density and Joule heat density[14]. Then the electromagnetic force density F and Joule heat density Q are substituted in the momentum conservation equation and energy conservation equation as the source terms. The two-phase model of globular equiaxed grain solidification is computed with the software Fluent by compiling UDF(user define function) to acquire the temperature field, concentration field and grain diameter[15]. Because of the symmetry of model, only the left 1/2 is computed.
3 Simulation results and analysis
Fig.3 and Fig.4 show the electromagnetic force and velocity vector induced by TMF and RMF, respectively. In this study, the maximum flow velocity is used as the criterion to characterize the intensity of the AC magnetic fields. During the following discussion, the cross-section of molten metal denotes the AB section of Fig.5. The point P locates in the middle of molten metal and point B locates in the edge of molten metal, which is far away from the AC magnetic field.
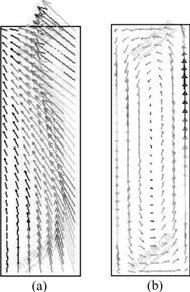
Fig.3 Electromagnetic force (a) and velocity vector (b) of molten metal with traveling magnetic field (f=50 Hz, I=20 A)
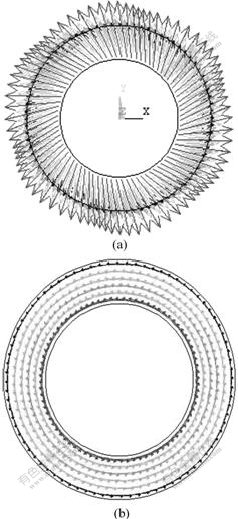
Fig.4 Electromagnetic force (a) and velocity vector (b) of molten metal with rotating magnetic field (f=50 Hz, I=40 A)
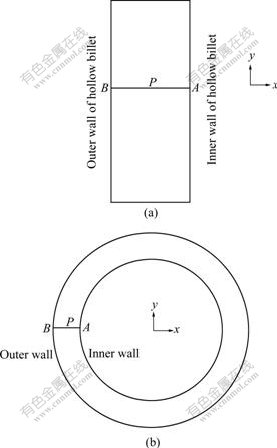
Fig.5 Schematic diagram of data acquisition: (a) With traveling magnetic field; (b) With rotating magnetic field
3.1 Effect of AC magnetic field on cooling curve
Fig.6 shows the effect of RMF on the cooling curve of Sn-3.5%Pb. During solidification of Sn-3.5%Pb, RMF can speed the heat dissipation and increase the cooling rate in the middle of molten metal, but the cooling rate at the edge of molten metal is not changed obviously. When the crystallization begins, the cooling rate in the whole cross-section of molten metal is reduced. Fig.7 shows the effect of TMF on the cooling curve of Sn-3.5%Pb. Fig.7 shows that TMF can speed up the heat dissipated and increase the cooling rate in the middle of molten metal, but the cooling rate at the edge of molten metal is decreased because of the Joule heat and circulation flow in the longitudinal section. When the crystallization begins, the cooling rate in the whole cross-section of molten metal is reduced.
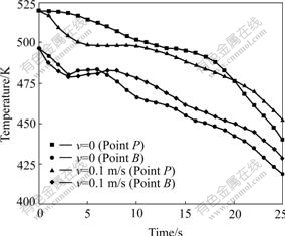
Fig.6 Effect of rotating magnetic field on cooling curve of Sn-3.5%Pb
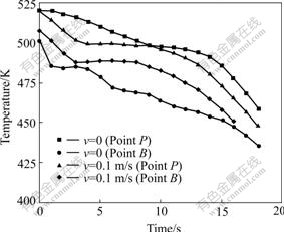
Fig.7 Effect of traveling magnetic field on cooling curve of Sn-3.5%Pb
3.2 Effect of AC magnetic field on temperature gradient
Fig.8 and Fig.9 show the temperature distribution in cross-section of molten metal with the two kinds of AC magnetic fields when the time is 10 s. It can be concluded that the two kinds of flows can reduce the temperature gradient of molten metal, and the bigger the stirring velocity, the smaller the temperature gradient.
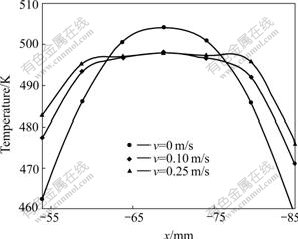
Fig.8 Effect of rotating magnetic field on temperature distribution
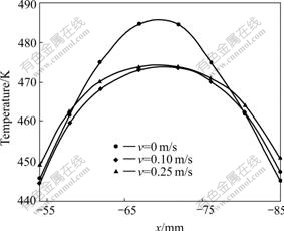
Fig.9 Effect of traveling magnetic field on temperature distribution
3.3 Effect of AC magnetic field on concentration distribution
Fig.10 and Fig.11 show the effects of AC magnetic fields on the solute concentration distribution in the cross-section of hollow billet. Both RMF and TMF can result in the macro-segregation in the hollow billet because of the non-homogeneity of flow. The stirring velocity of molten metal near the electromagnetic field is bigger than that far away from the electromagnetic field. The bigger the stirring velocity, the more serious the macro-segregation of the hollow billet. So, it can be concluded that the higher stirring velocity is very harmful to the quality of hollow billet.
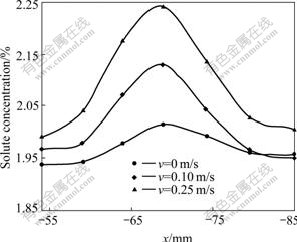
Fig.10 Effect of rotating magnetic field on solute concentration distribution of hollow billet
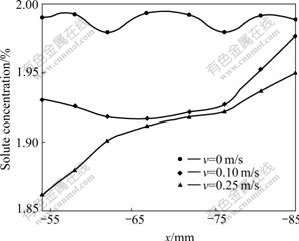
Fig.11 Effect of traveling magnetic field on solute concentration distribution of hollow billet
3.4 Effect of AC magnetic field on grain diameter
Fig.12 shows the macro-structure of hollow billet with and without stirring magnetic field (the experimental process and results are in Ref.[6]). It can be seen that the grain diameter of hollow billet is refined with the stirring magnetic field.

Fig.12 Solidification structure of hollow billet: (a) Without magnetic field; (b) With TMF (I=20 A); (c) With RMF (I=40 A)
Fig.13 shows the effect of RMF on the grain diameter of hollow billet. With the rotating magnetic field, the grain diameter in the whole cross-section of hollow billet is decreased, and the bigger the stirring velocity, the smaller the grain diameter. The reasons are as follows: 1) The circumferential flow in the transverse of molten metal increases the cooling rate in the middle of molten metal, which can increase the nucleation site of molten metal; 2) When the crystallization begins, the cooling rate and temperature gradient of molten metal are reduced, which is beneficial to facilitating the change from columnar crystals to equiaxed crystals and refining the equiaxed crystals.
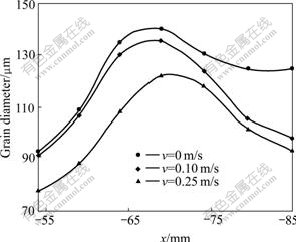
Fig.13 Effect of rotating magnetic field on grain size of hollow billet
Fig.14 shows the effect of TMF on the grain diameter of hollow billet. With the traveling magnetic field, the grain diameter in the middle of hollow billet is decreased, but the grain diameter at the edge of hollow billet is increased. The grain size in the whole cross-section of hollow billet is uniform. The reasons are as follows: 1) The axial flow in the longitudinal of molten metal increases the cooling rate in the middle of molten metal, which can increase the nucleation site of molten metal, but the cooling rate at the edge of molten metal is decreased, which can decrease the nucleation site of molten metal; 2) When the crystallization begins, both the cooling rate and temperature gradient of molten metal are reduced, which is beneficial to facilitating the change from columnar crystals to equiaxed crystals and refining the equiaxed crystals.
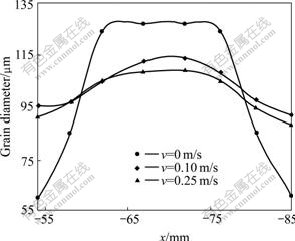
Fig.14 Effect of traveling magnetic field on grain size of hollow billet
So, in general, the bigger the stirring velocity, the smaller the grain diameter.
4 Conclusions
1) The effects of the two flows caused by TMF and RMF on the solidification process of molten metal are different. During solidification of Sn-3.5%Pb, the cooling rate in the middle of molten metal is increased with TMF and RMF. The cooling rate at the edge of molten metal is reduced with TMF and is not changed obviously with RMF. When the crystallization begins, the cooling rate in the whole cross-section of molten metal is reduced with TMF and RMF. Both TMF and RMF can reduce the temperature gradient of molten metal.
2) RMF can refine the grains in the whole cross- section of hollow billet; however, TMF makes the grains coarsen at the edge of hollow billet and makes the grain refine in the middle of hollow billet.
3) Both TMF and RMF can result in the macro- segregation in the hollow billet. The non-homogeneity of flow is the main reason for the macro-segregaion. The bigger the stirring velocity, the more serious the macro- segregation of the hollow billet.
References
[1] WANG Zhe-feng, CUI Jian-zhong, PIAO Feng-xian. Out-phase electromagnetic continuous casting of hollow billet [J]. The Chinese Journal of Nonferrous Metals, 2006, 16(3): 500-504. (in Chinese)
[2] LI Qiu-lin, LI Xin-tao, LI Ting-ju, JIN Jun-ze. Structure and property of Cu tube by horizontal electromagnetic continuous casting [J]. Rare Metal Materials and Engineering, 2006, 35(7): 1126-1128. (in Chinese)
[3] ZHANG Qi, LI Ting-ju, WANG Tong-min, JIN Jun-ze. Effect of traveling magnetic field in the inner-mold on the solidification structure of hollow billet [J]. Rare Metal Materials and Engineering, in press. (in Chinese)
[4] FLEMINGS M C. Behavior of metal Al alloys in the semisolid state [J]. Metall Trans, 1991, 22B(6): 269-293.
[5] VIVES C. Effects of forced electromagnetic vibrations during the solidification of aluminum alloys (Part I): Solidification in the presence of crossed alternating electric fields and stationary magnetic fields [J]. Metallurgical and Materials Transactions, 1996, B27: 445-455.
[6] ZHAO Zhi-hao, CUI Jian-zhong, DONG Jie, ZHANG Hai-tao, ZHANG Bei-jiang. Effect of low frequency electromagnetic field on microstructures and macrosegregation of horizontal direct chill casting aluminum alloy [J]. Trans Nonferrous Met Soc China, 2004, 14(6): 1095-1099.
[7] WILLERS B, ECKERT S, MICHEL U, HAASE I, ZOUHAR G. The columnar-to-equiaxed transition in Pb-Sn alloys affected by electromagnetically driven convection [J]. Materials Science and Engineering, 2005, A402: 55-65. (in Chinese)
[8] ECKERT S, WILLERS B, NIKRITYUK P A, ECKERT E, MICHEL U, ZOUHAR G. Application of a rotating magnetic field during directional solidification of Pb-Sn alloys: Consequences on the CET [J]. Materials Science and Engineering, 2005, A412/414: 211-216.
[9] FENG Ci-zhang. Electromagnetic field [M]. Beijing: People Education Press, 1985: 279. (in Chinese)
[10] CUI Jian-zhong. Solidification of Al alloys under electromagnetic field [J]. Trans Nonferrous Met Soc China, 2003, 13(3): 473-483.
[11] WANG Fu-jun. Computational fluid dynamic analysis [M]. Beijing: Tsinghua University Press, 2004: 7. (in Chinese)
[12] HA M Y, LEE H G, SEONG S H. Numerical simulation of three-dimensional flow, heat transfer and solidification of steel in continuous casting mold with electromagnetic brake [J]. Journal of Materials Processing Technology, 2003, 133: 322-339.
[13] WANG Tong-min, YAO Shan, ZHANG Xing-guo, JIN Jun-ze, WU M, LUDWIG A, PUSTAL B, B?HRIG-POLACZEK A. Modeling of the thermo-solutal convection, shrinkage flow and grain movement during globular equiaxed solidification in a multi-phase system (I): Three-phase flow model [J]. Acta Metallurgica Sinica, 2006, 42(6): 584-590.
[14] ANSYS Low-Frequency Electromagnetic Analysis Guide. ANSYS user’s guide [M]. ANSYS Inc, 1997: 3.1-3.8.
[15] UDF Manual. FLUENT 6.1 user’s guide [M]. Fluent Inc, 1998: 10.1-10.3.
Foundation item: Project(50274017; 50474055) supported by the National Natural Science Foundation of China; Project(20052176) supported by Natural Science Foundation of Liaoning Province, China; Project supported by Homecoming Foundation of Ministry of Education, China
Corresponding author: ZHANG Qi; Tel: +86-411-84706114; E-mail: zhangqidlut@126.com
(Edited by HE Xue-feng)