J. Cent. South Univ. Technol. (2007)03-0408-05

DOI: 10.1007/s11771-007-0080-6               

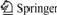
Closure behavior of rock joint under dynamic loading

WANG Wei-hua(王卫华), LI Xi-bing(李夕兵), ZHANG Yi-ping(张义平), ZUO Yu-jun(左宇军)

(School of Resources and Safety Engineering, Central South University, Changsha 410083, China)

Abstract: The normal compression tests on intact samples and artificial joints with different saw-tooth shape under cyclic loading and half-sine waves of different frequencies were performed by using Instron1342 servo-controlled material testing machine. The specimens were made artificially with mortar. The loading frequency ranged from 0.005 Hz to 0.1 Hz. The experimental results show that joint closure curves are non-linear and concave up. The stress-deformation curves under cyclic loading exhibit hysteresis and permanent set that diminish rapidly and keep constant finally on successive cycles. Normal displacement successively decreases from the joint J1 to J2, to J3 under the same normal loads regardless of frequency. Considering the loading frequency effect, normal displacement of joint J1 decreases with increasing the loading frequency except that the loading frequency is 0.05 Hz. Normal displacement of joint J2 increases with increasing the loading frequency. Normal displacement of joint J3 increases with increasing the loading frequency when the frequency ranges from 0.005 Hz to 0.05 Hz. Its normal displacement, however, becomes least when the loading frequency is 0.1 Hz.

Key words: joint closure behavior; cyclic load; surface geometry; load frequency

1 Introduction

Rock masses are full of discontinuities such as joints and fractures, which influence the mechanical properties of rock mass and control the stability of rock engineering. So plentiful and substantial research findings have been obtained by a lot of investigations on mechanical properties of rock joint carried out by domestic and oversea scholars^[1-14]. GOODMAN^[6] made laboratory measurements for joint closure as a function of normal stress on artificial fractures, and found the highly non-linearity of joint closure curves. On the basis of a large number of laboratory experiments on natural rock joints, BANDIS et al^[7] provided a hyperbolic function describing the relation of effective normal stress with joint closure and an experiential equation of joint shear strength. BARTON et al^[8] studied the strength, deformation and conductivity coupling of rock joints. COOK^[9] found the relationship between surface roughness of joint and joint deformation by laboratory experiments, and investigated the effect of joint closure on the conductivity and propagation of seismic waves across the joint. SUN^[10] researched into the stress-deformation properties of the discontinuity. XIA  et al^[11] used mathematical functions to describe the surface topography of joint and derived the theoretical model of joint closure.

However, the closure behavior of joint under dynamic load is an open question for the complexity of rock masses and transient of dynamic load^[15]. Recently the stability of rock slopes, rock foundations and underground structures built in rock masses under seismic and explosive loads is of great importance in rock engineering applications^[16-19]. Obviously exact evaluation on dynamic stability depends on understanding the mechanical behavior of rock joints under dynamic loads. In addition, this is no doubt a prerequisite input data for numerical modeling of the dynamic response of jointed rock masses which can be well analyzed by the distinct element method^[20]. In this study, the compression tests on artificial joints with regular saw-teeth shape under cyclic loads and half-sine waves of different frequencies were performed by using Instron1342 servo-controlled material testing machine. On the basis of the test results, the closure behavior of joint under dynamic loading were discussed.

2 Experimental

For a certain geometry pattern of a joint, tests will be performed under a series of strain rates to observe the strain rate effect, so it is necessary to prepare identical samples. However, it is impossible to get the natural rock joint with identical joint surfaces, so laboratory specimens were made from an artificial material so that the difficulty of the interpretation of test results on real rock joints by sample variability can be overcome, and this can also lead to the concentration on strain rate effect. A set of joint specimen includes the upper part with regular saw-tooth shape on joint surfaces and the lower part with flat planar joint surface. When carrying out tests, two parts were put together on test machine. The inclination angle of the saw-tooth was 60?, the length was 5 mm. The row number of saw-tooth is chosen to 2, 3 and 4, as shown in Fig.1. The apparent surface area of joint is 900 mm².

The total experiments were performed using the Instron1342 testing machine in Laboratory of Central South University in China. It included two parts: one part was cyclic compression tests; the other part was dynamic compression tests of joints.

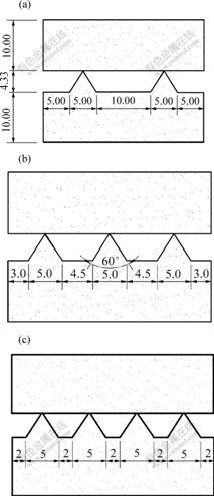
Fig.1 Configuration of saw-tooth shapes(unit: mm)

(a) Joint J1; (b) Joint J2; (c) Joint J3

 3 Results and discussion

3.1 Test results subjected to cyclic loading

Fig.2 shows the normal stress versus displacement curves of joint samples with different saw-tooth under cyclic loading. Fig.3 indicates that the area of hysteresis

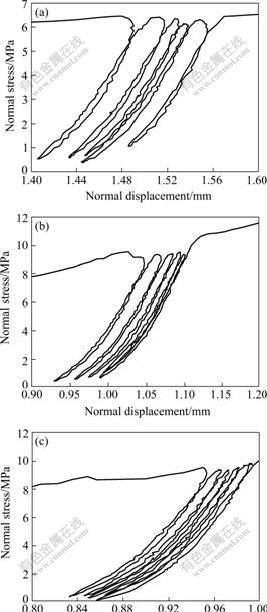
Fig.2 Normal stress vs displacement curves

(a)      Joint J1; (b) Joint J2; (c) Joint J3

Fig.3 Area of hysteresis loop vs cycle number

loop varies with the cycle number. It can be seen from Fig.2 and Fig.3 that the stress-closure curves are highly non-linear and concave up, which was observed by other scholars^[6-8], and those cycles of loading and unloading exhibit hysteresis and permanent set that diminishes rapidly and keep constant at last with successive cycles.

Joint deformation includes recoverable elastic deformation and unrecoverable plastic deformation. Fig.4 gives the relation between maximum deformation, recoverable deformation, irrecoverable deformation and cycle number.

Fig.4 Maximum, recoverable, residual deformation vs cycle number

(a)Joint J1; (b) Joint J2; (c)Joint J3

GOODMAN^[6] suggested that the non-linearity derives from the inelastic crushing and splitting of asperities. This is contrary to SUN’s suggestion that the observed non-linear behavior is linear elastic deformation, which can be explained by contact theory and be validated by the joint closure test under cyclic load^[10]. Fig.4 shows that most irrecoverable permanent set derives from the first cycle. This is a result of inelastic crushing and splitting at the peak asperities of contact that can not be recovered on unloading. Joint produces closure after crushing of peak asperities, and the second peak asperities of surface wall contacts, which results in increasing the contacts areas and the number of contacts as the normal stress increases, so the closure-stress curve shows elastic and recoverable non-linearity under successive cycles.

It can be concluded that GOODMAN’s and SUN’s suggestions of non-linear stress-deformation behavior of joint are reasonable, but their suggestions only described the joint closure behavior accurately at a certain stage. It is the authors’ view that the crushing of asperities accounts more for hysteresis and irrecoverable joint deformation during the first cycle, but non-linear deformation at successive cycles is attributed to non-linear elastic deformation.

3.2 Test results under half-sine waves of different frequencies

3.2.1 Relation between loading frequency and average strain rate

First, relation between loading frequency and strain rate was explored. Different levels of loading frequency from 0.005 to 0.1 Hz were applied on different identical jointed samples. Based on the curve of normal closure deformation behavior, the average strain rate can be calculated. The resulting responses of loading frequencies versus average strain rate are shown in Fig.5. As can be seen from Fig.5, there are linear trends for loading frequency with average strain rate. It can be concluded that the loading frequency has the same effect with strain rate in the present study, so it is feasible to control the strain rate by changing the loading frequency.

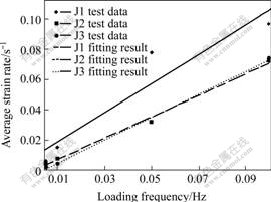
Fig.5 Average strain rate vs loading frequency

3.2.2 Effect of row number of saw-tooth and loading frequency on closure behavior of joints

In order to obtain the deformation of joint itself, the deformation of joint walls must be subtracted from the measured total deformation of the joint specimens. Artificial joints with different row number of asperities were compressed at the half-sine waves of different frequencies. The closure curves of the joints are illustrated in Fig.6.

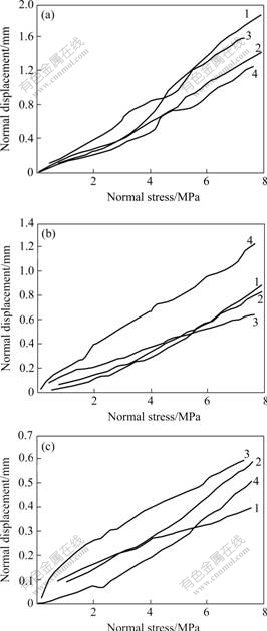
Fig.6 Closure curves of given joints at four different frequencies

1—f₁=0.005 Hz; 2—f₁=0.01 Hz; 3—f₃=0.05 Hz; 4—f₄=0.1 Hz;

(a) Joint J1; (b) Joint J2; (c) Joint J3

Fig.6 shows that the closure curves of joints with different row number of asperities are markedly different at the given frequency. The curves become a little stiffer with increasing the row number of asperities. It is because that the contact area increases when row number of asperities increases, so the normal displacement successively decreases from the joint J1 to J2, to J3 under the same normal loads.

In addition, Fig.6 shows that the closure curves under the half-sine waves of different loading frequencies are markedly different for identical joint samples. That is to say, loading frequency has significant effect on the closure behavior of the joint, regardless of joint surface geometry. Normal displacement of joint J1 decreases with increasing the load frequencies under the same loads except that the loading frequency is 0.05 Hz. Normal displacement of joint J2 increases with increasing the load frequencies under the same loads. Normal displacement of joint J3 increases with increasing the loading frequencies when the frequency ranges from 0.005 Hz to 0.05 Hz. However, its normal displacement becomes least when the loading frequency is 0.1 Hz.

4 Conclusions

1) The stress-deformation curve is highly non-linear and concave up. The most permanent deformation at the beginning derives from the inelastic crushing of the peak asperities; subsequently the non-linearity is attributed to elastic and recoverable non-linear deformation.

2) The stress-deformation curve of cyclic compression test exhibits hysteresis and permanent set that diminish rapidly and keep constant finally on successive cycles. The irrecoverable deformation increases with the increasing cycles, but the most irrecoverable deformation occurs on the first cycle.

3) At the frequency range used in the present test, relationship between average strain rate and loading frequency is linear and average strain rate increases with increasing loading frequency, so the average strain rate can be controlled equivalently by changing the loading frequency.

4) The row number of saw-tooth has significant effect on closure behavior of the joint. Normal displacement successively decreases from the joint J1 to J2, to J3 under the same normal loads, regardless of load frequency.

5) Loading frequency influences markedly the joint closure behavior. Normal displacement decreases with increasing loading frequencies for the joint J1 under the same loads except that the loading frequency is 0.05 Hz. Normal displacement increases with increasing loading frequencies for the joint J2. For the joint J3, normal displacement increases with increasing loading frequencies when the frequency ranges from 0.005 Hz to 0.05 Hz. However, normal displacement becomes least when the loading frequency is 0.1 Hz.

References

[1] JAFARI M K, AMINI HOSSEINI K, PELLET F, et al. Evaluation of shear strength of rock joints subjected to cyclic loading[J]. Soil Dynamics and Earthquake Engineering, 2003, 23(1): 619-630.

[2] HUTSON R W, DOWDING C H. Joint asperity degradation during cyclic shear[J]. International Journal of Rock Mechanics and Mining Science & Geomechanics Abstract, 1990, 27(2): 109-119.

[3] BARBERO M, BARLA G, ZANINETTI A. Dynamic shear strength of rock joints subjected to impulse loading[J]. International Journal of Rock Mechanics and Mining Science & Geomechanics Abstract, 1996, 33(2): 505-575.

[4] HSIUNG S M, GHOSH A, CHOWDHURY A H, et al. Laboratory investigation of rock joint dynamic behavior[C]// Rossmanith ed. Mechanics of Jointed and Faulted Rock. Rotterdam: Balkema, 1995: 484-488.

[5] BARLA G, BARBERO M, SCAVIA C, et al. Direct shear testing of single joints under dynamic loading[C]// Barton, Stephansson ed. Rock Joints. Rotterdam: Balkema, 1990: 447-454.

[6] GOODMAN R E. Methods of Geological Engineering in Discontinuous Rocks[M]. West New York, 1976.

[7] BANDIS S C, LUMSDEN A C, BARTON N R. Fundamentals of rock joint deformation[J]. International Journal of Rock Mechanics and Mining Science & Geomechanics Abstract, 1983, 20(6): 249-268.

[8] BARTON N R, BANDIS S C, BAKHTAR K. Strength, deformation and conductivity coupling of rock joints[J]. International Journal of Rock Mechanics and Mining Science & Geomechanics Abstract, 1985, 22(3): 121-140.

[9] COOK N G W. Natural joints in rock: mechanical, hydraulic and seismic behavior and properties under normal stress[J]. International Journal of Rock Mechanics and Mining Science & Geomechanics Abstract, 1992, 29(3): 198-223.

[10] SUN Z Q. A study on stress and deformation properties of discontinuous planes[J]. Chinese Journal of Rock Mechanics and Engineering, 1978, 6(4): 287-300. (in Chinese)

[11] XIA C C, YUE Z Q, THAM L G, et al. Quantifying topography and closure deformation of rock joints[J]. International Journal of Rock Mechanics & Mining Science, 2003, 40(2): 197-220.

[12] MALAMA B, KULATILAKE P H S W. Models for normal fracture deformation under compressive loading[J]. International Journal of Rock Mechanics & Mining Science, 2003, 40(6): 893-901.

[13] HOPKINS D L. The implication of joint deformation in analyzing the properties and behavior of fractured rock mass underground excavations and faults[J]. International Journal of Rock Mechanics and Mining Science, 2000, 37(1): 175-202.

[14] PYRAK-NOLTE L J, MORRIS J P. Single fractures under normal stress: the relation between fracture specific stiffness and fluid flow[J]. International Journal of Rock Mechanics and Mining Science, 2000, 37(1/2): 245-262.

[15] CAI J G, ZHAO J, LI H B. Effects of loading rate on fracture normal behavior[C]// WAG S J, FU B J, LI Z K, ed. Frontiers of Rock Mechanics and Sustainable Development in the 21st Century. Rotterdam: A. A. Balkema, 2001: 1997-1200.

[16] DHAWAN K R, SINGH D N, GUPTA I D. Dynamic analysis of underground openings[J]. Rock Mechanics and Rock Engineering, 2004, 37(4): 299-315.

[17] KUMSAR H, AYDAN O, ULUSAY R. Dynamic and static stability assessment of rock slopes against wedge failures[J]. Rock Mechanics and Rock Engineering, 2000, 33(1): 31-51.

[18] CHEN J Y, HU Z Q, LIN G. 3D seismic response study on large scale underground group caverns[J]. Chinese Journal of Geotechnical Engineering, 2001, 23(4): 494-498. (in Chinese)

[19] ZHANG J C. Vibration characteristics of blasting in bed rock mass at Sanxia Project[J]. Explosion and Shock Waves, 2001, 21(2): 131-137. (in Chinese)

[20] Itasca. Three Dimensional Distinct Element Codes: Optional Features[M]. Minneapolis: Itasca Consulting Group, Inc, 2003.

(Edited by YUAN Sai-qian)

Foundation item: Projects(50490274; 50490272) supported by the National Natural Science Foundation of China; Project(2002CB412703) supported by the National Basic Research Program of China

Received date: 2006-09-24; Accepted date: 2006-12-27

Corresponding author: WANG Wei-hua, PhD; Tel: +86-731-8836628, 13873165624; E-mail: csuwwh@126.com