J. Cent. South Univ. Technol. (2011) 18: 36-41
DOI: 10.1007/s11771-011-0655-0
Hot deformation behavior and constitutive relationship of Q420qE steel
YU Bao-jun(禹宝军)1, 2, GUAN Xiao-jun(关小军)1, 2, WANG Li-jun(王丽君) 1, 2,
ZHAO Jian(赵健)1, 2, LIU Qian-qian(刘千千)1, 2, CAO Yu(曹宇)1, 2
1. Key Laboratory for Liquid-Solid Structural Evolution and Processing of Materials (Ministry of Education),
Shandong University, Ji’nan 250061, China;
2. School of Materials Science and Engineering, Shandong University, Ji’nan 250061, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2011
Abstract: Isothermal compression tests at temperatures from 1 273 to 1 423 K and strain rates from 0.1 to 10 s-1 were carried out to investigate the flow behaviors of Q420qE steel. Stress-strain data collected from the tests were employed to establish the constitutive equation, in which the influence of strain was incorporated by considering the effect of strain on material constants Q, n, α, and ln A. The results show that the flow stress curves are dependent on the strain, strain rate and deformation temperature. They display typical dynamic recrystallization behavior and consist of three stages, i.e., hardening stage, softening stage and steady stage. The flow stress decreases with increasing the deformation temperature and decreasing the strain rate. In addition, the flow stress data predicted by the proposed constitutive model agree well with the corresponding experimental results, and the correlation coefficient and the average absolute relative error between them are 0.990 3 and 3.686%, respectively.
Key words: Q420qE; bridge steel; hot compression; flow stress; strain dependent constitutive equation
1 Introduction
The understanding of metals and alloys behavior under hot working condition has a great importance to designers of metal forming processes because it can affect the required energy as well as the microstructure changes of deformed metal through work hardening (WH), dynamic recovery (DRV) and dynamic recrystallization (DRX) [1-4]. Constitutive equation, which relates to the stress, strain, strain rate and deformation temperature, is a powerful tool to describe material behavior during hot deformation. Therefore, a number of constitutive equations were available to model the flow curves under hot working conditions in recent years. CINGARA and McQUEEN [5] developed the hyperbolic sine constitutive equation that was introduced by GARAFALO to express elevated temperature flow behavior. McQUEEN and RYAN [6] gave a comprehensive review on constitutive relationships in hot working of austenitic stainless steels, carbon and alloying steels and Al alloys. SLOOF et al [7] introduced a strain-dependent parameter into the sine hyperbolic constitutive equation to predict the flow stress of Mg-Al4-Zn1 alloy. ZHAN et al [8], LIN et al [9] and MANDAL et al [10] employed a revised sine hyperbolic constitutive equation incorporating strain dependent term to predict elevated temperature flow behavior of porous FVS0812 aluminum alloy, 42CrMo steel and Ti-modified austenitic stainless steel.
Q420qE (American grade: ASTM Gr. 60 [415]) is one of the typical domestic bridge steels. Due to its good balance of strength, toughness, weldability and corrosion resistance, Q420qE steel is widely used in bridge construction. However, the investigations have been mainly focused on the alloy composition, heat treatment process, fatigue resistance and weldability of Q420qE steel, and little attention has been paid on the hot deformation behavior of this important engineering material [11-12]. In the present study, the effects of the deformation temperature, strain rate and strain on flow behavior of Q420qE steel were investigated, and a strain dependent constitutive equation which could predict the flow stress evolutions was established. Comparisons of experimental and predicted results of flow stress were conducted. The present work is helpful in optimizing thermo-mechanical parameters and providing proper stress-strain relationship for numerical simulations of Q420qE steel.
2 Experimental
Commercial Q420qE steel with chemical composition (mass fraction, %) of 0.08 C, 0.21 Si, 1.37 Mn, 0.009 P, 0.003 S, 0.26 Ni, 0.21 Cu, 0.058 Nb, 0.030 Ti and balance Fe was employed in the experiment. Cylindrical specimens, with 10 mm in diameter and 15 mm in height, were machined with their axes aligned along the rolling direction.
The single pass hot compression tests were carried out on a MMS-300 thermo-mechanical simulator. In order to minimize the effect of frictions between the specimens and the die on flow stress, the ends of the specimens were coated with lubricant (graphite mixed with machine oil). The specimens were heated to 1 473 K at 20 K/s and held for 5 min for homogenization, then cooled down to the test temperatures at 10 K/s. The test temperatures were 1 273, 1 323, 1 373 and 1 423 K, respectively. After being held for 1 min for heat balance at the test temperature, the specimens were deformed to a strain of 0.8 at strain rates of 0.1, 1, 3 and 10 s-1. The stress-strain curves were obtained from the load- displacement data.
3 Results and discussion
3.1 Stress-strain curves
Typical flow stress-strain curves for Q420qE steel are illustrated in Fig.1. As shown in Fig.1, the effects of the deformation temperature and strain rate on the flow stress are obvious. The stress level decreases with increasing the deformation temperature and decreasing the strain rate, which gives an evidence that the dynamic softening is extensive at higher temperatures and lower strain rates. The reason could be that higher temperature offers higher driving force for grain-boundary migration, and lower strain rate provides longer time for energy accumulation and nucleation and growth of dynamically recrystallized grains [10].
In addition, the dependence of stress-strain curves on strain can be seen from Fig.1. Due to the combined effects of WH, DRV and DRX, with increasing the strain, all the stress-strain curves obtained from the compression tests exhibit hardening stage, softening stage and steady stage [1, 13-14]. The curves display a rapid initial increase, which is due to the predominance of WH. After the attainment of a critical strain, the curves experience a peak point, characterized by a peak strain and a corresponding peak stress, which is associated with the development of DRV and DRX. Meanwhile, an increase in the peak stress with decreasing the deformation temperature and increasing the strain rate can be seen. At large strains, a steady stage appears due to the balance among WH, DRV and DRX. The flow behavior is totally dependent on the state of dislocation density in the material. Dislocation density is
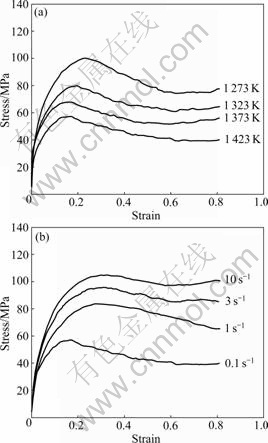
Fig.1 True stress-true strain curves of Q420qE steel under various deformation conditions: (a)  0.1 s-1; (b) T=1 423 K
0.1 s-1; (b) T=1 423 K
controlled by two competing processes: continuous generation due to the intersection and tangle of dislocations, leading to an accumulation of WH, and gradual annihilation due to the cross-slip and climb of dislocation, leading to a dynamic softening effect. In the initial stage of deformation, the flow stress increases with increasing the strain because the level of the dislocation generation is much larger than that of the dislocation annihilation. As the deformation progresses, the effect of the dynamic softening is enhanced due to the increase of slip systems, resulting in a slow descent of the flow stress after the attainment of the peak stress.
3.2 Constitutive equation for Q420qE steel
The hyperbolic sine function described for the Zener-Hollomon parameter can be used for flow stress calculation at high temperatures [5-7, 15]:
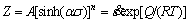 (1)
(1)
where A, n and α are material constants; Q is the activation energy for deformation; R is gas constant and given the value of 8.314 J/(mol?K); and T is the deformation temperature.
It is worth emphasizing that the equation is usually employed to characterize the peak stress or the steady-state stress, which can only describe the impacts of strain rate and deformation temperature on the peak stress or steady-state one but not the whole flow behavior. Moreover, strain, an important parameter during hot deformation process of metals, does not play any role in this equation. In the present work, in order to incorporate the influence of strain on flow stress of Q420qE steel, the material constants, e.g. Q, n, α, and ln A, are assumed to be polynomial functions of strain [9-10], i.e.,
 (2)
(2)
where the values of Q, n, α, and ln A are evaluated at various strains within the range of 0.05-0.8 at an interval of 0.05; k, the order of polynomial functions in Eq.(2), is to be determined.
3.2.1 Determination of material constants
Experimental stress-strain data under different deformation conditions were used to determine the values of material constants. For all strains, the procedures of determining the material constants are the same. Here, the strain of 0.4 is taken as an example.
The favorite equations for hot deformation at low stress level and high stress level are the power law and the exponential law, respectively [5-6, 15-16]:
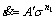 (3)
(3)
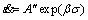 (4)
(4)
where A′, n1, A″ and β are materials constants. As known, Eq.(1) approximately degenerates into Eq.(3) at low stress level and it approximately approaches to Eq.(4) at high stress level through Taylor series expansion [16]; so, it covers all levels of stress. By recognition of the relationship among α, n1 and β, i.e., α=β/n1 [6], the constant α in Eq.(1) can be determined.
Taking the natural logarithm on both sides of Eqs.(3) and (4), the values of β and n1 can be obtained from the slopes of the fitting lines on 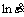 -σ and
-σ and 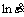 -ln σ plots, respectively, as shown in Fig.2. Because the lines are parallel to each other, the mean values of β and n1 are calculated as 0.067 01 MPa-1 and 5.145 7, respectively. Then, α=β/n1=0.013 02 MPa-1.
-ln σ plots, respectively, as shown in Fig.2. Because the lines are parallel to each other, the mean values of β and n1 are calculated as 0.067 01 MPa-1 and 5.145 7, respectively. Then, α=β/n1=0.013 02 MPa-1.
For all stress levels, taking logarithm on both sides of Eq.(1), it follows
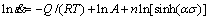 (5)
(5)
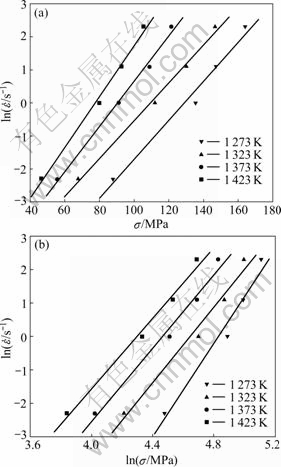
Fig.2 Relationships between strain rate and flow stress at ε=0.4: (a) 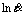 -σ; (b)
-σ; (b) 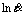 -ln σ
-ln σ
By assuming that T and  are constants, differentiating Eq.(5) gives
are constants, differentiating Eq.(5) gives
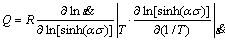 (6)
(6)
Based on the slopes of fitting lines under the employed deformation conditions in  -ln[sin(ασ)] and ln[sin(ασ)]-T plots, as shown in Figs.3(a) and (b), the values of the last two terms at the right side of Eq.(6) are measured as 3.856 5 and 10.520 3, respectively. Then, Q and A can be obtained as 337.31 kJ/mol and 1.53×1012 s-1 from Eq.(6) and Eq.(5), respectively.
-ln[sin(ασ)] and ln[sin(ασ)]-T plots, as shown in Figs.3(a) and (b), the values of the last two terms at the right side of Eq.(6) are measured as 3.856 5 and 10.520 3, respectively. Then, Q and A can be obtained as 337.31 kJ/mol and 1.53×1012 s-1 from Eq.(6) and Eq.(5), respectively.
3.2.2 Strain-dependent constitutive equation
The values of material constants of Q420qE steel at different deformation strains are presented in Fig.4. As can be observed from Figs.4(a), (b) and (d), the variation tendency of Q, n and lnA is almost the same. With increasing the strain, they experience a rapid initial decrease, and a slow increase at higher strain levels. However, α experiences a quick decrease and increase, then keeps stable at large strain levels, which is different from the variations of Q, n and ln A. It should be pointed out that the change of the activation energy may reflect
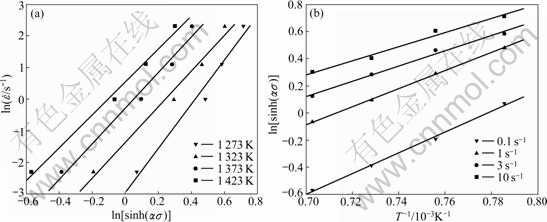
Fig.3 Curves of  -ln[sinh(ασ)] (a) and ln[sinh(ασ)]-T -1 (b) at ε=0.4
-ln[sinh(ασ)] (a) and ln[sinh(ασ)]-T -1 (b) at ε=0.4
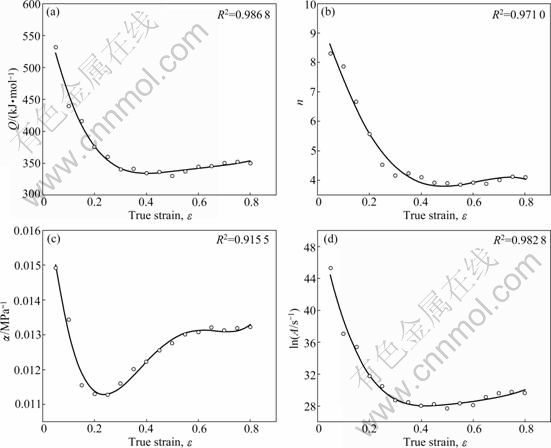
Fig.4 Relationships between material constants and true strain: (a) Q-ε; (b) n-ε; (c) α-ε; (d) ln A-ε
the role of DRX during hot deformation. At lower strain levels, the dislocation movement gets easier due to the development of DRX, while at higher strain levels, the dislocation movement becomes harder because of the effect of DRX on grain refinement [16].
Analysis indicates that the relationships between material constants Q, n, α, ln A and strain ε can be well fitted by fourth order polynomials through the least square method, as shown in Fig.4 (solid line). The fitted functions are given as
Q=610.882 8-2 003.763 3 ε+5 244.331 8 ε2-5 881.775 9 ε3+2 444.268 6 ε4 (7)
n=10.040 8-30.276 42 ε+42.378 0 ε2-7.222 9 ε3-12.692 2 ε4 (8)
α=0.018 03-0.072 46 ε+0.261 5 ε2-0.360 2 ε3+0.171 6 ε4 (9)
ln A=51.887 2-169.746 6 ε+ 438.579 7 ε2-490.561 4 ε3+205.976 4 ε4 (10)
From Eq.(1), the flow stress can be represented as a function of strain, strain rate and deformation temperature, which follows
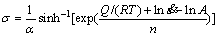 (11)
(11)
where the values of Q, n, α and ln A are determined by Eqs.(7)-(10), respectively.
3.2.3 Verification of constitutive equation
Fig.5 shows the comparisons between the stress- strain curves predicted by the established constitutive equations and corresponding experimental results for different deformation conditions of Q420qE steel. It can be easily found that the predicted results and the experimental ones are in good agreement within the entire strain range. Then, two statistical parameters, correlation coefficient (R) and average absolute relative error (AARE, E) which are employed to quantify the accuracy [10], are expressed as
 (12)
(12)
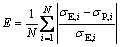 (13)
(13)
where N is the number of used flow stress data, and
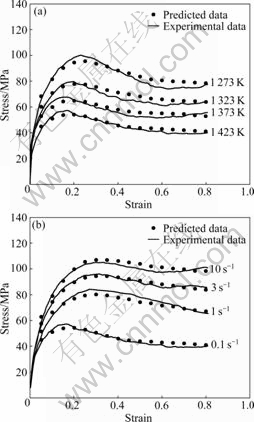
Fig.5 Comparison between experimental and predicted flow stress curves: (a)  0.1 s-1; (b) T=1 423 K
0.1 s-1; (b) T=1 423 K
N=256 in this study. σE and σP are the experimental stress and predicted stress, respectively.  and
and 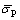 are the mean values of σE and σP.
are the mean values of σE and σP.
A good correlation between the experimental and predicted flow stress data is shown in Fig.6, where R=0.990 3. Also, AARE is obtained as 3.686% according to Eq.(13). The results indicate that Eqs.(7)-(11) provide accurate descriptions of the flow stress evolutions of Q420qE steel under various deformation conditions, and can be used as the stress-strain data of numerical simulations.
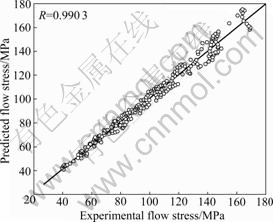
Fig.6 Correlation between experimental and predicted flow stress data
4 Conclusions
1) The stress-strain curves obtained from compression tests in the temperature range of 1 273- 1 423 K and strain rate range of 0.1-10 s-1 for Q420qE steel indicate that the flow stress is sensitive to the strain, deformation temperature and strain rate. The flow behavior is essentially dependent on the competition between dislocation generation and annihilation.
2) A strain-dependent constitutive equation is establised to describe the flow stress evolutions of Q420qE steel. The proposed constitutive equation can be expressed as
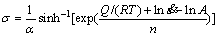
where
Q=610.882 8-2 003.763 3 ε+5 244.331 8 ε2-5 881.775 9 ε3+2 444.268 6 ε4,
n=10.040 8-30.276 42 ε+42.378 0 ε2-7.222 9 ε3-12.692 2 ε4,
α=0.018 03-0.072 46 ε+0.261 5 ε2-0.360 2 ε3+0.171 6 ε4,ln A=51.887 2-169.746 6 ε+ 438.579 7 ε2-490.561 4 ε3+205.976 4 ε4.
References
[1] ABBASI S M, SHOKUHFAR A. Prediction of hot deformation behaviour of 10Cr-10Ni-5Mo-2Cu steel [J]. Materials Letters, 2007, 61(11/12): 2523-2526.
[2] SERAJZADEH S. A mathematical model for evolution of flow stress during hot deformation [J]. Materials Letters, 2005, 59(26): 3319-3324.
[3] LIAO Shu-lun, ZHANG Li-wen, YUE Chong-xiang, PEI Ji-bin, GAO Hui-ju. Hot deformation behaviors and flow stress model of GCr15 bearing steel [J]. Journal of Central South University of Technology, 2008, 15(5): 575-580.
[4] WANG Jin, CHEN Jun, ZHAO Zhen, RUAN Xue-yu. Hot deformation behavior and flow stress model of F40MnV steel [J]. Journal of Central South University of Technology, 2007, 14(1): 19-23.
[5] CINGARA A, McQUEEN H J. New method for determining sinh constitutive constants for high temperature deformation of 300 austenitic steels [J]. Journal of Materials Processing Technology, 1992, 36(1): 17-30.
[6] McQUEEN H J, RYAN N D. Constitutive analysis in hot working [J]. Materials Science and Engineering A, 2002, 322(1/2): 43-63.
[7] SLOOFF F A, ZHOU J, DUSZCZYK J, KATGERMAN L. Constitutive analysis of wrought magnesium alloy Mg-Al4-Zn1 [J]. Scripta Materialia, 2007, 57(8): 759-762.
[8] ZHAN M Y, CHEN Z H, ZHANG H, XIA W J. Flow stress behavior of porous FVS0812 aluminum alloy during hot-compression [J]. Mechanics Research Communications, 2006, 33(4): 508-514.
[9] LIN Y C, CHEN M S, ZHANG J. Constitutive modeling for elevated temperature flow behavior of 42CrMo steel [J]. Computational Materials Science, 2008, 42(3): 470-477.
[10] MANDAL S, RAKESH V, SIVAPRASAD P V, VENUGOPAL S, KASIVISWANATHAN K V. Constitutive equations to predict high temperature flow stress in a Ti-modified austenitic stainless steel [J]. Materials Science and Engineering A, 2009, 500(1/2): 114-121.
[11] WANG Lei, GAO Cai-ru, WANG Yan-feng, DU Lin-xiu, ZHAO De-wen, LIU Xiang-hua. Development of Bridge Steels in China [J]. Materials for Mechanical Engineering, 2008, 32(5): 1-3. (in Chinese)
[12] QU Zhan-yuan, MA Jian-po, XU Ke. Fracture resistance of Q420 steel and its welding joint [J]. Journal of Mechanical Strength, 2008, 30(4): 668-672. (in Chinese)
[13] YUE Chong-xiang, ZHANG Li-wen, LIAO Shu-lun, PEI Ji-bin, GAO Hui-ju, JIA Yuan-wei, LIAN Xiao-jie. Research on the dynamic recrystallization behavior of GCr15 steel [J]. Materials Science and Engineering A, 2009, 499(1/2): 177-181.
[14] EBRAHIMI R, ZAHIRI S H, NAJAFIZADEH A. Mathematical modelling of the stress–strain curves of Ti-IF steel at high temperature [J]. Journal of Materials Processing Technology, 2006, 171(2): 301-305.
[15] SELLARS C M, TEGART W J M. Hot workability [J]. International Metallurgical Reviews, 1972, 17(1): 1-24.
[16] WANG Zhi-xiang, LIU Xue-feng, XIE Jian-xin. Constitutive relationship of hot deformation of AZ91 magnesium alloy [J]. Acta Metallurgica Sinica, 2008, 44(11): 1378-1383. (in Chinese)
(Edited by YANG Bing)
Foundation item: Project(200804220021) supported by the Specialized Research Fund for Doctoral Program of Higher Education of China; Project (Y2007F06) supported by the Natural Science Foundation of Shandong Province, China
Received date: 2009-12-17; Accepted date: 2010-03-15
Corresponding author: GUAN Xiao-jun, Professor, PhD; Tel: +86-531-81696587; E-mail: guanxj2003@126.com