DOI: 10.11817/j.issn.1672-7207.2016.08.035
单箱室波形钢腹板梁桥横向弯矩计算方法
黎雅乐1, 2,杨丙文3,张建东1, 4
(1. 东南大学 土木工程学院,江苏 南京,210096;
2. 南京航空航天大学 金城学院,江苏 南京,211156;
3. 江苏省建筑工程质量检测中心有限公司, 江苏 南京,210028;
4. 江苏省交通科学研究院股份有限公司,江苏 南京,211112)
摘要:为较简便地设计出波形钢腹板箱梁(BSW)桥的桥面板,基于框架分析法的基本原理,结合波形钢腹板箱梁的结构特点和力学特性,建立适用于单箱室波形钢腹板箱梁桥桥面板横向弯矩的计算方法,再对波形钢腹板箱梁和混凝土腹板箱梁在相同荷载作用下顶板的横向弯矩进行对比,对几座代表性的单箱室波形钢腹板箱梁桥顶板横向弯矩进行计算分析。研究结果表明:波形钢腹板箱梁桥的桥面板最大横向弯矩远高于同类混凝土腹板箱梁的横向弯矩峰值,提出的单箱波形钢腹板箱梁桥顶板横向设计弯矩的建议值可为今后同类波形钢腹板箱梁桥顶板尺寸拟定及配筋设计提供参考。
关键词:波形钢腹板箱梁(BSW);框架分析法;箱梁顶板;横向弯矩
中图分类号:U448.36 文献标志码:A 文章编号:1672-7207(2016)08-2802-08
Transverse moment of PC single box-girder bridge with corrugated steel webs
LI Yale1, 2, YANG Bingwen3, ZHANG Jiandong1, 4
(1. Department of Civil Engineering, Southeast University, Nanjing 210096, China;
2. Jincheng College, Nanjing University of Aeronautics and Astronautics, Nanjing 211156, China;
3. Jiangsu Construction Engineering Quality Test Center, Nanjing 210028, China;
4. Jiangsu Transportation Institute, Nanjing 211112, China)
Abstract: In order to simplify the design of the deck of box-girder with corrugated steel webs(BSW), a practical analytic method was presented to analyse the transverse moment of BSW based on frame analysis method and its characteristics. The comparisons of the transverse moment of BSW and box-girder with concrete webs(BCW) were carried out. The transverse moment was calculated using several representative BSW bridge examples. The results show that the maximum transverse moment of BSW is much larger than that of BCW. And the suggestion of design moment of deck in the mid span of BSW can serve as references for upper flange design of BSW.
Key words: box-girder with corrugated steel webs(BSW); frame analysis method; upper flange; transverse moment
波形钢腹板箱梁桥发源于法国,由于结构自身的优点,该桥型已在世界各地得到广泛应用[1]。自2005年国内建成首座波形钢腹板PC箱梁桥——淮安长征人行桥至今,国内已建和在建的波形钢腹板PC组合箱梁桥已超过30座[2]。各国学者对该类结构的抗弯[3-4]、抗扭[5-7]、抗剪[8-10]和结构稳定性[11-12]等方面已取得了较多研究成果,但对桥面板局部荷载作用下的受力特性和横向内力分析方法的研究较少,箱梁的横向刚度通常都小于纵向刚度,而波形钢腹板箱梁由于其截面抗畸变性能较弱[13],其桥面板横向内力与混凝土箱梁存在较大差异。已有的波形钢腹板箱梁桥面板的研究多集中在多箱室梁横向分布系数[14]和最不利位置[15]、箱梁顶板有效分布宽度[16-17]等方面。目前,国内在初步设计时对于波形钢腹板箱梁的顶板合理厚度及横向配筋设计没有明确依据。我国的波形钢腹板箱梁(BSW)桥的设计常参考国外已建桥梁或通过电算再依照混凝土桥梁设计规范[18]进行复核,常规桥梁设计软件如桥梁博士等对箱梁横向受力无法准确模拟,黄浩等[19]在迈达斯软件中实现了基于梁单元框架模型的横向内力计算,但专业设计软件多为“黑箱”,软件中波形钢腹板箱梁结构计算模块发展时间较短,是否能准确地仿真波形钢腹板与顶底板之间的约束关系值得探讨。若依靠通用有限元软件进行设计验算,则耗时较长且后处理繁琐。在初步设计阶段,急需一种横向内力的手算方法。本文作者基于框架分析法的基本原理,建立适合于单箱室波形钢腹板箱梁桥顶板横向弯矩计算方法。
1 波形钢腹板箱梁框架分析法分析
框架分析法是将箱梁的空间三维问题简化为平面框架问题进行求解的一种方法,其原理是:在箱梁的纵向取单位长度的框架,保证框架与整个箱梁体的变形相协调的前提下采用结构力学方法进行分析[18]。在分析平面框架时,需要引入适当的支承条件,如图1所示。由于这些虚加的支承条件并不存在,所以它们所产生的作用将用与支承反力大小相等但方向相反的力消除。令这些力为qi=Ri(i=1,2,3,4),如图2所示,并可分解为对称荷载qsym与反对称荷载qs和qh。正对称荷载作用下截面的横向弯矩影响较小可忽略,因此,释放支承可视为对原箱梁结构施加反对称荷载。因此,可认为箱梁的横向弯矩为加支撑框架的弯矩与反对称无支撑框架的弯矩的叠加。加支撑框架的弯矩可用弯矩分配法等结构力学方法求得,而对于波形钢腹板箱梁截面而言,反对称无支撑框架的弯矩的计算有待进一步分析。

图1 支承形式
Fig. 1 Support type of frame
1.1 内力平衡关系
在反对称荷载作用下箱梁会产生畸变,畸变翘曲应力在横截面上呈线性分布,如图3所示。设角点A由畸变产生的翘曲应力为 ,角点D由畸变产生的翘曲应力为
,角点D由畸变产生的翘曲应力为 ,其比值为
,其比值为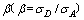 。这些翘曲应力在组成箱梁的各板平面内形成畸变内力矩,由于波形钢腹板纵向弹性模量较小,在波形钢腹板箱梁中,一般认为腹板不承担弯矩,设顶板、底板、腹板的畸变内力矩分别为
。这些翘曲应力在组成箱梁的各板平面内形成畸变内力矩,由于波形钢腹板纵向弹性模量较小,在波形钢腹板箱梁中,一般认为腹板不承担弯矩,设顶板、底板、腹板的畸变内力矩分别为 ,
,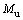 和
和 ,则:
,则:
 (1)
(1)
 (2)
(2)
 (3)
(3)
式中: ;β为由畸变内力矩自平衡确定的系数,根据波形钢腹板箱梁内力平衡关系(Mu+Mo=0)[13],得到
;β为由畸变内力矩自平衡确定的系数,根据波形钢腹板箱梁内力平衡关系(Mu+Mo=0)[13],得到 ;to为顶板厚度;tu为底板厚度;a,b,bo和c分别为横断面上腹板长度、顶板宽度、顶板在腹板间宽度、底板在腹板间宽度,如图3所示。
;to为顶板厚度;tu为底板厚度;a,b,bo和c分别为横断面上腹板长度、顶板宽度、顶板在腹板间宽度、底板在腹板间宽度,如图3所示。

图2 荷载及其分解示意图
Fig. 2 Schematic diagram of load and its resolution

图3 顶、底板畸变翘曲应力分布
Fig. 3 Distortional normal stress distribution in upper and lower flanges
设顶板畸变剪力差为 ,底板畸变剪力差为
,底板畸变剪力差为 ,根据弯矩与剪力的关系式
,根据弯矩与剪力的关系式 ,
, ,
, 可以导出顶底板的剪力差关系为
可以导出顶底板的剪力差关系为
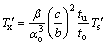 (4)
(4)
1.2 内力及位移分析
在反对称荷载作用下,顶、底板的反弯点位于中心线上,设反弯点处的剪力分别为Qs和Qx,设腹杆件反弯点处的剪力为Qh,腹板的反弯点将腹板分为上、下2段,其高度的比例为1/ηm,如图4所示。
由各角点弯矩平衡可以得到各剪力的关系[18]为:
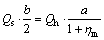 (5)
(5)
 (6)
(6)

图4 框架剪力
Fig. 4 Shear force of frame
 (7)
(7)
式中: ;
; ;
; ;根据波形钢腹板特性,将钢腹板按照刚度相等的原则换算成混凝土材料,得到等效成混凝土腹板的面外惯性矩
;根据波形钢腹板特性,将钢腹板按照刚度相等的原则换算成混凝土材料,得到等效成混凝土腹板的面外惯性矩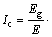
 。波形钢腹板参数如图5所示,图5中:to,tc和tu分别为上板、腹板和下板的厚度;Eg为钢板的弹性模量;E为混凝土的弹性模量;α为腹板斜板段倾角;e为波高;Lc为直板段长度;Lz为斜板段投影长度;q为波长。
。波形钢腹板参数如图5所示,图5中:to,tc和tu分别为上板、腹板和下板的厚度;Eg为钢板的弹性模量;E为混凝土的弹性模量;α为腹板斜板段倾角;e为波高;Lc为直板段长度;Lz为斜板段投影长度;q为波长。
以上得到了框架各内力中剪力的关系。框架在畸变力作用下产生畸变角和畸变位移,根据畸变角和畸变位移关系[20]可得
 (8)
(8)
其中: 波形钢腹板面内惯性矩Jh=0;混凝土顶板面内惯性矩
波形钢腹板面内惯性矩Jh=0;混凝土顶板面内惯性矩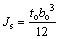 ;混凝土底板面内惯性矩
;混凝土底板面内惯性矩 ;单位荷载作用下箱梁截面的挠度参数
;单位荷载作用下箱梁截面的挠度参数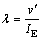 (
( 为单位荷载作用下的挠度,IE为横截面抗弯刚度)。
为单位荷载作用下的挠度,IE为横截面抗弯刚度)。
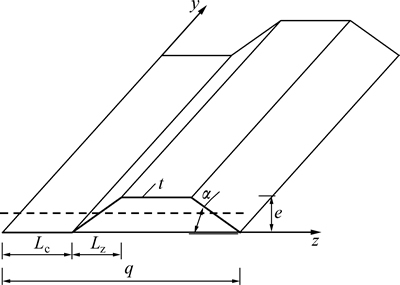
图5 波形钢腹板的形状示意图
Fig. 5 Schematic diagram of configuration of corrugated steel webs
1.3 外力、内力的平衡关系
在支承释放的反对称作用时与截面上的内力构成平衡关系,如图6所示(其中, ,
, 和
和 分别为顶板、底板和腹板扭转剪力差。
分别为顶板、底板和腹板扭转剪力差。

图6 力的平衡图示
Fig. 6 Schematic diagram of equilibrium of forces
水平力的平衡图见图6(a),水平力的平衡关系为
 (9)
(9)
竖向力的平衡如图6(b)所示,分别取框架的左、右半部,都有
 (10)
(10)
转动平衡如图6(c)所示,用框架下取两腹板交点为距心,建立转动平衡关系可以得到
 (11)
(11)
式(4)反映畸变剪力差之间关系;式(5)~(7)为各板剪力间关系式;式(8)建立起畸变剪力差与剪力间的关系。将以上关系式代入式(9)~(11),最终化为只含1个剪力、扭转剪力差和反对称力的方程式,根据扭转剪力差的关系式( )求解出剪力,最后由剪力得到反对称无支撑框架的弯矩。
)求解出剪力,最后由剪力得到反对称无支撑框架的弯矩。
2 算例及有限元验证
某跨径为30 m的单箱室波形钢腹板简支箱梁桥,箱梁顶板净宽为10.3 m,悬臂为2.36 m,腹板间距为5.58 m,箱梁中心高2.65 m。截面尺寸如图7所示。假设均布荷载q=10 kN/m作用在偏离箱梁中心线1 m的位置。

图7 波形钢腹板箱梁截面形式
Fig. 7 Cross section of BSW
设一梁段跨度等于箱梁腹板间宽度,10 kN的单位力作用在距离跨中1 m的位置。假设梁段为两端简支和两端固端2种情况,2种情况下梁段的弯矩图如图8所示。
2.1 波形钢腹板箱梁顶板横向弯矩计算
该波形钢腹板箱梁其单位长度框架梁段的截面惯性矩为:
 ;
;
 ;
;
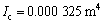
各板在平面内的截面惯性矩为:
 ;
;
 ;
;

畸变翘曲系数β=5.94。

图8 梁段弯矩图
Fig. 8 Diagram of bending moment of beam
在如图1所示的支承条件下,框架的杆端弯矩采用弯矩分配法计算得截面弯矩分布如图9所示。

图9 加支承截面弯矩分布
Fig. 9 Distribution of bending moment of cross section with support
求得支承反力:
qh=1.305 kN;
qs=-1.027 kN。
利用式(4)~(11)求得:
Qs=0.202 9 kN;
Qx=0.205 7 kN;
Qh=0.430 2 kN。
反对称荷载作用下,框架各角点弯矩为:
MA=MB=0.566 kN·m;
MC=MD=0.574 kN·m。
反对称荷载作用下截面的横向弯矩分布如图10所示。
实际箱梁的横向弯矩应由上述加支承与支承释放2种情况下的横向弯矩之和,则最终箱梁截面横向弯矩图如图11所示。

图10 反对称荷载下弯矩分布
Fig. 10 Distribution of moment of cross section under dissymmetric load
由以上计算值比较分析可知:该波形钢腹板箱梁截面顶板最大横向弯矩约为对应简支梁最大弯矩的85.8%,约为固端梁段最大正弯矩的1.89倍。

图11 横向弯矩分布
Fig. 11 Distribution of final transverse moment
2.2 对波形钢腹板箱梁横向弯矩的有限元分析
基于通用有限元软件ANSYS对上述单箱室波形钢腹板箱梁桥进行数值模拟[21],混凝土结构采用实体单元soild45,波形钢腹板采用壳单元shell63,共划分21 168个节点,14 000个单元,如图12所示。波形钢腹板与顶底板之间采用共用节点的方式进行连接,模拟实桥中无滑移剪力件的连接效果。
顶板截面横向弯矩见表1。从表1可以看出:通过推导得到的荷载作用点处桥面板横向弯矩与有限元计算值相差较小,验证了本文横向弯矩计算结果的正确性,且理论计算值比有限元值稍大,因此,用该方法手算横向弯矩最大值偏于安全。由于腹板内侧角隅处的绝对弯矩较小,角隅处相对误差偏大,但腹板内侧角隅其数值较小不控制桥面板设计,因此,不影响该方法的使用。对于角隅处而言,其最大横向弯矩应为悬臂侧而非腹板内侧,因此,其最大弯矩只与悬臂长度有关,而不受腹板形式的影响。

图12 有限元模型
Fig. 12 FE model of example
表1 顶板截面横向弯矩对比
Table 1 Comparison of transverse moment of upper flange

2.3 与同类混凝土腹板箱梁横向弯矩的比较
同类混凝土腹板箱梁(BCW)截面如图13所示,顶、底板截面尺寸及梁高与第2.1节中波形钢腹板箱梁截面相一致,其腹板由厚度为12 mm的波形钢腹板换成厚度为30 cm的混凝土腹板。2种形式箱梁的截面参数对比见表2。
表2 波形钢腹板箱梁与混凝土腹板箱梁参数对比表
Table 2 Properties comparison of BSW and BCW
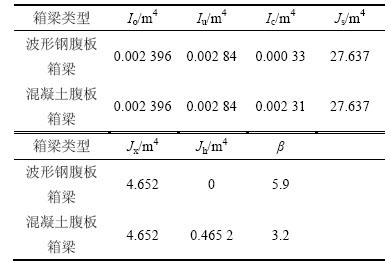
基于框架分析法,对该混凝土腹板箱梁进行横向弯矩计算,弯矩分布如图14所示。比较图14和图8可知:对于混凝土腹板箱梁,其顶板最大弯矩约为对应简支梁最大弯矩的64.1%,约为对应两端固端梁最大正弯矩的1.41倍。比较图14和图11可知:混凝土腹板箱梁桥面板最大横向弯矩是波形钢腹板顶板最大横向弯矩的74.7%。这是由于混凝土腹板的截面惯性矩远大于波形钢腹板在平面内的截面惯性矩,使混凝土腹板箱梁的腹板对顶板的约束接近于固结,而波形钢腹板箱梁腹板对顶板的约束接近于简支。

图13 混凝土腹板箱梁截面图
Fig. 13 Cross section of BCW

图14 混凝土腹板箱梁截面横向弯矩
Fig. 14 Transverse moment of BCW
3 波形钢腹板箱梁桥横向弯矩设计建议
在桥面板初步设计中,工程师常参照规范[18]中4.1.2进行桥面板配筋,对于波形钢腹板箱梁桥而言,该条款的适用性值得商榷。为了在桥面板初步设计中能够快速估算配筋量,根据前面推导得到的波形钢腹板横向弯矩计算公式,对3座国内外已建的具有代表性的单箱室波形钢腹板箱梁桥进行桥面板横向弯矩分析。以箱梁的跨中截面和根部截面为例,在截面的顶板中心线处加载100 kN集中力,计算集中力作用下桥面板最大横向弯矩(位于顶板跨中),并与跨中同样作用100 kN集中力的简支梁跨中弯矩进行对比(梁段跨径等于桥面板计算跨径即波形钢腹板中心的间距),如表3所示。
由表3可知:波形钢腹板箱梁横向最大弯矩为对应荷载作用下简支梁跨中最大弯矩的80%~90%,为安全起见,在波形钢腹板箱梁桥的设计中,建议在单箱波形钢腹板箱梁的桥面板弯矩简化计算时采用如下公式:
对跨中弯矩, (12)
(12)
对支点弯矩, (13)
(13)
式中:Mj为与计算跨径相同的简支板跨中弯矩。
表3 单箱波形钢腹板箱梁桥计算模型跨中弯矩比较
Table 3 Comparison of transverse moment of deck in mid-span of single BSW

日本本谷桥的桥面板设计[22]即采用90%的简支板弯矩作为跨中设计弯矩。由于支点角隅最大弯矩只与悬臂长度有关,而不受腹板形式的影响,故取与普通预应力混凝土箱梁的支点横向弯矩相同的设计值[18],即为简支单位宽板条跨中弯矩的70%作为其设计弯矩。
4 结论
1) 根据波形钢腹板箱梁腹板基本不承担纵向弯矩的特点,建立了适用于单箱室波形钢腹板箱梁桥顶板横向弯矩的计算方法并通过有限元分析验证其正确性和适用性。
2) 波形钢腹板箱梁与混凝土腹板箱梁相比,由于波形钢腹板的横向抗弯刚度较混凝土腹板的横向抗弯刚度小,波形钢腹板箱梁腹板对顶板的约束接近简支而混凝土腹板箱梁的腹板对顶板的约束接近固结,使波形钢腹板箱梁桥的桥面板最大横向弯矩远高于同类混凝土腹板箱梁的弯矩,在设计中需区别对待。
3) 类似规范中混凝土箱梁桥面板横向设计弯矩的计算公式,给出单箱波形钢腹板箱梁桥桥面板横向力简化计算建议公式:将与计算跨径相同的简支板跨中弯矩的90%作为桥面板跨中设计弯矩,将简支板跨中弯矩的70%作为支点处的设计弯矩。
参考文献:
[1] 徐强, 万水. 波形钢腹板PC组合箱梁桥设计与应用[M]. 北京: 人民交通出版社, 2009: 1-11.
XU Qiang, WAN Shui. Design and application of PC box-girder with corrugated steel webs[M]. Beijing: China Communications Press, 2009: 1-11.
[2] JIANG R J, KWONG A F T, XIAO Y F. Prestressed concrete girder bridges with corrugated steel webs: review[J]. Journal of Structural Engineering, 2015, 141(2): 1-9.
[3] HE Jun, LIU Yuqing, CHEN Airong, et al. Bending behavior of concrete-encased composite I-girder with corrugated steel web[J]. Thin-Walled Structures, 2014, 74(9): 70-84.
[4] LHO S H, LEE C H, OH J T, et al. Flexural capacity of plate girders with very slender corrugated webs[J]. International Journal of Steel Structures, 2014, 14(4): 731-744.
[5] 杨丙文, 黎雅乐, 万水, 等. 波形钢腹板箱梁的扭转应力分析[J]. 华南理工大学学报(自然科学版), 2012, 40(2): 19-23.
YANG Bingwen, LI Yale, WAN Shui, et al. Stress analysis of box girders with corrugated steel webs under torsion[J]. Journal of South China University of Technology (Natural Science), 2012, 40(2): 19-23.
[6] KO H J, MOON J, SHIN Y W, et al. Non-linear analyses model for composite box-girders with corrugated steel webs under torsion[J]. Steel and Composite Structures, 2013, 14(5): 409-429.
[7] DING Yong, JIANG Kebin, SHAO Fei, et al. Experimental study on ultimate torsional strength of PC composite box-girder with corrugated steel webs under pure torsion[J]. Structural Engineering and Mechanics, 2013, 46(4): 519-531.
[8] NIE Jianguo, ZHU Li, TAO Muxuan, et al. Shear strength of trapezoidal corrugated steel webs[J]. Journal of Constructional Steel Research, 2013, 85(6): 105-115.
[9] BARAKAT S, MANSOURI A A, ALTOUBAT S. Shear strength of steel beams with trapezoidal corrugated webs using regression analysis[J]. Steel and Composite Structures, 2015, 18(3): 757-773.
[10] LEE D H, OH J Y, KANG H, et al. Structural performance of prestressed composite girders with corrugated steel plate webs[J]. Journal of Constructional Steel Research, 2015, 104: 9-21.
[11] ELDIB M E A H. Shear buckling strength and design of curved corrugated steel webs for bridges[J]. Journal of Constructional Steel Research, 2009, 65(12): 2129-2139.
[12] GUO T, SAUSE R. Analysis of local elastic shear buckling of trapezoidal corrugated steel webs[J]. Journal of Constructional Steel Research, 2014, 102(11): 59-71.
[13] 杨丙文, 黎雅乐, 万水, 等. 波形钢腹板箱梁畸变应力分析[J]. 东南大学学报(自然科学版), 2011, 41(5): 1065-1069.
YANG Bingwen, LI Yale, WAN Shui, et al. Stress analysis of box girders with corrugated steel webs under distorsion[J]. Journal of Southeast University (Natural Science), 2011, 41(5): 1065-1069.
[14] 马磊, 万水, 蒋正文, 等. 单箱多室波形钢腹板箱梁荷载横向分布[J]. 东南大学学报(自然科学版), 2014, 44(1): 145-149.
MA Lei, WAN Shui, JIANG Zhengwen, et al. Load transverse distribution of single box multi-cell girder with corrugated steel webs[J]. Journal of Southeast University (Natural Science), 2014, 44(1): 145-149.
[15] 张华南, 韩昀, 万水. 多室波形钢腹板PC组合箱梁横向受力研究[J]. 重庆交通大学学报(自然科学版), 2009, 28(4): 652-657.
ZHANG Huanan, HAN Yun, WAN Shui. Mechanic characteristics of multi-cell box girder with corrugated steel webs[J]. Journal of Chongqing Jiaotong University (Natural science), 2009, 28(4): 652-657.
[16] 彭鲲, 李立峰, 王文. 波形钢腹板组合箱梁的顶板横向受力有效分布宽度试验研究[J]. 中外公路, 2009, 29(5): 164-167.
PENG Kun, LI Lifeng, WANG Wen. Experimental study on lateral effective width of box girder with corrugated steel webs[J]. Journal of China & Foreign Highway, 2009, 29(5): 164-167.
[17] 刘清. 波形钢腹板组合箱梁横向内力理论及试验研究[D]. 长沙: 湖南大学土木工程学院, 2009: 55-60.
LIU Qing. Theoretical and experimental study on the transverse internal force of the composite box girder with corrugated steel webs[D]. Changsha: Hunan University. Department of Civil Engineering, 2009: 55-60.
[18] JTG D62—2004, 公路钢筋混凝土及预应力混凝土桥梁设计规范[S].
JTG D62—2004, Code for design of highway reinforced concrete and prestressed concrete bridges and culverts[S].
[19] 黄浩, 杨丙文, 万水. 波形钢腹板箱梁横向设计分析[C]// 第20届全国结构工程学术会议论文集(第二册). 北京:《工程力学》杂志社, 2011: 149-154.
HUANG Hao, YANG Bingwen, WAN Shui. Analysis on transverse design of box-girder with corrugated steel webs[C]// Proceedings(volume Ⅱ) of 20th National Conference on Structural Engineering. Beijing: Engineering Mechanics Press, 2011: 149-154.
[20] KRISTEK V. Theory of box girders[M]. New York: John Wiley and Sons Ltd, 1979: 15-20.
[21] 王新敏. ANSYS结构分析单元与应用[M]. 北京: 人民交通出版社, 2011: 187-190.
WANG Xinmin. Analysis and application of structure with ANSYS Software[M]. Beijing: China Communications Press, 2011:187-190.
[22] 刘岚, 崔铁万. 本谷桥的设计与施工: 采用悬臂架设施工法的波纹形钢腹板预应力混凝土箱梁桥[J]. 国外桥梁, 1999(3): 18-25.
LIU Lan, CUI Tiewan. Construction and design of Bengu bridge: cantilever erection application on box-girder with corrugated steel webs[J]. World Bridges, 1999(3): 18-25.
(编辑 刘锦伟)
收稿日期:2015-08-18;修回日期:2015-10-17
基金项目(Foundation item):国家自然科学基金资助项目(51478107);江苏省高校自然科学研究面上项目(15KJD580001)(Project(51478107) supported by the National Natural Science Foundation of China; Project(15KJD580001) supported by the University Natural Science Research Project of Jiangsu Province)
通信作者:黎雅乐,讲师,从事组合结构桥梁、桥梁动力分析等研究;E-mail:liyale@seu.edu.cn