DOI: 10.11817/j.issn.1672-7207.2019.05.003

移动式打磨作业粉尘分布规律及其影响因素

蒋仲安，高康宁，陈记合，兰桂

(北京科技大学 土木与资源工程学院，北京，100083)

摘要：为了探究移动式打磨作业粉尘扩散分布规律及其影响因素，根据气溶胶力学和流体力学原理，在高斯扩散模型基础上建立移动式打磨作业粉尘扩散分布数学模型；利用Python语言设计基于该模型的数据可视化仿真程序，并通过该仿真程序探究粉尘源强、平均粒径、风速及稳定度这4个因素对粉尘质量浓度分布的影响。研究结果表明：在打磨作业阶段，粉尘集中分布在打磨作业点处，粉尘云的位置和质量浓度呈稳定状态；打磨作业结束后，粉尘质量浓度随时间延长而逐渐降低，粉尘云向下游漂移且向四周扩散，其影响半径增大；粉尘质量浓度随源强增强而增大，源强对粉尘质量浓度峰值的位置无影响；粉尘平均粒径越小，粉尘质量浓度越高；风速越大，粉尘质量浓度整体越低，粉尘质量浓度峰值的位置越靠近打磨作业点；当大气稳定度在A~D范围内时，大气稳定度越高，粉尘质量浓度越高，粉尘质量浓度峰值位置有向打磨作业点下风侧移动的趋势；当大气稳定度为F时，粉尘的迁移距离最远。

关键词：打磨；数学模型；粉尘质量浓度；影响因素；分布规律

中图分类号：X502; X964             文献标志码：A         文章编号：1672-7207(2019)05-1028-07

Dust distribution rule and influencing factors in mobile grinding operation

JIANG Zhongan, GAO Kangning, CHEN Jihe, LAN Gui

(School of Civil and Resource Engineering, University of Science and Technology Beijing, Beijing 100083, China)

Abstract: In order to investigate the distribution and influencing factors of dust diffusion in mobile grinding operations, a dust diffusion model for grinding operations was established based on aerosol mechanics, fluid dynamics theory and Gaussian diffusion model. A simulation program based on the model was implemented in Python. Through the simulation program, the effects of dust source intensity, average diameter, wind speed and stability on distribution of dust mass concentration were investigated. The results show that during the grinding operation, dust is concentrated at the grinding operation point, and the position and mass concentration of dust clouds are stable. After the grinding operation, the dust mass concentration gradually decreases with time, and the dust cloud drifts downstream and goes around. The influenced area of dust cloud is thus enlarged. The dust mass concentration increases with the increase of source intensity, and the magnitude of the source intensity has no influence on the position of the dust mass concentration peak. The dust mass concentration increases with the decrease of the average diameter. The dust mass concentration decreases and the position of the dust mass concentration peak is closer to the grinding operation point as the wind speed increases. In the range of atmospheric stability A to D, the dust mass concentration increases and the peak position of the dust mass concentration moves toward the downwind side of the grinding operation point with the increase of atmospheric stability. The dust migration distance is the longest when the atmospheric stability is F.

Key words: grinding; mathematical model; dust mass concentration; influence factors; distribution law

打磨工艺是金属制品机械加工的重要工序，打磨使用的砂轮主要由刚玉和金刚石制成，主要成分为Al₂O₃和SiC，此外还有树脂和二氧化硅。打磨作业过程中产生的粉尘含有大量游离型二氧化硅和金属颗粒物，长期吸入易使人患尘肺病和金属粉尘沉着症。此外，打磨产生的金属粉尘具有爆炸危险性，给安全生产带来极大隐患^[1]。工作人员在打磨大型型材时位置并不固定，作业过程中产生粉尘的地点不固定、时间不连续的特点决定了尘源具有移动性和阵发性。对于除尘技术而言，由于型材尺寸的限制无法使用吸尘打磨台，而采用固定式密闭罩、顶吸罩等粉尘捕集技术效果并不理想。目前，对于粉尘的研究，常用的方法有理论分析研究、计算流体力学(CFD)数值仿真和相似模型实验。在理论分析方面，蒋仲安等^[2]提出采用梯度下降法求解双尘源耦合下呼吸性粉尘扩散的紊流系数。在实验方面，陈举师等^[3]根据相似准则设计了破碎硐室、胶带输送巷道等作业场所的模型，进行了相似实验。在CFD数值仿真方面，孙大伟^[4]利用CFD软件研究了木工镂铣作业粉尘分布规律。本文作者通过对打磨粉尘分布进行理论分析和数值仿真，探索影响打磨粉尘分布的影响因素，以期为有效控制打磨作业产生的大量粉尘、研发便携式除尘技术与装备提供参考。

1  移动式打磨作业粉尘分布模型

由于打磨作业过程中产生的粉尘具有移动性和阵发性，因此，可将该粉尘扩散过程视为非正常排放。根据非正常排放模型^[5-6]，尘源下风侧粉尘质量浓度ρ_a表达式为

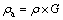               (1)

式中：ρ为连续排放模式下粉尘质量浓度；G为非正常排放项系数。

1.1  连续排放模式下粉尘质量浓度计算公式

移动式打磨作业粉尘扩散坐标系如图1所示。根据高斯扩散模型^[7-11]，对于连续排放源，尘源点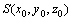下风侧任一点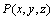的污染物质量浓度ρ为

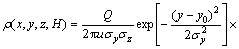
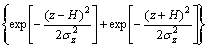     (2)

式中：Q为源强，即单位时间内的产尘量，mg/s；σ_y和σ_z分别为y和z方向的扩散系数；u为风速，取为x轴正方向，m/s；H为有效高度，m。

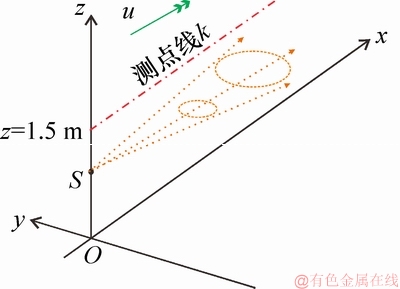
图1  移动式打磨作业粉尘扩散坐标系

Fig. 1  Dust diffusion coordinate system of mobile grinding operation

由于打磨作业产生的粉尘扩散过程中存在明显的重力沉降^[12]，而高斯模型采用镜像法，假设地面像镜面一样，对污染物起反射作用，将这部分的质量浓度贡献视为虚源的作用，因此，不能考虑高斯扩散模型中虚源的作用，而采用“倾斜烟云模式”中的地面反射系数对其进行修正：

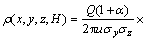
       (3)

式中：α为地面反射系数^[13]。

对于单一粒子在重力作用下的运动，粒子所受到的力有重力F_g、阻力F_f和浮力F_d，其中，浮力等于同体积空气的重量，由牛顿定律可得：

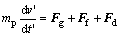            (4)

式中：m_p为粉尘质量，mg；v′为粉尘运动速度，m/s；t'为粉尘运动时间。对于球形粒子，有

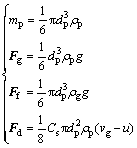
式中：v_g为粉尘最终沉降速度，m/s；g为重力加速度，m/s²；ρ_g为空气密度，kg/m³；ρ_p为粉尘颗粒密度，kg/m³；d_p为粉尘颗粒直径，m；C_s为阻力系数。

粒子雷诺数Re为

              (5)

式中：μ_g为空气的动力黏度，Pa·s。

联立式(4)和(5)，由于粒子达到稳定运动状态时，dRe/dt'=0，则可得出粒子最终沉降速度v_g为

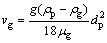             (6)

由于空气密度ρ_g的影响可以忽略不计，所以，

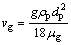               (7)

粉尘粒子离开尘源点后自由沉降距离为v_gt，t为粉尘粒子从尘源点S(x₀, y₀, z₀)扩散到下游预测点P(x, y, z)处的时间，因而粒子的沉降距离为v_g(x-x₀)/u，则有效高度H为

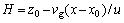           (8)

将式(7)代入式(8)，整理得：

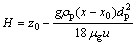           (9)

将式(9)代入式(3)得：

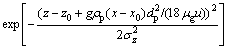  (10)

1.2  非正常排放项系数

打磨作业发生在有限时间t_L内，预测时间点为t。根据非正常排放模型，非正常排放系数G按下式取值：

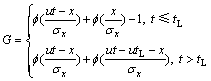     (11)

式中：f为正态分布的概率密度函数；s_x为x方向的扩散系数。

2  数值仿真的实现

Python是一门解释型、可移植、面向对象的高级编程语言，近年来在科学计算可视化、大数据分析与处理、深度学习等科学领域有着广泛的应用。随着NumPy，SymPy和Matplotlib等第三方库的开发，Python越来越适合进行科学计算以及绘制高质量的2D和3D图像，因此，非常适合各个领域的科研人员使用。

在现有的粉尘扩散仿真研究中，一般选用Fluent和EDEM等商用CFD软件，通过内置的DPM，DDMP和DEM等通用的模型进行仿真计算^[14-16]，基于特定数学模型的仿真较少。对于研究移动打磨作业粉尘分布规律这一问题，本文依据第1节推导的数学模型，编写了基于Python语言的更有针对性的仿真程序^[17-19]，该仿真程序主要包括仿真参数设置、图像显示、图像操作与设置等模块。根据各部分的功能将该仿真程序划分为界面层、核心层和支持层3部分，仿真程序设计结构如图2所示。

1) 界面层。本层为用户界面，具有仿真参数输入、计算结果的输出和保存，以及仿真结果的可视化输出等交互功能。

2) 核心层。由自定义模型组成，包括移动打磨作业粉尘扩散数学模型和数据可视化模型，通过调用本层2个模型内的函数和支持层提供的应用程序接口(API)实现对用户输入参数的仿真计算和输出展示功能。

图2  仿真程序设计结构

Fig. 2  Structure of simulation program design

3) 支持层。由Python标准库、开源模块以及更底层的计算机硬件和操作系统组成，各模块具体功能如下。

a) Numpy可以快速、高效地创建多维数组对象，并且对其执行元素级计算和数学运算，为Python提供快速的数组处理能力，同时也是算法之间传递数据的容器。本文利用Numpy作为矩阵的容器将数据在数学模型和绘图模型间传递和运算。

b) Matplotlib是用于绘制数据图表的Python库，提供了非常友好的交互式数据绘图环境。本文以Matplotlib为基础，建立数据可视化的绘图模型，用以绘制粉尘分布曲线图、二维等高线图和三维等高线图。

c) Scipy是一组专门解决科学计算中各种标准问题域的包的集合。本文使用scipy.state包中的相关函数，对粉尘扩散模型进行求解计算。

d) Tkinter是Python内置的标准面向对象接口Tk GUI API，使Python程序可以生成可移植的本地观感的GUI，本文利用Tkinter库设计制作用户交互界面。

仿真的基本过程如下：先根据输入的边界条件生成网格采样点，然后根据粉尘分布数学模型计算网格采样点处的粉尘质量浓度，再通过数据可视化模型将计算结果绘制成图像展现出来。

3  仿真分析

为了研究不同时间段内粉尘的分布情况，模拟源强为300 mg/s，粉尘平均粒径为25 μm，粉尘密度为2 500 kg/m³，风速为2 m/s，大气稳定度为A，打磨时间t_m为300 s，尘源位置为S(0，0，0.8) m的情况下，不同时间下呼吸带平面(z=1.5 m)上粉尘质量浓度分布情况如图3所示。

由图3可知：在打磨工作进行阶段即0~300 s内，粉尘集中在打磨作业点处，最高质量浓度达12 mg/m³，粉尘云位置和质量浓度呈稳定状态；在300 s以后，由于停止了打磨作业，尘源停止了排放，在风流的净化作用和粉尘自身的重力沉降作用下，粉尘质量浓度随时间逐渐降低，同时，粉尘云随风向下游漂移且向四周扩散，影响半径增大。

3.1  源强对粉尘分布的影响

源强为单位时间内污染物的排放量，在本文中为打磨作业在单位时间内的产尘量。在源强分别为100，150，200，250和300 mg/s，粉尘平均粒径为25 μm，粉尘密度为2 500 kg/m³，风速为2 m/s，大气稳定度为A的情况下，在250 s时测点线k上粉尘的质量浓度分布如图4所示。

由图4可知：当源强为100~300 mg/s时，打磨作业产生的源强越强，粉尘质量浓度整体越高；当源强达到300 mg/s时，粉尘最高质量浓度大于12 mg/m³，而当源强为100 mg/s时，最高粉尘质量浓度只有4 mg/m³；源强对粉尘质量浓度峰值的位置并无影响；源强越大，单位时间内产尘量越高。因此，治理打磨粉尘应从尘源入手，建议使用便携式防尘辅助装置或可移动的除尘设备。

图3  不同时间粉尘质量浓度分布等值线图

Fig. 3  Dust mass concentration contour in different times

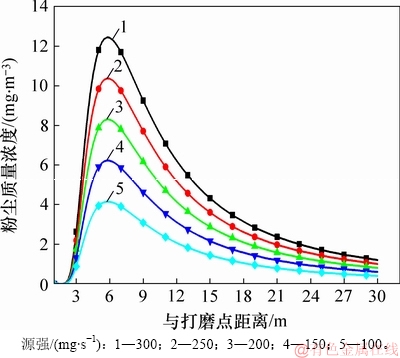
图4  不同源强下粉尘质量浓度的变化

Fig. 4  Change of dust mass concentration with different source intensities

3.2  粉尘平均粒径对粉尘分布的影响

为研究粉尘平均粒径对粉尘扩散分布的影响，分别模拟粉尘平均粒径为10，25，35和65 μm，粉尘源强为300 mg/s，风速为2 m/s，大气稳定度为A，时间为250 s时测点线k上的粉尘分布，如图5所示。

由图5可知：粉尘质量浓度随着粉尘平均粒径的增大而减小，当粉尘平均粒径为10 μm时，粉尘质量浓度峰值达18 mg/m³；当粉尘平均粒径65 μm时，粉尘质量浓度峰值只有1 mg/m³。这是因为粉尘平均粒径越大，重力沉降作用越明显，地面的反射作用也就越弱，粉尘质量浓度也就越低。

图5  不同粉尘平均粒径下粉尘质量浓度的变化

Fig. 5  Change of dust mass concentration with different average diameters of dust

3.3  风速对粉尘分布的影响

为研究风速对粉尘扩散分布的影响，分别模拟风速为1.0，1.5，2.0，2.5，3.0 m/s，粉尘源强为300 mg/s，粉尘平均粒径为25 μm，粉尘密度为2 500 kg/m³，大气稳定度为A的情况下，在250 s时测点线k上的粉尘质量浓度分布，如图6所示。

由图6可知：风速在1~3 m/s范围内，风速越大，在呼吸带高度粉尘质量浓度越低；当风速为3 m/s时，粉尘最高质量浓度只有9.0 mg/m³，而当风速为1 m/s时，粉尘最高质量浓度达到17.5 mg/m³；随着风速增大，粉尘质量浓度峰值的位置越靠近打磨作业产尘点。仿真结果表明风速越大对粉尘的净化效果越好，但根据生产现场实际情况，当风速较大时，会将已经沉降到地面的积尘扬起，造成二次扬尘。因此，经综合考虑，选取的最佳风速应小于扬尘风速。

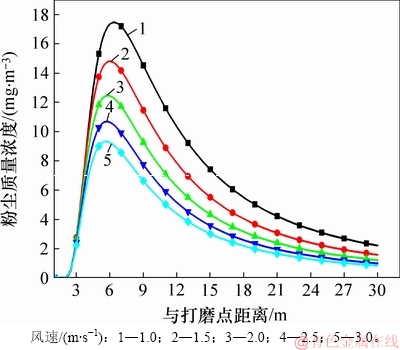
图6  不同风速下粉尘质量浓度的变化

Fig. 6  Change of dust mass concentration with different wind velocities

3. 4  大气稳定度对粉尘分布的影响

大气稳定度是表征大气状态或运动特性的参数，影响到空气对粉尘的扩散稀释能力。对大气稳定度的定义和分类方法很多，较常用的是帕斯奎尔稳定度分级法^[20]，该方法将大气稳定度从低到高划分为A，B，C，D，E和F这6个等级。为了研究稳定度对粉尘质量浓度分布的影响，分别在源强为300 mg/s，粉尘平均粒径25 μm，粉尘密度为2 500 kg/m³，风速为2 m/s的情况下，在250 s时不同大气稳定度下测点线k上的粉尘分布，模拟结果如图7所示。

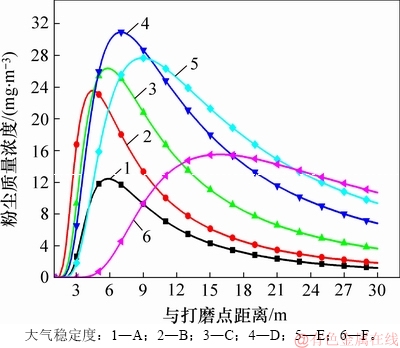
图7  不同稳定度下粉尘质量浓度的变化

Fig. 7  Dust mass concentration variations in different atmospheric stabilities

由图7可知：在大气稳定度A~D范围内，稳定度越高，粉尘质量浓度整体越高，这是因为稳定度越高，对应的扩散参数就越低，风流对粉尘的净化能力也就越低；当大气稳定度为D时，粉尘质量浓度峰值最高，达到30 mg/m³；当大气稳定度为A时，粉尘质量浓度峰值最低，为12 mg/m³；随着大气稳定度增高，粉尘质量浓度值整体有远离z轴的趋势(向下风侧移动的趋势)；大气稳定度在A~E范围内，粉尘质量浓度在短距离内迅速增大至最大值，之后迅速衰减；而当大气稳定度为F时，粉尘质量浓度缓慢增大，因此，达到质量浓度峰值的距离较长；当粉尘质量浓度到达最大值后衰减速率同样较小，因此，粉尘的迁移距离较远，影响区域较大。

4 结论

1) 在高斯扩散模型的基础上，建立移动式打磨作业粉尘分布模型；基于该模型，利用Python语言设计编写仿真程序，探究了粉尘源强、平均粒径、风速、稳定度4个影响因素对粉尘分布的影响效应。

2) 在打磨作业阶段，粉尘云的位置和质量浓度呈稳定状态；打磨作业结束后，粉尘质量浓度随时间逐渐降低，粉尘云随风向下游漂移且向四周扩散；粉尘平均粒径越小，粉尘质量浓度越高；在大气稳定度A~D范围内，大气稳定度越高，粉尘质量浓度越高，粉尘质量浓度峰值位置有向下风侧移动的趋势。大气稳定度为F时粉尘的迁移距离最远。

3) 源强越强，粉尘质量浓度越高，但源强对粉尘质量浓度峰值位置无影响。治理打磨粉尘应从尘源入手，在生产中，建议采用手持打磨工具便携防尘辅助装置或可移动的便携式除尘设备。风速越大，粉尘质量浓度越低，粉尘质量浓度峰值位置越靠近打磨作业点；当风速过大时，考虑到二次扬尘作用，最佳风速应小于扬尘风速。

参考文献：

[1] 多英全, 刘垚楠, 胡馨升. 2009—2013 年我国粉尘爆炸事故统计分析研究[J]. 中国安全生产科学技术, 2015, 11(2): 186-190.

DUO Yingquan, LIU Yaonan, HU Xinsheng. Statistical analysis on dust explosion accidents occurring in China during 2009—2013 [J]. Journal of Safety Science and Technology, 2015, 11(2): 186-190.

[2] 蒋仲安, 陈雅, 王佩. 双尘源耦合下呼吸性粉尘扩散的紊流系数求解[J]. 哈尔滨工业大学学报, 2017, 49(8): 129-134.

JIANG Zhongan, CHEN Ya, WANG Pei. Solution of turbulence coefficient in the diffusion of respirable dust under the coupling of two dust sources[J]. Journal of Harbin Institute of Technology, 2017, 49(8): 129-134.

[3] 陈举师, 蒋仲安, 张义坤. 破碎硐室粉尘质量浓度分布规律的实验研究[J]. 东北大学学报(自然科学版), 2015, 36(7): 1051-1055.

CHEN Jushi, JIANG Zhongan, ZHANG Yikun. Experimental study on dust concentration distribution in crushing chamber [J]. Journal of Northeastern University(Natural Science), 2015, 36(7): 1051-1055.

[4] 孙大伟. 木工镂铣作业粉尘分布规律研究[D]. 哈尔滨: 哈尔滨理工大学测控技术与通信工程学院, 2017: 5-6.

SUN Dawei. Study on the distribution in woodworking router operation [D]. Harbin: School of Measurement-Control Technology and Communications Engineering. Harbin University of Science and Technology, 2017: 5-6.

[5] 罗艾民, 魏利军. 有毒重气泄漏安全距离数值方法[J]. 中国安全科学学报, 2005, 15(8): 98-100.

LUO Aimin, WEI Lijun. Numerical method of safety distance for poisonous dense gaseous leakage[J]. China Safety Science Journal, 2005, 15(8): 98-100.

[6] 邓文英, 丁训静. 净水厂氯气泄漏的环境风险分析[J]. 环境监测管理与技术, 2008, 20(4): 54-56.

DENG Wenying, DING Xunjing. Analysis on environmental risk of liquid chlorine leakage in water plant[J]. The Administration and Technique of Environmental Monitoring, 2008, 20(4): 54-56.

[7] 何宁, 吴宗之, 郑伟. 一种改进的有毒气体扩散高斯模型算法及仿真[J]. 应用基础与工程科学学报, 2010, 18(4): 571-580.

HE Ning, WU Zongzhi, ZHENG Wei. Simulation of an improved gaussian model for hazardous gas diffusion[J]. Journal of Basic Science and Engineering, 2010, 18(4): 571-580.

[8] ARYSTANBEKOVA N K. Application of Gaussian plume models for air pollution simulation at instantaneous emissions[J]. Mathematics and Computers in Simulation, 2004, 67(4/5): 451-458.

[9] WEIL J C, BROWER R P. An updated Gaussian plume model for tall stacks[J]. Journal of the Air Pollution Control Association, 1984, 34(8): 818-827

[10] BRUSCA S, FAMOSO F, LANZAFAME R, et al. Theoretical and experimental study of Gaussian plume model in small scale system[J]. Energy Procedia, 2016, 101: 58-65.

[11] 闪顺章, 王从陆. 焊接烟尘扩散数学模型研究[J]. 中国安全生产科学技术, 2018, 14(6): 117-181.

SHAN Shunzhang, WANG Conglu. Study on numerical model for diffusion of welding fume[J]. Journal of Safety Science and Technology, 2018, 14(6): 117-181.

[12] 樊建人, 姚军, 张新育, 等. 气固两相流中颗粒—颗粒随机碰撞新模型[J]. 工程热物理学报, 2001, 22(5): 629-632.

FAN Jianren, YAO Jun, ZHANG Xinyu, et al. Modeling particle-to-particle interactions in gas-solid flows[J]. Journal of Engineering Thermophysics, 2001, 22(5): 629-632.

[13] 郭廷忠. 环境影响评价学[M].北京: 科学出版社, 2007: 110-111

GUO Tingzhong. Environmental impact assessment[M]. Beijing: Science Press,2007: 110-111

[14] SHI Guoqing, LIU Maoxi, GUO Zhixiong, et al. Unsteady simulation for optimal arrangement of dedusting airduct in coal mine heading face[J]. Journal of Loss Prevention in the Process Industries, 2017, 46: 45-53.

[15] ZHOU Gang, ZHANG Qi, BAI Ruonan, et al. The diffusion behavior law of respirable dust at fully mechanized caving face in coal mine: CFD numerical simulation and engineering application[J]. Process Safety and Environmental Protection, 2017, 106: 117-128.

[16] HU Shengxong, FENG Guorui, REN Xiangyan, et al. Numerical study of gas–solid two-phase flow in a coal roadway after blasting[J]. Advanced Powder Technology, 2016, 27(4): 1607-1617.

[17] 李明, 吴超. 粉尘点污染扩散模型的可视化研究[J]. 环境科学与技术, 2006, 29(11): 12-14.

LI Ming, WU Chao. Visualization for dust source diffusion models[J]. Environmental Science And Technology, 2006, 29(11): 12-14+115-116.

[18] 刘振平, 贺怀建, 李强, 等. 基于 Python 的三维建模可视化系统的研究[J]. 岩土力学, 2009, 30(10): 3037-3042.

LIU Zhenping, HE Huaijian, LI Qiang, et al. Study of the technology of 3D modeling and visualization system based on Python[J]. Rock and Soil Mechanics, 2009, 30(10): 3037-3042.

[19] 徐丙立, 林珲, 胡亚, 等. 多点源空气污染高斯扩散模式并行方法研究[J]. 北京理工大学学报, 2014, 34(11): 1145-1149.

XU Bingli, LIN Hui, HU Ya, et al. Design and implement a parallel algorithm of Gauss plume model for air pollution dispersion[J]. Transactions of Beijing Institute of Technology, 2014, 34(11): 1145-1149.

[20] 李小忠, 侯祺棕, 高燕, 等. 城市大气稳定度分级模型的研究[J]. 工业安全与防尘, 2001, 27(4): 27-31.

LI Xiaozhong, HOU Qizong, GAO Yan, et al. Study on model of classification of urban air stabilization[J]. Industrial Safety and Environmental Protection, 2001, 27(4): 27-31.

(编辑  伍锦花)

收稿日期：2018-06-24；修回日期：2018-08-24

基金项目(Foundation item)：国家重点研发计划项目(2016YFC0801700)(Project (2016YFC0801700) supported by the National Key Research and Development Program of China)

通信作者：蒋仲安，教授，博士生导师，从事矿井通风安全及粉尘控制研究；E-mail: jza1963@263.com