DOI: 10.11817/j.issn.1672-7207.2015.01.022

基于光电测量平台的多目标定位算法

徐诚¹，黄大庆^{1, 2}

(1. 南京航空航天大学 电子信息工程学院，江苏 南京，210016；

2. 南京航空航天大学 无人机研究院，江苏 南京，210016)

摘要：为了提高空中对地面目标定位的效率，达到1次测量、多点定位的目的，提出一种基于光电测量平台的多目标定位方法。首先，建立大地坐标系、地理坐标系、载机坐标系、摄像机坐标系等7个坐标系及坐标系之间的转换关系。然后，根据目标定位过程中测量点、目标点、成像点的几何位置，结合载机姿态角、摄像机姿态角、激光测距、摄像机焦距等参数，推导出拍摄图像中任意像素点在摄像机坐标系中的坐标，并通过坐标变换进一步计算出目标点的经纬度、高度，从而实现多目标定位。利用光电测量平台对地面目标进行定位实验。研究结果表明：与传统的单目标定位相比，多目标定位不仅提高定位效率，而且能满足一定的定位的精度要求，具有较大的实用和推广价值。

关键词：光电测量；多目标；目标定位；定位效率

中图分类号：TH74             文献标志码：A         文章编号：1672-7207(2015)01-0157-07

Multiple-target localization based on electro-optical measurement platform

XU Cheng¹, HUANG Daqing^{1, 2}

(1. College of Electronic and Information Engineering, Nanjing University of Aeronautics & Astronautics,

Nanjing 210016, China;

2. Research Institute of UAV, Nanjing University of Aeronautics & Astronautics, Nanjing 210016, China)

Abstract: In order to improve the efficiency of air to ground target localization and achieve the effect of a time measurement and multi-point positioning, a multi-target localization algorithm on electro-optical measurement platform was proposed. First, 7 coordinate system such as geodetic coordinate system, geographic coordinate system, UAV body coordinate system and camera coordinate system, including the transfer relationship between them were established. Then based on the geometric position of measuring point, target point and image point, combining several parameters such as UAV attitude angle, camera attitude angle, laser range value and camera focal length, the position of any image point in camera coordinate system was deduced. And through coordinate transformation, the longitude, latitude and height of target point in the image can be calculated. Tested by experiments, multi-target localization can not only improve the efficiency, but also satisfy certain precision compared with the traditional single target localization, which has great practical and popularization value.

Key words: electro-optical measurement; multi-target; target localization; positioning efficiency

航空测量是一种快速、有效的测量手段，空中对地面目标的定位在救灾预警、精确制导、GIS数据更新等应用领域有十分重要的意义。长期以来，空中对地面目标定位受到研究人员的密切关注^[1-2]。国内外一些学者从不同的应用侧面对目标定位的方法进行了分析和讨论。Redding等^[3]给出了一种从小型固定翼飞机获取的图像中定位地面目标方法，应用目标在图像中的像素位置，结合飞机的位置和高度、相机姿态角，实现目标定位；淡金强等^[4]提出了在DEM的基础上，以摄像机为“视点”，通过透视模型的变换与相关算法计算获取所摄对像三维坐标的单摄像机测量定位方法；余家祥等^[5]提出的空中对地定位方法，通过线性化共线条件方程建立摄像机姿态角和焦距迭代计算模型, 根据非共线位置拍摄的多帧图像及其至少3个可识别同名像点坐标迭代计算摄像机姿态角和焦距的精确值，然后利用多摄站前方交会法求取地面目标的三维坐标；雷仲魁等^[6]提出一种新的逆速高比补偿测高法来获得相对高度数据，用于无激光测距仪的小型无人机光电侦察平台目标定位实时解算，具有测量速度快，同时不额外增加硬件设备的优点。毛昭军等^[7]提出一种基于姿态测量/ 激光测距的目标定位模型，将载机信息( 位置、姿态)以及光电测量平台信息(云台角度、测距值)，解算出目标的位置信息(经度、纬度、高度)。在以上研究中，姿态测量/激光测距模型目标定位精度最高，在实际工程上已有应用。本文作者在姿态测量/激光测距的目标定位模型基础上，结合目标定位过程中测量点、目标点、成像点的几何位置，提出一种基于光电测量平台的多目标定位方法，对地面某个目标进行1次测距，便可通过算法解算出该目标周围光电视场内多个地面目标的地理位置，极大地提高了测量效率，具有一定的实用价值。

1  系统总体结构

空中对地目标定位的目的是求取目标的三维坐标。本文讨论的飞机装备GPS/INS导航设备和机载光电测量平台。机载光电测量平台以跟踪架为主框架，包含有竖轴、横轴、照准架、摄像机、激光测距机等基本组成部分，主要采用吊舱式及转塔式结构是安放在飞机上^[8-10]。目标定位过程如图1所示。机载光电测量平台需要实时获取飞机的航空姿态测量数据及飞机GPS接收机信息，将这些信息与机载光电测量平台自身的光轴位置及激光测距值相结合，通过坐标变换实现目标定位^[11]。

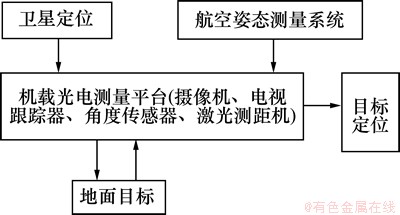
图1  目标定位系统结构

Fig. 1  Target localization system structure

2  多目标定位模型

根据定位机制的不同，将目标点分为2类。其中，位于光电测量平台摄像机视场中心的目标点为主目标点，在实际定位中，需要对其进行激光测距；位于主目标点周围光电视场的目标点为次目标点，对次目标点不进行激光测距。下面将分别讨论主、次目标点的定位方法。

2.1  主目标点定位

首先，定义如下坐标系。

1) 大地坐标系^[12]。大地坐标系原点在地球质心，Z轴指向地球北极，X轴由原点指向格林尼治平子午面与地球赤道交点，Y轴垂直于XOZ平面并与Z轴和X轴构成右手坐标系。在大地坐标系中任一点的坐标以纬度、经度和大地高表示，如图2所示。

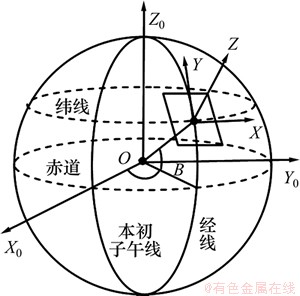
图2  大地坐标系与地理坐标系

Fig. 2  Geodetic coordinate system and geographic coordinate system

2) 空间直角坐标系。空间直角坐标系与大地坐标系重合。在空间直角坐标系中任一点的坐标以直角坐标表示。

3) 地理坐标系。原点是某一时刻载机所处的位置，Y是正北方向，Z指向天顶，Y与Z和X构成右手坐标系，如图2所示。

4) 载机坐标系。原点与地理坐标系的原点重合，当载机坐标系相对地理坐标系的三轴姿态角为0°时，其三轴指向与地理坐标系三轴指向重合。

5) 摄像机坐标系。原点在摄像机光轴与横轴的交点上，Z轴为摄像机光轴，当摄像机在初始位置时，Y轴指向载机机头，Z轴指向机体正下方，X轴与Y轴、Z轴构成右手坐标系。

目标在大地坐标系下的三维坐标可以通过一系列的坐标变换，得出摄像机坐标系下的坐标，具体变换过程如图3所示^[13]。

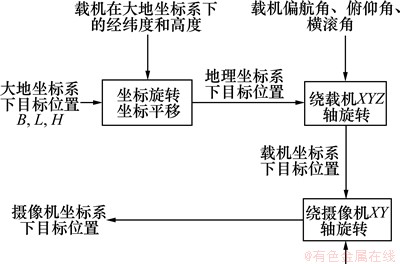
图3  坐标变换框图

Fig. 3  Block diagram of coordinate transformation

1) 大地坐标系下目标位置B(纬度)、L(经度)和H(高度)需要转换为空间直角坐标系下的坐标，然后通过坐标旋转及平移，得到地理坐标系下的目标位置t_g。空间直角坐标系下目标位置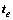由下式可得^[14]：

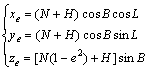            (1)

其中：N为卯酉圈曲率半径，；a为椭球的长半径；e为椭圆的第一偏心率。

地理坐标系下目标位置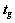由下式可得：

             (2)

其中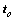：为载机在空间直角坐标系下的坐标。

   (3)

其中：B_o和L_o分别为载机的纬度和经度。

2) 地理坐标系下的目标位置t_g经过坐标旋转，得到载体坐标系下的目标位置t_b。

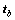
            (4)

其中：；为载机的偏航角；为载机的俯仰角；为横滚角。，和分别为绕X轴、Y轴和Z轴的旋转矩阵。

3) 载体坐标系下的目标位置t_b经过坐标旋转，得到摄像机坐标系下的目标位置t_s。

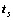
           (5)

其中：；为摄像机旋转的方位角；为摄像机旋转的高低角。

根据式(2)，(4)和(5)可得

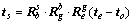           (6)

所以

      (7)

其中：；R为光电测量平台对主目标点的激光测距。

         根据式(7)可以求得主目标点空间直角坐标系下的坐标，采用文献[15]中的算法即可求得目标的经纬度和高度，完成主目标点的定位过程。

2.2  次目标点定位

次目标点定位与主目标点定位相比，缺少光电测量平台到目标点的测距值，即无法直接获取目标点在摄像机坐标系下的坐标t_s。因此，次目标点定位要解决的关键问题为根据目标点在图像中的坐标求得目标点在摄像机坐标系下的坐标。首先，定义如下坐标系。

1) 图像物理坐标系^[16-17]。图像物理坐标系是以光轴与像平面的交点为原点(称为图像主点)，以实际物理尺度(毫米、微米等)为单位的直角坐标系。其中X轴、Y轴分别与图像像素坐标系的X和Y轴平行。

2) 图像像素坐标系。图像像素坐标系是以图像左上角点为原点，以像素为坐标单位的直角坐标系。X和Y分别表示该像素在数字图像中的行数与列数。

依据中心透视投影模型的映射关系(如图4所示)，像点p的图像物理坐标(x_w，y_w)与物点P的摄像机坐标

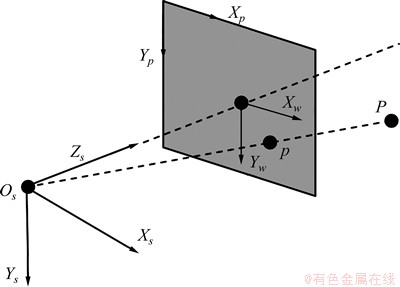
图4  中心透视模型

Fig.4  Central perspective model

系坐标(x_s，y_s，z_s)的关系式为

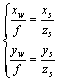                  (8)

其中：f为摄像机的焦距。像点p的图像像素坐标(x_p，y_p)与其图像物理坐标(x_w，y_w)的关系为

              (9)

其中：(C_x，C_y)为图像主点，即光轴与像面交点的图像像素坐标；d_x和d_y分别为摄像机的单个像元在X_w和Y_w方向上的物理尺寸。

目标定位过程中的几何关系见图5。图5中M₁和M₂分别代表成像的场景空间和成像平面。在M₂中，O为摄像机的光轴和像平面的交点，OX和OY分别为像平面的水平和垂直方向上的两轴，P为目标点A在像平面上的投影，D和E分别为P点在像平面内垂直方向和水平方向上的投影。在M₁中，O₂点为摄像机的光轴与地面的交点，O₂X₂为像平面坐标系OX轴在M₁中经过O₂点的投影，O₂Y₂为像平面坐标系OY轴在M₁中的投影，O_s为摄像机镜头中心，O_sO为镜头的焦距f，G为镜头中心O_s在M₁中的投影，O_sX_sY_sZ_s为摄像机坐标系，O_gX_gY_gZ_g为载机的地理坐标系。

O_sA与O_sO₂的夹角ε为

           (10)

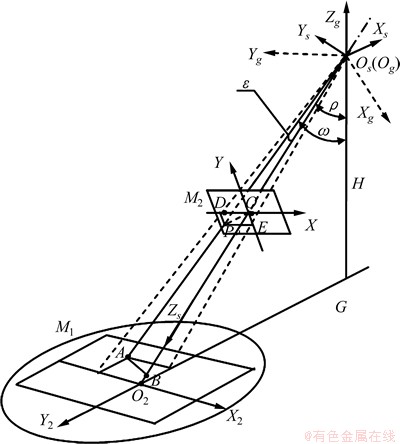
图5  目标定位几何关系图

Fig. 5  Geometric diagram of target localization

ρ为O_sO₂与O_sG的夹角。设为O_sX_sY_sZ_s 中的向量，为O_gX_gY_gZ_g的向量。令t_s在O_gX_gY_gZ_g中的表示为t _sg，有，则

             (11)

ω为O_sA与O_sG夹角。设为O_sX_sY_sZ_s 中的向量，为O_gX_gY_gZ_g的向量。令v_s在O_gX_gY_gZ_g中的表示为v _sg，有，则

            (12)

在图5中，O_sO₂是摄像机镜头中心沿Z_s轴到目标的距离，利用激光测距仪对目标测距，这一距离是已知的。令O_sO₂ = R ，由图5可知：

则A点在O_sX_sY_sZ_s 坐标系中Z轴坐标为

    (13)

将式(10)代入式(13)可得

 (14)

将式(14)代入式(8)可得

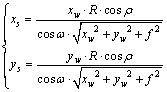           (15)

结合式(15)和式(9)，即可计算出图像中任意一点在摄像机坐标系下的坐标。

至此，根据式(7)即可求得次目标点空间直角坐标系下的坐标。采用文献[15]中的算法即可求得目标的经纬度和高度，完成次目标点的定位过程。

3  实验方案与数据分析

3.1  实验方案

通过具体实验对算法的有效性及定位精度进行验证和评估，实验装置主要包括：1) 光电测量平台和操控系统；2) 三轴转台；3) 数据采集处理系统。实验操作步骤如下。

步骤1 将光电测量平台安装于转台上，机械安装夹具保证安装的稳定性，校正系统，使得摄像机和激光测距机视轴平行。

步骤2 操作摄像机控制手柄，将摄像机的方位和高低角度调节到零位，即为摄像机的初始位置。

步骤3 使用差分卫星定位接收机和航姿参考系统(AHRS)分别测量光电测量平台的纬度B_o、经度L_o，高度H_o以及姿态角，和。

步骤4 操作摄像机控制手柄，同时观察摄像机画面，使得待测量的主目标点位于摄像机视场中心；同时记录摄像机的方位角、高低角以及激光测距。

步骤5 在拍摄图片上均匀选取8个次目标点，如图6所示，其中5号点为主目标，其余点为次目标。记录各次目标点的像素坐标。

3.2  实验数据分析

表1所示为光电测量平台测量数据，表2所示为各目标点在图像中的像素坐标。

编写程序实现多目标定位算法，并将以上测量数据导入程序，计算出1~9号点的经纬度和高度。为了对比验证多目标定位算法的有效性，采用文献[7]中传统单点定位方法对每个目标点进行定位，共进行9次操作，得到9个目标位置数据，并以此为参考值，比较2种定位方法的定位精度，如表3所示。

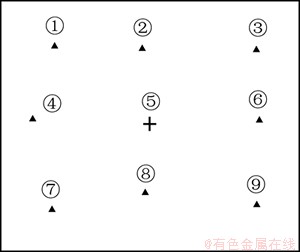
图6  测量点分布图

Fig. 6  Distribution of measuring points

表1  光电测量平台测量数据

Table 1  Measure data of electro-optical measurement platform

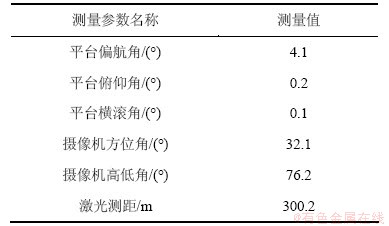
表2  目标点像素坐标

Table 2  Pixel coordinates of target

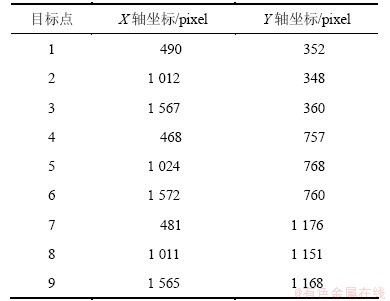
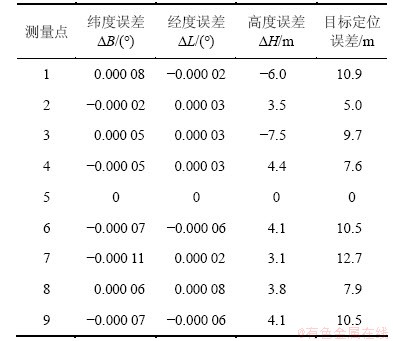
表3中第1列为测量点序号，第2~4列分别为同一测量点使用2种方法定位方法所得数据的纬度差、纬度差和高度差，最后一列为将2~4列差值折算后的空间距离差。由表3可以看出：本次实验中，次目标点的最大定位差值为12.7 m，最小定位差值为5.0 m。主目标的定位精度较高，次目标的定位精度略低于主目标的定位精度。通过多次类似实验，均发现此规律。这是由于多目标定位时，次目标的定位精度与拍摄图片的质量有关。由于镜头设计的复杂性和工艺水平等因素影响，实际成像系统会存在镜头畸变，使光线发生细微的偏移，产生相差^[18]。另外大气抖动、地形起伏、拍摄角度等因素均会带来图像畸变^[19]，导致次目标定位误差加大，最终会使次目标的定位精度低于主目标的定位精度。

表3  目标点定位误差

Table 3  Target localization error

4  结论

1) 提出了一种基于光电测量平台的多目标定位方法。通过建立多个坐标系，在姿态测量/ 激光测距目标定位模型的基础上，结合目标定位过程中测量点、目标点、成像点的几何位置，推导出图像中任意目标点从图像像素坐标系到大地坐标系的映射关系，从而实现了多目标定位。

2) 实验证明了多目标定位算法的有效性。在实验中，次目标点的最大定位差值为12.7 m，最小定位差值为5.0 m。

3) 只需要飞机对地面某个目标进行1次测距，便可通过算法解算出该目标周围光电视场内多个地面目标的地理位置。与以往单目标定位方法相比，该方法能达到一定的精度，同时具有测量效率高的特点，具有一定的实用价值。

参考文献：

[1] 金光. 机载光电跟踪测量的目标定位误差分析和研究[D]. 北京: 中国科学院长春光学精密机械与物理研究所, 2001: 3-6.

JIN Guang. Studying and analyzing on the error of positioning in airborne photo-electricity tracking survey equipment[D]. Beijing: Chinese Academy of Sciences. Changchun Institute of Optics, Fine Mechanics and Physics, 2001: 3-6.

[2] 张小红, 刘经南, Forsberg R. 基于精密单点定位技术的航空测量应用实践[J]. 武汉大学学报(信息科学版), 2006, 31(1): 19-22.

ZHANG Xiaohong, LIU Jingnan, Forsberg R. Application of precise point positioning in airborne survey[J]. Geomatics and Information Science of Wuhan University, 2006, 31(1): 19-22.

[3] Redding J D, McLain T W, Beard R W, et al. Vision-based target localization from a fixed-wing miniature air vehicle[C]// American Control Conference. New York, USA: IEEE, 2006: 6-8.

[4] 淡金强, 马国华, 蒋胜平, 等. 基于DEM的战场目标侦察定位技术研究[J]. 光学技术, 2008, 34(1): 100-104.

DAN Jinqiang, MA Guoping, JIANG shengping, et al. Research on the real-time location of the battlefield target reconnaissance based on the single-vidicon[J]. Optical Technique, 2008, 34(1): 100-104.

[5] 余家祥, 萧德云, 姜鲁东. 基于多帧图像同名点的无人机对地定位新方法[J]. 兵工学报, 2008, 29(3): 300-304.

YU Jiaxiang, XIAO Deyun, JIANG Ludong. A new UAV Geo-location approach based on common points on multiple images[J]. Acta Armamentarii, 2008, 29(3): 300-304.

[6] 雷仲魁, 仲筱艳. 基于逆速高比补偿测高法的侦察目标定位[J]. 遥测遥控, 2010, 31(6): 52-55.

LEI Zhongkui, ZHONG Xiaoyan. Reconnaissance object location with a height measure method based on contra- compensation of velocity to height ratio[J]. Journal of Telemetry, Tracking and Command, 2010, 31(6): 52-55.

[7] 毛昭军, 汪德虎. 姿态测量/激光测距的无人机目标定位模型[J]. 火力与指挥控制, 2003, 28(5): 14-17.

MAO Shaojun, WANG Dehu. A model of target position for UAV based attitude measuring/laser range-finder[J]. Fire Control & Command Control, 2003, 28(5): 14-17.

[8] 耿延洛, 王合龙, 周洪武. 机载光电探测跟踪系统总体精度分析方法研究[J]. 电光与控制, 2004, 11(2): 18-20.

GENG Yanluo, WANG Helong, ZHOU Hongwu. Study on accuracy analysis of airborne electro-optical detecting and tracking system[J]. Electronics Optics & Control, 2004, 11(2): 18-20.

[9] 王平, 王伟, 丁金伟, 等. 机载光电侦察平台复合减振设计[J]. 光学精密工程, 2011, 19(1): 83-89.

WANG Ping, WANG Wei, DING Jinwei, et al. Vibration damping design for airborne electro-optical surveillance platform[J]. Optics and Precision Engineering, 2011, 19(1): 83-89.

[10] 黄亮, 张建强, 刘忠. 空中机动平台光电吊舱对目标定位方法分析[J]. 武汉理工大学学报(交通科学与工程版), 2013, 37(1): 102-105.

HUANG Liang, ZHANG Jianqiang, LIU Zhong. Analysis on target location methods using photoelectric payload of aerial mobile platform[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2013, 37(1): 102-105.

[11] 张葆, 姚俊峰, 高利民. 机载GPS测量定位技术研究[J]. 光学精密工程, 2009, 17(1): 1723-1728.

ZHANG Bao, YAO Junfeng, GAO Liming. Measuring orientation technology based on airborne GPS[J]. Optics and Precision Engineering, 2009, 17(1): 1723-1728.

[12] 王涛, 宋立维. 车载经纬仪的测量误差修正[J]. 仪器仪表学报, 2012, 33(2): 469-473.

WANG Tao, SONG Liwei. Measurement error correction of vehicular theodolite[J]. Chinese Journal of Scientific Instrument, 2012, 33(2): 469-473.

[13] 徐诚, 黄大庆. 无人机光电侦测平台目标定位误差分析[J]. 仪器仪表学报, 2013, 34(10): 2265-2270.

XU Cheng, HUANG Daqing. Error analysis for target localization with unmanned aerial vehicle electro-optical detection platform[J]. Chinese Journal of Scientific Instrument, 2013, 34(10): 2265-2270.

[14] 刘海芳, 王瑞, 钟诗胜, 等. 机载激光对埋地管道的自主定位[J]. 光学精密工程, 2011, 19(8): 12-1254.

LIU Haifang, WANG Rui, ZHONG Shisheng, et al. Helicopter-borne laser autonomous positioning of buried pipeline[J]. Optics and Precision Engineering, 2011, 19(8): 12-1254.

[15] 桑金. 空间大地直角坐标与大地坐标反算的非迭代法[J]. 测绘通报, 2000, 46(5): 37-39.

SANG Jin. Space geodetic rectangular coordinates and geodetic coordinate inverse non-iteration method[J]. Bulletin of Surveying and Mapping, 2000, 46(5): 37-39.

[16] 吴宏明, 周建军, 陈超, 等. 基于平台参数的航空光学图像镶嵌算法研究[J]. 中国图象图形学报, 2011, 16(7): 1248-1254.

WU Hongming, ZHOU Jianjun, CHEN Chao, et al. Algorithm of aerial optical image mosaicing based on platform parameters[J]. Journal of Image and Graphics, 2011, 16(7): 1248-1254.

[17] 王喜权. 微小型无人直升机姿态测量及其在航拍图像校正中的应用设计[D]. 杭州: 浙江大学控制科学与工程学系, 2011: 46-48.

WANG Xiquan. Mini unmanned helicopter attitude measurement and application in aerial image design correction[D]. Hangzhou: Zhejiang University. Department of Control Science and Engineering, 2011: 46-48.

[18] 孙辉, 张淑梅. 机载成像系统像移计算模型与误差分析[J]. 光学精密工程, 2012, 20(11): 2492-2499.

SUN Hui, ZHANG Shumei. Computation model and error budget for image motion of aerial imaging system[J]. Optics and Precision Engineering, 2012, 20(11): 2492-2499.

[19] J A, Corte-Real L. Measures for an objective evaluation of the geometric correction process quality[J]. Geoscience and Remote Sensing Letters, IEEE, 2009, 6(2): 292-296.

(编辑  杨幼平)

收稿日期：2014-02-04；修回日期：2014-04-23

基金项目(Foundation item)：国家自然科学基金资助项目(61106018)；航空科学基金资助项目(20115552031) (Project(61106018) supported by the National Natural Science Foundation of China; Project(20115552031) supported by Aeronautical Science Foundation of China)

通信作者：徐诚，博士研究生，从事光学目标定位研究；E-mail: xc88@vip.qq.com