DOI: 10.11817/j.ysxb.1004.0609.2020-37566

超声振动条件下AZ31B镁合金本构关系

曹秒艳^{1, 2}，田少杰^{1, 2}，胡  晗^{1, 2}，赵长财³，韩旭斌³

(1. 燕山大学 机械工程学院，秦皇岛 066004；

2. 河北省轻质结构装备设计与制备工艺技术创新中心，秦皇岛 066004；

3. 先进锻压成形技术与科学教育部重点实验室(燕山大学)，秦皇岛 066004)

摘  要：通过理论、实验和模拟相结合的方法，探究超声振动在AZ31B镁合金塑性成形中的“体积效应”影响规律及作用机理。首先基于非局部理论建立了超声振动AZ31B镁合金的应力叠加模型并通过模拟进行了验证，然后基于热激活理论和位错演化理论，建立AZ31B镁合金在超声振动条件下的声塑性模型，并结合实验验证了模型的准确性。结果表明：应力叠加效应导致的应力下降值与超声振动振幅参数正相关。引入超声振动产生的应力下降值可以通过应力叠加效应模型和声塑性效应模型刻画。应力叠加效应导致材料的平均流动应力发生振荡而下降；声软化效应指位错吸收超声能量克服钉扎效应，从而利于材料塑性变形；声残余硬化效应主要体现在高超声能量导致材料位错密度大量增殖，位错在晶界处塞积、堆垛形成位错墙，阻碍塑性流动，导致材料出现残余硬化。

关键词：超声振动；应力叠加效应；声塑性效应；本构模型

文章编号：1004-0609(2020)-07-1584-10　　     中图分类号：TG146.2　　     文献标志码：A

铝、镁、钛等轻质合金比强度与比刚度高的特性使其在产品轻量化和资源环境友好化的大趋势下越来越显示出广泛的前景^[1]。但是由于轻合金材料具有塑性低和成形性能差等特点，使得轻合金精确成形制造成为国内外专家学者所面临的一大难题，阻碍着相关行业向前迈进的步伐。例如复杂曲面成形时存在工序复杂、模具开发成本高及尺寸精度低等问题，严重影响零件的质量和可靠性。针对难成形材料的塑性加工问题，国内外专家学者研发出许多新颖、独特的成形技术^[2-3]，其中超声振动辅助成形就是一种较为有效的技术。

超声振动(UV)辅助成形技术是对传统金属塑性成形工艺的一次有效改良。国内外诸多专家学者^[4-6]在拉丝、拉拔、拉深、拉伸、镦粗、挤压等金属塑性变形过程中施加超声振动并对其作用效果进行研究。结果表明相较于传统的金属塑性加工方法，施加超声振动后产品表面质量提高，成形力显著降低。具体主要体现在以下方面：降低了材料的屈服极限，使材料成形载荷降低，塑性和断裂极限提高，改善了材料的力学性能；对高强度、高硬度、脆性大的材料，能有效改善塑性成形性能，降低产品的废品率。

目前在超声振动辅助成形理论研究中关于材料变形抗力降低、材料发生软化现象最为广泛接受的观点就是体积效应(Volume effect)，即超声振动的施加在塑性变形过程中对材料内部本构关系的影响。但已有“体积效应”的机理研究在该领域还不完善，定量理论还缺乏科学严谨的结论。

目前，对于“体积效应”的理论解释主要有两种。一种认为施加振动后材料的流动应力发生振荡，应力振荡导致材料平均流动应力下降，即应力叠加效应。KIRCHENER等^[7]发现在塑性变形过程中施加振动后出现平均应力下降的现象。关于应力叠加效应的理论模型主要是基于低中频振动塑性加工中的弹黏塑性模型，何勍等^[8]推算出黏弹塑性状态下应力的求解方程，蔡改贫^[9]运用黏弹塑性本构关系实现了低频振动条件下塑性成形体积效应机理分析，王家鹏等^[10]在其基础上考虑软化效应揭示了线性强化材料在超声振动下的本构关系。

另一种即施加超声振动后出现的“软化”和超声振动停止后出现的“残余硬化”现象^[11]。关于这种现象一种观点认为由于施加超声振动后试样温度提高，从而导致材料产生热致软化，但在实验中并未观测到试样显著温升^[6]。还有一种观点，即发生声软化效应，高频振动可以显著软化金属材料，而无需大幅加热。姚喆赫等^[6]分别基于热激活理论和位错演化理论建立了声塑性模型，并通过高频振动压缩实验对所建立的本构模型进行了验证。PRABHAKAR等^[12]基于位错理论提出了可以表达应变率和振幅对应力影响关系的动力学模型。然而上述本构模型并不能体现出材料外部特征尺寸与材料内部微观结构的长程相互影响。

由以上学者的研究可以看出，超声振动塑性成形中，超声软化作用机制包括应力叠加、超声减摩、热致软化、声软化以及声残余硬化。但由于在振动拉伸过程中，并不涉及模具和试样间的相对运动，同时在振动拉伸过程中也未观测到明显的温升，因此，为了定量描述超声(20 kHz)振动对AZ31B镁合金材料的变形行为的影响，这里暂不考虑温升导致的材料软化，建立一种应力叠加效应和声塑性效应混合的本构模型。各效应对于材料流动应力的影响如图1所示。

图1  超声振动“体积效应”

Fig. 1  “Volume effect” of ultrasonic vibration(UV)

其中应力叠加模型可由金属材料弹塑性解释，并未造成材料塑性变形机制或材料参数的变化。先从非局部理论角度出发，考虑外部特征尺寸对材料内部微观结构的长程相互影响，建立非局部应力叠加模型。然后，基于热激活理论和位错演化理论建立声塑性模型，考虑声软化和声残余硬化对材料流动应力的影响(声塑性模型：Ⅰ声软化；Ⅱ声残余硬化)。最后，在非局部应力叠加模型的基础上折减去声塑性导致的流动应力变化(非局部模型：Ⅲ应力振荡导致的应力下降)来预测超声振动对AZ31B镁合金的本构行为的影响，为超声振动下AZ31B镁合金的定量研究提供理论依据。

1  应力叠加效应模型的建立

应力叠加效应是由于金属材料在振动过程周期性的加载和卸载所引起的，可以认为：应力叠加效应必然存在于超声辅助金属塑性成形过程中。

1.1  非局部应力叠加效应理论模型

根据万有引力定律，考虑物质内部原子之间的作用力即“物质内部一点的应力是与它周围的原子相关的”。因此，根据EAVES 等^[13]和ERINGEN ^[14]的观点，可将非局部本构方程表达为一个卷积型的积分形式。本研究主要针对金属材料塑性变形阶段展开分析讨论，在塑性变形阶段考虑非局部效应，其非局部模型^[15]中非局部内变量表达为：

           (1)

式中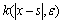：为弹性核函数；为Dirac Delta函数；为局部应力；为非局部剩余应力；0≤q≤1，当q=0时只考虑局部塑性，q=1时只考虑非局部塑性；x和s为物体内任意物质点坐标；取超声振动下轻合金材料的非局部核函数^[16]为：

                   (2)

特征参数在通常情况下依赖于材料内部特征长度与外部特征尺寸之比，= a/l，其取值范围为0~1。

在超声激励研究中，ERINGEN^[14]对外载荷定义包括(外载荷分布区域尺寸、波长、频率等)与超声激励有关的影响参数有频率、波长以及振幅，其中频率、波长和振幅均不能直接作为外部特征尺寸引入。而内部特征尺寸a为AZ31B镁合金晶粒尺寸，对于超声频率则是取一频率值作为基准频率值，以实际激励频率值与基准激励频率的比值这个无量纲量作为振幅的指数引入^[16]。具体形式如下：

                              (3)

超声激励下的非局部核函数如式(4)所示：

          (4)

式中：f_s为超声振动频率；f_n为基准频率；a为材料内部特征结构参数；A为超声振动振幅；为f_s的影响参数。

在此取核函数的积分值，定义衰减率，则h是关于作用域、振

幅A、以及振动频率f_s的函数，作为弹性核函数的积分值，定义h作为作用域加权平均或非局部衰减率，由于本文主要研究振幅变量对本构关系的影响，因此定义作为频率影响系数，通过超声激励下单向拉伸实验获得的有/无超声振动流动应力进行比较，反求影响系数g。

                    (5)

这里只考虑非局部效应，在此q值取1，式(1)简化为：

                   (6)

式中：为塑性阶段真实应力-应变曲线关于振幅A的函数，可由实验曲线拟合得到。

由于不同工艺对晶粒尺寸影响较大，为了获得真实的内部特征尺寸，对拉伸后的镁合金AZ31B棒材进行显微组织观察，发现其晶粒大部分在10~100 μm尺寸范围内，根据截线法估测其平均晶粒尺寸为50 μm，因此本研究中近似取a=50 μm。

取式(5)定义的核函数积分值反求获得的影响系数g的值如表1所示。

根据式(5)的定义，利用Matlab可获得核参量ε对衰减率h的影响，如表2所示，定义t为长程力学效应影响域，衰减快慢随离开源点x的距离远近变化，其中t=r / a (即区间)。当r→0时，核函数就变为，本构关系就成为广义Hooke定律。其中长程力学效应影响域h(t)分别取0.0002、0.001、0.005、0.01。

表1  超声激励对核参量ε的影响

Table 1  Effect of UV excitation on nuclear parameters

表2  超声激励对衰减率h的影响

Table 2  Effect of UV excitation on attenuation rate h

由表2可以看出，随着振幅的增大，即外部特征尺度与内部特征尺度取向接近的过程中，核参量ε随振幅的增大而增大，非局部衰减率h减小，即非局部效应增强。根据各参量随振幅的变化规律，取长程力学效应影响域t=0.01，计算流动应力随振幅A变化规律为：

            (7)

衰减率h的值随着振幅的增大，衰减率大致呈线性降低趋势，非局部应力变化规律与衰减率一致，这与王家鹏等^[10]得到的应力叠加效应随着振幅增大而流动应力下降的规律一致，证明了应力叠加效应理论模型的准确性。

1.2  应力叠加效应模拟验证

在本小节的数值模拟中并没有考虑声软化、声残余硬化以及温升变化等对材料流动应力的影响，成形载荷的变化完全由材料弹塑性特性所导致的应力振荡所决定，可以直接反应振动时应力叠加效应导致的流动应力变化。

因此，本节利用Abaqus有限元软件，对振动拉伸实验过程进行数值模拟分析。根据实际样件尺寸(直径d₀=6 mm，标距L₀=30 mm)，建立试样、上下夹头模型，试样零件属性为变形体，上下夹头设置为轴对称解析刚体，如图2所示，其中上下夹头与试样夹持端设置为绑定约束。在上夹头施加固定约束，并在上夹头端面施加20 kHz超声振动，下夹头施加3 mm/min的恒定速率向下运动，一直持续于整个模拟过程。 设置AZ31B镁合金的材料属性如表3所示。

图2  拉伸试样

Fig. 2  Tensile samples

表3  AZ31B的材料属性

Table 3  Material properties of AZ31B

材料的塑性参数按照无振动时单向拉伸实验中所得的真实应力-应变数据定义。参考实际拉伸实验，在拉伸10 s开始施加振动，持续时间3 s。因此，将Dynamic/Explicit模拟分析分为三个Step，均开启几何非线性，其具体设置如表4所示。

表4  振动拉伸模拟分析步设置

Table 4  Simulation step setting of UV tensile

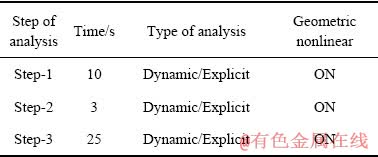
模拟中，仅在Step-2分析步中按照幅值曲线施加周期性的上下振动于上夹头；幅值曲线解析式为Asinωt，A为振幅，ω=2πf，f为振动频率。

图3所示为有限元模拟振动频率20 kHz、振幅A=7.12 μm时获得的拉伸真实应力-应变曲线。由图3可以看出，在施加超声振动时，材料的平均流动应力有显著下降。同时可以看出在有限元模拟中，振动时间对模拟结果的影响，施加振动的瞬间应力有大幅下降现象，过短振动时间不足以反映应力叠加效应应力下降值，长时间振动也会导致模拟结果失真。应选取中间平稳振动段的平均值来反映应力叠加效应导致的应力降幅。

图3  拉伸模拟真实应力-应变模拟曲线

Fig. 3  True stress-strain simulation curve in tensile simulation

以频率为20 kHz为例，提取模拟结果中不同振幅条件下真实应力应变曲线如图4所示。由模拟结果可知，当施加振动激励瞬间，应力迅速剧烈下降，然后短暂大幅度振荡回复至某一平衡位置，并开始周期性振荡。当振动激励停止时应力并没有立即回复到无振动路径，而是沿着弹性路径回复到无振动拉伸的应力水平，这与文献[17-18]中检测到的超声振动停止后出现一段斜线恢复上升现象一致。

对模拟结果中所对应的振荡段进行分析，取平稳阶段(去除施加振动瞬间大幅振荡段和振动后期的大幅振荡段)数据进行滤波处理，并进行曲线拟合。再将振荡段拟合得到的曲线与无振荡段拟合曲线进行对比，获得模拟振动流动应力平均降幅与理论推导流动应力降幅，如图5所示。

由图5可知，基于非局部思想建立的非局部应力叠加理论模型预测结果与应力叠加机制导致的流动应力模拟降幅基本一致，验证了非局部应力叠加模型的准确性，同时也得到流动应力下降规律：应力叠加效应导致的流动应力降幅与超声振幅成正比。

2  声塑性模型的建立

图4  不同振幅下模拟降幅

Fig. 4  Simulated decrease under different amplitudes

图5  超声振动应力叠加效应下模拟与理论应力降幅

Fig. 5  Simulation and theoretical stress reduction caused by stress superposition effect

声软化效应理论模型基于热激活模型的晶体塑性理论模型^[19]上建立。首先，通过泰勒模型建立起多晶体单轴应力-应变之间的关系来研究晶体微观滑移机制和应力-应变之间的关系：

                                 (8)

式中：M为泰勒因子，也称取向因子；为流动应力；为塑性应变；为激活滑移系中的临界剪切应力；为激活滑移系中的临界剪切应变。

基于热激活理论：

                       (9)

式中：为越过障碍所需的总激活能；k为Boltzmann常数；T为热力学温度；为频率因子；为剪切塑性应变率。

图6所示为施加9.63 μm超声振幅时振动拉伸过程中利用FLIR TG165红外热像仪检测到的温度场变化(实验在室温20 ℃条件下进行)。

图6  振动拉伸过程温度场变化

Fig. 6  Temperature field changes during UV stretching

在使用最大振幅(9.63 μm)进行振动拉伸时，并未观测到明显的温度变化，温升最大仅有3.5 ℃，并且从温度场的分布可以看出该温度变化主要由变幅杆的热传导所致。显然3.5 ℃的温升并不足以引起流动应力的显著下降。因此超声振动对于T的影响较小，声软化效应主要归因于和对于超声激励的响应。

令，则式(9)化为：

                               (10)

无量纲应力比仅取决于W，即

             (11)

式中：为无振动条件下应力比；为超声辅助下应力比；为超声振动引起的净变化量；E为声能密度；、m分别为基于实验待确定参数。

                            (12)

式中：为机械阈值，其物理意义为在绝对零度条件下的材料剪切强度；为晶格阻力；为剪切弹性模量；为参数接近1/3；b为Burgers矢量长度；为位错密度。

超声能量密度E满足如下关系式^[20]：

                                (13)

式中：为角频率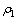；为材料密度。

模型中的待定参数通过无振动条件下单向拉伸实验确定，所得参数列与表5。

材料内部位错密度等缺陷在超声激励下的累积将会导致材料的硬化，超声能场作用后材料的声残余硬化效应是一种永久性硬化，因此，可将其可归因于材料内部位错的变化。超声能场作用下的位错演化机制为：

              (14)

式中：k₁为位错存储系数，实验识别；k₂为动态恢复系数，实验识别；η_k1为在超声作用下k₁的变化比率，与位错增殖有关；η_k2为在超声作用下k₂的变化比率，与位错湮灭有关。

   由于在本研究中未检测到声残余软化现象，因此忽略η_k2。

                     (15)

式中：t_v为超声振动持续时间30 s；P₀为η_k1的初始值，实验识别；K为η_k1的极限值，实验识别；r为增长率，主要受超声能场强度影响，本研究中r正比于振幅A，比值为，实验识别。

表5  声塑性模型中的参数数值

Table 5  Parameter values in acoustic plastic model

不同超声振动作用后材料内部位错演化规律可以通过薄膜透射技术进行观测。图7所示为取不同超声振幅(5.81、7.12、8.41和9.63 μm)振动条件下拉伸试样制样，并利用JEM 2100 Plus透射电镜观测到的AZ31B镁合金拉伸试样透射组织。

通常，晶体中的位错密度表示为：

                                    (16)

式中：L₀为晶体中位错总长度；V为晶体体积。

为了简便，位错密度还可以表示为：

                               (17)

式中：S为位错线横截于晶体的表面积；n为位错露头数；L₀为晶体长度，也就是每根位错线长度。

通过统计估测出的位错线总长度、试样厚度，根据式(17)计算位错密度随振幅变化规律如图8所示。

在图8中可以看出，在不同超声振动振幅条件下，位错在晶界处都出现不同程度的塞积。但是位错的塞积程度是随着振幅的提高而加剧的，位错在晶界处严重堆垛塞积形成位错墙阻碍塑性流动，位错的可动性降低材料塑性变低。这也说明超声激励对于位错的增殖和再分布起正面作用，这一推断为实验^[24]所证实。

图7  不同振幅A下拉伸试样位错分布的TEM像

Fig. 7  TEM images of dislocation distribution of tensile specimen under different amplitudes

图8  拉伸试样位错密度随振幅A的演变规律

Fig. 8  Dislocation density of tensile specimen changes with amplitude

3  理论推导结果与振动拉伸实验验证

3.1  理论推导结果

综合考虑非局部应力叠加效应及声塑性效应导致的流动应力变化，最终拟合得到超声振动条件下AZ31B镁合金本构关系：

       (18)

3.2  振动拉伸实验验证

振动拉伸实验设备如图9所示。支撑架通过螺栓固定安装在WDW-100kN型电子万能试验机的上方固定横梁。换能器与变幅杆通过双头螺柱连接，变幅杆通过法兰固定在支撑架上，试样一端通过螺纹连接到变幅杆上，另一端通过WDW-100kN型电子万能试验机夹持在拉伸机下方移动横梁上。选择拉伸速度3 mm/min，振动频率通过超声振动设备自动扫频得到为20 kHz，振幅通过调节超声波发生器控制面板上功率旋钮，利用OPTOMET数字激光测振仪获得20%、40%、60%和80%满载功率时输出振幅A分别为5.81、7.12、8.41和9.63 μm。为了保证超声振动辅助成形实验数据的可靠性，每种加载条件下至少要做3次实验。

图9  振动拉伸实验设备

Fig. 9  UV tensile testing equipment

通过拉伸实验机提供的原始数据，获得不同振幅下真实应力-应变曲线变化规律如图10所示。

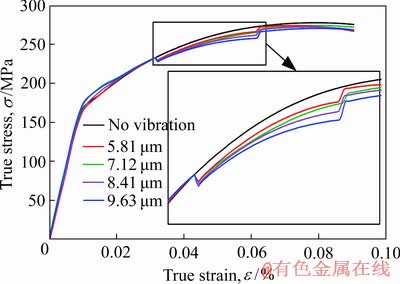
图10  不同振幅A下镁合金AZ31B真实应力-应变曲线

Fig. 10  True stress-strain curve of AZ31B alloy at different amplitudes

由实验数据可以清楚的看到AZ31B镁合金在施加超声振动后，流动应力立即下降，且流动应力下降量与超声振幅呈正比，与此同时，也可以清楚的看到，超声振动停止后，材料的残余硬化也随着超声振幅的增大而越来越严重。超声振动残余硬化正是由于材料吸收超声能量，使得位错更易克服钉扎效应转变为可动位错，大量的位错运动导致位错在晶界处塞积、堆垛形成位错墙和孢状结构，阻碍材料流动，且这一现象随着超声振幅的提高越来越显著。这一推断已在图7所示的不同振幅条件下位错分布图所证实。

图11  超声振动理论与实验应力降幅对比

Fig. 11  Comparison of UV theoretical and experimental stress reductions

根据式(18)将超声振动振幅为9.63 μm时的理论值计算值与实验曲线进行对比如图11所示。由图11可知，根据理论模型计算所得应力下降情况与实际实验情况流动应力下降情况基本一致。考虑应力叠加效应、声软化和声残余硬化效应所建立的本构模型能够准确表达AZ31B镁合金材料对于超声激励的响应。

4  结论

1) 本文考虑材料应力叠加效应、声软化、以及声残余硬化效应建立的AZ31B镁合金本构模型，能够准确表达AZ31B镁合金材料对于超声激励的响应。

2) 基于非局部思想建立的应力叠加理论模型能够很好地描述材料受到超声激励后材料流动应力发生机械振荡而出现的变化。且结果表明，应力叠加效应导致的流动应力的变化与超声振幅成正比。

3) 通过在热激活晶体塑性理论模型中引入超声能场参数，可以方便地进行声软化效应的理论建模，解释声软化效应。

4) 声残余硬化效应主要是由于超声激励后材料位错密度的累积造成的。超声作用可以增强位错的增殖和再分布，随着超声作用时间的延长以及材料变形程度的加剧，材料内部位错密度均出现不同程度的塞积，使材料宏观出现“硬化”的现象。

REFERENCES

[1] 余 琨, 黎文献, 王日初, 马正青. 变形镁合金的研究、开发及应用[J]. 中国有色金属学报, 2003, 13(2): 277-288.

YU Kun, LI Wen-xian, WANG Ri-chu, MA Zhen-qing. Research, development and application of wrought magnesium alloys[J]. The Chinese Journal of Nonferrous Metals, 2003, 13(2): 277-288.

[2] IMAM F E R, JAMIL M S C, SAMAD Z,SHEIKH M A,NAJIBA M. Influence of non-conventional beam profile on edge effects in laser forming of AISI 304 stainless steel plate[J]. The International Journal of Advanced Manufacturing Technology, 2019, 104(1/4): 1593-1601.

[3] LIU Ning, LAI Zhi-peng, CAO Quan-liang, HAN Xiao-tao, HUANG Yu-jie, LI Xiao-xiang, CHEN Meng, LI Liang. Effects of air on metallic sheet deformation by electro- magnetic forming[J]. The International Journal of Advanced Manufacturing Technology, 2019, 103(1/4): 311-324.

[4] CAO Miao-yan, LI Jian-chao, YUAN Ya-ning, ZHAO Chao-cai. Flexible die drawing of magnesium alloy sheet by superimposing ultrasonic vibration[J]. Transactions of Nonferrous Metals Society of China, 2017, 27(1): 163-171.

[5] WEN Tong, GAO Rui, CHEN Xia. Influence of high frequency vibration on deep drawing process of AZ31 sheet at room temperature[J]. Journal of Shanghai Jiao Tong University (Science), 2012, 17(4): 456-460.

[6] 姚喆赫, 陈子辰, 梅德庆. 超声能场在金属微/介观成形中的作用理论及实验研究[J]. 机械工程学报, 2018, 54(1): 98.

YAO Zhe-he, CHEN Zi-chen, MEI De-qing. Theoretical and experimental studies on effects of ultrosonic energy field in micro/meso metal forming[J]. Journal of Mechanical Engineering, 2018, 54(1): 98.

[7] KIRCHNER H O K, KROMP W K, PRINZ F B, TRIMMEL P. Plastic deformation under simultaneous cyclic and unidirectional loading at low and ultrasonic frequencies[J]. Journal of Materials Science, 1985, 68(2): 197-206.

[8] 何 勍, 闻邦椿. 金属振动塑性加工中体积效应的机理分析[J]. 金属成形工艺, 1998, 16(6): 35-36, 47-48.

HE Qing, WEN Bang-chun. Mechanism analysis of volume effect in metal vibration plastic machining[J]. Journal of Netshape Forming Engineering, 1998, 16(6): 35-36,47-48.

[9] 蔡改贫, 姜志宏, 翁海珊. 低频振动塑性成形粘弹塑性模型的体积效应分析[J]. 机械强度, 2007, 29(2): 346-350.

CAI Gai-pin, JIANG Zhi-hong, WEN Hai-shan. Volume effect analysis of visco-elasticity plasticity models for plastic deformation with low-frequency vibration[J]. Journal of Mechanical Strength, 2007, 29(2): 346-350.

[10] 王家鹏, 赵 震, 庄新村, 柏 杨. 超声振动辅助成形本构模型[J]. 塑性工程学报, 2015, 22(6): 1-6.

WANG Jia-peng, ZHAO Zhen, ZHUANG Xin-cun, BAI Yang. Study on constitutive model of ultrasonic vibration assisted forming[J]. Journal of Plasticity Engineering, 2015, 22(6): 1-6.

[11] SIU K W, NGAN A H W. Understanding acoustoplasticity through dislocation dynamics simulations[J]. Philoso-phical Magazine, 2011, 91(34), 4367-4387.

[12] PRABHAKAR A, VERMA G C, KRISHNASAMY H, PANDEY M P, LEE M G, SUWAS S.Dislocation density based constitutive model for ultrasonic assisted deformation[J]. Mechanics Research Communications, 2017, 85:76-80.

[13] EAVES A E, SMITH A W, WATERHOUSE W J, SANSOME D H. Review of the application of ultrasonic vibrations to deforming metal[J]. Ultrasonics, 1975, 13(4): 162-170.

[14] ERINGEN A C. Nonlocal Continuum Field Theories[J]. Rheologica Acta, 1991, 30(1): 23-32.

[15] LU X L, BARDET J P, HUANG M S. Numerical solutions of strain localization with nonlocal softening plasticity[J]. Computer Methods in Applied Mechanics and Engineering, 2009, 198(47/48): 3702-3711.

[16] 卞平艳, 赵 波. 基于非局部理论的纳米复相陶瓷超声磨削试验研究[J]. 硅酸盐通报, 2013, 32(3): 512-517, 522.

BIAN Ping-yan, ZHAO Bo. Experimental research ultrasonic grinding of nano-composite ceramics materials based on nonlocal theory[J]. Bulletin of the Chinese Ceramic Society, 2013, 32(3): 512-517, 522.

[17] DAUD Y, LUCAS M, HUANG Z H. Modelling the effects of superimposed ultrasonic vibrations on tension and compression tests of aluminium[J]. Journal of Materials Processing Tech, 2006, 186(1): 179-190.

[18] DAUD Y, LUCAS M, HUANG Z H. Superimposed ultrasonic oscillations in compression tests of aluminium[J]. Ultrasonics, 2006, 44(1): E511-E515.

[19] SIDDIQ A, SAYED T E. Acoustic softening in metals during ultrasonic assisted deformation via CP-FEM[J]. Materials Letters, 2010, 65(2): 356-359.

[20] YAO Z H, KIM G Y, WANG Z H. Acoustic softening and residual hardening in aluminum: Modeling and experiments[J]. International Journal of Plasticity, 2012, 39: 75-87.

[21] HAASEN P. Physical Metallurgy[M]. Cambridge: Cambridge University Press, 1996: 113-124.

[22] CUBBERLY W H, BAKER H, BENJAMIN D. Metals handbook(Ninth ed, Volume 2). Properties and selection: Nonferrous alloys and pure metals[M]. Ohio: American Society for Metals, 1984: 125.

[23] FRANOIS D, PINEAU A, ZAOUI A. Mechanical behavior of materials[M]. Dordrecht: Kluwer Academic Publishers, 1998: 87.

[24] PESLOA A. Ultrasonic hardening of aluminium alloys[J]. Ultrasonics, 1984, 22(1): 37-41.

Constitutive relationship of AZ31B magnesium alloy under ultrasonic vibration

CAO Miao-yan^{1, 2}, TIAN Shao-jie^{1, 2}, HU Han^{1, 2}, ZHAO Chang-cai³, HAN Xu-bin³

(1. College of Mechanical Engineering, Yanshan University, Qinhuangdao 066004, China;

2. Hebei Innovation Center for Equipment Lightweight Design and Manufacturing, Qinhuangdao 066004, China;

3. Key Laboratory of Advanced Forging Technology and Science of Education Ministry (Yanshan University), Qinhuangdao 066004, China)

Abstract: The studies of theory, experiment and simulation were carried out for exploring the “Volume Effect” rule and mechanism of ultrasonic vibration(UV) in plastic forming of magnesium alloy AZ31B. Firstly, the stress superposition model of UV for magnesium alloy AZ31B was established based on non-local theory. And the model was verified by simulation. Then, the UV acoustic plastic model of magnesium alloy AZ31B was established based on thermal activation theory and dislocation evolution theory. The accuracy of the model was verified by the experimental data. The results show that the stress drop is linearly and positively correlated with the UV amplitude. The stress superposition effect model and the harmonic plastic effect model can describe the stress dropping in the ultrasonic assisted forming. The superposition effect causes the average flow stress of the material to oscillate and decrease. Acoustic softening effect refers to the dislocation absorbs ultrasonic energy to overcome the nailing effect, which is beneficial to the plastic deformation of the material. Acoustic residual hardening effect mainly reflects in the high ultrasonic energy leading to a large number of dislocation density proliferation. The dislocation plugs up at the grain boundary to form a dislocation wall, causing the material flow to be blocked. Eventually, the material shows residual hardening.

Key words: ultrasonic vibration; effect of stress superposition; effect of acoustic plasticity; constitutive model

Foundation item: Projects(51775480, 51605420) supported by the National Natural Science Foundation of China; Project(E2018203143) supported by the Natural Science Foundation of Hebei Province, China

Received date: 2019-07-09; Accepted date: 2020-04-28

Corresponding author: CAO Miao-yan; Tel: +86-335-8061730; E-mail: jacmy@ysu.edu.cn

(编辑  何学锋)

基金项目：国家自然科学基金资助项目(51775480，51605420)；河北省自然科学基金资助项目(E2018203143)

收稿日期：2019-07-09；修订日期：2020-04-28

通信作者：曹秒艳，教授，博士；电话：0335-8061730；E-mail：jacmy@ysu.edu.cn