共晶和包晶合金定向凝固过程中共生生长的形态稳定性
来源期刊:中国有色金属学报2006年第7期
论文作者:苏彦庆 骆良顺 毕维生 郭景杰 傅恒志
文章页码:1125 - 1135
关键词:共晶合金; 包晶合金; 共生生长; 形态稳定性
Key words:eutectic alloy; peritectic alloy; coupled growth; morphological stability
摘 要:近年来对共晶合金共生(耦合)生长形态稳定性的研究取得了一系列重要的成果。 这些成果主要包括: 片层共晶共生生长在最小过冷度下的超稳定性、 片层共晶共生生长的Z字形分叉、 熔体流动及非线性动力学对共生生长形态稳定性的影响等。 在此基础上人们又开始关注包晶合金定向凝固中的稳态共生生长及其形态稳定性。 综述了这些研究成果, 并对其发展方向进行了探讨。
Abstract: The achievements of recent extensive experimental and theoretical researches on the morphological instabilities of eutectic and peritectic coupled growth were reviewed. The predominant findings are: the overstability below the minimum undercooling spacing of eutectic coupled growth, zigzag bifurcation in bulk lamellar eutectic coupled growth, influences of fluxion in melts and nonlinear dynamics upon the morphological instabilities of coupled growth, and morphological stability of isothermal and non-isothermal peritectic coupled growth, and the similarities and differences between peritectic and eutectic coupled growth. The prospective directions of morphological stability of coupled growth were discussed.
文章编号: 1004-0609(2006)07-1125-11
苏彦庆, 骆良顺, 毕维生, 郭景杰, 傅恒志
(哈尔滨工业大学 材料科学与工程学院, 哈尔滨 150001)
摘 要: 近年来对共晶合金共生(耦合)生长形态稳定性的研究取得了一系列重要的成果。 这些成果主要包括: 片层共晶共生生长在最小过冷度下的超稳定性、 片层共晶共生生长的Z字形分叉、 熔体流动及非线性动力学对共生生长形态稳定性的影响等。 在此基础上人们又开始关注包晶合金定向凝固中的稳态共生生长及其形态稳定性。 综述了这些研究成果, 并对其发展方向进行了探讨。
关键词: 共晶合金; 包晶合金; 共生生长; 形态稳定性
中图分类号: TG111.4 文献标识码: A
SU Yan-qing, LUO Liang-shun, BI Wei-sheng, GUO Jing-jie, FU Heng-zhi
(School of Materials Science and Engineering, Harbin Institute of Technology,
Harbin 150001, China)
Abstract: The achievements of recent extensive experimental and theoretical researches on the morphological instabilities of eutectic and peritectic coupled growth were reviewed. The predominant findings are: the overstability below the minimum undercooling spacing of eutectic coupled growth, zigzag bifurcation in bulk lamellar eutectic coupled growth, influences of fluxion in melts and nonlinear dynamics upon the morphological instabilities of coupled growth, and morphological stability of isothermal and non-isothermal peritectic coupled growth, and the similarities and differences between peritectic and eutectic coupled growth. The prospective directions of morphological stability of coupled growth were discussed.
Key words: eutectic alloy; peritectic alloy; coupled growth; morphological stability
具有两固相α, β和一个液相L三相平衡的共晶合金和包晶合金对于传统的铸造、 焊接乃至先进的超导体晶体生长都具有重要的应用[1]。 理论上讲, 在平衡点以外共晶和包晶合金形成两固相的原位混合物在热力学上都是可能的。 这种原位的混合物是两固相通过液相来交换溶质原子而产生的, 这个过程就是扩散控制的共生(耦合)生长[2]。 如果共生产生的两相(或几相)能实现规则分布, 就可以制备出具有多种特殊性能的材料, 它们已在磁学、 光学、 结构材料等领域发挥出重要作用, 并将随着理论与技术的发展而进一步挖掘其应用潜力[3]。
共晶共生生长在理论和实验上研究得已非常深入, 各种理论也比较成熟, 片状和纤维共生组织可以利用Jackson-Hunt(以下简称JH)理论很好地描述[4]。 但是, 对共生结构形态稳定性的理解仍然很欠缺, 尤其是在二维和三维情况下。 虽然JH理论预测共晶共生相间距在λm〈λ〈λM时共生形态是稳定的(λm和λM分别为最小和最大的稳定片层间距)[4], 但由于JH理论采用平界面等过于理想的假设, 使其关于共生形态稳定性的预测与实验有较大的差距, 特别是当合金成分远离共晶点时[5]。 为了深入理解形态稳定性的本质, 许多研究者利用实验[6-15]、 理论分析[16-24]和数值模拟[25-29]对共生行为进行研究。 近年来取得了许多重要的成果, 主要包括: 片层共晶共生在最小过冷度下的超稳定性[1, 30]、 片层共晶共生的Z字形分叉[31]和片层共晶共生的熔体流动与非线性动力学的耦合[32-34]。
包晶合金能否发生稳态共生生长是一个困扰了人们40多年的理论问题[1]。 近年来在Cu-Zn[35-38]、 Ti-Al[39-40]、 Fe-Ni[41-44]、 Ni-Al[45]等包晶系中发现的共生组织引起了人们对该问题很大的兴趣。 一方面与共晶共生行为的对比可以丰富凝固理论, 另一方面许多重要的合金系, 如Ti-Al、 Ni-Al、 Fe-Al都具有包晶反应[46]。 如何得到规则排列的两相组织以提高这些合金的综合性能是目前的一个重要研究方向。 这些都需要人们深入地研究包晶系的共生行为。 而共生行为的核心就是共生形态稳定性问题。 本文作者将对共晶和包晶共生生长的形态稳定性的最新研究成果作简要评述, 并对其发展方向做一些初步的探讨。 由于近年来对纤维共生的研究仍是从共生两相的体积分数差异着手, 所以本文的论述主要集中在片层共晶共生。
1 共晶共生生长的形态稳定性
1.1 Jackson-Hunt理论及其发展
1966年, Jackson和Hunt在对稳态共晶生长分析的基础上, 提出了经典的稳态共晶生长理论[4]。 JH理论最重要的结论就是得出共晶共生界面前沿的过冷度ΔT与共晶片层间距λ的关系式:
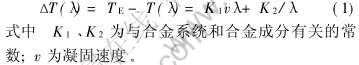
式(1)给出了宏观上平的共晶共生界面以v的速度推进时的过冷度与片层间距的关系。 式(1)右边的两项分别是由溶质扩散和界面张力作用引起的过冷度。 这两项的竞争作用产生了典型的ΔT(λ)曲线, 如图1所示。 对于共晶共生生长, ΔT(λ)曲线有一最小值λm为
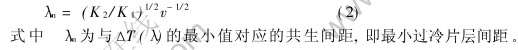
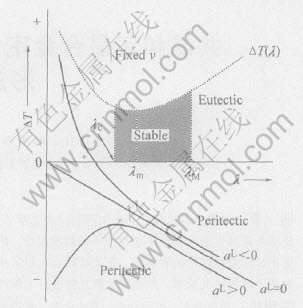
图1 共生界面前沿的过冷度随共生片层间距的变化
Fig.1 Variation of interface undercooling with lamellar spacing for given growth velocity
即最小过冷片层间距。
JH理论以简单的式(1)和(2)描述了共晶共生中的基本理论, 从中可以得到以下结论:
1) 一个特定的定向凝固系统以一特定的凝固速度v进行凝固, 最后进入到某个稳定状态, 共晶稳态共生间距λ(或称波长λ)不是被系统“独一无二”地确定了, 而是与系统的历史有关, 但是λ(或共生间距的平均值)的选择存在一个最可几分布, 即λ将趋近λm(最小过冷度理论)。
2) 在共晶稳态共生系统中, λ2v为常数, 与系统的温度梯度G无关。
3) 稳态共晶共生片层间距λ虽然有一最可几分布, 但是稳态共生有一稳定的片层间距范围(λm, λM)。 当λ〈λm和λ>λM共生都是不稳定的。 λ〈λm的不稳定性主要是局部的片层消失而增大λ; λ>λM的不稳定性主要是大片层尖端开裂而出现分叉, 并出现新的片层。
4) λM=Aλm, A为由合金成分决定的常数。
虽然JH理论与一系列的实验取得了较好的一致性[2], 但是由于JH理论采用了一些过于理想化的假设, 相对于实际凝固过程还有许多需要完善之处:
1) JH理论沿用Cahn对稳态共晶共生的假设(所以JH理论有时也被称为JH-Cahn理论): 共生为局部生长, 局部生长方向垂直于共生界面, 并且稳态共生存在一个最小的片层间距λc, JH认为λc=λm。
2) 纯扩散凝固, 利用二维的扩散场来解决共生稳定性问题, 未考虑熔体中的对流影响。
3) 假设共生界面为平界面, 至少在宏观尺度上是平界面。 宏观尺度是指远大于λ的尺度。
4) 过冷度不是很大或者凝固速度不是很快, 并在此条件下认为共生的两相α, β界面前沿的过冷度相等, 即ΔTα=ΔTβ。
5) 式(2)显示λ2v为常数, 且与系统的温度梯度G无关, 但是是否对所有的G都合适并不清楚。
6) JH理论预测了稳态共生间距和稳态间距之外的不稳定性, 但是稳态共生间距的取值是否准确以及稳态间距之外的不稳定演化机制尚不清楚。
为了解决以上问题, 更准确地认识共晶的稳态共生行为, 国内外许多研究者借助更精确的实验装置和功能更强大的计算机对共晶共生行为展开了深入的研究, 取得了一系列重要的研究成果。
2002年, Akamastsu等[30]在第一次精确测定共晶共生界面前沿过冷度的基础上, 全面考察了JH-Cahn理论, 发现共生片层在沿共生界面法向生长的同时还存在沿共生界面的滑动速度, 从而提出了共晶共生最小过冷度下的超稳定性理论(1.2节)。
实际的定向凝固系统中, 熔体中热溶质对流、 溶质密度差的存在将对纯扩散凝固过程中的溶质分凝产生影响。 Magnin和Trivedi[32]在JH理论的基础上, 引入了共晶两相密度差对共生界面前沿溶质分凝的影响:

他们对JH理论的改进只局限于共生的两相密度差对纯扩散凝固过程中溶质分凝的影响, 而实际的定向凝固系统中还存在热梯度引起的热溶质对流、 重力引起的自然对流等, 这些对流的存在必将对共晶共生的形态产生更重要的影响[33, 47-49](1.4节)。
为了消驰平界面假设, 研究凝固速度v和温度梯度G对JH理论的影响, 国内外学者都进行了深入的研究[6, 7, 50]。 Seetharaman和Trivedi[51]用实验证明稳态共晶共生区间落在JH理论预测的范围之内, 但是比JH理论预测的要小, 且平均间距比λm稍大。 他们发现, 当凝固速度减小时, 稳定区间增加。 由于JH理论只是在大的温度梯度形成的接近平界面时适用, 但是对大的温度梯度时, 对共生的两相的过冷度相等的假设却又不是很合适, 所以Kassner和Misbah[52, 53]对JH理论进行改进, 去掉了这些假设, 他们得出的结论主要为

他们对JH理论的改进使JH理论在中等温度梯度下界面并不接近平界面时也是适用的。 但是改进后的JH理论在温度梯度继续减小或凝固速度较大时界面出现分裂的时候又不太适用了, 此时就需要将JH理论推广到凝固速度较大的范围内。 Trivedi和Kurz等[54, 55]通过凝固速度对共晶液相线斜率m和有效溶质分配系数ke的影响及非平衡界面的动力学分析, 建立了与共晶Peclet数(P=v/2Dl)之间的关系, 发现共晶层片共生的最大速度取决于ke, 当ke→1时为过冷限机制, ke→0时为扩散系数机制。 然而, 随着凝固过冷度的增大, 共晶普遍存在规则向非规则共晶的转变, ΔT—λ曲线将显著偏离实验结果[56-59], 所以Trivedi和Kurz对JH理论的推广在过冷度较大时不再适用。 对此本文不再详述。
对于接近稳态共晶共生间距范围上限的不稳定性依然是人们目前研究的热点, 这主要是因为1987发现的稳态共晶共生的倾斜不稳定性[60]。 这种倾斜不稳定性与JH预测的振荡不稳定性的竞争与耦合激起了人们强烈的想全面了解共晶系统中完美对称性被破坏的演化机制的愿望[5, 61-66]。 近几年来, 人们利用实验和数值模拟在共晶共生间距范围上限的不稳定性也取得了许多重要的成果。
下面对这些重要的研究结果分别进行简要论述。
1.2 最小过冷度下的超稳定
JH-Cahn理论预测当λ>λm时, 共生生长的形态将是稳定的。 这是因为当λ>λm时, 共晶片层间距的减小会使界面过冷度沿着图1所示ΔT(λ)曲线下降, 这时这种扰动会及时减小。 与之相反, 当λ〈λm时, 共晶片层间距的减小将使界面的过冷度增大, 而界面过冷度的增大将使共晶片层进一步减小, 直到某个(些)片层从片层排列中消失, 从而使稳定后的片层间距增大。 1980年Langer[67]利用边缘稳定性原理证明这种极小值条件是边缘稳定的, 并给出扰动被放大引起片层消失的示意图, 如图2所示。 x1和x′1处的扰动被放大, 使两点产生相互趋近的运动, 从而使一片α消失, 并使重新稳定后的片层间距增大。 最近的研究[30]第一次直接在实验中测量出了有机共晶系的界面前沿的过冷度随片层间距变化的曲线, 并直接观察到了片层间距微小扰动的消退现象, 可是得出的结论却与上述的预言不符。 在上述实验中人们发现, 即使片层间距低至0.8λm时, 界面仍是稳定的。 这种超稳定现象与相场法模拟结果吻合很好[30]。 此外, 利用模拟结果分析发现, 这种超稳定性要归结于三相交点的复杂动力学。 这种新的发现使人们对界面的运动有了新的认识, 即三相交点在向前推进的同时, 还有一个平行于界面的与片层间距成比例的速度[30], 图3所示为共晶界面为凹的情况。 其中ζ(x)为共生界面与界面前沿温度为TE位置处的距离函数。 这种效应可以使片层间距均匀化, 并因此稳定界面。
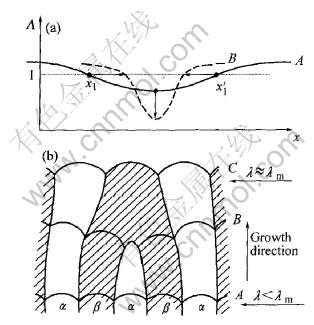
图2 不稳定的共晶共生界面上的扰动被放大引起片层消失示意图
Fig.2 Schematic illustration of one lamella terminated by unstable fluctuation[67]
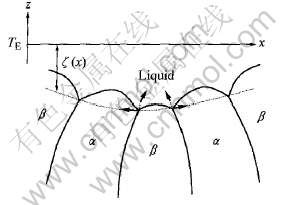
图3 共晶界面在凹的情况下片层间距运动示意图
Fig.3 Schematic illustration of lamellar evolution[1] (Dotted arrow depict motion of trijunctions normal to envelop; solid arrow indicate lateral motion of junctions in direction of increasing spacing)
定量地描述这种现象, 可以用推广Langer的片层间距的长波调整机制来描述[1, 67, 68]。 在层片共生生长过程中, 局部片层间距的变化是由扩散控制的:
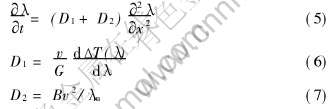
式(5)中片层间距的扩散由两部分构成, 第一部分是三相交点沿凝固方向运动产生的, 在Langer[67, 68]的分析中已经给出, 如式(6), 式中G为温度梯度; 第二部分, 如式(7), 是三相交点增加的横向滑动, 式中B为个根据实验和模拟结果拟和而得到的无量纲的常数。 当三相交点没有横向滑动时(即D2=0), 片间距随时间的变化将取决于D1。 由式(6)可见, D1与dΔT(λ)/dλ具有相同的符号。 所以当dΔT(λ)/dλ〈0时, 线性扰动将会被放大从而引起片层间距由于扩散而减小, 所以共生界面不稳定。 对于共晶合金, 即当λ〈λm时, 界面不稳定。 与之相反, 当三相交点存在滑动时(D2≠0), 当D1+D2〈0, 或λ〈λc时, 界面不稳定, λc为在超稳定性时共生片层的最小稳定间距, 由下式确定:
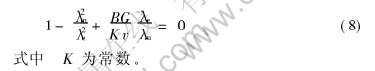
这说明最小的稳定片层间距是λc, λc小于最小过冷度理论的片层间距λm。 G/v越大, λc越小于最小过冷度下的片层间距, 即最小过冷度下的超过冷效应越显著。 此外, 不同合金系的超过冷效应很相似, 这样式(8)可以对超过冷效应有一个很好的预测。
1.3 大的间距稳定性: 倾斜与振荡
对于接近稳定片层间距上限的不稳定性, JH预测λ>λM的不稳定性主要是大片层尖端开裂而出现分叉, 并出现新的片层, 并且预测λM=Aλm, A为由成分决定的常数, 一般大于2 [69]。 1981年Dtye和Langer[68]在理论上发现了共晶共生在片层间距较大时会出现2λ振荡不稳定性(2λ Oscillatory-2λO, 即振荡的波长为片层间距的2倍)。 1987年Karma[60]利用数值模拟证实了这种2λ振荡, 并且发现了稳态共晶共生的倾斜不稳定性。 这个发现重新激起了人们从根本上研究共晶共生形态稳定性的兴趣[5, 69]。 经过十几年的研究, 现在对接近稳定片层间距上限λM的不稳定性, 得出的主要结论有:
1) 在稳态共晶共生生长时, 当共生间距超过一临界值λ0时, 可能会出现振荡不稳定性[69]: 包括1λ振荡和2λ振荡(图4), 但是出现振荡不稳定性时究竟是选择1λ还是2λ现在还不是很清楚。 有的研究者认为1λ振荡只在接近共晶成分的一个较小范围内出现, 并快速转变为1λ-2λ混合振荡, 而其他成分将会出现2λ振荡[5]。 有的研究者[69]在用CBr4-C2Cl6模拟共晶合金共生时发现在共晶成分附近, λ0≈1.2λm。 但是λ0是否是一个确定值以及在其他共晶系是否存在这种关系都是未知的。 振荡不稳定性的产生可能依然要归因于溶质边界层的影响[5], 但是具体产生的机制以及1λ和2λ的选择依然有待深入研究。
2) 当共生间距超过某一特定值λT时, 还可能会出现倾斜不稳定性(图4(d))。 在用CBr4-C2Cl6模拟共晶合金共生时发现[69], 在共晶成分附近, 均匀的倾斜分叉发生在λT≈1.9λm, 如果片层间距继续增大, 倾斜的均匀片层也可能发生振荡, 从而形成倾斜振荡组织。 定义片层的倾斜角为, 而tan=vd/v, vd为共生片层的侧向生长速度, 则一般在25°~35°变化。 倾斜不稳定性的出现可能是由于共生界面前沿的流动与溶质场的耦合, 但是具体形成机制目前尚不清楚。
3) 以上对振荡和倾斜稳定性的研究, 大都集中在共晶成分附近的低速共生区。 为了系统研究稳态共生的稳定性与共生间距λ、 凝固速度v以及合金成分c的关系, 许多研究者[5, 69]利用类共晶CBr4-C2Cl6进行了系统的研究, 他们做出了定向凝固共晶共生的稳定性图, 如图5所示。 稳定性图的坐标为η和Λ, 分别表征合金成分、 共生间距λ与凝固速度v对共生稳定性的影响:

由稳定性图可以清楚地确定稳态共生的存在区间, 从而控制凝固组织。
但是, 这种稳定性图的建立有不少局限性, 例如, 目前的大部分实验结果是通过观察薄长的类共晶CBr4-C2Cl6凝固而得到的, 而实践中需要考虑共晶合金在三维空间(至少是二维凝固界面)的稳定性, 此外目前对熔体中流动对共生稳定性的影响大都局限于定性描述。
1.4 熔体流动对共生形态稳定性的影响
共生界面前沿的熔体流动对共生的形态具有重[CM(22]要的影响, 例如熔体流动的存在将使共生间距增

图4 用CBr4-C2Cl6模拟共晶共生的大片层间距不稳定性
Fig.4 Morphological instabilities of lamellar eutectic
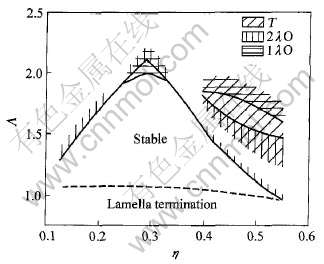
图5 定向凝固CBr4-C2Cl6类共晶合金共生生长的稳定性图
Fig.5 Stability diagram of directionally solidified CBr4-C2Cl6 eutectic[69]
大, 共生界面前沿的过冷度减小以及共生将向流动源方向倾斜等[33, 47, 49]。 在实际的定向凝固系统中, 由于试样不可能无限细, 热流也不可能是完全一维的, 会存在热溶质对流、 外加的扰动产生的对流等。 熔体中流动的存在必将对共生生长产生重要的影响。 下面简述这方面近年来得到的几个最典型的结论。
1981年Quenisset等[48]通过对Pb-Sn共晶系的研究, 发现当存在对流时, λ2v将不再是一常数, 而是对流流速梯度的函数:

Quenisset等[48]得到的式(11)第一次找到了共生形态与共生界面前沿熔体流动的定量关系, 并在在Pb-Sn共晶系得到了证实。 1998年, Ma等[47]利用渐进扩展的方法求解共晶合金小Peclet数定向凝固弱对流情况下的对流-扩散方程, 发现式(11)并不适合弱对流的情况。 他们得到的结果为

当对流较弱时, 式(12)能比较准确地反映对流对共生间距的影响。 2002年, Chen等[33, 34]在稳态共晶共生界面前沿引入流动, 利用非线性动力学求解了三相交点的运动方程, 发现当流动很小时, 共生间距在最小过冷度时与JH理论偏差不大; 而当流速很大时, 片层间距偏离JH理论较大, 可表示为

以上的研究结果建立了共生行为与熔体的流动强度之间的定量关系, 对认识凝固过程具有重要的参考价值。 由于熔体流动研究的本身非常复杂, 将其应用到凝固理论中难度比较大, 并且很难用实验来检验理论的正确性。 但是熔体中的流动对凝固过程的影响是广泛且重要的, 将流体动力学耦合到凝固理论中仍将是以后研究的一个重要方向。
1.5 二维共晶共生的形态稳定性: Z字形分叉
由于试验条件的限制, 以前人们对共生形态稳定性的理论研究都是局限于一维或准一维共生界面, 原位观察薄长(薄是指共生间距λ与试样厚度基本在一个数量级上)的共晶合金的共生行为[5]。 但是将上述情况下建立的共生稳定性理论用来分析一般定向凝固中的二维界面的稳定性经常会出现偏差[69]。 因此, 人们希望直接建立二维共生界面的稳定性理论。
2004年, Akamatsu等[31]建立了一套可以实时观察较大范围凝固界面的实验装置, 利用这套装置可以直接实时观察体积试样的定向凝固界面, 从而直接观察二维共生界面的形态稳定性。 他们利用这套装置研究了共晶成分附近的类共晶CBr4-C2Cl6的二维形态稳定性, 发现稳态片层共生的间距范围为(0.7λm, 0.85λm)。 当片层间距小于0.7λm时, 部分片层将消失从而增大平均片层间距, 这与一维的稳定性一致; 与一维稳定性不同的是, 当片层间距超过0.85λm时, 体积试样的共生界面将会出现Z字形分叉, 共生片层将会变得不规则, 如图6所示。 此外, 当片层间距λ超过1.1λm时, 片层结构将被破坏, 原始共生片层被破坏后一般会产生新的片层, 但是片层间距会减小。 普通的定向凝固一般都是针对体积试样的, 对比1.2节与1.3节可以看到, 这种试样定向凝固时共晶共生的稳定间距一般比薄长试样的稳定区间要小, 这可能是由于体积试样定向凝固时共生界面前沿更复杂的溶质场与流动相互作用的结果, 但是目前仍缺乏理论分析。
Akamatsu等[31]研究结果的意义远超过Z字形分叉本身, 他开辟了一种直接观察二维共生界面的试验方法, 从而为全面认识二维共生界面的形态稳定性打下了很好的基础, 并有可能将凝固理论的研究提升到一个新的水平。

图6 共生界面示意图及实时观察到的类共晶CBr4-C2Cl6定向凝固中的片层共生界面
Fig.6 Sketch of solid/liquid interface of lamellar eutectic (a), stable solid/liquid interface of CBr4-C2Cl6 eutectic (b) and zigzag bifurcation pattern of solid/liquid interface (c)[31]
2 包晶共生生长的形态稳定性
包晶合金是一类非常重要的合金, 许多铁基、 铝基、 铜基合金都包含包晶反应。 在近几十年里, 由于Ti-Al、 Ni-Al、 Fe-Al等具有重要工业应用前景的合金系[46]以及具有重要应用价值的Nd-Fe-B稀土永磁材料[70]、 Y-Ba-Cu-O高温超导材料[71]等在制备过程中都涉及到包晶反应, 使包晶合金的凝固行为成为凝固理论研究的热点[72]。 而对包晶合金的凝固行为研究的重点是包晶合金的凝固能否像共晶合金一样存在两相的共生生长。 这个困扰人们40多年的问题随着近年来在Cu-Zn[35-38]、 Ti-Al[39-40]、 Fe-Ni[41-44]、 Ni-Al[45]等包晶系中发现的共生组织再次引起了人们对该问题的关注。 然而能否像精确控制共晶共生一样来控制包晶共生从而得到具有特殊应用的组织这个问题又摆在了人们的面前。 而这个问题的本质便是包晶共生的形态稳定性。
2004年, Dobler等[41]通过实验和模拟研究了Fe-Ni包晶合金定向凝固过程中共生的稳定性。 他们发现稳态包晶共生产生的2个必要条件: 1)排出溶质多的相(一般为初生相)的生长形态是稳定的, 即该相的生长应该是稳定的平界面或胞状界面(此时的共生生长为非等温的弱耦合胞状共生生长); 2)包晶共生间距也存在一个稳定的范围(λmin, λmax), 共生间距应该落入这个稳定范围, 该范围由1λ振荡稳定性所确定。 这两个条件是必要的, 但是并不充分, 包晶共生的产生还需要有一定的起源条件来诱发。 他们认为包晶等温共生起源于岛状带组织, 具体演化机制为: 岛状带→1λ振荡组织→1λ振荡振幅逐渐减小→准稳态(稳态)包晶共生, 如图7所示。 通过实验和模拟, Dobler[41]发现包晶共生在接近λmin和λmax的不稳定性都是1λ振荡, 并确定了Fe-Ni合金包晶共生的稳定区间, 如图8所示。 由图可以看出: 当温度梯度G和凝固速度v确定时, 包晶共生的稳定性是合金成分和λ/lD的函数, λmin和λmax都随合金成分的降低而减小。 图中λm是利用将共晶模型引入到包晶模型中计算出的平均共生间距。 将共晶模型引用到包晶共生中, 得到的包晶共生的ΔT(λ)曲线如图1的下半部分。 图中aL是一个主要由合金成分决定的数, 对于k〈1的包晶系来说, 当aL>0, 由图可看出包晶合金共生生长时界面处于过热状态; 而aL〈0时, 当共生间距λ较小时界面过冷, λ较大时界面过热。 实验和模拟中发现, 包晶共生在界面过冷和过热时都可能稳定的进行, 并且稳定包晶共生时, ΔT-λ曲线的斜率dΔT/dλ〈0, 而这种情况按照传统的共晶稳定性理论来分析是不可能的。 因为如果产生共生间距减小的扰动会使界面过冷度继续增加(或界面过热减小), 这样共生间距会继续减小, 直到某些共生片
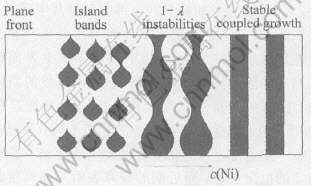
图7 Fe-Ni包晶合金定向凝固中共生的演化过程
Fig.7 Schematic representation of evolution with composition of microstructure of directionally solidified Fe-Ni alloy[41]
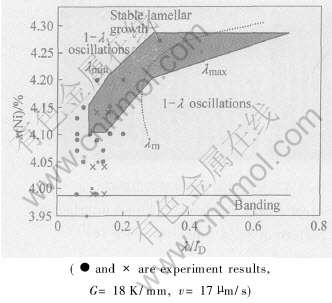
图8 Fe-Ni包晶合金的共生稳定区间
Fig.8 Stable lamellar coupled growth range (grey zone) as function of composition and lamellar spacing λ of Fe-Ni alloy[41]
层消失。 这种矛盾目前主要是通过引用产生最小过冷度下超稳定性的界面复杂运动来解释[1](1.2节)。 但是用界面的运动来解释包晶共生可以在过热情况下产生以及包晶共生的稳定性显得很薄弱, 因为式(7)中的影响超稳定性的主要参数是共晶共生模拟得出的常数B=0.18, 直接利用共晶系的参数B是否能够解释Fe-Ni包晶合金的稳态共生仍不能确定。 即使可以解释, 在其他包晶系中是否存在这种现象也是未知的, 所以仍需要进行很多基础性的研究。
通过对比包晶共生和共晶共生可以更深入地理解包晶共生。 目前的研究表明包晶共生和共晶共生具有以下异同[41]: 1) 包晶共生和共晶共生都是由界面张力作用和片层间的扩散之间的耦合而形成的; 2) 包晶共生和共晶共生都有两种共生形态, 片层和纤维, 这两种形态的转变都是由共生两相的含量差别引起的; 3) 包晶共生和共晶共生界面都存在侧向的溶质扩散; 4) 即使ΔT-λ曲线的斜率为负, 包晶共生和共晶共生在形态上都可能是稳定的; 5) 包晶共生和共晶共生的起源不同, 等温包晶共生一般起源于岛状带, 所以共生的两相一般没有特定的位向关系; 而近期的研究表明共晶共生起源于第二相在初生相上快速生长的形态不稳定性, 这也解释了为什么大部分共生片层具有相同的晶体取向[23]; 6) 包晶共生和共晶共生的形态稳定性不同, 共晶共生在小共生间距的不稳定性是长波不稳定性导致的片层消失, 在大共生间距的不稳定性是振荡(1λ或2λ)或倾斜, 振荡的波长由合金成分决定; 而包晶共生在小共生间距和大共生间距的不稳定性都是1λ振荡, 并且与合金成分无关。
目前对稳态包晶共生稳定性的研究仅仅刚刚开始, 仍处于机械借助共晶模型的阶段, 离准确认识和控制还有很长的距离。 但是随着具有包晶反应的合金和其他先进材料的日益应用, 无论是在理论上和生产实践中都需要对包晶共生进行更深入的研究。
3 结论
共生生长是一种非平衡、 非线性、 自组织过程, 并且共生生长形成的组织一般具有某些特殊的性能, 所以共生生长一直是凝聚态物理和凝固理论研究的重要对象。 共生生长的研究主要是通过研究其稳定性来准确控制共生行为。 目前共晶共生的研究已经相当深入, 并取得了很多重要的成果, 这些结果无论是对认识非平衡自组织这一物理现象还是控制凝固组织都具有重要的意义。 但是仍有很多理论还很不完善, 例如共晶共生的稳定性图还只是一个初步的设想, 并且有很多区域的不稳定性尚不清楚, 共生不稳定性与生长速度v、 温度梯度G、 合金成分c的关系, 二维界面稳定性的研究仅仅刚刚开始等问题仍需要继续研究。 包晶合金的共生行为的研究虽然也进行了很长的时间, 但是稳定共生在最近几年才得到明确的证实。 由于很多具有重要工业应用前景的结构材料如Ti-Al、 Ni-Al和Fe-Al等, 以及很多先进的功能材料的凝固过程都存在包晶反应, 无论从控制凝固组织还是丰富凝固理论角度出发, 包晶合金共生生长必将成为一个重要的研究方向。 为控制包晶共生生长必须对包晶共生形态稳定性进行深入的研究, 这些研究主要包括: 稳态包晶共生存在的热力学基础、 包晶共生的起源、 包晶共生的理论模型、 包晶共生的稳定间距范围以及稳定间距范围之外的不稳定性等。
REFERENCES
[1]Karma A, Plapp M. New insights into the morphological stability of Eutectic and peritectic coupled growth[J]. JOM, 2004(4): 28-32.
[2]Kurz W, Fisher D J. Fundamentals of Solidification[M]. Switzerland: Trans Pub Ltd, 1989. 94-106.
[3]李顺朴, 陈熙琛. 定向共晶复合生长的相形态控制[J]. 科学通报, 1995, 40(2): 109-111.
LI Shun-pu, CHEN Xi-chen. Control of the directional solidified eutectic phase morphology[J]. Chinese Science Bulletin, 1995, 40(2): 109-111.
[4]Jackson K A, Hunt J D. Lamellar and rod eutectic growth[J]. Trans Met Soc AIME, 1966, 236: 1129-1142.
[5]Karma A, Sarkissian A. Morphological instabilities of lamellar eutectics[J]. Metall Mater Trans A, 1996, 27(3): 635-656.
[6]姚向东, 黄韬, 周尧和, 等. 稳态层片共晶生长模型Ⅰ: 理论分析[J]. 自然科学进展, 1996, 6(6): 679-684.
YAO Xiang-dong, HUANG Tao, ZHOU Yao-he, et al. Model of steady lamellar eutectic growth Ⅰ: theoretical analysis[J]. Progress in Nature Science, 1996, 6(6): 679-684.
[7]姚向东, 黄韬, 周尧和, 等. 稳态层片共晶生长模型Ⅱ: 实验研究[J]. 自然科学进展, 1997, 7(1): 24-28.
YAO Xiang-dong, HUANG Tao, ZHOU Yao-he, et al. Model of steady lamellar eutectic growth Ⅱ: experimental research[J]. Progress in Nature Science, 1997, 7(1): 24-28.
[8]潘冶, 孙国雄. MnSb/Sb共晶复合材料与凝固界面稳定性[J]. 材料研究学报, 1999, 13(4): 359-363.
PAN Ye, Sun Guo-xiong. MnSb/Sb eutectic composites and solidifying interface stability[J]. Chinese Journal of Materials Research, 1999, 13(4): 359-363.
[9]潘冶, 孙国雄. 棒状共晶界面成分分布及对平界面生长的影响[J]. 铸造, 2000, 49(6): 315-317.
PAN Ye, SUN Guo-xiong. Solute distribution on interface of rod eutectic and its influence on plane interface growth[J]. Foundry, 2000, 49(6): 315-317.
[10]Mimmermann M, Karma A, Carrard M. Oscillatory lamellar microstructure in off-eutectic alloys[J]. Physical Review B, 1990, 42(1): 833-837.
[11]Han S H, Trivedi R. Banded microstructures formation in off-eutectic alloys[J]. Metall Mater Trans, 2000, 31(7): 1819-1832.
[12]Ludwig A, Generalised L S. ‘Jackson-Hunt’ model for eutectic solidification at low and large Peclet numbers and any binary eutectic phase diagram[J]. Mater Sci Eng A, 2004, 375: 540-546.
[13]Costa C A R, Batista W W, Rios C T, et al. Eutectic alloy microstructure: atomic force microscopy analysis[J]. Applied Surface Science, 2003, 240: 414-423.
[14]Bei H, George E P, Kenik E A, et al. Directional solidification and microstructures of near-eutectic Cr-Cr3Si alloys[J]. Acta Materialia, 2003, 51: 6241-6252.
[15]Aguiar M R, Caram R. Lamellar spacing selection in a directionally solidified Sn-Se eutectic alloy[J]. J Crystal Growth, 1997, 174: 70-75.
[16]李金富, 周尧和. 界面动力学对共晶生长过程的影响[J].中国科学(E辑), 2005, 35(5): 449-458.
LI Jin-fu, ZHOU Yao-he. Influence of interface dynamics on the eutectic growth[J]. Science in China (Ser.E), 2005, 35(5): 449-458.
[17]姚向东, 胡壮麒, 黄韬, 等. 纤维共晶生长界面前沿三维扩散场解析[J]. 材料研究学报, 1996, 10(2): 167-169.
YAO Xiang-dong, HU Zhuang-qi, HUANG Tao, et al. The analysis of three dimensional diffusion at fibrous eutectic growth front[J].Chinese Journal of Materials Research, 1996, 10(2): 167-169.
[18]马东, 介万奇. 定向规则共晶生长相间距的选择[J]. 金属学报, 1996, 32(8): 791-798.
MA Dong, JIE Wan-qi. Regular eutectic spacing selection during directional solidification[J]. Acta Metallurgia Sinica, 1996, 32(8): 791-798.
[19]潘冶, 孙国雄. 棒状共晶的凝固模型[J]. 金属学报, 1996, 32(2): 120-126.
PAN Ye, SUN Guo-xiong. Solidification model of rod eutectic[J]. Acta Metallurgia Sinica, 1996, 32(2): 120-126.
[20]Liu Jin-cheng, Elliott R. A numerical model for eutectic spacing selection in the CBr4-C2Cl6 eutectic system[J]. J Crystal Growth, 1995, 148: 406-414.
[21]ZHANG Wei-qiang, FU Hua, YANG Yuan-sheng, et al. A numerical model for spacing selection of lamellar eutectics grown from flowing liquids[J]. J Crystal Growth, 1998, 194: 263-271.
[22]Liu Jin-cheng, Elliott R. Selfconsistent solutions for lamellar eutectic growth[J]. Acta Materialia, 1995, 43(9): 3301-3311.
[23]Sridhar N, Rickman J M, Srolovitz D J. Microstructural stability of stressed lamellar and fiber composites[J]. Acta Materialia, 1997, 45(7): 2715-2733.
[24]Faivre G. Morphological instabilities of lamellar eutectic growth fronts: a survey of recent experimental and numerical results[J]. J Crystal Growth, 1996, 166: 29-39.
[25]朱耀产, 杨根仓, 王锦程, 等. 二元共晶定向凝固的多相场法数值模拟[J]. 中国有色金属学报, 2005, 15(7): 1026-1032.
ZHU Yao-chan, YANG Gen-cang, WANG Jin-cheng, et al. Multi-phase field simulation of unidirectional solidification for binary eutectic alloy[J]. The Chinese Journal of Nonferrous Metals, 2005, 15(7): 1026-1032.
[26]Kim S G, Kim W T, Suzuki T, et al. Phase-field modeling of eutectic solidification[J]. J Crystal Growth, 2004, 261: 135-158.
[27]Drolet F, Elder K R, Grant M, et al. Phase-field modeling of eutectic growth[J]. Physical Review E , 2000, 61: 6705-6720.
[28]Plapp M, Karma A. Eutectic colony formation: A phase-field study[J]. Physical Review E, 2002, 66: 061608.
[29]Plapp M, Karma A. Eutectic colony formation: A stability analysis[J]. Physical Review E , 1999, 60, 6865-6889.
[30]Akamatsu S, Plapp M, Fairvre G, et al. Pattern stability and tri-junction motion in eutectic solidification[J]. Physical review E, 2002, 66: R030501.
[31]Akamatsu S, Sabine B R, Faivre G. Experimental evidence for a zigzag bifurcation in bulk lamellar eutectic growth[J]. Physical Review Letters, 2004, 93: 175701.
[32]Magnin P, Trivedi R. Eutectic growth: A modification of the Jackson and Hunt theory[J]. Acta Metall Mater, 1991, 39(4): 453-467.
[33]Chen Y J, Davis S H. Instability of triple juctions in lamellar eutectic growth[J]. Acta Materialia, 2001, 49: 1363-1372.
[34]Chen Y J, Davis S H. Dynamics and instability of triple junctions of solidifying eutectics: Flow-modified morphologies[J]. Acta Materialia, 2002, 50: 2269-2284.
[35]SU Yun-peng, LIN Xin, WANG Meng, et la. Lamellar structures in laser surface remelted Zn-Cu peritectic alloy under ultra-high temperature gradient[J]. Scripta Mater, 2004, 51(5): 397-403.
[36]SU Yun-peng, LIN Xin, WANG Meng, et al. Researches on lamellar structures in the unidirectional solidified Zn-2 wt.% Cu peritectic alloy[J]. Materials Letters, 2004, 58(21): 2670-2674.
[37]王猛, 林鑫, 苏云鹏, 等. Zn-Cu包晶合金定向凝固组织演化(Ⅰ): 实验现象及分析[J]. 金属学报, 2003, 39(8): 831-837.
WANG Meng, LIN Xin, SU Yun-peng, et al. Microstructure evolution in unidirectionally solidified Zn-Cu peritectic alloy (Ⅰ): Experiment and analysis[J]. Acta Metallurgica Sinica, 2003, 39(8): 831-837.
[38]王猛, 林鑫, 苏云鹏, 等. Zn-Cu包晶合金定向凝固组织演化(Ⅱ): 相选择的改进分析[J]. 金属学报, 2003, 39(8): 838-842.
WANG Meng, LIN Xin, SU Yun-peng, et al. Microstructure evolution in unidirectionally solidified Zn-Cu peritectic alloy (Ⅱ): Modification on the analysis[J]. Acta Metallurgica Sinica, 2003; 39(8): 838-842.
[39]LIU Yong-chang, LAN Feng, YANG Gen-chang, et al. Microstructural evolution of rapidly solidified Ti-Al peritectic alloy[J]. J Crystal Growth, 2004, 271: 313-318.
[40]LIU Yong-chang. Lamellar spacing and mechanical property of undercooled Ti-45Al-2Cr- 2Nb alloy[J]. Materials Letters, 2003, 57(15): 2262-2266.
[41]Dobler S, Lo T S, Plapp M, et al. Peritectic coupled growth[J]. Acta Materialia, 2004, 52: 2795-2808.
[42]Lo T S, Dobler S, Plapp M, et al. Two-phase microstructure selection in peritectic solidification: from island banding to coupled growth[J]. Acta Materialia, 2003, 51(3): 599-611.
[43]Vandyoussefi M, Kerr H W, Kurz W. Two-phase growth in peritectic Fe-Ni alloys[J]. Acta Materialia, 2000, 48(9): 2297-2306.
[44]Vandyoussefi M, Kerr H W, Kurz W. Directional solidification and δ/γ solid state transformation in Fe-3%Ni alloy[J]. Acta Materialia, 1997, 45(10): 4093-4105.
[45]Lee J H, Verhoeven J D. Peritectic formation in the Ni-Al system[J]. J Crystal Growth, 1994, 144: 353-366.
[46]傅恒志, 苏彦庆, 郭景杰, 等. 高温金属间化合物的定向凝固特性[J]. 金属学报, 2002, 38(11): 1127-1132.
FU Heng-zhi, SU Yan-qing, GUO Jing-jie, et al. The solidification behavior of high temperature intermetallics[J]. Acta Metallurgica Sinica, 2002, 38(11): 1127-1132.
[47]Ma D, Jie W Q, Li Y, et al. Effect of weak convection on lamellar spacing of eutectics[J]. Acta Materialia, 1998, 46(9): 3203-3210.
[48]Quenisset J M, Naslain R. Effect of forced convection on eutectic growth[J]. J Crystal Growth, 1981, 54: 465-474.
[49]Wang W M, Liu J M, Chen X Y, et al. Eutectic patterns with weak convection in binary systems[J]. J Crystal Growth, 2002, 240: 313-320.
[50]Kassner K, Misbah C. Parity breaking in eutectic growth[J]. Physical Review Letters, 1990, 65(12): 1458-1461.
[51]Seetharaman V, Trivedi R. Eutectic growth: Selection of interlamellar spacings[J]. Metal Mater Trans A, 1988, 19: 2955-2964.
[52]Kassner K, Misbah C. Similarity laws in eutectic growth[J]. Physical Review Letters, 1991, 66(4): 445-448.
[53]Kassner K, Misbah C. Growth of lamellar eutectic structures: The axisymmetric state[J]. Physical Review A, 1991, 44(10): 6513-6532.
[54]Trivedi R, Magnin P, Kurz W. Theory of eutectic growth under rapid solidification conditions[J]. Acta Metall Mater, 1987, 35(4): 971-980.
[55]Kurz W, Trivedi R. Eutectic growth under rapid solidification conditions[J]. Metal Mater Trans A, 1991, 22: 3051-3057.
[56]姚文静, 魏炳波. 落管中Co-Sn共晶合金的快速凝固[J]. 自然科学进展, 2003, 13(9): 964-969.
YAO Wen-jing, WEI Bing-bo. Rapid solidification of Co-Sn eutectic alloy in drop tube[J]. Progress in Nature Science, 2003; 13(9): 964-969.
[57]朱定一, 杨晓华, 魏炳波. Cu-Cr二元过共晶合金的深过冷及快速凝固[J].中国有色金属学报, 2002, 12(5): 891-896.
ZHU Ding-yi, YANG Xiao-hua, WEI Bing-bo. Rapid solidification microstructures of Cu-Cr binary hypereutectic alloy at deep undercooling[J].The Chinese Journal of Nonferrous Metals, 2002, 12(5): 891-896.
[58]Yao W J, Wang N, Wei B. Containerless rapid solidification of highly undercooled Co-Si eutectic alloys[J]. Mater Sci Eng A, 2003, 344: 10-19.
[59]Liu X R, Cao C D, Wei B. Microstructure evolution and solidification kinetics of undercooled Co-Ge eutectic alloys[J]. Scripta Mater, 2002, 46: 13-18.
[60]Karma A. Beyond steady state lamellar eutectic growth[J]. Physical Review Letters, 1987, 59(1): 71-74.
[61]Kassner K, Valance A, Misbah C, et al. New broken-parity state and a transition to anomalous lamellar in eutectic growth[J]. Physical Review E, 1993, 48(2): 1091-1105.
[62]Valance A, Misbah C, Temkin D, et al. Analytic theory for parity breaking in lamellar eutectic growth[J]. Physical Review E, 1993, 48(3): 1924-1941.
[63]Kirkaldy J S. Predicting the patterns in lamellar growth[J]. Physical Review B, 1984, 30(12): 6889-6895.
[64]Ginibre M, Akamatsu S, Faivre G. Experimental determination of the stability diagram of a lamellar eutectic growth front[J]. Physical Review E, 1997, 56(3): 780-796.
[65]Kassner K, Misbah C. Coupling between crystalline anisotropy and spontaneous parity breaking in lamellar eutectic growth[J]. Physical Review A, 1992, 45: 7372-7384.
[66]Elder K R, Gunton J D, Grant M. Nonisothermal eutectic crystallization[J]. Physical Review E, 1996, 54(6): 6476-6484.
[67]Langer J S. Eutectic solidification and marginal stability[J]. Physical Review Letters, 1980, 44(15): 1023-1026.
[68]Datye V, Langer J S. Stability of thin eutectic growth[J]. Physical Review B, 1981, 24(8): 4155-4169.
[69]Ginibre M, Akamatsu S, Faivre G. Experimental determination of the stability diagram of a lamellar eutectic growth front[J]. Physical Review E, 1997, 56(1): 780-796.
[70]Hermann R, Loser W. Extension of the primary solidification region of Nd2Fe14B by levitation of undercooled melts[J]. Journal of Applied Physics, 83(11): 6399-6401.
[71]Tent B A, Qu D, Shi D L, et al. Angle dependence of magnetization in a single-domain YBa2Cu3Ox sphere[J]. Physical Review B, 58(17): 11761-11767.
[72]Boettinger W J, Coriell S R, Greer A L, et al. Solidification microstructures: Recent developments, future directions[J]. Acta Materialia, 2000, 48: 43-70.
[73]Akamatsu S, Moulinet S, Faivre G. The formation of lamellar-eutectic grains in thin samples[J]. Metal Mater Trans A, 2001, 32A: 2039-2048.
(编辑陈爱华)
基金项目: 国家自然科学基金资助项目(50395102, 50271020); 新世纪优秀人才资助计划资助项目(2005-0350)
收稿日期: 2006-01-09; 修订日期: 2006-04-19
通讯作者: 苏彦庆, 教授; 电话: 0451-86417395; E-mail: suyq@hit.edu.cn

