闭孔粉煤灰泡沫铝的应变速率敏感性
来源期刊:中国有色金属学报(英文版)2013年第4期
论文作者:Manmohan DASS GOEL VASANT A. MATSAGAR Anil K. GUPTA Steffen MARBURG
文章页码:1080 - 1089
关键词:高应变速率;泡沫金属; 应变速率敏感性;数值模拟;分离式Hopkinson压杆
Key words:high strain rate; metal foam; strain rate sensitivity; numerical simulation; split Hopkinson pressure bar
摘 要:随着金属泡沫在工程应用中的增加,对它们在不同应变速率下的动态行为进行研究是有必要的。采用熔体发泡法制备闭孔粉煤灰泡沫铝,并对其在应变速率从700 s-1增加到1950 s-1时的应力—应变行为进行研究。使用商用有限元软件Abaqus/Explicit对分离式霍普金森压杆(SHPB)的数学模型进行模拟。实验和模拟结果证实了数学模型是可用的。研究了应变速率对抗压强度和能量吸收的影响,得到了多种应变率下的应力—应变曲线。结果表明,闭孔粉煤灰泡沫铝对应变速率是敏感的。
Abstract: With the increasing use of metal foams in various engineering applications, investigation of their dynamic behaviour under varying strain rate is necessary. Closed cell aluminium fly ash foam developed through liquid metallurgy route was investigated for its stress—strain behaviour at different strain rates ranging from 700 s-1 to 1950 s-1. The numerical model of split Hopkinson pressure bar (SHPB) was simulated using commercially available finite element code Abaqus/Explicit. Validation of numerical simulation was carried out using available experimental and numerical results. Full scale stress—strain curves were developed for various strain rates to study the effect of strain rate on compressive strength and energy absorption. The results showed that the closed cell aluminium fly ash foam is sensitive to strain rate.
Trans. Nonferrous Met. Soc. China 23(2013) 1080-1089
Manmohan DASS GOEL1, Vasant A. MATSAGAR2, Anil K. GUPTA1, Steffen MARBURG3
1. CSIR-Advanced Materials and Processes Research Institute (AMPRI), Council of Scientific and Industrial Research (CSIR), Bhopal-462 064, India;
2. Department of Civil Engineering, Indian Institute of Technology (IIT) Delhi, New Delhi-110 016, India;
3. Department of Aerospace Engineering, University of German Armed Forces, Neubiberg - 85577, Munich, Germany
Received 9 May 2012; accepted 19 November 2012
Abstract: With the increasing use of metal foams in various engineering applications, investigation of their dynamic behaviour under varying strain rate is necessary. Closed cell aluminium fly ash foam developed through liquid metallurgy route was investigated for its stress—strain behaviour at different strain rates ranging from 700 s-1 to 1950 s-1. The numerical model of split Hopkinson pressure bar (SHPB) was simulated using commercially available finite element code Abaqus/Explicit. Validation of numerical simulation was carried out using available experimental and numerical results. Full scale stress—strain curves were developed for various strain rates to study the effect of strain rate on compressive strength and energy absorption. The results showed that the closed cell aluminium fly ash foam is sensitive to strain rate.
Key words: high strain rate; metal foam; strain rate sensitivity; numerical simulation; split Hopkinson pressure bar
1 Introduction
Metal foams had shown many interesting properties for their applications in blast resistance and crashworthiness [1]. To use metal foam efficiently in these applications, their characterization in terms of dynamic properties is of foremost importance. To investigate the mechanical behaviour of metal foams at higher strain rates, split Hopkinson pressure bar (SHPB) test is required. Several researchers in the past have experimentally investigated the deformation behaviour of aluminium foams at different strain rates ranging from quasi-static to high strain rates (about 5000 s-1) and reported diverse results about the strain rate sensitivity of these foams [2-14]. The recent applications of lightweight materials in various advanced fields served as motivation for the development of numerical models. These models have mandated the need for realistic constitutive data at high strain rates. These data are required as inputs for computational design models. If accurate numerical results can be obtained from the computational models and high strain rate test data, the need to conduct expensive tests may be effectively reduced. This not only translates into significant cost savings, but also will allow the manufacturer to make minor adjustments in their designs in a more timely and efficient manner.
KENNY [2], LANKFORD and DANNEMANN [3], DESHPANDE and FLECK [4] and RUAN et al [8] studied the compressive deformation of metal foams over wide range of strain rates (0.001 s-1 to 5000 s-1) and concluded that the compressive strength of the foam is independent of the strain rate. However, PAUL and RAMAMURTY [5], KANAHASHI et al [6], DANNEMANN and LANKFORD [7], MUKAI et al [9], CAO et al [10], ELNASRI et al [12] and EDWIN RAJ et al [13] studied aluminium foams at varying strain rates and concluded that the plastic strength increases with the increase in strain rate. WANG et al [14] developed the elasto-plastic constitutive model of aluminium alloy foam subjected to impact loading.
During SHPB tests, several factors, such as longitudinal wave dispersion, impedance mismatch between bar and specimen materials, instrumentation, influence the accuracy of the results. In the past several researchers studied these problems and presented various solutions [2-14]. Recent advance in this area included numerical simulation technique to determine the stress—strain curve numerically for particular strain rates and then it was verified experimentally to determine the source of errors. Based on the review of the past literature, it is observed that consensus on the dynamic behaviour of aluminium foams with strain rate sensitivity is absent. Different schools of thought exist on the past investigations about the strain rate sensitivity of aluminium foams. In fact, the understanding on the influence of strain rate on the compressive deformation behaviour of aluminium foams is yet to be fully developed. With the existence of many contradictory opinions about the strain rate sensitivity of the aluminium foams, it becomes necessary to carry out the strain rate characterization of the foam materials before actually using these in dynamic applications. This is carried out using SHPB test, which is commonly used for characterization of materials at high strain rates and to generate the stress—strain curve of the foam materials at high strain rates.
Hence, in the present investigation, the closed cell aluminium fly ash foam made through liquid metallurgy route at Advanced Materials and Processes Research Institute (AMPRI), Council of Scientific and Industrial Research (CSIR), Bhopal, India, is studied using numerical simulation for strain rate sensitivity. Validation of numerical simulation is first carried out using available experimental results followed by numerical modelling of complete SHPB test setup using Abaqus/ Explicit [15]. This study is carried out with an aim of understanding the simulation technique for SHPB test setup and thereby reducing the experimental work and efforts especially for foam materials. By the numerical simulation a large number of studies can be carried out; otherwise, it would be difficult to study through experimentation involving large amount of time, resource and tediousness. Hence, the present investigation is carried out with objective to develop a simple finite element model of SHPB test and to simulate dynamic compression response based on quasi-static test to measure the mechanical response at high strain rates, to study the dynamic compression properties, i.e. compressive strength and energy absorption at higher strain rates, to develop full scale stress-strain curves at different strain rates and to study the strain rate sensitivity of closed cell aluminium fly ash foam.
2 Experimental
In the present investigation, the closed cell aluminium fly ash foams were prepared using ultra fine fly ash particle as thickening agent and calcium hydride (CaH2) as foaming agent through liquid metallurgy route. Fly ash particles in the size range of 2-10 μm of about 5% in mass fraction were used. CaH2 powder (having size range of 20-30 μm) of 0.60% was used as foaming agent. An A2014 Al alloy was used as the virgin alloy (composition: 90.5%-93.7% Al, 0.5%-1.2% Si, 0.7% Fe, 3.9%-5.0% Cu, 0.4%-1.2% Mn, 0.2%-0.8% Mg, 0.1% Cr, 0.25% Zi, 0.1% Ti, 0.15% others). Aluminium fly ash foams were developed through liquid metallurgy route which involved the following steps: 1) melting of the alloy, 2) mixing of preheated fly ash particles in the alloy melt, 3) dispersion of calcium hydride (CaH2) particles in the melt, 4) allowing the melt for a short duration in the foaming temperature for completion of foaming, 5) immediate cooling of the crucible in which the foaming was carried out through forced air and 6) ejection of foam from the crucibles after cooling [16]. The foaming temperature was varied in the range of 675-695 °C with an interval of 5 °C to achieve different relative densities (RD) of foams. Hydrogen gas bubbles were entrapped in the melt to cause foaming of the melt. The addition of fly ash particles increased the viscosity of the melt and acted as an excellent thickening agent because the fly ash particles are chemically inert with aluminium melt and are physically and chemically stable in the aluminium melt. The diameter of the cell was measured according to the method prescribed by ASTM for the measurement of grain diameter in polycrystalline multiphase materials [17]. The cell size (cell diameters) of the synthesized foam varied in the range of 1.7-3.2 mm with an average cell size of 1.9 mm. The cell sizes of foams changed with their relative densities. Figure 1 shows a bulk aluminium fly ash foam sample and its microstructure.
The cell size, cell wall thickness and relative density as a function of temperature in the closed cell aluminium fly ash foam used in the present investigation are shown in Table 1. The average pore diameter was determined by calculating the pore diameter at different locations along the foaming direction and also along the transverse direction [1]. It can be observed that the cell size increased with increase in temperature, wherein the cell wall thickness decreased with increase in temperature. The relative density, which is defined as the ratio of density of foam to the density of dense material, is a strong function of temperature. It is obvious from the variation of cell size and cell wall thickness that the relative density would decrease with the increase in temperature.
Quasi-static compression tests of the developed foam were conducted in BiSS universal testing machine at a strain rate of 0.001 s-1 [16]. For compression testing, specimens were cut off from the fabricated foam with average dimensions of 40 mm×45 mm in cross-section and 55 mm in height. The surface of the specimens was polished mechanically prior to testing and was lubricated with thin molybdenum sulphide coating so as to reduce the friction between the specimen surface and the compression test platens. The load—displacement data was recorded during the testing and converted to stress—strain curves by standard method.

Fig. 1 Representative closed cell aluminium fly ash bulk foam
Table 1 Cell size, cell wall thickness and relative densities of closed cell aluminium fly ash composite foams


Fig. 2 Quasi-static compressive stress—strain curve for closed cell aluminium fly ash foam
A compressive stress—strain curve of closed cell aluminium fly ash foam is shown in Fig. 2. To avoid clustering, only one stress—strain curves for relative density, 0.107, is reported in Fig. 2. The stress—strain curves clearly depict five regimes: 1) a linear portion at the initial stage indicating elastic portion, 2) just after yielding there is a small flat region, 3) after the flat regime, sharp drop of stress with strain and then again increase with increase in strain indicating a well-defined yield point, 4) a plateau region where the plastic deformation and compaction of the foam take place at almost constant stress level and 5) densification region beyond the densification strain where the foam starts densifying after compaction and plastic deformation. It is noted that the stress in the plateau region follows a zig-zag nature which may be due to the localized cell deformation, crushing and compaction propagated layer by layer. Herein, plateau stress was considered the average stress in the plateau region and the densification strain was considered to be the strain corresponding to the intersection of tangents drawn on the densified and the plateau regions. This quasi-static compression curve is helpful for computing the various parameters of constitutive model used in the present study. Table 2 shows the properties deduced from this curve and the same ones are used in the present investigation. These include elastic modulus E, yield stress σy at 0.2% of the total strain, compressive strength σc, plateau stress σp1 and densification strain εd.
Table 2 Mechanical properties of closed cell aluminium fly ash foam

3 SHPB test assembly

Fig. 3 Schematic of SHPB apparatus for compression testing of foam (a) and wave propagation (x-t) diagram (b)
SHPB test setup was developed to study the dynamic behaviour of materials at high strain rates. It consists of a striker, incident and transmitter bar. The striker bar impacts the incident bar and generates a stress pulse which travels along the transmitted bar as well as reflects at interfaces. If C0 is the wave speed within the bar, Ls is the length/thickness of foam specimen, the axial displacement u1 of the incident bar and specimen interface is computed from the incident (εI) and the reflected (εR) strain records as (Fig. 3)
 (1)
(1)
Similarly, the displacement u2 of the specimen and transmitter bar interface is obtained from the transmitted strain (εT) as
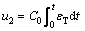 (2)
(2)
The compressive strain (εC) in the specimen is computed using the following relation,
 (3)
(3)
The forces at the incident bar and specimen interface, F1, and at the transmitter bar and specimen interface, F2, are computed as follows:
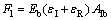 (4)
(4)
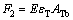 (5)
(5)
where AIb and ATb are the cross-sectional areas of the incident and transmitter bar respectively and Eb is the elastic modulus of the bar. At the state of dynamic equilibrium of specimen, there is
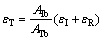 (6)
(6)
Hence, substituting Eq. (6) into Eq. (3) and rearranging the terms, we get
 (7)
(7)
The strain rate in the specimen can be computed by evaluating the slope of the linear portion of the stain time history [18]. These pulses are collected by the proper instrumentation techniques using strain gauges attached at appropriate levels all along incident and transmitter bars [19]. These include measuring incident strain εI(t), the transmitted strain εT(t) and the reflected strain εR(t). The stress—strain response and strain rates were computed using the following standard relations developed based on simplified one-dimensional wave propagation theory [19],
 (8)
(8)
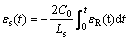 (9)
(9)
 (10)
(10)
where As and Ab are the cross-sectional areas of the specimen and bar, respectively; εs(l) is the strain rate; t is the time; σs and εs are stress and strain induced in the specimen, respectively. Figure 3 shows the schematic of test assembly, and the properties of SHPB bars, i.e. density r, elastic modulus E, Poisson ratio ν, and elastic wave speed  used in the present investigation are summarised in Table 3. All the components, i.e. striker, incident and transmitter bars, were made of PMMA (polymethylmethacrylate) and the properties reported by
used in the present investigation are summarised in Table 3. All the components, i.e. striker, incident and transmitter bars, were made of PMMA (polymethylmethacrylate) and the properties reported by  et al [20] were used in the present numerical investigation. Low impedance material was used for modelling the striker, incident and transmitter bars for enhanced accuracy particularly for the case of metal foams wherein conventional steel striker, incident and transmitter bars do not yield good results [18,20]. By following the above strategy the data were produced and subsequently reduced.
et al [20] were used in the present numerical investigation. Low impedance material was used for modelling the striker, incident and transmitter bars for enhanced accuracy particularly for the case of metal foams wherein conventional steel striker, incident and transmitter bars do not yield good results [18,20]. By following the above strategy the data were produced and subsequently reduced.
Table 3 Properties for SHPB components, i.e. striker, incident and transmitter bars

4 Numerical modelling/FEM simulation
In the present investigation, finite element code Abaqus/Explicit was used for modelling the foam under dynamic compression in accordance with the SHPB test. Crushable foam model available in Abaqus material model library was used for modelling the closed cell aluminium fly ash foam [15]. In the present investigation, foam hardening is considered to be isotropic, which is a true behaviour of the fly ash foam, observed during quasi-static compression test. This model considers a yield surface with an elliptical dependence of deviatoric stress on pressure stress in the meridional plane [21]. Further, it assumes symmetric behaviour in tension and compression and the evolution of yield surface is governed by an equivalent plastic strain, which has contributions from both the volumetric plastic strain and the deviatoric plastic strain. The elastic behaviour inside yield surface is represented with linear elastic model as
 (11)
(11)
where σ, Del and eel represent the second order stress, the fourth order elasticity tensor and elastic strain tensor, respectively. The yield surface and the flow potential are defined in terms of the pressure stress respectively as [21]
 (12)
(12)
 (13)
(13)
where F and G are represented as an ellipse in the p-q stress plane with α and β representing the shape of the yield ellipse and ellipse for the flow potential respectively; p0 is the centre of yield ellipse; B is the length of vertical q-axis of the yield surface. The flow potential is an ellipse centred in the origin. Further, the ellipse for the flow potential is related to the plastic Poisson ratio, νp as [21]
 (14)
(14)
In the present investigation, νp is assumed to be zero based on the quasi-static compression test of the foam. The various parameters required for above model were obtained from the quasi-static stress—strain curve (Fig. 1 and Table 2).
4.1 FE model of SHPB
In the present investigation, the striker has a length of 330 mm and diameter of 22 mm; the incident and transmitter bar have length of 1000 mm each and diameter of 22 mm. The specimen size considered in the present investigation was 14 mm in diameter and 7 mm in length taking into account the effect of pore size on the specimen [1,4,10,13,18,20]. The thin sample was used in the present investigation to facilitate the stress equilibrium at initial stage of the SHPB test [18]. The striker, incident and transmitter bars were modelled as elastic bars with the material properties reported in Table 3.

Fig. 4 3D mesh for SHPB test
Three dimensional solid eight node brick elements with reduced integration and hour glass control designated as C3D8R in Abaqus theory manual were used for modelling the assembly of striker, incident, transmitter bars and the specimen. The C3D8R elements take into account the large mesh distortion without affecting the results due to volumetric locking which is a common problem in large deformation analysis. Figure 4 shows the 3D mesh for the bars and foam specimen used in the present investigation. The foam specimen was meshed using a global seed of 0.003 and bars were meshed using a global seed of 0.05 considering accurate enough for obtaining the strain profile. The boundary conditions were applied to the bars and specimen such that movement in the direction of striker bar was allowed to simulate the one-dimensional wave propagation which is the basis of the SHPB tests. A general contact algorithm was used to define contact between the bars and specimen in the SHPB test. A central difference scheme was used to integrate the equations of motion explicitly through time. The method is conditionally stable for time increments (Dt) that are smaller than Courant time limit, △t≤l/c, where l is the smallest element dimension and c is the speed of sound wave in medium in which it travels. Also, the artificial bulk viscosity was activated to properly represent the propagation of the induced compressive stress wave by employing quadratic and linear functions of volumetric strain rates with values of 1.2 and 0.06, respectively. Gauges in the form of reference points were placed at several locations along the specimen length and bars in order to collect the data of incident, reflected and transmitted waves. The contact surfaces between the incident bar, specimen and transmitter bar are defined to be frictionless. In the next section, validation of the finite element based numerical model was presented.
4.2 Validation of numerical approach
The finite element approach used in the present simulation is similar to that reported by  et al [20] and the validation of the present finite element (FE) approach was presented using the results reported by them. HASAN et al [22] presented experimental and numerical results for stress—strain behaviour of normal strength concrete subjected to high strain rate using SHPB. They compared the results of experimental test and numerical simulation at strain rates of 350 s-1, 500 s-1 and 700 s-1. Hence, for improved confidence in the FE modelling, the second validation was also carried out using the results reported by them.
et al [20] and the validation of the present finite element (FE) approach was presented using the results reported by them. HASAN et al [22] presented experimental and numerical results for stress—strain behaviour of normal strength concrete subjected to high strain rate using SHPB. They compared the results of experimental test and numerical simulation at strain rates of 350 s-1, 500 s-1 and 700 s-1. Hence, for improved confidence in the FE modelling, the second validation was also carried out using the results reported by them.
4.2.1 AlporasTM foam
 et al [20] reported the numerical simulation of AlporasTM foam using Abaqus. In the present investigation, PMMA bars were used for modelling the SHPB test and its validation. In their SHPB test setup model, striker had a length of 330 mm and diameter of 22 mm; the incident and transmitter bars had length of 1000 mm each and a diameter of 22 mm. The specimen size considered in their investigation was 14 mm in diameter and 7 mm in length. The striker, incident and transmitter bars were modelled as elastic bars with the material properties reported by
et al [20] reported the numerical simulation of AlporasTM foam using Abaqus. In the present investigation, PMMA bars were used for modelling the SHPB test and its validation. In their SHPB test setup model, striker had a length of 330 mm and diameter of 22 mm; the incident and transmitter bars had length of 1000 mm each and a diameter of 22 mm. The specimen size considered in their investigation was 14 mm in diameter and 7 mm in length. The striker, incident and transmitter bars were modelled as elastic bars with the material properties reported by  et al [20]. Three dimensional solid eight node brick elements with reduced integration and hour glass (C3D8R) were used for modelling the assembly of striker, incident, transmitter bars and specimen [15]. The foam specimen had 320 elements in cross section and 7 elements along the length, and the bars had 96 elements in their cross section and 80 elements along the length. Figure 5 shows the results of
et al [20]. Three dimensional solid eight node brick elements with reduced integration and hour glass (C3D8R) were used for modelling the assembly of striker, incident, transmitter bars and specimen [15]. The foam specimen had 320 elements in cross section and 7 elements along the length, and the bars had 96 elements in their cross section and 80 elements along the length. Figure 5 shows the results of  et al and the results obtained using the present FE simulation by the same approach. It is observed that both the results are in close agreement.
et al and the results obtained using the present FE simulation by the same approach. It is observed that both the results are in close agreement.
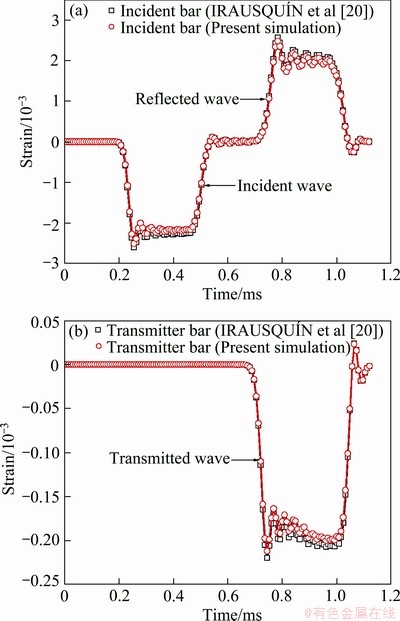
Fig. 5 Validation of present FE simulation with  et al [20] in terms of incident, reflected and transmitted strain histories
et al [20] in terms of incident, reflected and transmitted strain histories
4.2.2 HASAN et al’s results
HASAN et al [22] reported the experimental and numerical simulation of concrete using SHPB test. In their study, striker had a length of 1000 mm and diameter of 60 mm; whereas, the incident and transmitter bars had length of 4500 mm each and diameter of 60 mm. The specimen size of the concrete (ultimate compressive strength of 30 MPa) was 36 mm in diameter and 36 mm in length. The striker, incident and transmitter bars were modelled as elastic bars with the material properties, loading and boundary condition as reported by them. Figure 6 shows the results of HASAN et al [22] and the results obtained using the present FE simulation. It is observed that both the results are in close agreement, validating the present FE simulation.

Fig. 6 Validation of present FE simulation with HASAN et al’s result for concrete at strain rate of 500 s-1

Fig. 7 Strain—time history at incident bar in terms of incident and reflected strain waves for different striker velocities

Fig. 8 Strain—time history at transmitter bar in terms of transmitted strain wave for different striker velocities
5 Results and discussion
Figures 7 and 8 show the strain—time histories at incident and transmitted bar obtained by applying different velocities of striker in the present FE
simulation. These figures show strain—time histories of the incident, reflected and transmitted strain waves for striker velocities vs of 6, 10 and 15 m/s, respectively. The data from these figures were used for computation of stress—strain curves of foam corresponding to strain rates generated by these striker velocities. Figure 9 shows the strain rate—time history computed using Eq. (8) for different striker velocities. It is clear from this figure that there exists strong dependency between striker velocity and strain rate. It is observed from this figure that the strain rates corresponding to 6, 10 and 15 m/s of striker velocity are 700, 1300 and 1950 s-1, respectively. The mean values of the strain rates were used for computation purpose.

Fig. 9 Strain rates achieved by varying striker velocities for dynamic compression of closed cell fly ash aluminium composite foam
Figure 10 shows the compressive stress—strain relationship of closed cell aluminium fly ash foam at different strain rates computed using Eqs. (9) and (10) along with the quasi-static compression curve for foam with relative density of 0.107. The computed stress—strain curve exhibits higher plateau stress in comparison with the quasi-static compression curve (which is zigzag in nature), indicating the strain rate sensitivity of the foam considered in the present investigation obtained by numerical simulation. Further, it can be observed that due to the presence of rate sensitivity, elastic phase of the stress—strain curve shifts upwards, indicating higher elastic modulus. The elastic responses under static and dynamic conditions also show differences. The plateau stress shows a nonlinear increasing trend with the increase of strain rates. The dynamic response of the foam has two distinct regions: 1) an initial linear elastic region followed by peak yield stress and 2) a monotonically decreasing stress region with increasing strain which again starts densifying after a particular value of strain, indicating the typical characteristics of such low density foam. This behaviour was even observed in the quasi-static tests wherein the foam started densifying after the densification strain was reached (Fig. 2). It was observed that the plateau strengths of the closed cell aluminium fly ash foam at 700, 1300 and 1950 s-1 strain rates were 2.40, 2.60, and 2.70 MPa, respectively. It was observed that the relative increase in the plateau strengths from its quasi-static values lies in order 8%, as shown in Fig. 11. Further, it was observed that the dynamic loading clearly suppressed the distinct zigzag behaviour seen in quasi-static cases after the initial peak stress and instead of this zigzag nature, so a smooth curve was obtained as seen in Fig. 10.
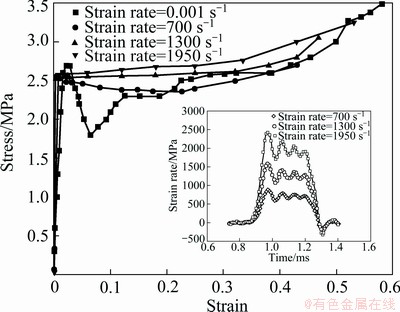
Fig. 10 Compressive stress—strain curves obtained using numerical simulation at different strain rates along with quasi-static experimental compression curve
The significant aspect of such foam is in structural applications for energy absorption. In order to study the effect on energy absorption, a comparison of energy absorbed per unit volume under dynamic loading conditions with that of quasi-static condition was carried out. The energy absorption (Eabs) per unit volume of the present closed cell aluminium fly ash foam was computed by calculating the area under stress—strain curve up to densification strain (45% here) as
 (15)
(15)
where σ is the stress and ed is the densification strain. The Eabs per unit volume of the present closed cell aluminium fly ash foam along with compressive strength and plateau strength are reported in Fig. 11. It can be observed that the energy absorption of the present foam is higher under dynamic loading which is due to higher compressive and plateau strength of the foam. Moreover, energy absorption increased by up to 35% for the strain rates under dynamic loading. Higher energy absorption under dynamic condition is attributed to relatively higher yield stress or flow stress compared with that in quasi-static condition and smooth transition between yielding and plastic region. Further, it can be observed from Fig. 11 that the yield strength and plateau strength of foam at quasi-static condition are relatively high compared with the strain rate of 700 s-1, which may be attributed to the fact that in quasi-static condition the stress—strain curve is zigzag in nature due to its gradual crushing and collapsing of pore spaces; in dynamic condition, there exists a smooth transition. However, at higher strain rates (i.e. 1300 and 1950 s-1) there exists a distinct variation observed from Fig. 11. Moreover, energy absorption increases considerably at higher strain rates.
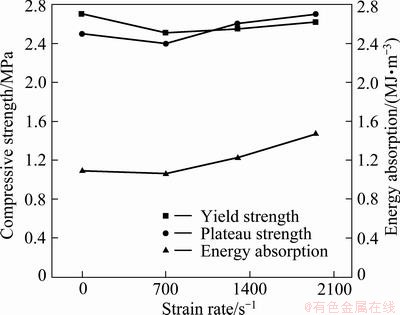
Fig. 11 Variation of dynamic properties in comparison with quasi-static values
6 Summary and conclusions
Numerical analysis was carried out in the present investigation with objective 1) to develop a simple finite element model of SHPB test and to simulate dynamic compression response based on quasi-static test to measure the mechanical response at high strain rates, 2) to study the dynamic compression properties, i.e. compressive strength and energy absorption at higher strain rates, 3) to develop full scale stress-strain curves at different strain rates and 4) to study the strain rate sensitivity of closed cell aluminium fly ash foam. First of all, validation of the present FE simulation was carried out by comparing the results with the available results. Closed cell aluminium fly ash foam was analyzed with three different striker velocities leading to three different strain rates, i.e. 700, 1300 and 1950 s-1. The results indicated that the plateau stress of closed cell aluminium fly ash foam considered in the present investigation showed strain rate sensitivity when moving from quasi-static (<1 s-1) to high strain rates (1950 s-1) for a foam with relative density of 0.107. Moreover, the strain rates influence not only the plateau stress but also the elastic region of the stress—strain curve. Plateau stress was observed to increase nonlinearly with the increase in strain rates. Compressive strength and energy absorption were observed to increase under the influence of strain rates based on the developed full scale stress—strain curves. Moreover, it was confirmed that numerical simulation can be utilised for investigating the foams under varying strain rates using the numerical SHPB setup as these simulations work well and provide agreeable results. Finally, this study showed the effectiveness of numerical simulation in the investigation of the effect of strain rates on low impedance materials such as closed cell aluminium fly ash foam used in the present investigation.
Acknowledgement
The doctoral scholarship received to the lead author from German Academic Exchange Service, i.e. DAAD (Deutscher Akademischer Austausch Dienst) in completing the reported investigation is gratefully acknowledged.
References
[1] ASHBY M F, GIBSON L, EVANS A. Metal foams—A design guide [M]. Boston: Butterworth-Heinemann, 2000.
[2] KENNY L D. Mechanical properties of particle stabilised aluminium foam [J]. Materials Science Forum, 1996, 217-222: 1883-1890.
[3] LANKFORD J, DANNEMANN K A. Strain rate effects in porous materials [J]. Proceedings of Symposium of Material Research Society, 1998, 521: 103-108.
[4] DESHPANDE V S, FLECK N A. High strain rate compressive behaviour of aluminium alloy foams [J]. International Journal of Impact Engineering, 2000, 24: 277-298.
[5] PAUL A, RAMAMURTY U. Strain rate sensitivity of a closed-cell aluminium foam [J]. Material Science and Engineering A, 2000, 281: 1-7.
[6] KANAHASHI H, MUKAI T, YAMADA Y, SHIMOJIMA K, MABUCHI M, NIEH T G, HIGASHI H. Dynamic compression of an ultra-low density aluminium foam [J]. Material Science and Engineering A, 2000, 280: 349-353.
[7] DANNEMANN K A, LANKFORD J. High strain rate compression of closed-cell aluminium foams [J]. Material Science and Engineering A, 2000, 293: 157-164.
[8] RUAN D, LU G, CHEN F L, SIORES E. Compressive behaviour of aluminium foams at low and medium strain rates [J]. Composite Structures, 2002, 57: 331-336.
[9] MUKAI T, MIYOSHI T, NAKANO S, SOMEKAWA H, HIGASHI K. Compressive response of a closed-cell aluminium foam at high strain rate [J]. Scripta Materialia, 2006, 54(4): 533-537.
[10] CAO Xiao-qing, WANG Zhi-hua, MA Hong-wei, ZHAO Long-mao, YANG Gui-tong. Effects of cell size on compressive properties of aluminium foam [J]. Transactions of Nonferrous Metals Society of China, 2006, 16(2): 351-356.
[11] PERONI M, PERONI L, AVALLE M. High strain-rate compression test on metallic foam using a multiple pulse SHPB apparatus [J]. Journal de Physique IV, 2006, 134: 609-616.
[12] ELNASRI I, PATTOFATTO S, ZHAO H, TSITSIRIS H, HILD F, GIRARD Y. Shock enhancement of cellular structures under impact loading: Part I. Experiments [J]. Journal of the Mechanics and Physics of Solids, 2007, 55(12): 2652-2671.
[13] EDWIN RAJ R, PARAMESWARAN V, DANIEL B S S. Comparison of quasi-static and dynamic compression behaviour of closed-cell aluminium foam [J]. Materials Science and Engineering A, 2009, 526: 11-15.
[14] WANG Zhi-hua, JING Lin, ZHAO Long-mao. Elasto-plastic constitutive model of aluminium alloy foam subjected to impact loading [J]. Transactions of Nonferrous Metals Society of China, 2011, 21(3): 449-454.
[15] ABAQUS/EXPLICIT. User’s manual, version 6.9 [M]. France: Dassault Systèmes Simulia Corporation, 2009.
[16] MONDAL D P, GOEL M D, DAS S. Compressive deformation and energy absorption characteristics of closed cell aluminium-fly ash particle composite foam [J]. Materials Science and Engineering A, 2009, 507: 102-109.
[17] ASTM E112-10. Standard test methods for determining average grain size [S]. Pennsylvania, USA, ASTM, 2011.
[18] CHEN W, ZHANG B, FORRESTAL M J. A split Hopkinson bar technique for low-impedance materials [J]. Experimental Mechanics, 1999, 39: 81-85.
[19] KOLSKY H. An investigation of the mechanical properties of materials at very high rates of loading [C]//Proceedings Physics Society. London: Institute of Physics (Journal) Ltd., 1948: 676-700.
[20]  I, TEIXEIRA-DIAS F, MIRANDA V,
I, TEIXEIRA-DIAS F, MIRANDA V,  - CASTELLANOS J L. Numerical modelling of the dynamic compression of a closed-cell aluminium foam [C]//Iberian Conference on Fracture and Structural Integrity. Porto, Portugal: Emerald Group Publishing Limited, 2010.
- CASTELLANOS J L. Numerical modelling of the dynamic compression of a closed-cell aluminium foam [C]//Iberian Conference on Fracture and Structural Integrity. Porto, Portugal: Emerald Group Publishing Limited, 2010.
[21] DESHPANDE V S, FLECK, N A. Isotropic constitutive models for metallic foams [J]. Journal of the Mechanics and Physics of Solids, 2000, 48(6-7): 1253-1283.
[22] HASAN A, HAMID R, ARIFFIN A K, GANI R. Stress—strain behaviour of normal strength concrete subjected to high strain rate [J]. Asian Journal of Applied Sciences, 2010, 3(2): 145-152.
Manmohan DASS GOEL1, VASANT A. MATSAGAR2, Anil K. GUPTA1, Steffen MARBURG3
1. CSIR-Advanced Materials and Processes Research Institute (AMPRI), Council of Scientific and Industrial Research (CSIR), Bhopal-462 064, India;
2. Department of Civil Engineering, Indian Institute of Technology (IIT) Delhi, New Delhi-110 016, India;
3. Department of Aerospace Engineering, University of German Armed Forces, Neubiberg - 85577, Munich, Germany
摘 要:随着金属泡沫在工程应用中的增加,对它们在不同应变速率下的动态行为进行研究是有必要的。采用熔体发泡法制备闭孔粉煤灰泡沫铝,并对其在应变速率从700 s-1增加到1950 s-1时的应力—应变行为进行研究。使用商用有限元软件Abaqus/Explicit对分离式霍普金森压杆(SHPB)的数学模型进行模拟。实验和模拟结果证实了数学模型是可用的。研究了应变速率对抗压强度和能量吸收的影响,得到了多种应变率下的应力—应变曲线。结果表明,闭孔粉煤灰泡沫铝对应变速率是敏感的。
关键词:高应变速率;泡沫金属; 应变速率敏感性;数值模拟;分离式Hopkinson压杆
(Edited by Hua YANG)
Corresponding author: Manmohan DASS GOEL; Tel: +91-755-2457244; E-mail: mdgoel@ampri.res.in
DOI: 10.1016/S1003-6326(13)62569-8

