平面框架弹塑性分析的增量内力塑性系数法

文颖，曾庆元

(中南大学 土木工程学院，湖南 长沙，410075)

摘要：提出一种分析框架结构弹塑性响应的新方法即增量内力塑性系数法。由该方法直接得到结构弹塑性增量割线刚度矩阵,并据此提出直接迭代算法求解结构增量平衡方程。研究结果表明：直接迭代算法与经典的牛顿－拉夫逊方法相比，它不用数值积分形成结构弹塑性切线刚度矩阵，也无需在每次迭代步中计算结构整体不平衡力，简化了计算过程；弹塑性增量割线刚度矩阵可以显式给出，减少了计算工作量，且计算结果与经典解析解以及其他数值解十分接近；采用增量内力塑性系数法分析一般平面框架只需采用至多２个单元离散框架构件就可以得到足够的计算精度。

关键词：弹塑性分析；弹塑性刚度矩阵；增量割线刚度矩阵；增量内力塑性系数法；直接迭代算法

中图分类号：TU312          文献标志码：A         文章编号：1672-7207(2012)06-2295-05

Elasto-plastic analysis of planar frames by plastic-coefficient method based on incremental member forces

WEN Ying, ZENG Qing-yuan

(School of Civil Engineering, Central South University, Changsha 410075, China)

Abstract: An accurate and efficient numerical procedure, referred to as the plastic-coefficient method based on the incremental member forces, was presented for the nonlinear inelastic analysis of planar frames. Based on the elasto-plastic stiffness matrix derived from this new method, the direct-iteration solution scheme was developed to solve the incremental equilibrium equations. The results show that compared to the Newton-Raphson method, the direct-iteration solution scheme is unnecessary to construct the tangent stiffness matrix or to calculate the out-of-balance force during each iterative step. The elasto-plastic stiffness matrix is explicitly given herein, hence, the entire analysis procedure is greatly simplified without any loss of accuracy, and the results are very close to the analytical results from limit analysis and the numerical results from other methods. The proposed method can be applied to analyze frames with sufficient accuracy using at most two elements per member.

Key words: elasto-platic analysis; elasto-plastic stiffness matrix; incremental secant stiffness matrix; plastic-coefficient method based on incremental member forces; direct iteration method

传统的结构弹塑性极限强度分析一般采用经典的塑性铰理论，但该方法只能计算极限荷载，无法考虑结构构件弹塑性发展的全过程^[1]，特别是用于大型复杂结构的弹塑性分析时，需事先知道塑性铰出现的先后次序及位置，分析过程繁琐。随着矩阵结构分析理论应用的深入和高速电子计算机的快速发展，有限元方法已广泛用于求解一般结构弹塑性响应分析问   题^[2]。目前，国内外研究者采用的弹塑性有限元分析模型主要分为2类：塑性铰法和塑性区域法。塑性铰法假定塑性变形集中在构件端部而构件中间部分保持弹性工作，该法分析过程简单，但是，考虑构件塑性发展过程非常粗糙和近似。为了保证塑性铰法分析模型与构件实际弹塑性分布尽量接近，提高分析精度，Kim等^[3]提出三铰梁模型，在构件中点增设1个塑性铰考虑塑性沿构件长度方向的发展，采用纤维单元模型考虑塑性沿构件截面扩展；Attalla等^[4]提出伪塑性铰法，通过引入基于内力的初始屈服面和继生屈服面等概念以及构件整体受力平衡条件考虑塑性在构件内部发展全过程；Ren等^[5]提出刚体-弹簧模型，建立平面框架结构内力塑性屈服面方程以取代基于应力的塑性分析模型，提高分析效率；Krishnan^[6]提出改进的塑性铰法，认为构件塑化部分不再局限于节点，而是集中分布在靠近节点的有限区域，采用静力凝聚消除构件内部自由度；颜全胜^[7]提出内力塑性系数法，假定构件塑性系数沿长度方向线性分布；Liew等^[8]提出精细化塑性铰法，引入截面塑性发展系数考虑塑性沿截面的发展，假定该系数沿杆长抛物线变化近似考虑塑性沿长度方向的分布。塑性区域法^[9-10]将构件内部分成完全弹性区、塑性区和弹塑性区，考虑塑性沿整个构件的逐步开展，由于没有引入简化近似假定，一般被视为结构弹塑性分析的精确方法。其缺陷是由于将构件沿截面以及长度方向划分为若干有限段，增加数据处理量和计算机时而使得分析过程繁琐。在此，本文作者根据有限元分析的基本概念，提出杆系结构弹塑性分析的单元节点截面增量内力塑性系数法，通过引入单元平衡条件，简便地保证了单元的整体平衡，也自动考虑塑性沿单元长度方向的发展。该法显式推导了单元弹塑性增量割线刚度矩阵，避免了数值积分，提高了分析效率。基于该方法，提出求解结构非线性增量平衡方程的基于增量割线刚度的直接迭代算法。该算法在平衡迭代中不需计算结构切线刚度矩阵，也不需计算结构整体不平衡力，简化了迭代过程。

1  框架结构弹塑性分析的增量内力塑性系数法

1.1  弹塑性增量平衡方程

假定任意离散化结构在节点荷载P作用下节点变位为u，结构内部应力为σ，应变为ε。假定结构产生虚位移δu和虚应变δε，根据虚功原理，结构的虚应变能等于外力虚功，可以得到：

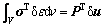             (1)

式中：ΔP为施加的荷载增量；Δu为节点位移增量；Δσ和Δε分别为结构应力和应变增量。由虚功原理，忽略几何位形改变对结构平衡的影响，在荷载P+ΔP作用下，结构平衡方程如下：

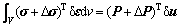      (2)

将(2)式减(1)式，可得：

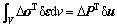                (3)

式(3)实际上就是小变形条件下增量形式的虚功原理，反映了结构增量平衡条件。不考虑材料非线性的影响，由式(3)可以直接得出线弹性结构平衡方程：

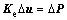                  (4)

考虑弹塑性分析,由式(3)可得到结构弹塑性增量平衡方程：

                (5)

式中：K_ep为结构弹塑性增量割线刚度矩阵。

1.2  梁单元弹塑性刚度列式的增量内力塑性系数法

从有限元法的物理概念来说，式(5)表示结构节点截面的抗力增量和外荷载增量的平衡。随着外荷载的增加，结构材料弹塑性行为集中反映在节点截面抗力增量降低，这是相对于单元为完全弹性时的抗力增量而言的。为此，可以定义节点截面弹塑性抗力增量和弹性抗力增量的比值(称为单元增量内力塑性系数)来反映构件弹塑性发展情况，并利用该系数来确定单元弹塑性刚度矩阵，最后采用“对号入座”法则^[11]得到结构弹塑性刚度矩阵。

首先，考虑单元为完全弹性时的情况，单元的平衡条件可写为：

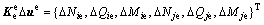     (6)

式中，等号右端各项表示节点截面弹性抗力增量，下标“e”表示单元处于弹性状态，上标“e”表示任意结构单元。若考虑单元已经屈服，则单元的平衡条件可改写为：

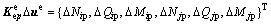   (7)

式中，等号右端各项表示节点截面弹塑性抗力增量，下标“ep”表示单元处于弹塑性状态。需要说明的是：与式(6)类似，式(7)的表现形式可由经典有限单元法 得到。

式(6)直接给出了弹性节点内力的计算表达式。一般假定单元的弹塑性状态只由正应力决定，弯曲剪应力不影响屈服，对于平面结构，多个实例已证实该假定合理性^[2,9]。为了考虑塑性区沿单元截面高度的扩展，这里采用纤维单元法^[2,9,12-14]即将单元截面细分成很多小块 (如图1所示)，用小块中点的应变、应力代表小块的应变、应力水平。累加所有小块对于截面内力的贡献，则有：

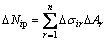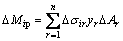，            (8)

其中：下标i为节点截面编号；r为截面上小块编号；ΔA_r为第r小块的面积；x_r和y_r为第r小块几何中心的截面形心坐标；Δσ_ir为i节点截面上第r小块弹塑性正应力增量，该应力增量一般根据材料单向应力状态下本构关系模型和应变增量得到。需要说明的是：目前比较流行的考虑塑性沿截面开展的途径是通过截面数值积分^[10]，尽管数值积分与纤维单元法相比减少了数据存储量和计算工作量，但应用范围较窄。例如，对于组合材料(钢筋混凝土)截面的塑性分析就不适用，因此，本文考虑到分析方法的通用性，选择纤维单元法。基于上述分析结果，定义下列单元增量塑性系数：

；；

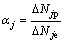；          (9)

式中：α_i和β_i分别为i节点截面的轴力和弯矩增量塑性系数；α_j和β_j与j节点截面相关。这里“增量”一词的用意是强调计算这些塑性系数是基于内力增量而不是全量。

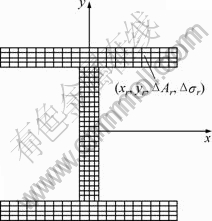
图1  梁截面分块示意图

Fig.1  Discretized cross-section of beam

与正应力的计算不同，弹塑性弯曲剪应力无法通过材料本构关系得到。为了简化，一些研究者通过计算弹性弯曲剪力增量作为替代^[2]，这显然破坏了单元整体平衡条件，导致出现计算误差。为了克服这种不足，可以利用处于弹塑性状态的单元平衡条件计算节点截面剪力增量，考虑式(7)等号右端的弹塑性抗力增量在单元内部自相平衡，有：

；

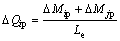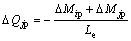          (10)

式中：各节点内力的正方向和传统有限元的规定一致；L_e为单元的长度。将式(10)代入式(7)有：

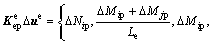
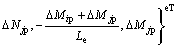          (11)

由式(6),(9)和(11)，可得弹塑性刚度矩阵和线弹性刚度矩阵有如下关系：

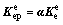
 (12)

式中：α为单元增量内力塑性系数矩阵，它只与轴力和弯矩的增量塑性系数有关。

1.3  非线性增量平衡方程求解步骤

用增量内力塑性系数法分析结构弹塑性响应的具体步骤如下。

(1) 假定结构弹性极限节点荷载为P⁰，节点位移、内部应变和应力分别为u⁰，ε⁰和σ⁰。在结构开始屈服时就采取增量加载模式，施加荷载增量ΔPⁱ，i表示荷载增量步。选取初始刚度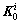：当i=1时，；当i≥2时，。

(2) 进入平衡迭代。采用高斯消元法求解线性方程组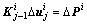，得到第j迭代步节点位移近似值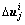。当j=1时，根据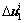，计算单元增量内力塑性系数，得α，按照式(12)更新单元弹塑性刚度矩阵，进而由“对号入座”法则形成结构弹塑性增量割线刚度矩阵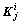；当j≥2时，首先判断平衡迭代收敛条件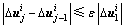是否满足(ε为任意微量，一般取作0.1%)，若满足，则转入步骤(4)；否则，与j=1时的情形相同，根据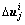最终形成。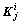

(3) 将步骤(2)中得到的更新的结构弹塑性刚度矩阵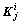又代回步骤(2)，继续平衡迭代。与此同时，j=j+1。

(4) 步骤(2)中的平衡迭代收敛后，累加外部荷载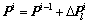，更新结构状态变量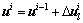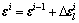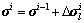：，，。其中，l为本次迭代步的总迭代次数。

(5) 继续加载，i=i+1，求解流程回到步骤(1)，直至结构达到承载极限状态为止。结构极限状态由本步刚度参数法^[13]确定。

增量-迭代求解过程的图解形式如图2所示。

图2  基于增量割线刚度的增量-迭代过程

Fig.2  Incremental secant stiffness based on incremental-iterative procedure

2  数值算例

算例1  文献[1]计算了简支梁在跨中集中荷载作用下的弹塑性响应，为了与文献[1]中的数值结果进行比较，本算例采用相同的几何和材料参数(见文献[1])。文献[1]将梁横截面等分成8层，沿梁轴方向划分为20个梁段，而这里也将截面分成上下8层，沿梁跨方向划分为2个梁段，公共节点位于跨中。简支梁荷载-挠度曲线如图3所示。文献[1]采用分段分块变刚度法计算所得到的结构极限荷载P≈2.8×10⁶ N，由增量内力塑性系数法得P≈2.689 3×10⁶ N，而结构弹塑性极限强度的理论值为P≈2.688×10⁶ N。文献[1]中的极限荷载值偏大的原因可能是计算剪切恢复力时用采用弹性剪力而不是弹塑性剪力，导致结构平衡条件只在节点处满足，结构单元内部平衡条件不满足。

算例2  如图4所示，一单层两榀平面框架承受面内若干集中荷载作用。至于其弹塑性响应，Franchi等^[15]采用数学规划法计算弹塑性极限荷载，Wong等^[16]采用分段线性化内力屈服面法分析结构弹塑性响应全过程。该框架几何与材料见在文献[15]。这里将所有柱子离散为1个梁单元，横梁用2个单元模拟。所有杆件节点截面沿其厚度方向统一划分成10个条带。图5所示为荷载-框架顶部侧移曲线，并与现有其他文献结果进行对比。

图3  简支梁的荷载-位移曲线

Fig.3  Load deflection curves of simple supported beam

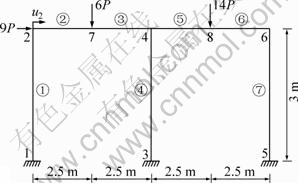
图4  平面框架

Fig.4  One storey portal frame of simple supported beam

图5  平面框架的荷载-侧移曲线

Fig.5  Load-top horizontal displacement curve of portal frame

按本文方法算得悬臂梁的极限荷载因子  λ=0.768 7，而文献[15]和文献[16]给出的极限荷载因子分别为0.768 5和0.768 9，它们都非常接近。值得注意的是：当荷载因子λ=0.745时，3和4号节点处塑性铰出现弹性卸载。这也是结构发生塑性变形后内力重新调整的结果，这一现象在文献[15]和[16]中得到证明。

3  结论

(1) 提出了平面框架弹塑性分析的增量内力塑性系数法。通过引入单元平衡条件，自动地考虑塑性沿单元长度方向的发展，得到的单元弹塑性增量割线刚度矩阵可以显式给出，无需数值积分，提高了计算   效率。

(2) 增量内力塑性系数法的计算步骤与经典弹塑性有限元分析法的相比无需计算结构切线刚度矩阵，也不需在每次迭代中计算不平衡力，简化了迭代计算过程。

(3) 增量内力塑性系数法不仅物理概念明确，而且计算结果正确、可靠。在分析一般框架结构时，每个构件用至多2个梁单元离散便可以获得满意结果。

参考文献：

[1] 潘家英, 张国政, 程庆国. 大跨度桥梁极限承载力的几何与材料非线性耦合分析[J]. 土木工程学报, 2000, 33(1): 5-9.
PAN Jia-yin, ZHANG Guo-zheng, CHENG Qing-guo. Geometrical and material nonlinear analysis for determining ultimate load capacity of long-pan bridges[J]. China Civil Engineering Journal, 2000, 33(1): 5-9.

[2] Hinton E, Owen D.R.J. Finite elements in plasticity: Theory and practice[M]. Swansea: Pineridge Press, 1979: 3-7.

[3] Kim S E, Kim Y, Choi S H. Nonlinear analysis of 3-D steel frames[J]. Thin Walled Structures, 2001, 39(6): 445-461.

[4] Attalla M R, Deierlein G G, McGuire W. Spread of plasticity: Quasi-plastic hinge approach[J]. Journal of Structural Engineering, 1994, 120(8): 2451-2473.

[5] Ren W X, Tan X G, Zheng Z C. Nonlinear analysis of plane frames using rigid body-spring discrete element method[J]. Computers & Structures, 1999, 71(1): 105-119.

[6] Krishnan S. Modified elastofiber element for steel slender column and brace modeling[J]. Journal of Structural Engineering, ASCE, 2010, 136(11): 1350-1366.

[7] 颜全胜. 大跨度钢斜拉桥极限承载力分析[D]. 长沙: 长沙铁道学院土木工程系, 1994: 33-37.
YAN Quan-sheng. Analysis of ultimate load capacity of the steel cable-stayed bridge[D]. Changsha: Changsha Railway University. Department of Civil Engineering, 1994: 33-37.

[8] Liew J Y R, White D W, Chen W F. Second-order refined plasti-hinge analysis for frame design: Part I and Part II [J]. Journal of Structural Engineering, ASCE, 1993, 119(11): 3196-3237.

[9] Toma S. European calibration frames for second-order inelastic analysis[J]. Engineering Structures, 1992, 14(1): 7-14.

[10] Teh L H, Clarke M J. Plastic-zone analysis of 3D steel frames using beam elements[J]. Journal of Structural Engineering, ASCE, 1999, 125(11): 1328-1337.

[11] 曾庆元, 杨平. 形成矩阵的“对号入座”法则与桁梁空间分析的桁段有限元法[J]. 铁道学报, 1986, 8(2): 48-59.
ZENG Qing-yuan, YANG Ping. The “set-in-right-position” rule for formulating matrix and the truss finite element method for spatial truss analysis[J]. Journal of the Railway Society, 1986, 8(2): 48-59.

[12] Zhang Y X, Bradford M A, Gilbert R I. A new triangular layered plate element for the non-linear analysis of reinforced concrete slabs[J]. Communications in Numerical Methods in Engineering, 2005, 22(7): 699-709.

[13] 韦成龙. 大跨度板桁结合主梁斜拉桥极限承载力分析[D]. 长沙: 中南大学土木工程学院, 2003: 80-83.
WEI Cheng-long. Analysis of the ultimate load for long span cable-stayed bridge with a plate-truss composite beam[D]. Changsha: Central South University. School of Civil Engineering, 2003: 80-83.

[14] 吕烈武, 沈世钊, 沈祖炎, 等. 钢结构构件稳定理论[M]. 北京: 中国建筑工业出版社, 1983: 246-252.
L? Lie-wu, SHEN Shi-zhao, SHEN Zu-yan, et al. The stability theory of steel members[M]. Beijing: China Architecture & Building Press, 1983: 246-252.

[15] Franchi A, Cohn M Z. Computer analysis of elastic-plastic structures[J]. Computer Methods in Applied Mechanics and Engineering, 1980, 21(3): 271-294.

[16] Wong M B, Loi F T. Yield surface linearization in elasto-plastic analysis[J]. Computers and Structures, 1987, 26(6): 951-956.

(编辑 陈灿华)

收稿日期：2011-06-22；修回日期：2011-08-19

基金项目：国家自然科学基金资助项目(51108460)；中国博士后科学基金面上资助项目(2012M511409)；教育部博士点基金资助项目(20010533004)；中南大学博士后基金资助项目(2010年)

通信作者：文颖(1981-)，男，湖南长沙人，博士，讲师，从事结构非线性稳定分析及极限承载力研究；13975126639；E-mail：ywen_ce@csu.edu.cn