基于GA和BP混合算法的水下机器人系统建模

王建国¹，姜春萌²，孙玉山³，何斌³，李吉庆³

(1. 中国舰船研究设计中心，湖北 武汉，430064；

2. 武汉科技大学城市学院 人文学部, 湖北 武汉，430083；

3. 哈尔滨工程大学 水下机器人技术国防科技重点实验室，黑龙江 哈尔滨，150001)

摘要：借鉴Jordan和Elman神经网络的优点，构造一种新型的动态神经网络。将基于遗传算法(GA)和误差反传算法(BP)的混合算法用于神经网络的权值调整。为了提高收敛速度，避免系统陷于局部极小值。将改进的神经网络应用于水下机器人系统建模。仿真结果表明，该网络能对隐含层的历史状态进行记忆，并实现在线调整历史信号对当前值的影响，并且增加了输出层节点的反馈以增强神经网络的信号处理能力。基于混合算法的神经网络提高了学习的收敛速度和辨识精度。

关键词：水下机器人；系统辨识；神经网络；遗传算法；误差反传算法

中图分类号：TP24          文献标志码：A         文章编号：1672-7207(2011)S1-0427-05

Neural network identification of underwater vehicle by hybrid learning algorithm

WANG Jian-guo¹, JIANG Chun-meng², SUN Yu-shan³, HE Bin³, LI Ji-qing³

(1. China Ship Development and Design Center, Wuhan 430064, China;

2. Humanities Department, City College of Wuhan University of Science and Technology, Wuhan 430083, China;

3. State Key Laboratory of Autonomous Underwater Vehicle, Harbin Engineering University, Harbin 150001, China)

Abstract: A new dynamic neural network was constructed by borrowing ideas from Jordan and Elman neural networks. To accelerate the rate of convergence and avoid getting into local extremum, a hybrid learning algorithm by Genetic algorithm (GA) and error back propagation algorithm (BP) was used to tune the weight values of the network. Finally, the improved neural network was utilized to identify the AUV hydrodynamic model. The simulation results show that the new network can remember the history state of hidden layer and tune the effect of the past signal to the current value real-timely. And in the presented network, the feedback of output layer nodes is increased to enhance the ability of handling signals. The neural network by hybrid learning algorithm improves the learning rapidity of convergence and identification precision.

Key words: underwater vehicle; system identification; neural network; genetic algorithm; back propagation algorithm

随着科学的迅猛发展，控制系统越来越复杂，控制精度要求也越来越高，精确建模就尤为重要，因此，被控对象的系统建模在控制系统设计过程中占有重要地位^[1]，即使是采用模糊逻辑控制等这类不依赖于被控对象精确数学模型的控制策略，在设计、分析和仿真过程中，准确的系统输入输出特性的获得^[2]使设计的参数更加接近实际系统，所以系统建模作为控制理论的重要分支，具有相当重要的意义。对于水下机器人来说，由于其运动具有多自由度、强非线性和时变特性，同时由于每次作业任务要求搭载的传感器发生变化使得其形状和质量平衡发生变化，运动特性也随之改变，对于这种动态的非线性系统传统的建模方法有很大的局限性。由于神经网络具有以任意精度逼近任意非线性映射的能力；采用动态的神经网络，加之改进的混合算法通过运动数据直接来辨识水下机器人的运动特性，即用神经网络来建立水下机器人的运动模型，可以作为自适应控制器的辨识器，为故障诊断提供信息等，因此对智能水下机器人这种复杂的非线性系统进行辨识将具有重要的理论意义和实用价值。本文作者采用一种新型的动态神经网络，该网络考虑了各层网络各层神经元的反馈信息对网络的信号处理能力影响，并且将GA算法与BP算法用于其网络权值的修正，试验结果说明该网络可以提高收敛速度及精度。

1  动态神经网络模型

前向神经网络实现的是静态映射，没有延迟线的帮助，不能表示动态系统的映射关系。即使对动态系统的仿真也可以采用带延迟的前馈网络^[3](TDNN)来实现，但如果只对输入空间进行重构，则TDNN只有仿真有限冲击响应的能力，而回归网络(RNN)则有仿真无限冲击响应的能力，这使得RNN能仿真更高阶的动态系统^[4]。RNN内建的状态记忆机制实际上起到了对信号进行加权滑动平均处理的作用，因此，RNN天生就具有一定的滤波能力。RNN仿真同样阶数的动态系统需要更少的节点和联接，所提供的输入输出更具有实际物理意义。

根据现在常用的Jordan网络和Elman网络的优点，构造如图1所示的网络模型结构。该结构结合了2个网络的特点，将隐含层的输出反馈到结构层，对隐含层的历史进行状态记忆，对于不同的输入信号可以调整过去的信号对现在值的影响。将输出层的值反馈到输入层，根据输出值来修正网络。

式(1)~(4)分别表示隐含层、关联层、输出层和输出反馈的关系。

        (1)

               (2)

              (3)

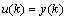，m≤k≤r            (4)

图1  改进的动态神经网络结构

Fig.1  Structure of improved dynamic neural network

2  混合学习算法

2.1  BP算法及改进

由于BP(Back Propagation)学习算法具有结构简单、算法成熟且具有很强的非线性映射能力，它是按照误差最速下降方向搜索，只要学习因子适当^[5]，其收敛效率很高。

考虑如下总体误差目标函数E，

                 (5)

其中，。

隐含层到关联层：

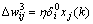             (6)

输入层到隐含层：

            (7)

关联层到隐含层：

          (8)

  (9)

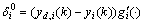
           (10)

式中，i=1，2，…，m；j=1，2，…，n；q=1，2，…，r。

针对BP算法收敛速度慢，作如下改进：

 (11)

式中：为k时刻的负梯度，η为动量因子，0＜η＜1，α为学习率，α＞0，，其中，。

2.2  遗传算法(GA)

遗传算法是一种随机搜索算法，它将达尔文的“优胜劣汰，适者生存”这一基本生物进化原理引入待优化参数形成的编码串群体中，并在串群中进行有组织又随机的遗传操作，随着算法的进行，优良的品质被逐渐保留并加以组合，从而产生更佳的个体^[6]，直至最后获得满足一定条件的最优解。

基本步骤为：

(1) 初始化种群，将神经网络权值用随机实数编码成个体基因。

(2) 适应度变换，取适应度函数为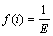，并采用线性变换：

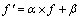             (12)

其中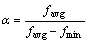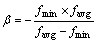，，，分别为群体中最小和平均适应度值。

(3) 选择算子操作，采用无回访余数随机选择。

(4) 交叉操作，为了最大程度保证进化中的个体的多样性和优良模式的稳定性，采用排序分组交叉操作。采用交叉公式和交叉率如下：

        (13)

   (14)

式中：f_max为群体中最大适应度；P_c1，P_c2为0和1之间的常数，此处取P_c1=0.85，P_c2=0.55。

具体操作过程如下：首先将个体的适应度按降序排序，然后将父辈个体按一定比例分为2组，在适应度较高的一组中，取适应度最高的个体作为父本，与该组其余个体分别按概率交叉，同时保留适应度最高的个体。对适应度较低的一组，采用相邻个体交叉方式，一方面保证种族进化的相对平稳，另一方面，不排除在适应度较差的个体间发现一个适应度相对高的个体的可能。

(5) 变异操作，采用高斯变异，对于浮点数编码策略，在个体V中随机选择一个变量V_k，对V_k变异后的结果服从以V_k为均值的高斯分布。

2.3  基于GA＆BP混合算法

BP算法本质上是一种误差梯度下降算法，对于复杂的非线性寻优问题，最大缺点在于容易陷入局部极小值。GA是一种随机搜索算法，能在概率的意义上收敛到全局最优点，其收敛过程不是BP算法的渐变式，而往往带有突变式的特点，GA的缺点在于收敛到一定程度的时候，通过交叉、变异算子产生更高适应性的个体的概率显著降低^[7]，从而收敛速度受到制约。在GA与BP的混合算法中，GA并行搜索多个目标点，可以提高初始权值的鲁棒性，BP算法再将优秀个体进行局部微调，这样既可以提高收敛速度又能避免陷于局部极小，从而提高了学习算法的效率。

采用GA＋BP混合学习算法的具体步骤如下。

第1步：初始化规模为S的种群，其各个个体分别对应神经网络的权值。

第2步：对于每个个体，根据神经网络运算其输出结果，并根据样本输出和误差评价函数计算出各个个体的适应度值。如果有一个适应度值满足精度要求则结束学习；否则进行下一步。

第3步：按照无回放余数随机选择策略进行选择。

第4步：对父本进行自适应交叉和变异操作得到新一代种群。

第5步：将每一个个体以一定概率进行一次BP搜索，取代父本，最优个体一定进行一次BP搜索。

第6步：循环操作，转向第2步。

3  水下机器人仿真辨识试验

水下机器人完成了实体试验。水下机器人实体试验的试验区域情选择在长×宽×高为50 m×30 m×10 m的三维区域。根据数学模型实际要求以及现实条件场地的限制，水下机器人主要工作状态可考虑为水平面的运动和垂直面运动。设计的试验为水下机器人以设计的正弦电压输入激励下的定深航行，由控制系统向推力器发出推力指令，自动控制侧推保持艏向直航。采集的数据样本包括6个推力器的输入指令(控制电压)、纵向速度和横向速度，对机器人的2个主推力器施以正弦电压，同时对4个侧推力器(前后各2个)输入方波电压，充分激励机器人水平面的运动特性。试验中采样周期为0.5 s，待水下机器人进入稳定工作状态开始采样，达到一定采样长度结束实验。这样就得到网络训练样本数据。

采用上述动态神经网络进行了水下机器人系统辨识仿真试验，2个主推进器及4个测推进器电压作为网络输入数据，输出数据为纵向速度、横向速度及摇艏角速度。网络隐含层节点数选为10个，种群规模150，训练步长为0.02，利用水池试验获得的实验数据进行网络训，图2~4所示分别为网络输入输出数据及训练后误差比较结果。

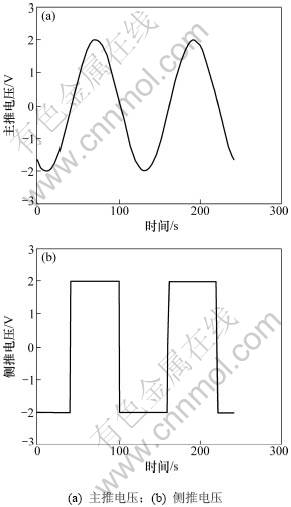
图2  网络输入数据

Fig.2  Inputs of neural network

根据试验结果可知，对于单自由度的运动辨识，采用简单前向神经网络就能达到一定效果，但对于多自由度运动(这样与机器人实际运动情况更为接近)，由于具有很强的耦合性，其内部特性复杂，采用BP网络学习、辨识，其结果在1 000次学习内难以收敛，而采用动态网络并利用遗传算法与BP算法结合，不仅收敛速度快，而且辨识精度比单一采用GA学习算法有很大的提高。

图3  网络输出与仿真试验输出对比

Fig.3  Comparing between network outputs and simulation outputs

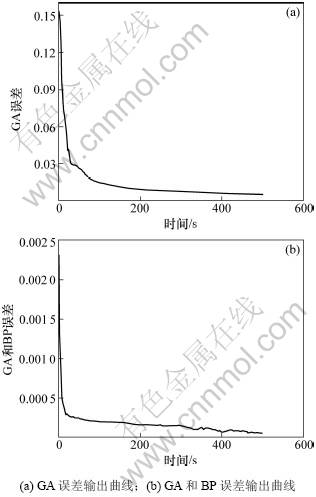
图4  GA与GA&BP算法误差对比

Fig.4  Error comparing between GA and GA&BP algorithms

4  结论

在给出动态回归神经网络模型的基础上，充分利用具有局部微调能力的BP算法与GA算法各自的优势，构造出混合学习算法，实现了强非线性动态系统—水下机器人的运动建模，克服了前向BP网络难以收敛或是收敛速度慢的问题，而且提高了精度。

参考文献：

[1] 王建国, 万磊, 甘永,等. 嵌入式数据库在水下机器人中的应用研究[J]. 哈尔滨工程大学学报, 2008, 29(9): 897-901.
WANG Jian-guo, WAN Lei, GAN Yong, et al. Embedded database applied in underwater vehicles[J]. Journal of Harbin Engineering University, 2008, 29(9): 897-901.

[2] 张铭钧, 胡明茂. 基于稳态自适应技术的水下机器人系统在线辨识[J]. 系统仿真学报, 2008, 20(8): 5006-5009.
ZHANG Ming-jun, HU Ming-mao. Online identification of autonomous underwater vehicle based on stable adaptive technique[J]. Journal of System Simulation, 2008, 20(8): 5006-5009.

[3] 谢海斌, 沈林成. 水下机器人动态系统协同建模方法研究[J].系统仿真学报, 2007, 19(9): 2130-2133.
XIE Hai-bin, SHEN Lin-cheng. Collaborative modeling of underwater vehicle dynamic system[J]. Journal of System Simulation, 2007, 19(9): 2130-2133.

[4] Narendra K S, Parthasarathy K. Identification and control of dynamical system using neural networks[J]. IEEE Trans Neural Networks, 1990, 1(1): 4-27.

[5] YU Jian-cheng, ZHANG Ai-qun, WANG Xiao-hui. Direct adaptive control of underwater vehicles based on fuzzy neural networks[J]. Acta Automatica Sinica, 2007, 33(8): 840-846.

[6] Pepijn W J, Ven V D, Johansen T A, et al. Neural network augmented identification of underwater vehicle models[J]. Control Engineering Practice, 2007, 15(6): 715-725.

[7] 王建国, 吴恭兴, 万磊, 等. 广义S面的水下机器人控制器设计[J]. 电机与控制学报, 2009, 13(1): 144-147.
WANG Jian-guo, WU Gong-xing, WAN Lei, et al. Controller design of underwater robots based on generalized S-plane[J]. Elcetric, Achines and Control, 2009, 13(1): 144-147.

(编辑 赵俊)

收稿日期：2011-04-15；修回日期：2011-06-15

基金项目：国家自然科学基金资助项目(50579007)；国家“863”计划项目(2008AA092301)；中国博士后科学基金资助项目(20100480964)

通信作者：王建国(1983-)，男，湖南常德人，博士，从事水下航行体智能控制和系统集成研究；电话：13277036071；E-mail：wjg103@126.com