文章编号:1004-0609(2015)04-0835-09
对流作用下镁合金凝固组织演变的数值模拟
杨满红1,郭志鹏1,熊守美1, 2
(1. 清华大学 材料学院,北京 100084;
2. 清华大学 汽车安全与节能国家重点实验室,北京 100084)
摘 要:基于改进元胞自动机模型和流场传输模型,模拟对流作用下的镁合金等轴晶和柱状晶组织演变过程。采用改进元胞自动机模型模拟具有密排六方结构的镁合金的枝晶生长;采用投影法求解流场传输模型耦合质量守恒方程、动量守恒方程和溶质扩散方程。不仅模拟了镁合金中单枝晶、多枝晶和柱状晶在对流作用下的生长规律,还对不同入流速度下枝晶凝固前沿的溶质分布进行定量分析。模拟结果表明:迎流端枝晶生长较快,二次枝晶臂较为发达;背流端生长缓慢,二次枝晶臂较细小或没有二次晶臂。对流作用还会改变等轴枝晶扩散层的分布,在背流端扩散层呈拖曳特性。因此,对流作用对镁合金凝固组织的演变有重要影响。
关键词:镁合金;枝晶生长;对流;元胞自动机
中图分类号:TG111.4 文献标志码:A
Numerical simulation of dendritic growth of magnesium alloy with convection
YANG Man-hong1, GUO Zhi-peng1, XIONG Shou-mei1, 2
(1. School of Materials Science and Engineering, Tsinghua University, Beijing 100084, China;
2. State Key Laboratory of Automobile Safety and Energy, Tsinghua University, Beijing 100084, China)
Abstract: A model, which is based on modified cellular automaton (CA) and momentum transport, was used to model equiaxed and columnar dendritic growth of magnesium alloys with convection. The CA model was used to simulate dendritic growth of Mg alloy (hexagonal close-packed structure). The modified projection method was used to solve the flow field transport model coupled mass conservation equation, momentum conservation equation and solute diffusion equation. The growth laws of the single dendrite, multiple dendrites and columnar grain in Mg alloy were simulated, and the solute distributions of dendritic solidification front with different inflow velocities were analyzed quantificationally. The simulation results show that the dendrite growth at the upstream tip is faster than that at downstream, and secondary arms stretches intensively on the primary arms at the upstream tip, rather than that at the downstream where only a few weak or no secondary arms stretches. The flow also changes the distribution of the diffusion layer, and the diffusion layer, which spreads heavily at the downstream. Therefore, the convection has a major impact on the evolution of solidification microstructure of Mg alloy.
Key words: magnesium alloys; dendrite growth; convection; cellular automaton
镁合金由于具有低的密度、高比强度和比刚度、良好的阻尼性能和切削加工性能等优点,被誉为“21世纪的绿色工程材料”,在汽车、航空航天和3C产品等领域得到广泛研究与应用,如汽车仪表盘支架、航空发动机齿轮箱、笔记本外壳等[1-2]。镁合金零件的性能主要由凝固组织决定,在合金凝固过程中,液相流动对凝固组织有着重要影响,而镁合金枝晶组织是最常见的显微组织。因此,研究液相流动对枝晶组织的形貌、生长及分布的影响对调控镁合金凝固组织,以致提高镁合金零件的性能有着重要作用。
近些年,随着计算机技术的飞速发展,通过模拟技术研究微观组织的形貌与生长也得到了不断发展,常见的数值模拟模型包括相场模型(PF)和元胞自动机模型(CA)。国内外许多学者应用PF模型耦合流场计算了对流作用下枝晶的演变规律,研究内容由二维跨度到三维,并考虑了入流速度、浮升力等因素对枝晶演变过程的影响[3-10]。但由于相场模型网格尺寸一般在纳米量级,计算区域较小,且计算速度有局限性,尽管许多学者通过改进算法加速计算过程,相场模型的计算效率仍然较低。相比相场模型,CA模型以模拟尺度大、计算速度快等优势得到广泛研究。朱鸣芳等[11-12]将CA模型与动量传输和溶质传输结合,模拟了二维条件下Al-Cu合金单枝晶和多枝晶在强制对流以及自然对流下的枝晶生长过程。随后,孙东科等[13-14]和YIN等[15]将LBM方法耦合到CA模型中,提高了计算效率。而YUAN等[16]、石玉峰等[17-18]和张显飞等[19]又分别将对流下Ni-Nb、Al-Si、以及Al-Cu合金的枝晶生长扩展到了三维尺度。
然而,不同于Al-Cu,Ni-Nb等合金的面心立方(FCC)晶体结构,镁合金具有密排六方(HCP)晶体结构,在{0001}基面上沿着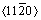 生长,并呈现六重对称特性。因此,势必要建立六重对称的数值模型来进行镁合金枝晶生长的研究。由于密排六方结构生长模型的复杂性,在考虑对流的镁合金显微组织研究中,大多都使用PF模型。袁训锋等[9]采用PF模型模拟了AZ91D镁合金在强制对流作用下的枝晶尖端生长行为,但模拟的镁合金枝晶形貌只显示了枝晶主干的生长行为,没有二次晶臂的演变过程。GUO等[7]和尧军平等[10]则分别呈现了具有六重对称枝晶形貌的模型合金和AZ91D镁合金枝晶主干以及二次晶臂的形态,再现了枝晶生长过程迎流端生长速度大于背流端的生长现象。然而,采用CA模型研究对流对镁合金等具有六重对称枝晶组织的形貌及生长的影响还鲜见报道。如前所述,CA模型在计算效率和计算尺度上较PF模型都有很大的优势,因此,本文作者采用CA模型耦合Navier-Stokes方程,实现了对流作用下的镁合金枝晶演变过程,模拟得到了强制对流下单个、多个等轴枝晶的生长过程,并考查了对流对不同取向镁合金等轴晶形貌的影响和不同入流速度对枝晶形貌的影响。同时,还模拟得到了对流对定向凝固过程柱状晶生长的影响规律。
生长,并呈现六重对称特性。因此,势必要建立六重对称的数值模型来进行镁合金枝晶生长的研究。由于密排六方结构生长模型的复杂性,在考虑对流的镁合金显微组织研究中,大多都使用PF模型。袁训锋等[9]采用PF模型模拟了AZ91D镁合金在强制对流作用下的枝晶尖端生长行为,但模拟的镁合金枝晶形貌只显示了枝晶主干的生长行为,没有二次晶臂的演变过程。GUO等[7]和尧军平等[10]则分别呈现了具有六重对称枝晶形貌的模型合金和AZ91D镁合金枝晶主干以及二次晶臂的形态,再现了枝晶生长过程迎流端生长速度大于背流端的生长现象。然而,采用CA模型研究对流对镁合金等具有六重对称枝晶组织的形貌及生长的影响还鲜见报道。如前所述,CA模型在计算效率和计算尺度上较PF模型都有很大的优势,因此,本文作者采用CA模型耦合Navier-Stokes方程,实现了对流作用下的镁合金枝晶演变过程,模拟得到了强制对流下单个、多个等轴枝晶的生长过程,并考查了对流对不同取向镁合金等轴晶形貌的影响和不同入流速度对枝晶形貌的影响。同时,还模拟得到了对流对定向凝固过程柱状晶生长的影响规律。
1 模型和算法
1.1 动量传输方程
镁合金溶液凝固过程中的液体流动受连续性方程和动量守恒方程控制,其中连续性方程为
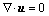 (1)
(1)
动量守恒方程为
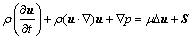 (2)
(2)
式中:u为液相流动速度;p为压力;S是源项,主要考虑浮升力等因素的影响; 为流体密度;
为流体密度;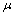 为流体黏度。相比强制对流,浮升力对流体流动的影响较小,可以忽略,故而在强制对流计算中不考虑浮升力的影响。
为流体黏度。相比强制对流,浮升力对流体流动的影响较小,可以忽略,故而在强制对流计算中不考虑浮升力的影响。
1.2 溶质传输方程
镁合金溶液凝固过程中的固相溶质扩散方程为
 (3)
(3)
考虑溶质扩散以及对流的影响时,镁合金溶液凝固过程中的液相溶质扩散方程为
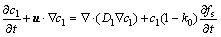 (4)
(4)
式中:cs和cl分别为固相和液相溶质浓度;Ds和Dl分别为固相和液相溶质扩散系数;k0为溶质平衡分配系数;fs为单元固相分数。式(4)中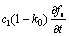 代表凝固过程中由于单元固相率的增加导致固液界面溶质排出对周围单元溶质浓度的影响。
代表凝固过程中由于单元固相率的增加导致固液界面溶质排出对周围单元溶质浓度的影响。
1.3 枝晶生长模型
在枝晶生长模型中,采用了本课题组前期算法[20],在界面曲率等计算方法中稍有改进。首先假设固液界面溶质局部平衡,满足以下关系:
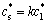 (5)
(5)
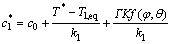 (6)
(6)
式中: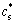 和
和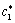 分别为界面平衡固相及液相溶质浓度;c0为合金初始浓度;
分别为界面平衡固相及液相溶质浓度;c0为合金初始浓度;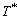 为界面温度;
为界面温度;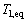 为c0处液相线温度;kl为液相线斜率;
为c0处液相线温度;kl为液相线斜率;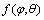 为界面能各向异性函数;
为界面能各向异性函数; 为Gibbs-Thomson系数;K为界面曲率。镁合金溶液凝固过程中的固液界面各向异性如下所示:
为Gibbs-Thomson系数;K为界面曲率。镁合金溶液凝固过程中的固液界面各向异性如下所示:
 (7)
(7)
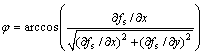 (8)
(8)
式中: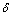 为各向异性系数;
为各向异性系数;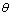 为枝晶优先生长方向与 x 轴之间的夹角;
为枝晶优先生长方向与 x 轴之间的夹角;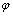 为界面法线与x轴之间的夹角。采用计数法[21]计算界面曲率K,计算公式如式(9)所示:
为界面法线与x轴之间的夹角。采用计数法[21]计算界面曲率K,计算公式如式(9)所示:
 (9)
(9)
式中:L是单元步长;N为界面单元的周围邻居单元个数;二维情况下N为8。在固液界面生长过程中,界面生长速度如式(10)所示:
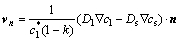 (10)
(10)
式中:vn为界面生长速度;n为固液界面法向。随后利用式(11)计算单元固相率:
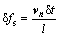 (11)
(11)
式中: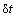 为微观时间步长;l为固相单元中心至界面单元中心的距离。对于镁合金HCP晶体结构的邻居单元定义,采用类似文献[22]的定义方式。
为微观时间步长;l为固相单元中心至界面单元中心的距离。对于镁合金HCP晶体结构的邻居单元定义,采用类似文献[22]的定义方式。
2 计算求解
2.1 材料物性参数
对压铸常见的AZ91和AM60两种合金进行模拟研究,考虑到这两种合金中主要元素为Mg和Al,且其它元素的含量较低,因此可将合金简化为Mg-Al二元合金。表1所列为镁合金AZ91和AM60的物性参数[23-25]。
2.2 数值计算算法
假设流体为不可压缩流体,基于交错网格采用投影法[26]求解连续性方程和动量守恒方程。根据所计算的速度场,利用无各向异性差分方式[27]求解溶质传输方程。在本研究中,通过在左边界施加一个入口速度并让流体从右边界流出,形成横向流动,并假定上下两个面为无滑移条件,无速度。
表1 AZ91和AM60镁合金的物性参数[23-25]
Table 1 Physical property parameters of AZ91 and AM60 magnesium alloys[23-25]
3 模拟结果及分析
3.1 对流作用下单个等轴枝晶的生长
基于考虑对流的镁合金枝晶生长数值算法,首先模拟了对流作用下单个等轴枝晶的生长。CA单元网格步长为2 μm,假定计算区域内温度场均匀,并以80 K/s的速率冷却,在强制对流作用下,入口速度为0和0.1 mm/s。在400×400个单元的计算域内放置一个形核核心,不考虑其他形核方式。为方便解释对流作用对枝晶形貌的影响,将受流体冲刷的一端称作迎流端,背对迎流端的称作背流端,与水平线呈60°朝左的两分支称作左侧60°分支,与水平线呈60°朝右的两分支称作右侧60°分支。图1所示为在无对流和强制对流作用下AZ91镁合金枝晶形貌的模拟结果。从图1可以看出,在无对流作用时,AZ91镁合金枝晶沿着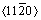 方向生长,枝晶各个分支呈60°夹角,且每个分支大小一致。当有对流作用时,枝晶呈现非对称生长。在迎流端,枝晶分支发达,二次枝晶臂亦较为发达;在背流端,枝晶分支生长相对细小,二次枝晶臂也较迎流端细小。模拟结果与使用PF模型[7, 10]模拟结果一致,但相较于PF模型,CA方法计算速度更快,计算域更大。
方向生长,枝晶各个分支呈60°夹角,且每个分支大小一致。当有对流作用时,枝晶呈现非对称生长。在迎流端,枝晶分支发达,二次枝晶臂亦较为发达;在背流端,枝晶分支生长相对细小,二次枝晶臂也较迎流端细小。模拟结果与使用PF模型[7, 10]模拟结果一致,但相较于PF模型,CA方法计算速度更快,计算域更大。
图2所示为当冷却速率为80 K/s、入流速度为0.1 mm/s时AZ91镁合金单个等轴枝晶的生长演变过程。由图2可知,随着凝固的进行,AZ91镁合金固相率不断增加,已凝固的固相将溶质排出到液相,并逐渐扩散到周围的液相中。在迎流端,枝晶受到流体的冲刷,溶质扩散层较窄,浓度梯度高,使枝晶尖端出现局部过冷度增大的现象;而在背流端,流体流经时,流速较小,对枝晶的冲刷也较弱,溶质扩散层较宽,浓度梯度较低,从固相排出到液相的溶质来不及扩散,溶质富集而阻碍枝晶的生长[17]。图3所示为迎流端和背流端枝晶生长速率随时间的变化。由图3可知,迎流端尖端生长速率大于背流端。因此,迎流端生长较快,枝晶呈现非对称生长。
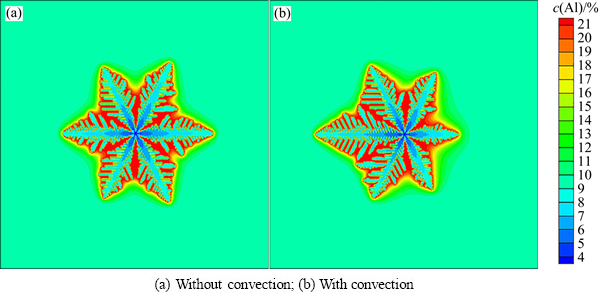
图1 AZ91镁合金等轴枝晶形貌模拟结果(入流速度为0.1 mm/s)
Fig. 1 Simulated results of equiaxed dendritic morphologies of AZ91 magnesium alloy (inlet velocity of 0.1 mm/s)
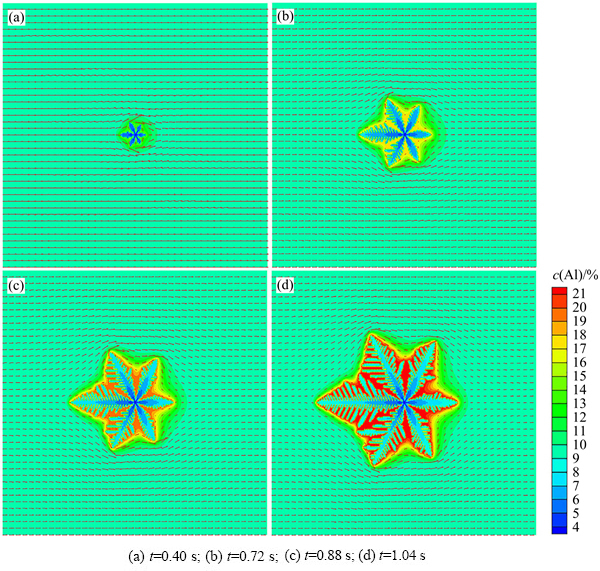
图2 模拟对流作用下不同时间AZ91镁合金单个等轴枝晶的生长
Fig. 2 Simulated single dendritic growth of AZ91 magnesium alloy with convection at different times
在其他条件不变时,改变入流速度,模拟不同入流速度对等轴晶枝晶形貌的影响如图4所示。由图4可知,随着入流速度的增大,迎流端枝晶生长越快。
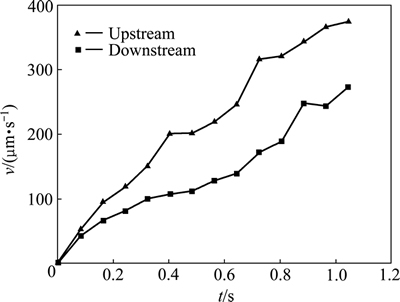
图3 AZ91镁合金枝晶尖端生长速率与凝固时间的关系
Fig. 3 Relationship between tip velocity of AZ91 magnesium alloy and solidification time
在背流端,入流速度较小时,背流端和朝右60°分支生长受到抑制,但仍有较小的二次臂生长(见图4(a));随着入流速度的增大,背流端和朝右60°分支变得细小(见图4(b)和(c));而当入流速度进一步增大时,朝右60°分支变得更为细小,生长受到很大抑制,从而使背流端分支形成较广阔的溶质扩散空间,使背流端分支又逐渐变大,并长出较大的二次枝晶臂(见图4(d))。此时,AZ91镁合金枝晶形貌较无对流时相差很大(见图1(a))。另外,从图4(d)也可看出,细小的朝右60°分支上方也有涡流出现,而较小的入流速度下并没有出现涡流。
为进一步分析入流速度对镁合金枝晶生长的影响,图5所示为不同入流速率下,枝晶迎流端(见图5(a))和背流端(见图5(b))前沿溶质元素含量距离枝晶尖端的分布情况。从图5中可以看出,与上述分析的变化趋势相对应,迎流端溶质梯度大,而背流端溶质梯度小。入流速度越大,迎流端溶质梯度越大,因此枝晶生长越快;而在背流端,入流速度越大,溶质梯度越小,从而枝晶生长越缓慢(见图4(d))。
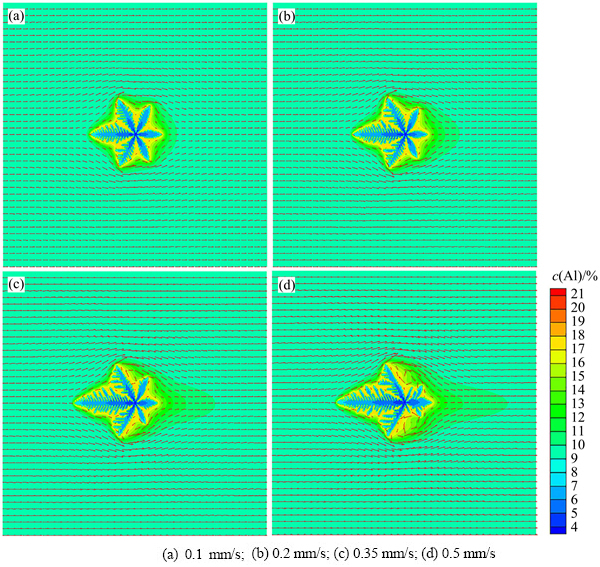
图4 不同入流速度下AZ91镁合金等轴枝晶生长模拟结果
Fig. 4 Simulated results of equiaxed dendritic growth of AZ91 magnesium alloy with different inlet velocities
3.2 对流作用下多个等轴枝晶的演变
在实际铸造条件下,凝固组织通常由不同取向的多个晶粒组成。图6所示为对流作用下具有不同取向的AZ91镁合金晶粒的演变过程。计算区域被划分成500 × 500个单元,网格步长为2 μm,将4个不同取向的核心种入区域,冷却速度为80 K/s,入流速度为0.2 mm/s。由图6(a)可以看出,在初始凝固阶段,各个枝晶独立生长,相互之间没有阻碍,在每个枝晶的周围可看到受对流作用影响而形成的不对称扩散层,扩散层在迎流端较窄,在背流端较宽,且随枝晶取向的变化而不同。随着凝固过程的进行(图6(b)~(d)),由于受流体冲刷影响,枝晶前端比后端生长粗大,且开始出现二次枝晶臂。模拟结果与文献[10]中模拟结果一致,与文献[28]中砂型AZ91D显微组织实验结果也十分相似。值得一提的是,对于不同取向的枝晶,受流体冲刷时,出现了不同的枝晶生长形态。图6所示的4个等轴枝晶的晶体取向分别为0°(左下)、15°(左上)、30°(右下)和45°(右上)。在迎流端最前沿的分支始终生长最粗大。对比左侧0°和15°取向枝晶,0°枝晶的最前沿分支(g0)呈现对称生长,g0的上部二次枝晶臂为t0;而15°枝晶的最前沿分支(g15)呈现非对称生长,g15的上部二次枝晶臂t15生长发达,枝晶臂较长,而下部二次晶臂b15生长较弱。对比二次晶臂t0和t15,发现t15比t0生长发达。主要原因是当枝晶分支生长方向与流体流向平行时(此时只代表迎流端的情况),主干迎流端受到流体冲刷作用最大,当枝晶分支方向与流体流向呈一定角度时,流体冲刷作用相对削弱,上述所说的t0与流体流向夹角大于t15与流体流向夹角,因此,t0生长弱于t15。
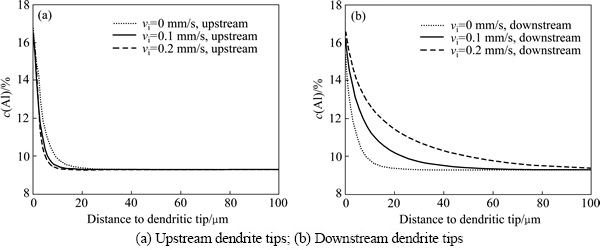
图5 不同入流速度迎流端和逆流端尖端AZ91镁合金中Al元素含量的变化
Fig. 5 Al concentration profiles of AZ91 magnesium alloy at upstream and downstream dendrite tips along horizontal direction with different velocities

图6 对流作用下不同时间具有不同取向的AZ91镁合金等轴晶生长的模拟结果
Fig. 6 Simulated results of equiaxed dendritic growth of AZ91 magnesium alloy with different crystal orientations and convection at different times
3.3 对流作用下定向凝固柱状枝晶的演变
柱状枝晶和等轴枝晶虽然有着同样的择优生长方向,但由于凝固前沿温度梯度、散热条件等的不同,柱状枝晶和等轴枝晶有着不同的生长形貌。依据对流作用下镁合金枝晶生长算法,模拟了对流对定向凝固柱状晶枝晶形貌和生长的影响。
图7所示为模拟得到的无对流和有对流作用时AM60镁合金柱状枝晶的生长形态。计算区域为300×500个单元,网格步长2 μm,定向凝固温度梯度为10 K/mm,方向沿垂直方向,初始时刻在计算区域底部放入4个形核核心,计算开始后,令计算区域以2.5 K/s的冷却速率进行冷却。为便于说明,在此将柱状晶从左到右依次编号为1、2、3、4号柱状晶。比较图7(a)和(b)可以发现,对流会对柱状枝晶的生长产生影响。由于左侧柱状晶的阻碍,只有受到溶质冲刷区域的枝晶生长比无对流时稍显粗大。对于3号柱状晶,左侧60°分支(l3)由于受到流体的冲刷比无对流时生长较长,且二次枝晶臂也相对较大。对比3号的右侧分支(r3)和4号的主分支,可以发现,由于r3生长相对减弱,使4号枝晶主干左侧二次枝晶臂具有足够的溶质扩散空间,进而促使4号枝晶主干左侧二次枝晶臂的生长。
图8所示为模拟得到的3个取向一致的柱状晶在对流作用下的演变过程。计算区域为200 × 500个单元,网格尺寸4 μm,其它条件与前述条件一致,并将3个柱状晶依次编号为5、6、7号柱状枝晶。虽然计算区域只有3个柱状晶,但3个晶粒之间间距较小,为了达到稳态,各个晶粒间要不断的协调竞争生长。由图8可以看出,6号晶粒在柱状晶的竞争生长中不断落后,最终5号和7号晶粒生长成粗大的柱状晶。同时,5号柱状晶二次枝晶臂l5在流体的冲刷下,不断长大,并在与周围二次枝晶臂的竞争生长中突显,最终长成和5、7号主干一样尺度的分支。此外,还可发现7号主干右侧二次晶臂比左侧发达,原因是由于左侧受到5号主干的竞争作用,生长受到阻碍,而右侧由于二次晶臂r7并未长成主干,溶质有较广阔的扩散空间,二次枝晶臂的生长不受枝晶的限制,所以生长较多也稍显粗大。相对于等轴枝晶受流体冲刷的结果,柱状枝晶的影响相对较小。从以上柱状晶受流体作用后的枝晶演变过程可以看出,虽然在等轴枝晶形貌上不同,但对于受到流体冲刷的枝晶臂,生长都较为粗大;不同的是,在柱状晶生长过程中,受靠近迎流端主干的阻碍和遮挡,流体冲刷给柱状枝晶的生长带来的影响会削弱,这与YUAN等[16]的结果一致。
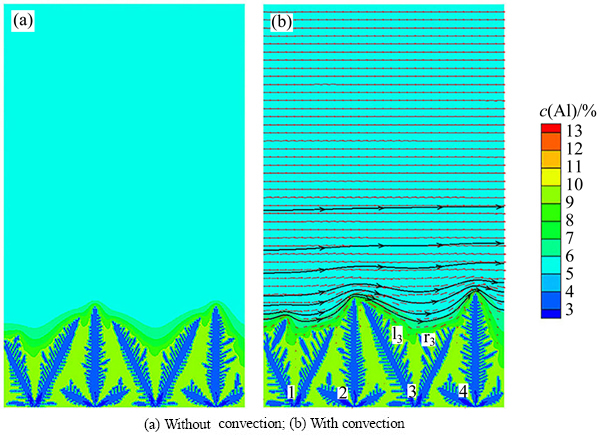
图7 时间为6.4 s时AM60镁合金柱状晶生长的模拟结果(入流速度为0.05 mm/s)
Fig. 7 Simulated results of columnar dendritic growth of AM60 magnesium alloy at 6.4 s (inlet velocity of 0.05 mm/s)
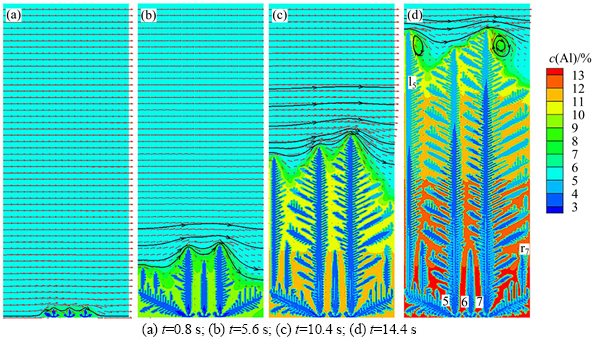
图8 对流作用下不同时间AM60镁合金柱状枝晶生长的模拟结果(温度梯度为10 K/mm,凝固速率为0.25 mm/s,入流速度为0.05 mm/s)
Fig. 8 Simulated results of columnar dendritic growth of AM60 magnesium alloy with convection (temperature gradient of 10 K/mm, solidification rate of 0.25 mm/s and inlet velocity of 0.05 mm/s)
4 结论
1) 将投影法求解流场过程与CA模型进行枝晶形貌模拟结合,模拟了对流作用下的镁合金即密排六方晶体结构等轴枝晶和定向凝固柱状枝晶形貌及其演变过程。
2) 模拟了对流作用下单个镁合金等轴枝晶的生长。枝晶在流体作用下,迎流端溶质浓度低,在背流端,溶质富集,从而迎流端尖端生长速率大于背流端,最终迎流端枝晶发达,二次枝晶臂亦较为发达,而背流端枝晶相比迎流端较为细小,镁合金枝晶呈现非对称生长。此外,不同入流速度下,在迎流端,入流速度越大,溶质梯度越大,枝晶生长越快;在背流端,入流速度越大,溶质梯度越小,枝晶生长越缓慢。
3) 实现了对流作用下多个具有不同取向的镁合金等轴枝晶的模拟。对流不仅影响等轴枝晶的形貌,也会影响扩散层的分布。不同取向等轴枝晶的扩散层会随着枝晶形貌的变化而变化,并在背流端呈现一定的拖曳特性。等轴枝晶分支方向与流体方向角度的不同,枝晶分支的形貌也会有不同;等轴枝晶分支方向与流体方向平行时,枝晶生长最发达;当有一定角度时,枝晶生长会相对削弱。
4) 模拟了对流作用下定向凝固柱状枝晶的演变过程。由于柱状枝晶的相互阻碍,迎流端较背流端的生长优势并不明显。模拟结果表明:对流在镁合金枝晶生长过程中起着重要作用。
REFERENCES
[1] MORDIKE B L, EBERT T. Magnesium: Properties- applications-potential[J]. Materials Science and Engineering A, 2001, 302(1): 37-45.
[2] KULEKCI M K. Magnesium and its alloys applications in automotive industry[J]. The International Journal of Advanced Manufacturing Technology, 2008, 39(9/10): 851-865.
[3] TONG X, BECKERMANN C, KARMA A, LI Q. Phase-field simulations of dendritic crystal growth in a forced flow[J]. Physical Review E, 2001, 63(6): 061601.
[4] LU Y, BECKERMANN C, RAMIREZ J C. Three-dimensional phase-field simulations of the effect of convection on free dendritic growth[J]. Journal of Crystal Growth, 2005, 280(1/2): 320-334.
[5] LAN C W, SHIH C J. Phase field simulation of non-isothermal free dendritic growth of a binary alloy in a forced flow[J]. Journal of Crystal Growth, 2004, 264(1/3): 472-482.
[6] STEINBACH I. Pattern formation in constrained dendritic growth with solutal buoyancy[J]. Acta Materialia, 2009, 57(9): 2640-2645.
[7] GUO Z, MI J, GRANT P S. Phase field simulation of multi-dendrite growth in a coupled thermal-solute-convective environment[C]// International Conference on Modeling of Casting, Welding and Advanced Solidification Processes-ⅩⅢ, MCWASP. UK: IOP Publishing, 2012: 012101.
[8] 袁训锋, 丁雨田, 郭廷彪, 胡 勇. 对流作用下枝晶生长行为的相场法[J]. 中国有色金属学报, 2010, 20(4): 681-687.
YUAN Xun-feng, DING Yu-tian, GUO Ting-biao, HU Yong. Phase-field method of dendritic growth under convection[J]. The Chinese Journal of Nonferrous Metals, 2010, 20(4): 681-687.
[9] 袁训锋, 丁雨田, 郭廷彪, 胡 勇. 强制对流作用下镁合金枝晶生长的相场法数值模拟[J]. 中国有色金属学报, 2010, 20(8): 1474-1480.
YUAN Xun-feng, DING Yu-tian, GUO Ting-biao, HU Yong. Numerical simulation of dendritic growth of magnesium alloys using phase-field method under forced flow[J]. The Chinese Journal of Nonferrous Metals, 2010, 20(8): 1474-1480.
[10] 尧军平, 李翔光, 龙文元, 张 磊. 镁合金不同取向多枝晶生长相场法模拟[J]. 中国有色金属学报, 2014, 24(2): 302-309.
YAO Jun-ping, LI Xiang-guang, LONG Wen-yuan, ZHANG Lei. Numerical simulation of multiple grains with different preferred growth orientation of magnesium alloys using phase-field method[J]. The Chinese Journal of Nonferrous Metals, 2014, 24(2): 302-309.
[11] ZHU M F, LEE S Y, HONG C P. Modified cellular automaton model for the prediction of dendritic growth with melt convection[J]. Physical Review E, 2004, 69(6): 061610.
[12] 朱鸣芳, 戴 挺, 李成允, 洪俊杓. 对流作用下枝晶生长行为的数值模拟[J]. 中国科学E辑, 2005, 35(7): 673-688.
ZHU Ming-fang, DAI Ting, LI Cheng-yun, HONG Jun-shao. Modelling of dendritic growth with convection[J]. Science in China Series E, 2005, 35(7): 673-688.
[13] 孙东科, 朱鸣芳. CA-LB 模型模拟对流枝晶生长[J]. 中国有色金属学报, 2007, 17(S1): s84-s89.
SUN Dong-ke, ZHU Ming-fang. Cellular automaton-lattice Boltzmann model for modeling of dendritic growth in flowing melt[J]. The Chinese Journal of Nonferrous Metals, 2007, 17(S1): s84-s89.
[14] SUN D, ZHU M, PAN S, RAABE D. Lattice Boltzmann modeling of dendritic growth in a forced melt convection[J]. Acta Materialia, 2009, 57(6): 1755-1767.
[15] YIN H, FELICELLI S D, WANG L. Simulation of a dendritic microstructure with the lattice Boltzmann and cellular automaton methods[J]. Acta Materialia, 2011, 59(8): 3124-3136.
[16] YUAN L, LEE P D. Dendritic solidification under natural and forced convection in binary alloys: 2D versus 3D simulation[J]. Modelling and Simulation in Materials Science and Engineering, 2010, 18(5): 055008.
[17] 石玉峰, 许庆彦, 柳百成. 对流作用下枝晶形貌演化的数值模拟和实验研究[J]. 物理学报, 2012, 60(12): 376-386.
SHI Yu-feng, XU Qing-yan, LIU Bai-cheng. Simulation and experimental research of melt convection on dendrite morphology evolution[J]. Acta Physica Sinica, 2012, 60(12): 376-386.
[18] 石玉峰, 许庆彦, 柳百成. 基于改进元胞自动机方法的强制对流作用下三维枝晶生长的数值模拟[J]. 稀有金属材料与工程, 2013, 42(4): 700-705.
SHI Yu-feng, XU Qing-yan, LIU Bai-cheng. Numerical simulation of 3-D dendritic growth under forced convection using the modified cellular automaton method[J]. Rare metal Materials and Engineering, 2013, 42(4): 700-705.
[19] 张显飞, 赵九洲. 对流作用下Al-Cu合金枝晶生长的数值模拟[J]. 特种铸造及有色合金, 2013, 33(4): 323-327.
ZHANG Xian-fei, ZHAO Jiu-zhou. Numerical simulation of the dendrite growth in Al-Cu alloy with melt convection by using cellular automaton model[J]. Special Casting & Nonferrous, 2013, 33(4): 323-327.
[20] 吴孟武, 熊守美. 基于改进CA方法的压铸镁合金微观组织模拟[J]. 金属学报, 2010, 46(12): 1534-1542.
WU Meng-wu, XIONG Shou-mei. Microstructure simulation of high pressure die cast magnesium alloy based on modified CA method[J]. Acta Metallurgica Sinica, 2010, 46(12): 1534-1542.
[21] NASTAC L. Numerical modeling of solidification morphologies and segregation patterns in cast dendritic alloys[J]. Acta Materialia, 1999, 47(17): 4253-4262.
[22] BELTRAN-SANCHEZ L, STEFANESCU D M. Growth of solutal dendrites: A cellular automaton model and its quantitative capabilities[J]. Metallurgical and Materials Transactions A, 2003, 34(2): 367-382.
[23] 吴孟武. 考虑压室预结晶及共晶组织的压铸镁合金微观组织模拟[D]. 北京: 清华大学, 2012.
WU Meng-wu. Microstructure simulation of die cast magnesium alloy considering the externally solidified crystals and eutectic phases[D]. Beijing: Tsinghua University, 2012.
[24] 田 政. 稀土添加及固溶处理对AM60镁合金组织及力学性能的影响[D]. 长春: 吉林大学, 2006.
TIAN Zheng. Research on influence of rear earth addition and solid solution treatment to the microstructure and mechanical properties of AM60 magnesium alloy[D]. Changchun: Jinlin University, 2006.
[25] 弭光宝, 何良菊, 李培杰, POPEL P S, ABATUROV I S. 添加少量钙的 AZ91D 镁合金熔体的黏度[J]. 中国有色金属学报, 2009, 19(8): 1372-1378.
MI Guang-bao, HE Liang-ju, LI Pei-jie, POPEL P S, ABATUROV I S. Viscosity of AZ91D magnesium alloy melt with small additions of calcium[J]. The Chinese Journal of Nonferrous Metals, 2009, 19(8): 1372-1378.
[26] AL-RAWAHI N, TRYGGVASON G. Numerical simulation of dendritic solidification with convection: two-dimensional geometry[J]. Journal of Computational Physics, 2002, 180(2): 471-496.
[27] KUMAR A. Isotropic finite-differences[J]. Journal of Computational Physics, 2004, 201(1): 109-118.
[28] 付振南, 许庆彦, 熊守美. 基于概率捕获模型的元胞自动机方法模拟镁合金枝晶生长过程[J]. 中国有色金属学报, 2007, 17(10): 1567-1573.
FU Zhen-nan, XU Qing-yan, XIONG Shou-mei. Numerical simulation on dendrite growth process of Mg alloy using cellular automaton method based on probability capturing model[J]. The Chinese Journal of Nonferrous Metals, 2007, 17(10): 1567-1573.
(编辑 王 超)
基金项目:国家自然科学基金资助项目(51275269);国家科技重大专项(2012ZX04012011);清华大学自主科研计划(20121087918)
收稿日期:2014-09-01;修订日期:2014-12-11
通信作者:郭志鹏,讲师,博士;电话:010-62789448;E-mail: zhipeng_guo@tsinghua.edu.cn