Trans. Nonferrous Met. Soc. China 28(2018) 1404-1412

Optimization of three-dimensional boiling enhancement structure at evaporation surface for high power light emitting diode

Jian-hua XIANG¹, Chao ZHOU¹, Chun-liang ZHANG¹, Gui-yun LIU¹, Cong-gui CHEN¹, Wei ZHOU²

1. School of Mechanical and Electric Engineering, Guangzhou University, Guangzhou 510006, China;

2. Department of Mechanical and Electrical Engineering, Xiamen University, Xiamen 361005, China

Received 28 January 2018; accepted 6 June 2018

Abstract: A theoretical model of phase change heat sink was established in terms of thermal resistance network. The influence of different parameters on the thermal resistance was analyzed and the crucial impact factors were determined. Subsequently, the forming methods including ploughing-extrusion and stamping method of boiling enhancement structure at evaporation surface were investigated, upon which three-dimensional microgroove structure was fabricated to improve the efficiency of evaporation. Moreover, the crucial parameters related to the fabrication of miniaturized phase change heat sink were optimized. The heat transfer performance of the heat sink was tested. Results show that the developed phase change heat sink has excellent heat transfer performance and is suitable for high power LED applications.

Key words: high power LED; phase change heat sink; ploughing-extrusion; boiling enhancement; three-dimensional microgroove

1 Introduction

Due to the limitations of materials, devices, circuits, system requirements etc, almost 85% of the energy from the light emitting diode (LED) chip power input is converted into heat [1,2]. Heat accumulation results in the rapid increase of junction temperature, thus causing a series of problems: (1) disastrous electrode slow or bad failure, (2) epoxy resin failure, (3) phosphor degradation failure, (4) color drift, (5) lower luminous efficiency, and (6) reduced service life. Thus, heat dissipation is the primary problem restricting the development of high power LED [3-6].

According to the research, more than 90% of the heat generated by the LED chip can only be dissipated by the encapsulating heat sink [7], and then to the surrounding environment through the external system radiator. Therefore, there is an urgent need of a kind of encapsulation-level heat transfer element suitable for the high heat flux of high-power LED. When the power of single LED (1 mm × 1 mm) reaches 2 or 3 W, its chip heat flux density is far more than the limit of air convection heat dissipation (100 W/cm²) of the aluminum/copper materials. Thus, the traditional metal solid heat sink with the air cooling methods has been unable to meet the requirements. On the other hand, phase change heat sink belongs to the gas/liquid cooling pattern, which has high thermal conductivity and excellent isothermal property, with a heat transfer coefficient up to 5 kW/(m²·°C). Therefore, phase change heat sink heat transfer device is a good choice for high power LED packaging, able to meet the demand of heat dissipation under high heat flow density conditions [3-6].

Much research activity has been directed to this field [8-14]. Representatively, JAJJA et al [15] investigated the influence of fin spacing onto microprocessors’ operating temperature. It was found that 0.2 mm fin spacing generated the lowest base temperature of 40.5 °C at a heater power of 325 W. HUANG et al [16] investigated thermal and fluid fields inside a LED lamp using numerical simulation. Upon the numerical model, they facilitated the determination of the optimal design of a LED lamp having 36 fins and an inner-shell thickness of 1 mm to increase heat dissipation. KIM et al [17] applied numerical simulation to seek the optimum thermal design of a heat sink consisting of a crevice-type vapor-chamber heat pipe in LEDs. They investigated the effects of the metal core printed circuit board (MCPCB) by virtue of the substrate thicknesses where the LEDs are mounted. Upon their study, a power of 40 W LED is applicable to a high-power package in a confined area. RAMOS-ALVARADO et al [18] evaluated the thermal performance of liquid active cooling devices that were fabricated on InGaN/sapphire chips to be used in high-power LED arrays. Full 3D numerical simulations were used to model mini-channel cold plates and micro-jets. It comes to a conclusion that the mini-channel cold plate is better than micro-jets for the cooling of high-power LEDs.

It is noted that the existing copper/aluminum heat sink is hard to meet the needs of high power LED heat dissipation. Therefore, a miniaturized phase change heat sink suitable for high power LED with a low thermal resistance and high heat transfer efficiency was developed, to adapt to high heat flux condition in the narrow space.

2 Theory analysis of phase change heat sink

2.1 Theoretical model

High-power LED phase change heat sink structurally belongs to the composite structure of soaking plates, as shown in Fig. 1(a). Accordingly, soaking slab theory can be applied to the analysis of thermal resistance of phase change heat sink. In order to simplify thermal resistance network of the phase change heat sink, the hypothesis is as follows: (1) The evaporation area is approximately equal to the heating area of the wick at the evaporation side, and there is no heat change between the cylindrical wall of the phase change heat sink and the outside, so heat is dissipated completely by the condensation side; (2) The wick at the evaporation side does not run dry, and the evaporation area is filled with liquid. On the basis of the above assumptions, the thermal resistance network of the phase change heat sink is shown in Fig. 1(b).

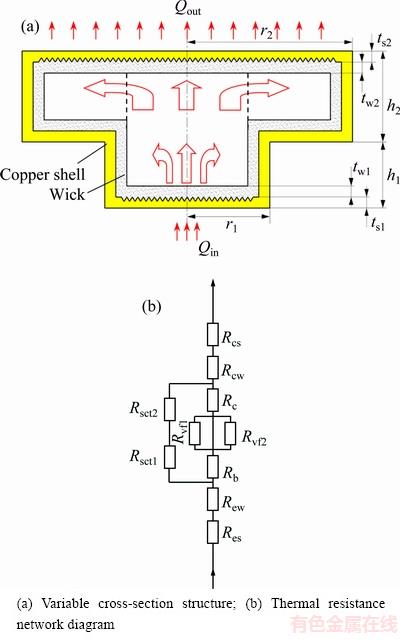
Fig. 1 Theoretical model of phase change heat sink

From the thermal resistance network, the thermal resistance of the phase change heat sink is as follows.

(1) The thermal conduction resistance of the solid metal at outer and inner surface of the evaporation side R_es:

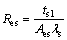                                 (1)

where the thickness of the solid metal at outer and inner surface of the evaporation side is t_s1, the thermal conductivity coefficient of solid metal is λ_s, and the heat transfer area of the evaporation side is A_es.

(2) The thermal conduction resistance of the wick at the evaporation side R_ew:

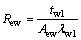                               (2)

where the thickness of the wick at the evaporation side is t_w1, the thermal conductivity coefficient of the wick is λ_w1, and the heat transfer area of the wick at the evaporation side is A_ew.

(3) The thermal convective boiling resistance at the evaporation side R_b:

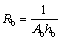                                 (3)

where the convective boiling heat transfer coefficient is h_b, and the boiling area of the evaporation side is A_b.

(4) The flow heat resistance of the steam under the small end of the heat sink R_vf1:

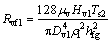                           (4)

where the dynamic viscosity of the steam is μ_v, the flow distance of the steam under small end diameter is H_v1, the diameter of the steam chamber at the small end is D_v1, the vapor density is ρ₁, and latent heat of vaporization is h_fg.

According to Clausius-Clapeyron equation, the temperature decrease of steam flow is

                              (5)

The pressure drop of steam loop is

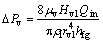                            (6)

where r_v1 is the radius of the steam chamber, and T_con is the temperature at the condensation end.

(5) The flow heat resistance of the steam under the big end of the heat sink R_vf2:

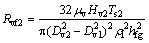                     (7)

where the flow distance of the steam under big end diameter is H_v2, and the diameter of the steam chamber at the big end is D_v2.

(6) The heat transfer resistance of the metal shell of the heat sink R_sct:

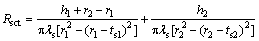    (8)

where the height of the outer wall at the small end is h₁, the height of the outer wall at the big end is h₂, the radius of the small end is r₁, the radius of the big end is r₂, the wall thickness of the small end is t_s1, and the wall thickness of the big end is t_s2.

(7) The convective heat resistance at the condensing side R_c:

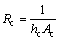                                  (9)

where the convective heat transfer coefficient at the condensing side is h_c, and the condensation area of the condensing side is A_c.

(8) The thermal conduction resistance of the wick at the condensing side R_cw:

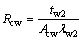                              (10)

where the thickness of the wick at the condensing side is t_w2, the thermal conductivity coefficient of the wick is λ_w2, and the heat transfer area of the wick at the condensing side is A_cw.

(9) The thermal conduction resistance of the solid metal at outer and inner surface of the condensing side R_cs:

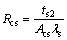                                (11)

where the thickness of the solid metal at outer and inner surface of the condensing side is t_s2, and the heat transfer area of the condensing side is A_cs.

According to the thermal resistance network diagram in Fig. 1(b), the total thermal resistance is

   (12)

2.2 Analysis of thermal resistance and structural parameters

According to Eqs. (1)-(10), the relationship between thermal resistance of phase change heat sink and the height of the small end and the big end can be obtained and exhibited in Fig. 2. With the increase of the height of h₁ and h₂, thermal resistance of phase change heat sink increases as well. From the perspective of the speed increase, thermal resistance of phase change heat sink increases faster with the increase of h₁ than that of h₂, showing that h₁ has larger influence on the thermal resistance of phase change heat sink. As phase change heat sink must meet basic packaging requirements, with the minimum total thermal resistance of phase change heat sink as the goal, h₁ should be chosen with smaller values, while h₂ with relatively large values if the total height is a constant.

Fig. 2 Relationship between height and thermal resistance of phase change heat sink

The proportion of thermal resistance of every part of the phase change heat sink to the total thermal resistance is compared. It is found that the thermal resistance of steam chamber dominates in the total thermal resistance of the phase change heat sink. Consequently, the proportion of thermal resistance of each part to total thermal resistance of vapor chamber is shown in Fig. 3.

It can be seen from Fig. 3 that the thermal convective boiling resistance at the evaporation side accounts for almost 93.70% of the total thermal resistance of steam chamber, and the convective heat resistance at the condensing side accounts for about 6.29% of the total thermal resistance of steam chamber. The sum of the two is very close to the total thermal resistance of steam chamber. Therefore, the thermal convective boiling resistance at the evaporation side dominates in the total thermal resistance. With the minimum thermal resistance as the design goal, it should be focused on lowering the thermal convective boiling resistance at the evaporation side. Thus, in the design of phase change heat sink, the enhanced boiling efficiency of the inner surface at the evaporation side should be improved, i.e., heat transfer performance of a phase change heat sink depends on the manufacturing of boiling enhancement structure at the evaporation side.

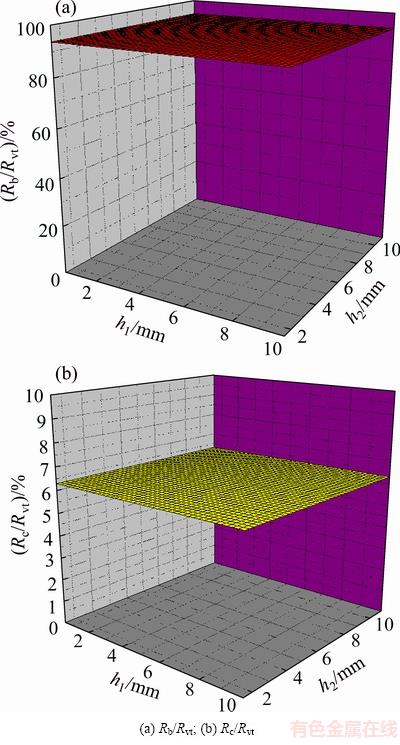
Fig. 3 Proportion of thermal resistance of each part to total thermal resistance (R_vt) of vapor chamber

3 Forming method of boiling enhancement structure at evaporation side

Boiling enhancement structure at the evaporation side is a kind of planar structure. However, the traditional planning forming method cannot be applied to machining the boiling structure at the bottom of the evaporation side. Accordingly, ploughing-extrusion and stamping methods with the assistance of special clamping were applied to machining three-dimensional boiling structures at the end face of the phase change heat sink. Firstly, spiral microgroove was machined at the circular plane of the evaporation side, as shown in Fig. 4(a). Secondly, radial microgroove was machined using the stamping forming method on the basis of the spiral microgroove, as shown in Fig. 4(b). Finally, three-dimensional microgroove was formed, where the radial and circumferential connect with each other within the plane of the evaporation side. This kind of microstructure can not only ensure the working substance circulation, but also enhance boiling, thus improving the performance of evaporation.

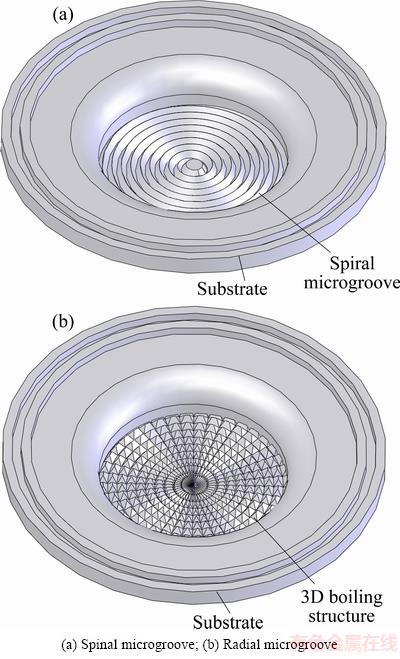
Fig. 4 Boiling enhancement structures at evaporation side

Spiral microgroove was machined using a common lathe specially clamped at the evaporation side. In the process of machining the boiling structure outside the pipe, the cutter was installed vertical to the axis of the work-piece and the direction of feed is in line with the direction of the axis of the work-piece. When it comes to the boiling structure at the evaporation side, the work-piece was fixed on the lathe chuck, and the cutter was installed parallel to the axis of the work-piece. The direction of feed is along the direction of the diameter of the work-piece. In the process of the rotary motion of spindle, a constant feeding was maintained, and in such a way, spiral microgroove was machined at the inner surface of the evaporation side.

Stamping method was applied to the formation of radial microgroove at the bottom of the evaporation side. The work-piece is fixed on the rotating disk, and the direction of the stamping cutter is in line with the direction of the axis of the work-piece, where the cutting tool reciprocates up and down. After the determination of the stamping depth, the cutting tool moves downwards to stamp the work-piece, forming a radial microgroove. After that, the cutting tool moves upwards and at the same time the rotating disk is rotated by a certain angle. Subsequently, the cutting tool moves down again to form another microgroove. The included angle between these two microgrooves is equal to the rotated angle of the rotating disk. Repeating the former steps until the entire plane is processed, the radial microgroove boiling structure can be formed with the center of the work-piece being the origin. This kind of structure is advantageous to the liquid flow from the radius to the centre of the evaporating surface.

4 Results and discussion

4.1 Effect of ploughing-extrusion feedings on morphology of microgrooves

Experimental study was conducted with different feedings f_h and ploughing-extrusion depths a_ph using a blade having a main extrusion angle of r₀=30°, auxiliary extrusion angle of r'₀=10°, main shaping angle of β=15°, and auxiliary shaping angle of β'=5°. The experimental results are shown in Fig. 5. According to the experiment, the helix distance d_ph depends on the feeding f_h, i.e., there is a proportional relationship between the two. If there is a small feeding, the helix distance will be small as well.

Figure 5 shows the morphologies of microgrooves with different d_ph when a_ph=0.3 mm. In the case of d_ph=0.5 mm, the height of the fin is 0.27 mm, as shown in Fig. 5(a). It is found that the height of the fin increases with the increase of d_ph when d_ph is relatively small. This is due to the effect of extrusion and trim during the formation of the microgrooves. With the increase of d_ph, part of the metal flow is higher than primitive plane due to the extrusion to the bottom of the microgrooves, resulting in the formation of sharp-shaped fin at the top.

With the further increase of d_ph, auxiliary grooves are formed due to the accumulation of the metal extruded to the edge of microgrooves. When d_ph=1.5 mm, the height of the fin reaches a maximum value of 0.59 mm, as shown in Fig. 5(b). The height of the fin does not further increase due to the fact that there is no extrusion or trim to the fin when d_ph is larger than 1.5 mm, i.e., there is no interference between microgrooves and fins. When d_ph=1.96 mm, the height of the fin is 0.54 mm, as shown in Fig. 5(c). According to the experiment, the width of the auxiliary grooves increases with the increase of d_ph.

Fig. 5 SEM images of circumferential grooves under different feedings

It can be observed that, the height of the fin increases with the increase of feeding when d_ph is relatively small. When d_ph increases to a critical value, the height of the fin gets to the maximum. And then, with the further increase of d_ph, the height of the fin decreases slowly. The relationship between the height of the fin and the helix distance of the ploughing-extrusion is shown in Fig. 6. Consequently, when performing the ploughing- extrusion, there exist different optimal values in terms of different ploughing-extrusion depths, which can be determined by similar experiments as above.

4.2 Effect of ploughing-extrusion depths on morphology of microgrooves

The morphology of microgrooves is not only influenced by f_h, but also influenced by a_ph. The morphologies of microgrooves with different a_ph are shown in Fig. 7, with d_ph as a constant of 0.5 mm. It can be seen that the depth of the microgroove increases with the increase of a_ph. The residual metal between the grooves starts to yield due to the extrusion of the auxiliary extrusion surface A′_γ and the trim of the auxiliary forming surface A′_β, and then bends towards the normal direction of the auxiliary forming surface A′_β.

Fig. 6 Relationship between helix distance of ploughing- extrusion and height of fin

The height of the fin is 0.2 mm as a_ph is equal to 0.1 mm, as shown in Fig. 7(a). During the formation of microgrooves, there is not interference between two adjacent grooves as the feeding is larger than a_ph, making the height of the fin larger than the ploughing-extrusion depth a_ph. When a_ph is increased to 0.3 mm, the height of the fin is 0.27 mm, which is due to the fact that the deformation zones of two adjacent grooves contact with each other, making the decrease of the height of the fin resulted from the trim effect, as shown in Fig. 7(b). It can be observed that the width of the microgroove is narrowed due to the trim of the auxiliary forming surface. Thus, the ratio of depth to width is increased, making the ability to store liquids and gases increase as well, which is beneficial to the boiling of the working fluid. When a_ph is further increased to 0.5 mm, the height of the fin is 0.43 mm due to the effect of trim, and a large number of flashes are generated as the feeding is too small, as shown in Fig. 7(c).

The ratio of the height of the fin to the ploughing-extrusion depth with a constant helix distance of 0.5 mm is shown in Fig. 8. It can be seen that the height of the fin increases with the increase of the ploughing-extrusion depth, but in contrast, the ratio of the height of the fin to the ploughing-extrusion depth tends to decrease. This is due to the fact that, with the increase of the height of the fin, the effect of trim is strengthened. Therefore, both the ploughing-extrusion depth and the feeding have a great impact onto the formation of microgrooves.

Fig. 7 SEM images of circumferential grooves under different a_ph

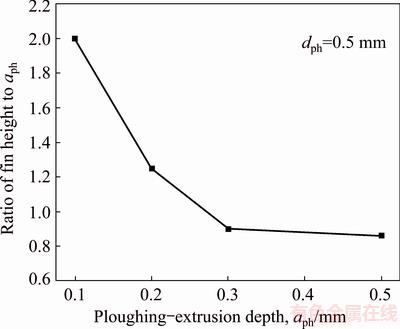
Fig. 8 Ratio of height of fin to ploughing-extrusion depth

4.3 Effect of velocity of ploughing-extrusion

According to the ploughing-extrusion process, the cutting speed changes continuously with the approaching of the cutting tool from the outer diameter to the center of the work-piece. The cutting speed is the largest at the outer diameter of the work-piece. With the approach to the centre of the work-piece, the cutting speed is gradually reduced, resulting in a possible bonding of the copper with the cutting tool. Therefore, the spindle speed should not be too low, with 50-100 r/min advisable.

In the process of the ploughing-extrusion, d_ph and a_ph have a decisive role in the formation of microgrooves. Assume that the thread pitch depth and the ploughing-extrusion depth at the critical point of pruning are d_pcv and a_pcv, respectively, and the minimum spindle speed without adhesive failure is n_msv:

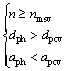                                (13)

With the conditions in Eq. (13) satisfied, there is no interference during the formation of microgrooves, and the height of the fin is consistent with the height of a single groove fin, resulting in a composite structure made up of V grooves and U grooves.

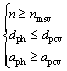                                (14)

With the conditions in Eq. (14) satisfied, there exists interference during the formation of microgrooves, resulting in a single structure made up of V grooves. The height of the fin decreases due to the trim effect, and flashes are generated, even resulting in a substantial accumulation of metal unable to be processed.

n＜N_msv                                     (15)

With Eq. (15) satisfied, irregular burrs are produced, and microgrooves cannot be formed.

4.4 Effect of stamping depth on morphology of microgrooves

The morphologies of microgrooves with different stamping depths are shown in Fig. 9. Figure 9(a) shows the morphology of microgrooves with a stamping depth (a_c) of 0.2 mm and a spacing (d_c) of 0.4 mm, where there is no interference between grooves. Figure 9(b) shows the morphology of microgrooves with a stamping depth of 0.3 mm and a spacing of 0.4 mm. It can be observed that the formation of the current groove has an impact on the previous groove. This is due to the fact that, with the increase of the stamping depth, the thickness of the metal between the grooves decreases, making the metal tilt towards the direction of the previous groove under the extrusion of the cutting blade, resulting in an increase of the depth-to-width ratio since the width of the previous groove decreases. When the stamping depth is increased to 0.5 mm, and the spacing is increased to 1.0 mm, the morphology of grooves keeps consistent with a single groove, as shown in Fig. 9(c). Thus, it can be seen that the morphology of grooves is determined by the stamping depth and the stamping spacing.

Fig. 9 SEM images of V grooves under different stamping depths and spacings

4.5 Mutual effect between spiral grooves and radial grooves

When the ploughing-extrusion parameters meet Eq. (12), the circumferential spiral structure is made up of top-sharp V grooves, and after stamping, the optimized three-dimensional boiling enhancement structure is formed, as shown in Fig. 10. If Eq. (12) is satisfied, three-dimensional finned structures with obvious bending are formed when d_ph gets larger, and this kind of structure is the optimal fin structure.

Fig. 10 Three dimensional boiling structures with sharp fins

4.6 Heat transfer performance testing of developed phase change heat sink

The heat sink testing platform was developed, as shown in Fig. 11. The heat transfer performance of the phase change heat sink with different input powers was tested. The test results using pure water as the working fluid under heat load of 3 and 5 W are shown in Fig. 12. It is seen that temperature increases with the increase of input power. When input power is 3 W, the time duration to reach system balance takes about 60 min. The highest temperature is 39.2 °C. When the input heat power rises to 5 W, the time to reach the balance is about 48 min. The highest temperature is 54.7 °C. To make a comparison, heat transfer performance of metal solid heat sink was tested. Under the input power of 3 W, the balance temperature of the metal solid heat sink is up to 68.2 °C, as shown in Fig. 13(a). When the input power is further increased to 5 W, the maximum temperature reaches 101.7 °C, as shown in Fig. 13(b). Therefore, the developed phase change heat sink has much better heat transfer performance than traditional metal solid heat sink.

Fig. 11 Heat sink testing platform

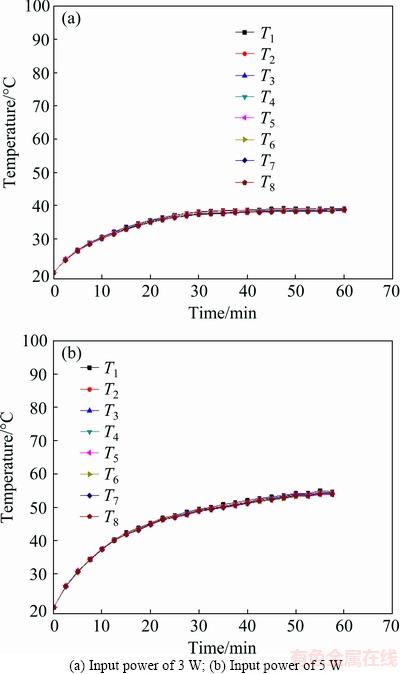
Fig. 12 Heat transfer performance of phase change heat sink

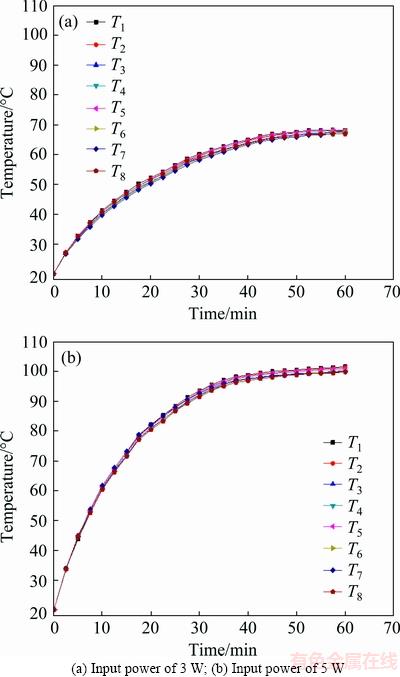
Fig. 13 Heat transfer performance of metal solid heat sink

5 Conclusions

1) A theoretical model of phase change heat sink in terms of thermal resistance network was proposed, upon which the influence of different parameters on the thermal resistance was analyzed and the crucial impact factors were determined.

2) The forming methods of boiling enhancement structure in evaporation surface were investigated including ploughing-extrusion and stamping method, upon which three-dimensional microgrooves structure was machined to improve the efficiency of evaporation.

3) Crucial parameters related to manufacturing of miniaturized phase change heat sink were analyzed and optimized.

4) Heat transfer performance of the developed phase change heat sink was tested and compared with that of solid metal heat sink. The results show that the developed heat sink has excellent heat transfer performance and is suitable for high power LED applications.

References

[1] YUNG K C, LIEM H, CHOY H S, CAI Z X. Thermal investigation of a high brightness LED array package assembly for various placement algorithms [J]. Applied Thermal Engineering, 2014, 63(1): 105-118.

[2] NARENDRAN N, GU Y, FREYSSINIER J P, YU H, DENG L. Solid-state lighting: Failure analysis of white LEDs [J]. Journal of Crystal Growth, 2004, 268(3-4): 449-456.

[3] LUO X, HU R, LIU S, WANG K. Heat and fluid flow in high-power LED packaging and applications [J]. Progress in Energy and Combustion Science, 2016, 56: 1-32.

[4] REMELLA K S, GERNER F M. Simplified mathematical model of a novel ‘closed loop two-phase wicked thermosyphon (CLTPWT)’ [J]. International Journal of Thermal Sciences, 2017, 114: 281-295.

[5] TSAI M Y, CHEN C H, KANG C S. Thermal measurements and analyses of low-cost high-power LED packages and their modules [J]. Microelectronics Reliability, 2012, 52(5): 845-854.

[6] CHUNG C H, YANG K S, CHIEN K H, JENG M S, LEE M T. Heat transfer characteristics in high power LED packaging [J]. Smart Science, 2014, 2(1): 1-6.

[7] ADAM C, SAMUEL G. Thermal effects in packaging high power light emitting diode arrays [J]. Applied Thermal Engineering, 2009, 29(2-3): 364-371.

[8] ZHAO T, CHEN R. Recent progress in understanding of coupled heat/mass transport and electrochemical reactions in fuel cells [J]. International Journal of Energy Research, 2011, 35(1): 15-23.

[9] ALI H M, ARSHAD W. Effect of channel angle of pin-fin heat sink on heat transfer performance using water based graphene nanoplatelets nanofluids [J]. International Journal of Heat & Mass Transfer, 2017, 106: 465-472.

[10] ARSHAD W, ALI H M. Experimental investigation of heat transfer and pressure drop in a straight minichannel heat sink using TiO₂ nanofluid [J]. International Journal of Heat & Mass Transfer, 2017, 110: 248-256.

[11] XIANG J, ZHANG C, JIANG F, LIU X, TANG Y. Fabrication and testing of phase change heat sink for high power LED [J]. Transactions of Nonferrous Metals Society of China, 2011, 21(9): 2066-2071.

[12] XIANG J, DUAN J, ZHOU H, ZHANG C, LIU G, ZHOU C. Forming mechanism of three-dimensional integral fin based on flat surface [J]. Journal of Central South University, 2015, 22(5): 1660-1666.

[13] ALI H M, ARSHAD W. Thermal performance investigation of staggered and inline pin fin heat sinks using water based rutile and anatase TiO₂ nanofluids [J]. Energy Conversion & Management, 2015, 106: 793-803.

[14] ALI H M, GENEROUS M M, AHMAD F, IRFAN M. Experimental investigation of nucleate pool boiling heat transfer enhancement of TiO₂-water based nanofluids [J]. Applied Thermal Engineering, 2017, 113: 1146-1151.

[15] JAJJA S A, ALI W, ALI H M, ALI A M. Water cooled minichannel heat sinks for microprocessor cooling: Effect of fin spacing [J]. Applied Thermal Engineering, 2014, 64(1-2): 76-82.

[16] HUANG D S, LIAO Y S, KUO H J, KUO F J, LIN M T. Simulation of a high-power LED lamp for the evaluation and design of heat dissipation mechanisms [J]. Microsystem Technologies, 2016, 22(3): 523-529.

[17] KIM J S, KIM E P. Analysis of the thermal management of a high power LED package with a heat pipe [J]. Journal of the Korean Society of Marine Engineering, 2016, 40(2): 96-101.

[18] RAMOS-ALVARADO B, FENG B, PETERSON G P. Comparison and optimization of single-phase liquid cooling devices for the heat dissipation of high-power LED arrays [J]. Applied Thermal Engineering, 2013, 59(1-2): 648-659.

大功率LED蒸发面三维强化沸腾结构优化

向建化¹，周 超¹，张春良¹，刘贵云¹，陈从桂¹，周 伟²

1. 广州大学 机械与电气工程学院，广州 510006；2. 厦门大学 机械与电气工程学院，厦门 361005

摘  要：利用热阻网络方法建立相变热沉理论模型，分析各参数对相变热沉热阻的影响，并确定影响热阻的主要因素。利用冲压挤压法在相变热沉蒸发面成形三维微沟槽强化沸腾结构以提高蒸发效率，并优化小型相变热沉制造的关键参数。另外，基于开发的测试平台对相变热沉的传热性能进行测试。测试结果表明，该相变热沉具有良好的传热性能，适用于大功率LED的散热。

关键词：大功率LED；相变热沉；冲压挤压法；强化沸腾；三维微沟槽

(Edited by Bing YANG)

Foundation item: Projects (51575115, 51775122) supported by the National Natural Science Foundation of China

Corresponding author: Jian-hua XIANG; Tel/Fax: +86-20-39366923; E-mail: xiangjh@gzhu.edu.cn

DOI: 10.1016/S1003-6326(18)64779-X