轴流式喷水推进泵的三元设计

彭云龙，王永生，靳栓宝

(海军工程大学 动力工程学院，湖北 武汉，430033)

摘要：运用泵的三元设计理论和计算流体力学(CFD)数值计算方法对大功率、高效率轴流式喷水推进泵进行水力设计和性能预报，并对喷口轴向长度、叶轮叶片随边与导叶叶片导边的轴向距离以及叶顶间隙对喷泵水力性能的影响进行进一步计算与分析。从理论上说明叶轮叶片和导叶叶片之间存在最佳匹配距离，该最佳间距为标称直径的3%~4%。运用黏性雷诺时均方法(RANS)对所设计轴流式喷泵水力性能进行数值预报。研究结果表明：泵在设计流量点效率达到92.3%，同时也满足抗空化性能要求，且在较宽的流量范围内具有良好的水力性能。

关键词：喷水推进；轴流泵；三元反向设计；计算流体力学

中图分类号：U664.33          文献标志码：A         文章编号：1672-7207(2014)06-1812-07

Three-dimensional inverse design method applied to waterjet axial-flow pump

PENG Yunlong, WANG Yongsheng, JIN Shuanbao

(College of Marine Power Engineering, Naval University of Engineering, Wuhan 430033, China)

Abstract: A large power and high efficiency axial-flow waterjet pump was designed by the three-dimensional inverse design method, whose performance was predicted by CFD. The influences of the length of nozzle, the axial distance between a rotor’s trailing edge and a stator’s leading edge, and the clearance of rotor blade tip on pump’s hydraulic performance, were studied in the design process. The results show that there must be an optimized distance in theory and the best one in this example is 3%-4% of the pump’s inlet diameter. The result of this research provides a reference for the waterjet pump designers. Then, the performance of the axial-pump is calculated using RANS simulation, which indicates the pump has good cavitation and high efficiency with 92.3% at the design point.

Key words: waterjet; axial-pump; three-dimensional inverse design method; computational fluid dynamics (CFD)

喷水推进是利用喷水推进泵射流反作用力推动船舶前进，它具有高航速时推进效率高、抗空化性能好、水下辐射噪声低、船舶操纵性和机动性能优等诸多常规螺旋桨所不能比拟的特点，并依托这些优良特性在高速高性能船舶领域得到广泛应用^[1-3]。喷水推进泵是喷水推进器的核心部件，它首先根据船舶类型、阻力大、主机类型等因素来选型，并依据所得选型参数进行喷泵的水力设计和强度设计。船用喷泵有效率高、流量扬程系数大、抗空化能力强、强载度高、结构紧凑等设计要求，故喷泵的设计难度较陆用普通泵大许多^[4-5]。因此，采用传统的一元、二元方法优质完成对进流条件复杂的喷泵的水力设计是非常困难的。运用减少条件假设、更接近实际泵体内部流动规律的三元设计方法设计喷泵叶片是泵现代设计方法发展的必然选择。近年来，计算流体力学(CFD)已越来越多应用于喷水推进器的性能分析和优化设计。Allison等^[4] 介绍了耦合叶轮升力面理论和轴对称的RANS方程来设计喷水推进泵。Gao等^[6]用CFD手段分析了轴流式喷水推进泵叶轮和导叶体内流场特性分析结果并与试验结果基本吻合。靳栓宝等^[7]提出了基于数值试验的喷水推进泵一体化设计，然后运用CFD 方法进行验证优化。国外的许多喷水推进厂商如Wartsila，KaMeWa，MJP和Hamilton公司也都将计算流体力学应用于设计新型喷水推进器过程。本文作者研究采用三元反问题方法对某大型双体穿浪船轴流式喷水推进泵进行设计，研究喷口长度、叶轮与导叶叶片轴向间距和叶轮叶顶间隙对泵水力性能的影响，得到相应的最优值，并通过三维考虑流体黏性的雷诺时均方法(RANS)对所设计泵进行数值预报，验证三元设计方法的可行性、先进性，同时也为泵的设计者提供部分设计参考值。

1  三元设计的数学模型

假设泵内部流动是无黏性、不可压缩流动，叶轮的进流是无旋的并且不考虑叶片厚度，这样叶片就可以用涡片(sheets of vorticity)代替。涡片的强度由周向平均旋转速度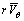决定，其与边界环量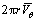直接相关^[8-9]。定义如下：

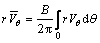             (1)

其中：r为径向坐标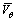；为周向速度平均值；θ为周向转角；B为叶片数。叶轮内流场的旋度为

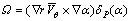           (2)

其中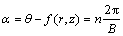：，是一个标量函数，表示叶片表面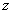；为轴向坐标；θ为周向转角；f(r，z)为叶片上的角坐标，也称为包角；n为整数0，±1，±2，…；梯度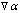即是叶片表面的法向矢量；δ_P(α)为一个平均值为1的周期函数，当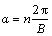时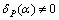，，其余都为0。所以平均旋度为^[9]

             (3)

首先运用二元理论估算出在该流量、轴面形状和转速下的轴面速度分布并通过壁面条件得到初始叶片形状，壁面无滑移边界条件数学式^{[8, 10]}：

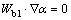               (4)

式中：为叶片表面法向量；W_b1为叶片表面相对速度(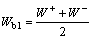，其中W⁺为叶片上表面速度，W^-为叶片下表面速度) 即而上式可扩展为：

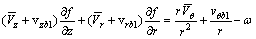  (5)

式中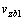：为周期叶片表面轴向速度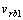；为周期叶片表面径向速度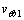；为周期叶片表面周向速度；f为叶片包角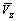；为轴向速度平均值；ω为叶轮的转动角速度。可以看出：式(5)为一阶双曲线偏微分方程，其特征线恰好是叶片流线的轴面投影，叶片的初始形状需沿轴线积分来求取。

获得叶片的初始形状后，利用式(2)可求得叶片表面的涡分布，进而可以重新计算叶轮的三维速度场。三元设计理论是将泵内部速度流场耦解为周向平均流动和周向脉动两部分。周向平均流动直接由三维Euler方程组作周向平均导出，周向脉动流动由连续方程通过Clebsch变换建立起控制方程^[11]，用置于叶片中心面上的源汇来代替叶片厚度对流场的作用。整个流场的流动通过计算周向平均流动二维泊松方程来求解，周期流场中的周期流动变量用傅里叶级数沿周向展开，把一个三维问题转化为无穷多个二维平面问题来求解(实际计算时只取有限项即可)。然后用有限差分法和贴体坐标系求解整个速度流场。求取叶轮新速度场以后，通过式(4)可以再次求取叶片的形状，对初始叶片形状进行修正优化，因此整个设计过程是一个迭代过程。

此外，流场数学模型的求解也要满足Kutta-Joukowski条件，即叶片随边处上下表面静压力要相等^[10-11]。文献推导出叶片上下表面速度跳跃：

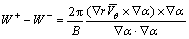       (6)

沿流线用无黏性的伯努利方程对上式简化得到叶片上下表面压力差(上表面压力为p⁺，下表面压力为p^-)为：

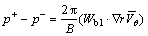          (7)

进而可以得出满足库塔条件的要求为

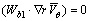              (8)

2  喷水推进泵水力设计

以某大型双体穿浪船为对象进行轴流式喷水推进泵选型后，根据选型所得设计参数开展喷泵水力设计。

2.1  轴面投影图的确定

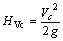喷泵轴面过流通道对泵的过流能力、水力效率和空化性能都有重要影响^[12]。本研究参考国内外优秀水力模型，以内切流线法为指导，考虑实际装船后的几何尺寸约束绘制该喷泵的轴面投影图(图1)。喷口作为喷水推进泵的出流部件，它对喷泵水力性能有直接影响，文中对3个不同轴向长度的喷口进行对比性计算，从中选择合适的喷口长度，结果见表1。这里定义无量纲参数c用来分析喷口出流截面流体非轴向能量在总能量中所占比例，c越小表明喷口整流效果越好。，喷口截面处周向速度压头为，轴向速度压头为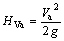，径向速度压头为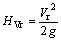，总压头。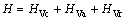

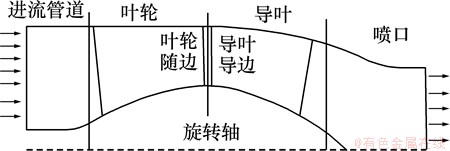
图1  喷泵轴面形状

Fig. 1  Meridional geometry of the waterjet

表1  不同喷口泵的性能归一化对比

Table 1  Comparison of different nozzles

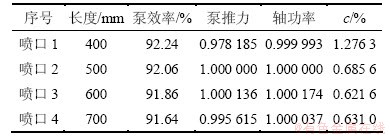
由表1可知：随着喷口轴向长度的增加，流体与喷口壁面摩擦损失增加，喷泵效率呈下降趋势，泵产生推力会在这个过程中存在一个最大值，文中喷对应喷口3，此时泵轴功率达到最大值，喷口出流截面c为最小，这说明喷口并非越长或越短越好。喷水推进泵以产生轴向推力推动船舶前进为目的，对比以上四个喷口，喷口2和3轴向推力、功率和c变化不大，且喷口2对应喷泵效率较高，所以，选择500 mm为设计喷口长度如图1所示，约为叶轮进口直径的40%。

2.2  喷泵叶片负载分布规律

叶片的负载(即叶片压力面和吸力面的压力差)分布对叶片的形状、扭曲程度和流体的流动特性有直接影响，合理的负载分布是喷泵高效的必要条件。叶片数越多，单个叶片承载负荷越小，但叶片表面的摩擦损失增加。权衡考虑本文设计喷泵叶轮叶片数为6片，导叶叶片数为11片。参考文献[13-14]，叶轮采用的是前重载型负载分布，叶片负载逐渐增加，大约在20%弦长处达到最大值，平缓过渡在40%弦长处开始下降。这种负载分布使得叶轮叶片在吸力面压力先是增加，然后缓慢变化至根部，这可以减小尾部边界层分离的发生，同时适当的保持一定范围的最大负载也可以减小低压区面积改善叶片的抗空化性能，叶轮轮毂和外壳截面的负载分布如图2所示。

导叶的作用主要是对喷水推进泵叶轮出流整流，保证喷水推进泵出流无旋转分量，以提供最大的轴向推力。导叶负载分布规律参考优化叶轮叶片负载分布，如图3所示。叶片负载在叶顶截面和叶根截面已给定，其他截面利用线性插值的方法求得，这样可以求得整个轴面的负载分布。

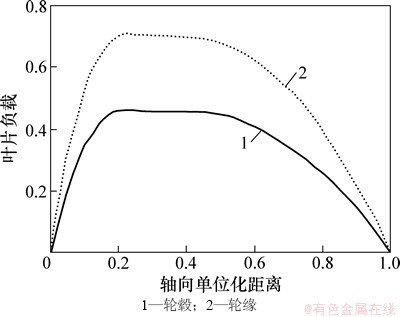
图2  叶轮负载分布

Fig. 2  Blade loading distribution of the rotor

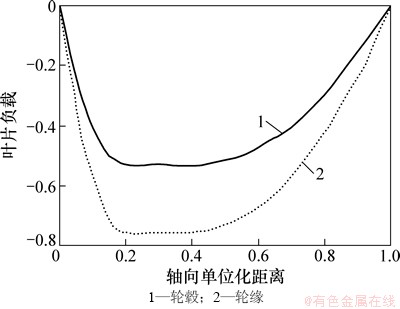
图3  导叶负载分布

Fig. 3  Blade loading distribution of the stator

2.3  叶片加厚

经计算得到叶片无厚度中心面后，采用NACA翼型系列厚度分布规律，在保证叶片强度前提下对叶轮和导叶叶片进行加厚，生成三维几何。泵最终设计几何结构如图4所示。

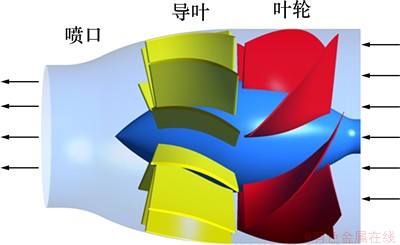
图4  轴流式喷水推进泵几何

Fig. 4  Geometry of axial-flow pump

2.4  叶片轴向距离对性能影响

叶轮叶片和导叶叶片是流场相互作用、相互影响的水力做功部件。水流由叶轮随边流出进入导叶导边(图1)。水流在进入叶轮叶片后按叶轮叶片形状接受叶轮做功，流出后又经导叶叶片整流由喷口喷出。此时叶轮随边与导叶导边轴向距离影响到流体在叶轮叶片的出流角与导叶叶片的进流角是否合理匹配，距离偏小或过大都不是合理的匹配关系。若距离偏小会致使导叶叶片进流紊乱，泵内部流场脉动力较大，影响导叶的整流效果降低喷泵产生推力，缩短泵的使用寿命；若距离较大又会造成导叶进流角过小，在叶片工作面产生脱流出现漩涡，能量损失增大，泵本身不能有效地发挥出相应的做功能力^[15]。

本文在叶片负载分布、叶片轴向长度、叶片厚度、安放角以及叶轮旋转域等因素不变的条件下，保证叶轮叶片和导叶叶片轴向距离单一变量，研究了5种不同轴向距离对泵水力性能的影响，得出最优的轴向距离，为轴流式喷水推进泵的设计参数选取提供参考。结果见图5和图6，这里坐标轴上数值1表示设计流量下的对应值，图中显示为归一化处理后结果。

由图6可知：轴向距离偏小会使低流量时泵内部流场流动顺畅，最高效率点向低流量方向偏移，小间距的直接结果是叶轮和导叶的干涉影响加大，这引起喷泵消耗轴功率也增大。在轴向距离增加的过程中，泵效率曲线逐步升高达到一个较高水平然后下降，当间距再次加大时效率曲线又会反弹升高，这是因为当轴向间距增大到一定值时叶轮导叶之间干涉引起的流动损失大大减小，其效果大于导叶进流角减小对流动产生的影响，整体损失降低。在间距增大期间会存在一个相对最优间距，当处于最优间距时(文中对应48.3 mm)，叶轮叶片出流角与导叶叶片进流角匹配最佳，流体从叶轮流出后可以在最小流动损失的情况下进入导叶体，此时泵的整体水力效率较高，轴功率消耗较低，流体压力脉动较小，整个泵体结构也较为紧凑，综合指标较高。该型轴流喷水推进泵实际工作中受船舶航速影响要求要有较宽的高效区域，是高效、紧凑型喷泵。这里选用最佳轴向间距为48.3 mm，最高效率为92.3%。 根据以上研究分析，作者认为此型轴流式喷泵叶轮叶片随边与导叶叶片导边的最佳轴向间距为喷泵进口直径的3%~4%。

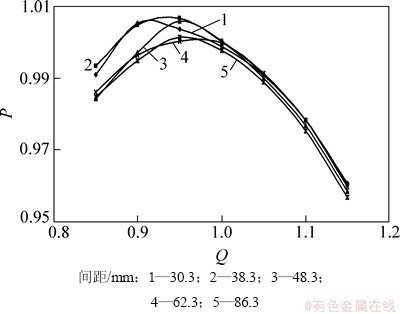
图5  不同间距时喷泵轴功率归一化对比

Fig. 5  Shaft power comparison of different distances

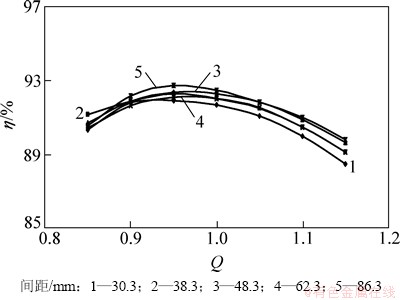
图6  不同间距时喷泵效率对比

Fig. 6  Efficiency comparison of different distances

2.5  叶顶间隙对性能影响

叶顶间隙是指叶轮叶片顶端与叶轮外壳之间的轴向间隙。往往在泵的安装和工作过程中，受回转力矩等因素的影响叶轮的叶顶间隙会发生变化，对此作者对比分析了5种不同叶顶间隙(s=1.3，1.5，1.8，2.1，2.5 mm)下泵的水力性能。计算所得的性能曲线如图7所示。从图7可以看出：随着叶顶间隙的增大，泵的扬程、功率和效率都会逐渐减小。这是因为叶顶处压力面与吸力面的压差会导致叶顶间隙处形成泄流，泄流不仅会减少做功流体体积，而且会与主流发生卷吸作用增大损失,此外较长的泄流尾迹作用在相邻叶片上还会增大临近叶片叶稍空化风险。较小叶顶间隙在减小泄流提高喷泵效率的同时，也会引起泵壳体脉动增大，不利于现在轴流式喷水推进泵低噪声、高转速的设计要求。所以，要选取和保持合适的叶顶间隙，此型泵取中间值1.8 mm。

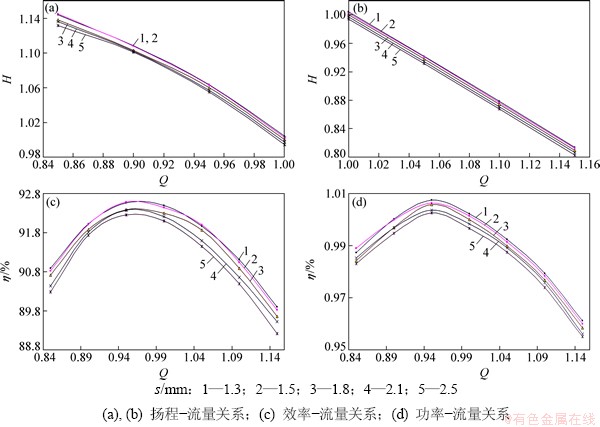
图7  不同叶顶间隙时的性能归一化对比

Fig. 7  Comparisons of performance at different tip clearances

3  CFD性能分析与校验

喷泵三元设计所得到混流式喷水推进泵后，运用CFD数值模拟的方法对其进行水力性能分析并检验设计结果是否达到选型所得的设计参数要求。

3.1  湍流模型、网格划分和边界条件设置

CFD方法是在流体控制方程下对喷泵内流动进行数值模拟。在定常条件下，应用不可压缩的三维连续方程和RANS方程模拟流体性能。本研究利用有限体积法对RANS偏微分方程进行离散，进而对其进行数值求解。采用SST剪切应力模型来封闭方程组，其集合了κ-ε模型和κ-ω模型的优点, 在近壁面区域，采用κ-ω模型模拟，湍流耗散较小，收敛性好。在湍流充分发展区域，采用κ-ε模型，计算效率高，对复杂流场的适应性更好^[16]。2种模型的结合能够较好地模拟黏性底层的流动。本文利用CAD软件UG构造该泵的几何模型，并采用全结构化网格进行网格划分，叶轮及导叶的网格如图8所示。计算得到壁面Y+小于150，满足SST湍流模型对壁面流动的模拟要求。

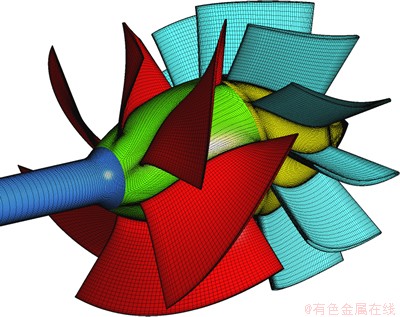
图8  网格划分

Fig. 8  Mesh of waterjet axial-flow pump

叶轮单通道网格数量18万，导叶单通道网格10万，喷口与进流直管网格100万，控制域全通道网格300万，由网格无关性计算曲线(图9)可知网格数达到300万时泵的水力性能曲线基本达到平衡，不再有较大波动，即满足流场模拟求解精度要求。计算域的大小及边界条件设置如图10所示。采用流量进口和压力出口，叶轮和轮毂设为相对静止壁面条件，泵壳设为绝对静止壁面条件。

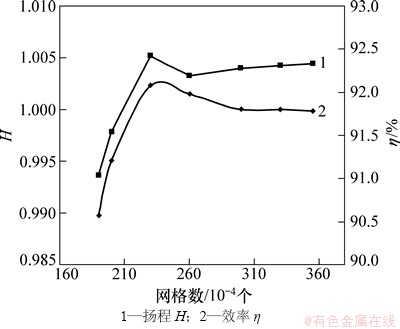
图9  网格数目无关性验证

Fig. 9  Validation of mesh number irrelevancy

图10  边界条件设置

Fig. 10  Boundary condition of numerical simulation

3.2  轴流泵水力性能分析与验证

对已完成设计的轴流式喷水推进泵在额定转速下、不同流量工况下的水力性能进行计算，计算结果如表1所示，水力性能曲线见图11。由图11可以看出：在设计工况下功率消耗允许范围内，扬程达到设计要求，效率达到92.3%。并在较大流量范围内喷泵效率都在89%以上，高效范围较宽，满足船舶航速变化对喷水推进泵的要求。本文计算得到气蚀余量理论值后，以总压形式在泵进口处加载进行数值模拟来验证其空化性能，结果如图12所示，图中非红色区域为空化区域。由图11可知：基本无大面积空化，仅在叶片导边处由于相对速度过快有微小空化，总体来说满足喷泵设计空化要求。

图13所示为该喷泵内部三维流线图，清楚显示了泵内流动情况，喷口出流均成轴向方向，这说明导叶整流效果好。

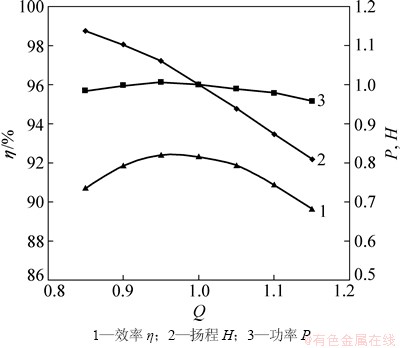
图11  扬程H、功率P和效率η特性曲线

Fig. 11  Characteristic curves of head, power and efficiency

图12  叶轮叶片表面空化验证

Fig. 12  Cavation performance of rotor blades

图13  喷泵内部三维速度流线图

Fig. 13  Three-dimension streamline in waterjet pump

4  结论

(1) 随喷口轴向长度增加，喷泵效率呈下降趋势，但喷泵产生推力和消耗轴功率存在1个最大值。该轴向长度下产生推力最大，对应轴功率最大，喷口整流效果最好。

(2) 叶轮叶片随边与导叶导边的轴向距离对泵的扬程、效率、消耗轴功率等水力性能指标有直接影响，泵内流体的流动情况也会随之变化。在距离增大的过程中泵的性能会出现起伏，存在最优值，此时叶轮叶片与导叶叶片的匹配效果最佳，流动损失最小，泵效率最高。经研究分析，认为最优轴向距离为轴流泵进口直径的3%~4%。

(3) 叶顶间隙越小，泵水力效率、扬程越高，轴功率越大。应该在制造和安装工艺许可的前提下，保证合适的叶顶间隙。

(4) 运用三元不考虑黏性的反问题与全三维考虑黏性的正问题迭代计算的方法对某轴流式喷水推进泵进行水力设计，设计过程高效、快捷、优质。对三元方法所设计的轴流式喷水推进泵采用CFD方法进行性能数值预报，结果满足设计指标，在较宽流量内具有高效率和良好的抗空化性能，这间接验证了三元设计方法的有效性和先进性。

参考文献：

[1] Bulten N. Numerical Analysis of a Waterjet propulsion system[D]. Eindhoven, the Netherlands: The Eindhoven University of Technology. Department of Mechanical Engineering, 2006: 5-9.

[2] 刘承江, 王永生, 丁江明, 等. 现代喷水推进装置的演变[J]. 舰船科学技术, 2006, 28(4): 8-12.

LIU Chengjiang, WANG Yongsheng, DING Jiangming, et al. The evolution of the modern waterjet marine propulsion unit[J]. Ship Science and Technology, 2006, 28(4): 8-12.

[3] Allison J L. Marine waterjet propulsion[J]. Transaction of SNAME, 1993, 101: 275-335.

[4] Allison J L, Jiang C B. Modern tools for waterjet pump design and recent advances in the field[C]//International Conference on Waterjet Propulsion Ⅱ. Amsterdam, Netherlands: RINA, 1998: 128-142.

[5] 汤方平. 喷水推进轴流泵设计及紊流数值分析[D]. 上海: 上海交通大学船舶海洋与建筑工程学院, 2006: 1-3.

TANG Fangping. Design and turbulence numerical analysis of waterjet axial-flow pump[D]. Shanghai: Shanghai Jiao Tong University, School of Naval Architecture. Ocean & Civil Engineering, 2006: 1-3.

[6] GAO Hong, LIN Wanlai, DU Zhaohui. Numerical flow and performance analysis of a water-jet axial flow pump[J]. Ocean Engineering, 2008, 35(16): 1604-1614.

[7] 靳栓宝, 王永生, 杨琼方. 基于数值试验的喷水推进轴流泵的一体化设计[J]. 中国造船, 2010, 1(3): 39-45.

JIN Shuanbao, WANG Yongsheng, YANG Qiongfang. Design on a waterjet axial-flow pump coupled with performance prediction by numerical simulation[J]. Shipbuilding of China, 2010, 1(3): 39-45.

[8] 彭国义. 轴流式水轮机转轮三维反问题计算与优化[D]. 北京: 清华大学机械工程系, 1996: 56-70.

PENG Guoyi. Three-dimensional rotational flow inverse computation and optimum design of Kaplan runner[D]. Beijing: Tsinghua University. Department of Mechanical Engineering, 1996: 56-70.

[9] 罗兴琦. 混流式水轮机转轮的全三维反问题计算与优化[D]. 北京: 清华大学机械工程系, 1995: 25-84.

LUO Xingqi. Full three-dimensional inverse and optimum design of francis runner[D]. Beijing: Tsinghua University. Department of Mechanical Engineering, 1995: 25-48.

[10] Zangeneh M. A compressible three dimensional blade design method for radial and mixed flow turbomachinery blades[J]. Journal of Numerical Methods in Fluids, 1991, 13: 599-624.

[11] Tan C S, Hawthrone W R, Mccune J E. Theory of blade design for large deflections: part2 annular cascades[J]. ASME Journal of Engineering for Gas Turbines and Power, 1984, 106(2): 354-365.

[12] 常书平, 王永生, 靳栓宝. 轴流式喷水推进泵水力设计和性能检验[J]. 哈尔滨工程大学学报, 2011, 32(10): 1278-1282.

CHAGN Shuping, WANG Yongsheng, JIN Shuanbao. Hydraulic design and performance investigation of a waterjet axial-flow pump[J]. Journal of Harbin Engineering University, 2011, 32(10): 1278-1282.

[13] Goto A, Nohmi M, Sakurai T, et al. Hydrodynamic Design System for Pumps Based on 3-D CAD, CFD, and Incerse Design Method[J]. Journal of Fluids Engineering, 2002, 124: 329-335.

[14] Bonaiuti D, ZANGENEH M, Aartojarvi R, et al. Parametric design of a waterjet pump by means of inverse design, CFD calculations and experimental analyses[J]. ASME Journal of Fluids Engineering, 2010, 132: 1-15.

[15] 关醒凡. 现代泵技术手册[M]. 北京: 宇航出版社, 1995: 14-21.

GUAN Xingfan. Modern pump techno-manual[M]. Beijing: Astronautic Press, 1995: 14-21.

[16] Lloyd G, Espanoles. A best practice guidelines for marine applications of computational fluid dynamics[R]. Washington: Atkins Consultants and Members of the NSC, Marnet-CFD Thernatic Network, 2002: 35-58.

(编辑  陈爱华)

收稿日期：2013-08-31；修回日期：2013-11-22

基金项目：国家自然科学基金青年基金资助项目(51309229)

通信作者：彭云龙(1989-)，男，河北邯郸人，博士研究生，从事喷水推进研究；电话：15871709967；E-mail：flydragonboys@163.com