DOI：10.19476/j.ysxb.1004.0609.2019.12.12

Ni-Mn-Ga合金磁热效应的组分调节与等静压调控

胡粉娥^{1, 2}，曹义明¹，魏生贤¹，陶  昌^{1, 3}，何禧佳¹，康艳茹¹，李  哲¹

(1. 曲靖师范学院 磁性材料及器件研究中心，曲靖 655011；

2. 曲靖师范学院 化学与环境科学学院，曲靖 655011；

3. 曲靖师范学院 物理与电子工程学院，曲靖 655011)

摘  要：Ni-Mn-Ga合金磁热效应的优化是制冷工程的研究热点之一。为深入研究Ni-Mn-Ga合金的磁热效应，以Ni_54+xMn_19-xGa₂₇ (x=0、0.4、1.0，摩尔分数)为研究对象，利用实验手段研究了合金的相变特性、组分及等静压对合金磁热效应的优化与调控作用。结果表明：随着Ni含量的增加，Ni_54+xMn_19–xGa₂₇合金的马氏体相变温度逐渐升高，而居里温度则先减小再增大；当x=1.0时，合金出现了磁-结构相变。相同外加磁场时，合金的最大磁熵变的绝对值(|ΔS_M|_max)及制冷量(W_RC)随Ni含量的增加而增大。当磁场改变3 T时，合金x=1.0对应的|ΔS_M|_max和W_RC最大、约为8.2 J/(kg·K)和53.61 J/kg，分别是x为0、0.4的3.04、2.28倍与3.31、1.67倍。0.58 GPa等静压对合金x=1.0的|ΔS_M|_max影响可忽略不计，但等静压的应用有利于拓宽合金的相变温区、致使合金W_RC提高了43.82%。为便于比较和工程应用，给出了合金|ΔS_M|_max、W_RC与外加磁场H的依赖关系。研究结果为Ni-Mn-Ga合金磁热效应的优化、调控及工程应用具有较好的指导意义。

关键词：Ni-Mn-Ga合金；磁制冷；马氏体相变；磁热效应；等静压

文章编号：1004-0609(2019)-12-2793-09　　     中图分类号：O469　　     文献标志码：A

与气体压缩式制冷技术相比，固态磁制冷技术因其具有结构紧凑、低噪声、高效率(效率可达卡诺循环的30%~60%，压缩式制冷效率只有卡诺循环的5%~10%)^[1]、节能(比压缩式制冷节能20%~30%^[2])、绿色环保^[3-5]等优点而备受关注。因此，固态磁制冷技术常常被公认为气体压缩式制冷技术的替代技术^[6-8]。此技术采用固态材料作为制冷剂，其典型代表有Gd-Si-Ge^[9-10]、La-Fe-Si(-H)^[11-13]、Mn-Fe-P-As^[14]、Ni-Mn-Ga^[15-16]、Mn-As-Sb^[17-18]等化合物，它们发生磁-结构相变(即一级马氏体相变与二级居里转变同时发生的相变)时具有较大的磁热效应。但Gd-Si-Ge、La-Fe-Si(-H)化合物中含有稀土元素，价格昂贵；Mn-Fe-P-As、Mn-As-Sb中含有剧毒元素(As)；而Ni-Mn-Ga合金的组成元素无毒、生物相容性强、成本相对低廉^[19-20]，合金制备简单、易实现大规模生产与推广应用，是近年来磁制冷材料的重点研究对象之一。

研究表明，Ni₂MnGa合金在降温过程中会发生2个分离的相变^[21-22]：在居里温度(T_C≈376 K)点附近发生顺磁到铁磁的二级相变(也称为居里转变)；随着温度的进一步降低，合金在202 K(此温度为马氏体相变温度，记为T_M)附近发生铁磁奥氏体到铁磁马氏体的一级热弹性马氏体相变。进一步研究显示，T_M与T_C对合金组分较为敏感。在Ni_2+xMn_1-xGa合金中，利用Ni部分替代Mn可使T_M逐渐增大、T_C逐渐减小^[23-24]。当T_M=T_C时，Ni-Mn-Ga合金的上述2个相变合为1个相变，即形成磁-结构相变^{[15, 25-28]}。发生磁-结构相变时，合金会展现出显著的磁热效应^{[15, 23, 25-28]}，这为磁热效应的优化和调控提供了有效途径。另外，等静压(p)的应用对Ni-Mn-Ga合金的磁热效应影响较大^[28-31]。ALBERTINI等^[30]的研究显示，等静压对富Ni与富Mn合金的磁热效应存在相反的影响：随着等静压的增大，富Ni合金的最大磁熵变的绝对值|ΔS_M|_max逐渐减小；而富Mn合金的|ΔS_M|_max则得到了显著提升。随后，MANDAL等^[31]在0.8 GPa作用下测试了富Ni合金的磁热效应，结果表明，等静压作用下|ΔS_M|_max略有减小。DEVARAJAN等^[28]对Ni_2–xMn_1+xGa合金的磁热效应进行了详细研究，结果发现，对于x=0的合金，加压过程中|ΔS_M|_max由19.2 J/(kg·K) (p=0 GPa) 降至6.04 J/(kg·K) (p= 0.969 GPa)；而对于x=0.15的合金，|ΔS_M|_max由8.9 J/(kg·K) (p=0 GPa) 减小至 1.27 J/(kg·K) (p=0.74 GPa)。即随着等静压的增大，上述两种合金的|ΔS_M|_max急剧下降。上述有限的研究结果显示，等静压对Ni-Mn-Ga合金磁热效应存在不一致的影响。此方面的研究相对不足，有待于进一步研究。

为了优化Ni-Mn-Ga合金的磁热效应，本文利用组分调节和等静压调控对该体系合金的磁熵变及制冷量进行了实验研究。结果显示，对于Ni_54+xMn_19–xGa₂₇ (x=0、0.4、1.0)合金，随着Ni含量的增加，T_M与T_C逐渐靠近、|ΔS_M|_max与制冷量随外加磁场(H)逐渐增大。对于x=1.0的合金，T_M=T_C，当H达3 T时，合金的|ΔS_M|_max和制冷量分别为8.20 J/(kg·K)和53.61 J/kg。等静压对|ΔS_M|_max(x=1.0)的影响可忽略不计，但对制冷量具有较好的激励作用。当p=0.58 GPa、H=3 T时，合金x=1.0的|ΔS_M|_max与制冷量分别为7.93 J/(kg·K)和77.10 J/kg；等静压作用下，合金的制冷量增加了43.82%。研究结果对Ni-Mn-Ga合金磁热效应的优化、调控及工程应用具有较好的指导意义。

1  实验

实验选用纯度分别为99.98%、99.98%、99.999%的金属单质镍(Ni)、锰(Mn)、镓(Ga)为原料，采用WK2型非自耗高真空电弧炉，在高纯氩气保护下制备名义组分为Ni_54+xMn_19–xGa₂₇ (x=0、0.4、1.0)的多晶样品。为使样品成分均匀, 所有样品均在磁搅拌作用下反复熔炼4次。将熔炼后的样品密封在氩气保护的真空石英管中，1 073 K高温环境中退火72 h，然后快速投入冰水混合物中进行淬火处理。利用SYJ-150型低速金刚石切割机进行样品切割，选取样品的中间部分用于测试合金的真实组分、相变特性以及磁热效应。样品的真实组分由附带能量色散光谱仪(Energy-dispersive spectrometer，EDS)的扫描电子显微镜(Scanning electron microscope，SEM)进行确定。样品的相变温度由TA Instruments DSC 2000型差示扫描热分析仪(Differential scanning calorimetry，DSC)加以测定，测试速率为10 K/min。利用物性测量系统(美国Quantum Design 公司)的振动样品磁强计(Vibrating sample magnetometer，VSM)测量样品的磁性，升降温速率为1.5 K/min。利用低场(0.05 T)下的磁化强度(Magnetization，M)与温度(T)之间的关系曲线[M(T)]确定样品的相变温度、居里温度(T_C)以及磁性、结构的转变；利用等温磁化曲线M(H)和Maxwell关系式计算合金的磁熵变。利用VSM附带的铜-铍夹型压力包(Copper–beryllium clamp-type pressure cell)进行样品等静压作用下的磁性测量，以便确定等静压对磁热效应的影响。

2  结果与分析

2.1  合金的组分与相变特性

Ni_54+xMn_19–xGa₂₇(x=0、0.4、1.0)合金的平均组分如表1所示。表1的数据显示，合金名义组分和实际组分基本一致，相对误差小于1.0%。因此，为方便书写，在以下的分析中，采用合金的名义组分进行描述。

表1  Ni_54+xMn_19–xGa₂₇合金的组分与马氏体转变温度

Table 1  Composition and martensitic transformation temperatures of Ni_54+xMn_19–xGa₂₇ alloys

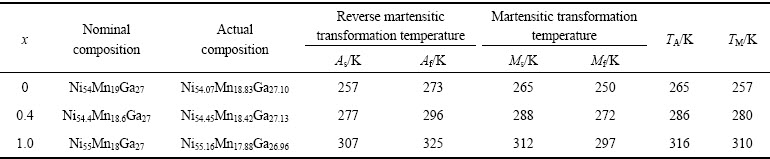
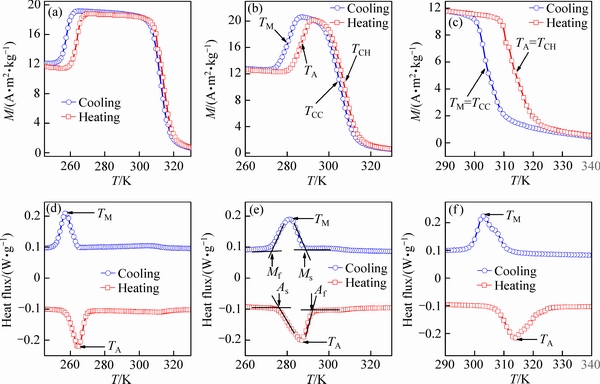
图1  Ni_54+xMn_19–xGa₂₇合金的低场磁化曲线与DSC曲线

Fig. 1  Low-field magnetization curves((a)-(c)) and DSC curves((d)-(f)) of Ni_54+xMn_19–xGa₂₇ alloys

图1所示为Ni_54+xMn_19–xGa₂₇合金的DSC曲线与低场(0.05 T)下的磁化曲线M(T)，其中图1(a)~(c)表示合金的M(T)曲线、图1(d)~(f)所示为合金的DSC曲线。图中，M_s、M_f、T_M和A_s、A_f、T_A分别表示正、反马氏体相变开始温度、结束温度及其峰值温度；T_CH与T_CC分别为加热和冷却时合金的居里温度。合金的相变温度由双切线法(如图1(e)所示)加以确定^[32]；峰值温度可由T_M=(M_s+M_f)/2，T_A=(A_s+A_f)/2加以估算。本实验所选合金样品的马氏体相变温度及相变峰温如表1所示。由图1和表1可知，合金相变温度及其峰值温度随x的增大而单调地增大。这一结果与前期关于Ni_50+xMn_25–xGa₂₅的报道高度一致^[33]。马氏体相变温度升高是由于Ni部分替代Mn致使合金晶胞体积减小、电子浓度增大而导致的^[34]。

图1(a)~(c)给出了合金在相变附近的M(T)曲线。图中曲线显示，对于x为0与0.4的合金，降温过程中发生了2个分离的相变，依次为二级居里转变与一级马氏体相变。随后的升温过程经历了一级反马氏体相变与二级居里转变。与x=0、0.4的合金不同，x=1.0的合金在升降温过程中只经历了1个相变，即出现了磁-结构相变。这就意味着，x=1.0的合金将展现出更大的磁热效应。此外，由加热和冷却的M(T)求导曲线dM/dT的极小值^[33]可知，合金的居里温度分别为：x=0时，T_CH=313 K、T_CC=312 K；x为0.4时，T_CH=307 K、T_CC=306 K；x=1.0时，T_CC=T_M=310 K，T_CH=T_A=316 K。

基于上述分析及表1数据可知，对于Ni_54+xMn_19–xGa₂₇合金，当x从0增至1.0时：1) 升温过程，T_A从265 K增至316 K，T_CH由 313 K降至307 K、再增至316 K；2) 降温过程，T_M由257 K增至310 K，T_CC由312 K降至306 K、再升至310 K。当x=1.0时，T_CC=T_M，T_CH=T_A，合金出现了磁-结构相变。

2.2  合金的磁热效应

合金磁热效应的大小由等温磁熵变(ΔS_M)及制冷量(Refrigeration capacity, W_RC)两个参数加以表征。相同外加磁场下，其数值越大则磁热效应越显著。

2.2.1  合金的等温磁熵变

等温磁熵变可由麦克斯韦关系式(Maxwell relation)的数值积分加以确定^{[26, 35-36]}

                   (1)

式中：M为磁化强度，A·m²/kg；H为磁场强度，T；T为温度，K；M(T, H)为等温磁化曲线，常简写为M(H)。

为了利用式(1)计算材料的等温磁熵变，首先必须测试材料的等温磁化曲线。Ni_54+xMn_19–xGa₂₇合金相变附近部分温度点的等温磁化曲线如图2(a)~(c)所示。测试时，合金x为0、0.4、1.0对应的测温范围分别为240~290 K、270~310 K、290~340 K，磁场范围0~3 T，每隔2 K测一条等温磁化曲线。为减小测试误差，每次测量前首先将样品在零磁场下加热到最高温度(如x=0的合金，最高温度设为290 K)，然后零场降温至测温点，再加磁场进行测试。为了较为清楚地显示各温度下合金磁化强度随外加磁场的变化情况，本文精选了相变附近部分温度点的磁化曲线绘于图2(a)~(c)。由图2(a)~(b)可知，在整个测试温区，x为0与0.4的合金均处于铁磁态。对于x=1.0的合金，温度高于320 K后合金处于顺磁态，温度低于304 K时合金处于铁磁态，而304~320 K区间合金展现出顺磁与铁磁共存状态。这些结果与图1(a)~(c)所示结果一致。

利用式(1)及合金的等温磁化曲线，本研究获得了Ni_54+xMn_19–xGa₂₇合金等温磁熵变，如图3(a)~(c)所示。由图3(a)~(c)可知，1) 随着磁场H的增大，合金磁熵变的负值(-ΔS_M)逐渐增大、在T_M附近出现极大值。2) 随着Ni含量的逐渐增大，相同磁场下-ΔS_M的峰值(即|ΔS_M|_max)逐渐增大。3) 当H改变3 T时，合金x为0、0.4、1.0对应的|ΔS_M|_max分别为2.7、3.6、8.2 J/(kg·K)。由于x=1.0的合金发生了磁-结构相变，其|ΔS_M|_max是最大的，分别是合金x为0、0.4的3.04倍与2.28倍。

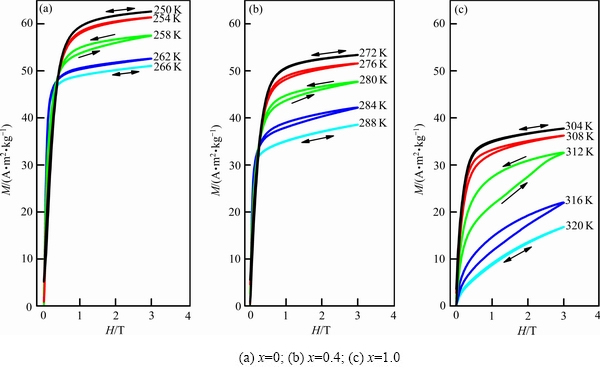
图2  Ni_54+xMn_19–xGa₂₇合金的等温磁化曲线

Fig. 2  Isothermal magnetization curves of Ni_54+xMn_19–xGa₂₇ alloys (arrows indicating directions of increasing and decreasing magnetic field)

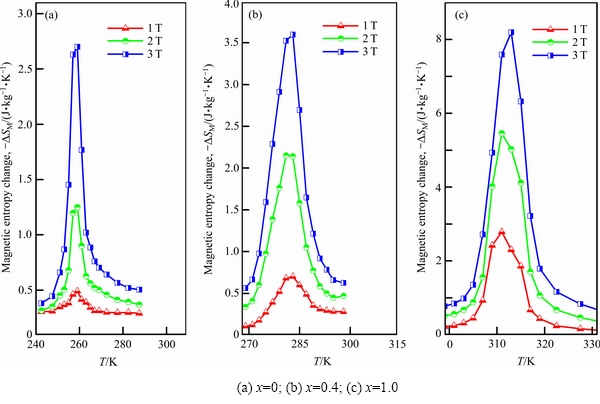
图3  Ni_54+xMn_19–xGa₂₇合金的等温磁熵变

Fig. 3  Isothermal magnetic entropy changes of Ni_54+xMn_19–xGa₂₇ alloys

进一步观察发现，外加磁场H变为3 T时，合金的|ΔS_M|_max并未达到饱和，即|ΔS_M|_max随H的增加而增加，如图4(a)所示。通过线性拟合，该研究获得了合金|ΔS_M|_max与外加磁场H的关系：

x=0时，

|ΔS_M|_max=-0.2171+0.9029 H，R²=0.95             (2)

x=0.4时，

|ΔS_M|_max=-0.2682+1.2434 H，R²=0.98             (3)

x=1.0时，

|ΔS_M|_max=-0.0404+2.7393 H，R²=0.99             (4)

式中：R²为线性拟合的相关系数。利用式(2)~(4)可快速地估算Ni_54+xMn_19–xGa₂₇合金在不同外加磁场下的最大磁熵变。

2.2.2  合金的制冷量

合金的制冷量可由(-ΔS_M)-T曲线(见图3(a)~(c))半高宽的积分加以估算，即^[36-37]

                       (5)

式中：T₁、T₂分别为(-ΔS_M)~T曲线半高宽的起、止温度，K。不同磁场下，合金的制冷量如图4(b)所示。结果显示：1) 随着磁场H的增加，合金制冷量W_RC线性增加。2) 当H=3 T时，合金x为0、0.4、1.0时对应的制冷量分别为16.2、32.01、53.61 J/kg。合金x=1.0的制冷量分别是x为0、0.4时的3.31、1.67倍，其缘由可归于合金x=1.0的磁-结构相变。3) 线性拟合结果如下

x=0时，

W_RC=-0.2568+5.1721 H，R²=0.98                (6)

x=0.4时，

W_RC =-2.0664+11.0186 H，R²=0.99               (7)

x=1.0时，

W_RC =0.2646+18.0036 H，R²=0.99                (8)

式(6)~(8)为Ni_54+xMn_19–xGa₂₇合金在不同外加磁场下的制冷量的估算提供了方便。

综上分析可知，由于x=1.0的合金发生了磁-结构相变，磁场改变3 T时，其|ΔS_M|_max与W_RC是最大的、分别为合金x为0、0.4的3.04、2.28与3.31、1.67倍。

2.3  压力对磁热效应的影响

由于x=1.0的合金具有较大的磁热效应，下面以此合金为研究对象，研究等静压对其磁热效应的影响。切取10 mg左右的样品，将其放入铜-铍夹型压力包中，加压至0.42 GPa与0.58 GPa，利用物性测量系统测试样品的等温磁化曲线，以便计算等静压下的等温磁熵变，其结果如图5(a)所示。图中数据显示：1) 相同外加磁场下-ΔS_M的峰值随等静压的增加而略有减小，这与文献[30-31]的结果基本一致，但减小幅度较小。例如，磁场变化3 T时，0、0.42、0.58 GPa对应-ΔS_M的峰值分别为8.2、8.01、7.93 J/(kg·K)；与0 GPa的数值相比，0.58 GPa对应-ΔS_M的峰值仅减小了0.27 J/(kg·K)，即减小幅度可忽略不计。等静压作用下合金的磁熵变保持不变，这对合金的工程应用是非常有利的。2) 等静压的作用致使相变温区大幅度拓宽，有利于(-ΔS_M)~T曲线半高宽的拓宽和合金制冷量的提高。

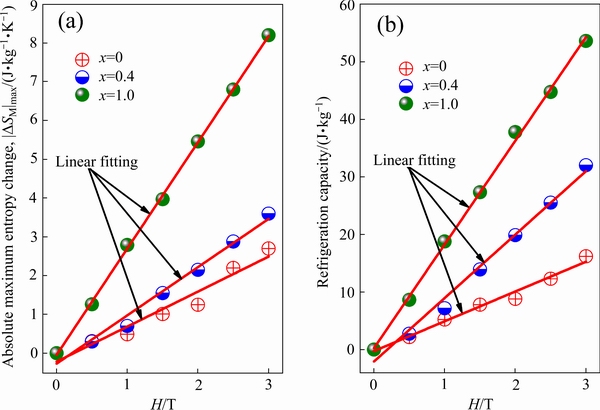
图4  Ni_54+xMn_19–xGa₂₇合金最大磁熵变的绝对值、制冷量与磁场的关系

Fig. 4  Relationships between absolute maximum entropy change, refrigeration capacity and magnetic field of Ni_54+xMn_19–xGa₂₇ alloys

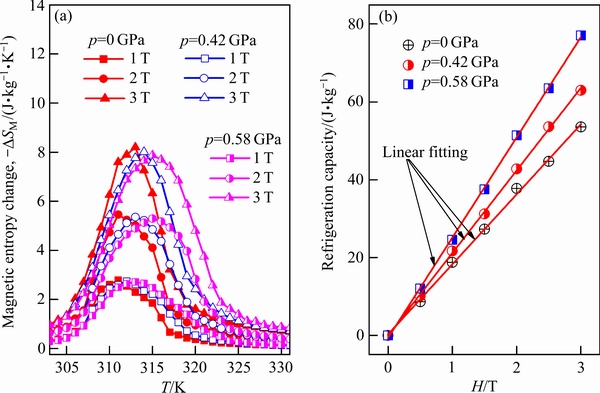
图5  Ni₅₅Mn₁₈Ga₂₇合金不同等静压下的等温磁熵变、制冷量与磁场的关系

Fig. 5  Relationships between isothermal magnetic entropy changes, refrigeration capacity and magnetic field of Ni₅₅Mn₁₈Ga₂₇ alloy under various hydrostatic pressures (0 GPa denotes one atmosphere)

图5(b)所示为不同压力下的制冷量与磁场H的依赖关系。结果显示：1) 等静压作用下的制冷量值与0 GPa数值的分离程度随磁场H的增加而逐渐增大。当H=3 T时，0.42、0.58 GPa对应的制冷量分别达到了63.01、77.10 J/kg。与0 GPa相比，制冷量分别增加了17.53%与43.82%，这是等静压作用下相变温区得到有效拓宽的缘故。2) 0.42、0.58 GPa作用下制冷量W_RC与H的依赖关系分别为

W_RC=-0.0511+21.2293 H，R²=0.99               (9)

W_RC=-0.6668+25.7921 H，R²=0.99              (10)

与式(8)的斜率相比，0.58 GPa压力下W_RC对H的敏感度提高了7.789 J/(kg·T)。

综上所述可知，0.58 GPa的等静压对Ni₅₅Mn₁₈Ga₂₇合金的最大磁熵变影响较小，可忽略不计。但由于等静压有效拓宽了合金的相变温区，大幅度提升了合金的制冷量。因此，等静压的应用可对合金磁热效应起到有效调控作用。

3  结论

1) 随着Ni含量的增加，合金Ni_54+xMn_19–xGa₂₇马氏体相变温度及相变峰温逐渐升高；居里转变温度则先减小再增大。当x=1.0时，合金正、反马氏体相变峰温T_M与T_A分别与降温、升温的居里温度相等，合金出现磁-结构相变。

2) 相同外加磁场下，合金Ni_54+xMn_19–xGa₂₇的最大磁熵变的绝对值|ΔS_M|_max与制冷量W_RC随Ni含量的增加而增加。当外加磁场H改变3 T时，合金x为0、0.4、1.0对应的|ΔS_M|_max与制冷量分别为2.7、3.6、8.2 J/(kg·K)与16.2、32.01、53.61 J/kg。

3) 对于x=1.0的合金，0.58 GPa等静压对其最大熵变|ΔS_M|_max影响较小，可忽略不计。但由于等静压的应用有效拓宽了合金的相变温区，致使合金的制冷量W_RC提高了43.82%。

4) 为便于比较和工程应用，文中给出了合金|ΔS_M|_max、W_RC与H的线性关系。对于x=1.0的合金，等静压的应用可显著提高制冷量W_RC对外加磁场H的敏感度、有利于提高合金的磁热效应。

REFERENCES

[1] Yu B f, Liu M, Peter W E, Andrej K. A review of magnetic refrigerator and heat pump prototypes built before the year 2010[J]. International Journal of Refrigeration, 2010, 33 (6): 1029-1060.

[2] VelAzquez D, Estepa C, Palacios E, Burriel R. A comprehensive study of a versatile magnetic refrigeration demonstrator[J]. International Journal of Refrigeration, 2016, 63: 14-24.

[3] Brück E, Tegus O, Cam Thanh D T, Trung N T, Buschow K H J. A review on Mn based materials for magnetic refrigeration: Structure and properties[J]. International Journal of Refrigeration, 2008, 31(5): 763-770.

[4] 高 湉, 齐宁宁, 孙 超, 吴 梅, 刘永生, 徐 燕, 周 桃. MnCo_0.95Cu_0.05Ge 合金的磁性及其磁热效应[J]. 中国有色金属学报, 2018, 28(8): 1597-1602.

GAO Tian, QI Ning-ning, SUN Chao, WU Mei, LIU Yong-sheng, XU Yan, ZHOU Tao. Magnetic properties and magnetocaloric effects in MnCo_0.95Cu_0.05Ge alloy[J]. The Chinese Journal of Nonferrous Metals, 2018, 28(8): 1597-1602.

[5] 亓淑艳, 马成国, 董丽敏, 韩志东, 张显友. Na⁺掺杂对钙钛矿La_0.7Sr_0.3-xNa_xMnO₃ 的结构及磁熵变的影响[J]. 中国有色金属学报, 2009, 19(5): 894-899.

QI Shu-yan, MA Cheng-guo, DONG Li-min, HAN Zhi-dong, ZHANG Xian-you. Effect of Na doping on structure and magnetic entropy of perovskite La_0.7Sr_0.3-xNa_xMnO₃ doped with Na⁺[J]. The Chinese Journal of Nonferrous Metals, 2009, 19(5): 894-899.

[6] 李振兴, 李 珂, 沈 俊, 戴 巍, 高新强, 郭小惠, 公茂琼. 室温磁制冷技术的研究进展[J]. 物理学报, 2017, 66(11): 110701.

Li Zhen-xing, Li Ke, SHEN Jun, Dai Wei, Gao Xin-qiang, Guo Xiao-hui, Gong Mao-qiong. Progress of room temperature magnetic refrigeration technology[J]. Acta Physica Sinica, 2017, 66(11): 110701.

[7] 郑新奇, 沈 俊, 胡凤霞, 孙继荣, 沈保根. 磁热效应材料的研究进展[J]. 物理学报, 2016, 65(21): 217502.

Zheng Xin-qi, Shen Jun, Hu Feng-xia, Sun Ji-rong, Shen Bao-gen. Research progress in magnetocaloric effect materials[J]. Acta Physica Sinica, 2016, 65(21): 217502.

[8] Romero G J, Ferreiro G R, Carbia C J, Romero G M. A review of room temperature linear reciprocating magnetic refrigerators[J]. Renewable and Sustainable Energy Reviews, 2013, 21: 1-12.

[9] James D M,Morrison K,Perkins G K,Deborah L S,Lograsso T A, Gschneidner K A, Pecharsky V K,Cohen L F. Metamagnetism seeded by nanostructural features of single-crystalline Gd₅Si₂Ge₂[J]. Advanced Materials, 2009, 21(37): 3780-3783.

[10] Pecharsky V K, Jr Gschneidner K A. Giant magnetocaloric effect in Gd₅(Si₂Ge₂)[J]. Physical Review Letters, 1997, 78(23): 4494-4497.

[11] FUJITA A, FUJIEDA S, HASEGAWA Y, FUKAMICHI K. Itinerant-electron metamagnetic transition and large magnetocaloric effects in La(Fe_xSi_1-x)₁₃ compounds and their hydrides[J]. Physical Review B, 2003, 67(10): 104416. 1-12.

[12] CHEN X, CHEN Y G, TANG Y B, XIAO D Q. Effects of solidification rate and excessive Fe on phase formation and magnetoclaoric properties of LaFe_11.6xSi_1.4[J]. Transations of Nonferrous Metals Society of China, 2017, 27(9): 2015-2021.

[13] Lyubina J, Nenkov K, Schultz L, Gutfleisch O. Multiple metamagnetic transitions in the magnetic refrigerant La(Fe, Si)₁₃H_x[J]. Physical Review Letters, 2008, 101(17): 177203.

[14] Tegus O, Brück E, Buschow K H J, de Boer F R. Transition-metal-based magnetic refrigerants for room- temperature applications[J]. Nature, 2002, 415 (6868): 150-152.

[15] Li Z B, Zhang Y D, SAnchez-ValdEs C F, SAnchez L J L, Esling C, Zhao X, Zuo L. Giant magnetocaloric effect in melt-spun Ni-Mn-Ga ribbons with magneto- multistructural transformation[J]. Applied Physics Letters, 2014, 104(4): 044101.

[16] Li Z, Xu K, Zhang Y L, Tao C, Zheng D, Jing C. Two successive magneto-structural transformations and their relation to enhanced magnetocaloric effect for Ni_55.8Mn_18.1Ga_26.1 Heusler alloy[J]. Scientific Reports, 2015, 5: 15143.

[17] Wada H, Tanabe Y. Giant magnetocaloric effect of MnAs_1-xSb_x[J]. Applied Physics Letters, 2001, 79(20): 3302-3304.

[18] Wada H, Morikawa T, Taniguchi K, Shibata T, Yamada Y, Akishige Y. Giant magnetocaloric effect of MnAs_1-xSb_x in the vicinity of first-order magnetic transition[J]. Physica B, 2003, 328(1/2): 114-116.

[19] Babita I, Gopalan R, Manivel R M, Chandrasekaran V, Ram S. Magnetostructural transformation, microstructure, and magnetocaloric effect in Ni-Mn-Ga Heusler alloys[J]. Journal of Applied Physics, 2007, 102(1): 013906.

[20] Duan J F, Long Y, Bao B, Zhang H, Ye R C, Chang Y Q, Wan F R, Wu G H. Experimental and theoretical investigations of the magnetocaloric effect of Ni_2.15Mn_0.85-xCu_xGa (x=0.05, 0.07) alloys[J]. Journal of Applied Physics, 2008, 103(6): 063911.

[21] Webster P J, Ziebeck K R A, Town S L, Peak M S. Magnetic order and phase transformation in Ni₂MnGa[J]. Philosophical Magazine Part B, 1984, 49(3): 295-310.

[22] Kreissl M, Kanomata T, Matsumoto M, Neumann K U, Ouladdiaf B, Stephens T, Ziebeck K R A. The influence of atomic order and residual strain on the magnetic and structural properties of Ni₂MnGa[J]. Journal of Magnetism and Magnetic Materials, 2004, 272/276(part 3): 2033-2034.

[23] Khovaylo V V, Buchelnikov V D, Kainuma R, Koledov V V, Ohtsuka M, Shavrov V G, Takagi T, Taskaev S V, Vasiliev A N. Phase transitions in Ni_2+xMn_1-xGa with a high Ni excess[J]. Physical Review B, 2005, 72: 224408.

[24] Albertini F, Pareti L, Paoluzi A, Morellon L, Algarabel P A, Ibarra M R, Righi L. Composition and temperature dependence of the magnetocrystalline anisotropy in Ni_2+xMn_1+yGa_1+z (x+y+z=0) Heusler alloys[J]. Applied Physics Letters, 2002, 81(21): 4032-4034.

[25] Cherechukin A A, Takagi T, Matsumoto M, Buchel’nikov V D. Magnetocaloric effect in Ni_2+xMn_1-xGa Heusler alloys[J]. Physics Letters A, 2004, 326(1/2): 146-151.

[26] Zhou X Z, Li W, Kunkel H. P, Williams G. Influence of the nature of the magnetic phase transition on the associated magnetocaloric effect in the Ni-Mn-Ga system[J]. Journal of Magnetism and Magnetic Materials, 2005, 293(3): 854-862.

[27] Hu F X, Shen B G, Sun J R, Wu G H. Large magnetic entropy change in a Heusler alloy Ni_52.6Mn_23.1Ga_24.3 single crystal[J]. Physical Review B, 2001, 64(13): 132412.

[28] Devarajan U, Esakki M S, Arumugam S, Singh S, Barman S R. Investigation of the influence of hydrostatic pressure on the magnetic and magnetocaloric properties of Ni_2–xMn_1+xGa (x=0, 0.15) Heusler alloys[J]. Journal of Applied Physics, 2013, 114(5): 053906.

[29] KamarAd J, Albertini F, Arnold Z, Casoli L, Pareti L, Paoluzi A. Effect of hydrostatic pressure on magnetization of Ni_2+xMn_1-xGa alloys[J]. Journal of Magnetism and Magnetic Materials, 2005, 290/291(part 1): 669-672.

[30] Albertini F, KamaraAd J, Arnold Z, Pareti L, Villa E, righi L. Pressure effects on the magnetocaloric properties of Ni-rich and Mn-rich Ni₂MnGa alloys[J]. Journal of Magnetism and Magnetic Materials, 2007, 316(2): 364-367.

[31] Mandal K, Pal D, Scheerbaum N, Lyubina J, Gutfleisch O. Effect of pressure on the magnetocaloric properties of nickel-rich Ni-Mn-Ga Heusler alloys[J]. Journal of Applied Physics, 2009, 105(7): 073509.

[32] Dong G F, Gao Z Y. Effect of heat treatment on the crystal structure, martensitic transformation and magnetic properties of Mn₅₃Ni₂₅Ga₂₂ ferromagnetic shape memory alloy[J]. Journal of Magnetism and Magnetic Materials, 2016, 399: 185-191.

[33] Entel P, Buchelnikov V D, Khovailo V V, Zayak A T,Adeagbo W A,Gruner M E,Herper H C, Wassermann E F. Modelling the phase diagram of magnetic shape memory Heusler alloys[J]. Journal of Physics D, 2006, 39(5): 865-889.

[34] Jiang C B, Muhammad Y, Deng L F, Wu W, Xu H B. Composition dependence on the martensitic structures of the Mn-rich NiMnGa alloys[J]. Acta Materialia, 2004, 52(9): 2779-2785.

[35] Wu R R, Bao L F, Hu F X, Wang J, Zheng X Q, Liu Y, Sun J R, Shen B G. Effect of substitution of In for Co on magnetostructural coupling and magnetocaloric effect in MnCo_1-xIn_xGe compounds[J]. Journal of Applied Physics, 2014, 115(17): 17A911.

[36] Zhang X. X, Qian M. F, Zhang Z, Wei L S, Geng L, Sun J F. Magnetostructural coupling and magnetocaloric effect in Ni-Mn-Ga-Cu microwires[J]. Applied Physics Letters, 2016, 108(5): 052401.

[37] Tanjore V J, Laura B, Jeffrey E S. Near room-temperature magnetocaloric properties of Gd-Ga alloys[J]. Journal of Magnetism and Magnetic Materials, 2014, 363: 201-209.

Composition adjustment and hydrostatic pressure control of magnetocaloric effect in Ni-Mn-Ga alloys

HU Fen-e^{1, 2}, CAO Yi-ming¹, WEI Sheng-xian¹, TAO Chang^{1, 3}, HE Xi-jia¹, KANG Yan-ru¹, LI Zhe¹

(1. Center for Magnetic Materials and Devices, Qujing Normal University, Qujing 655011, China ;

2. College of Chemistry and Environmental Science, Qujing Normal University, Qujing 655011, China;

3. College of Physics and Electronic Engineering, Qujing Normal University, Qujing 655011, China)

Abstract: The optimization, regulation and control of magnetocaloric effect (MCE) in Ni-Mn-Ga alloys are one of the main research hotspots in refrigeration engineering. In order to optimize the MCE of Ni-Mn-Ga alloys, the phase transformation properties and the effects of composition and hydrostatic pressure on MCE in Ni_54+xMn_19–xGa₂₇ (x=0.0, 0.4, 1.0) were experimentally studied and discussed. The results from heat flow data and magnetic measurements show that the martensitic transformation (MT) temperatures gradually increase with increasing the Ni content. However, the Curie temperatures first decrease and then increase with increasing Ni content. Importantly, a first-order coupled magnetic-structural transformation (MST), i.e., a simultaneous occurrence of the first-order MT and of the second-order magnetic transition, is observed in Ni-Mn-Ga alloys with x=1.0. Besides, absolute value of the maximum magnetic entropy changes (|ΔS_M|_max) and refrigeration capacity (W_RC) increases with the Ni content increase under the same magnetic field change. Furthermore, |ΔS_M|_max and W_RC are as large as 8.2 J/(kg·K) and 53.61 J/kg for the alloy with x=1.0 under a magnetic field change of 3 T. Such values in |ΔS_M|_max are approximately 3.04 and 2.28 times of those of alloys with x of 0 and 0.4, respectively. Meanwhile, the amplitude of W_RC for x=1.0 are about 3.31 and 1.67 times of those of alloys with x of 0 and 0.4, respectively. Much importantly, the hydrostatic pressure of 0.58 GPa has a marginal effect on |ΔS_M|_max in the alloy with x=1.0 while W_RC is enhanced by 43.82% resulting from the application of hydrostatic pressure to broaden the temperature window of phase transformation. For the sake of comparison and engineering application, the dependence of the external magnetic field on |ΔS_M|_max and W_RC is obtained by using the linear fitting method. These relationships can be used to rapidly estimate |ΔS_M|_max and W_RC in Ni_54+xMn_19–xGa₂₇ (x=0.0, 0.4, 1.0) alloys under various magnetic fields. The results are very meaningful for the optimization, adjustment and control and engineering application of magnetocaloric effect in Ni-Mn-Ga alloys.

Key words: Ni-Mn-Ga alloy; magnetic refrigeration; martensitic transformation; magnetocaloric effect; hydrostatic pressure

Foundation item: Projects(31760341, 51661029) supported by the National Natural Science Foundation of China; Project(2017FH001-054) supported by the Yunnan Local Colleges Applied Basic Research Projects of Yunnan Province, China; Project(201710684007) supported by the National Students’ Innovation and Entrepreneurship training program, Ministry of Education of China

Received date: 2018-12-07; Accepted date: 2019-03-11

Corresponding author: WEI Sheng-xian; Tel: +86-874-8987852; E-mail: wsx_8600@163.com

(编辑  李艳红)

基金项目：国家自然科学基金资助项目(31760341，51661029)；云南省地方本科高校联合专项-面上项目(2017FH001-054)；国家级大学生创新创业训练计划项目(201710684007)

收稿日期：2018-12-07；修订日期：2019-03-11

通信作者：魏生贤，教授，博士；电话：0874-8987852,；E-mail：wsx_8600@163.com