基于SVD的偏差补偿最小二乘估计算法
刘娜，张端金，杨林
(郑州大学 信息工程学院，河南 郑州，450001)
摘要：研究偏差补偿最小二乘估计问题。基于矩阵的奇异值分解(SVD)技术，提出一类偏差补偿最小二乘估计的递推算法(BCRLS)。通过对协方差进行奇异值分解，推导出自回归(AR)模型参数的估计算法。结果表明：与普通的偏差补偿算法相比，本算法提高了参数估计的稳定性和收敛速度。该算法更适用于带观测噪声的AR模型参数估计。
关键词：参数估计；AR模型；奇异值分解；偏差补偿最小二乘法
中图分类号：TP13 文献标志码：A 文章编号：1672-7207(2011)S1-0610-05
Bias compensated least squares estimation algorithm based on SVD
LIU Na, ZHANG Duan-jin, YANG Lin
(School of Information Engineering, Zhengzhou University, Zhengzhou 450001, China)
Abstract: The problem of bias compensated least squares estimation was studied. A new recursive estimation algorithm was presented based on the singular value decomposition (SVD). A parameter identification for auto-regression (AR) model was derived by SVD to covariance matrix. The results show that compared with the BCRLS algorithm, the proposed method improves the stability and convergence rate of parameter estimation. The algorithm is appropriate to AR model estimation with measurement noises.
Key words: parameter estimation; AR model; singular value decomposition; bias compensated recursive least squares
最小二乘法(RLS)是参数估计中最基本的方法。由于其算法简单、对系统要求不高、易于实现等优点被广泛应用于信号处理、控制、滤波、通信等领域。但是在这些领域中，常会遇到带观测噪声的AR模型参数估计问题。邓自立等[1]研究考虑AR模型的递推最小二乘辨识算法时发现，当其输入的噪声是白噪声时，可得到一致的参数估计；但输入噪声为有色噪声时，将会得到偏离的参数估计。同时还提出了带有色感测噪声AR模型参数估计的偏差补偿最小二乘法(BCLS)[2]。目前，矩阵分解广泛地用于控制和估计等领域，如U-D分解[3]、L-D分解[4]、SVD分解，其中基于SVD的研究受到了极大的关注[5-6]。奇异值分解是一种具有良好的数值稳定性、最好精度的分解方法，并且易于实现。张友民等[7]将SVD和RLS相结合，提出一种基于奇异值分解的递推最小二乘估计方法。基于此，本文作者将SVD技术应用于偏差补偿最小二乘估计，研究其收敛性和数值稳定性。
1 模型描述
考虑带有色观测噪声的平稳AR模型如下[1]：
(1)
(2)
(3)
式中：y(t)为真实信号；z(t)为观测信号；ω(t)是零均值、方差为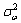
的白色观测噪声，且独立于零均值、方差为
的白噪声；αi是有待估计的系统参数。
定义参数向量和数据向量：
(4)
(5)
2 基本理论
2.1 奇异值分解SVD的基本原理
奇异值分解[7]首次由Beltrami和Jordon分别于1873年和1874年提出的。其核心是不改变信号矩阵的有关度量，得出矩阵的有效秩，得出在某种意义下矩阵降秩的最佳逼近。奇异值分解是线性代数中的一种重要的矩阵分解，广泛应用于信号处理、控制和统计学等领域。它是一种将矩阵对角化的正交变换，在某些方面与对称矩阵或Hermite矩阵基于特征向量的对角化类似，是矩阵分析中正规矩阵酉对角化的推广。
引理 若A为m×n阶实矩阵，设m ≤ n，则存在m阶正交阵U和n阶正交阵V，矩阵A的奇异值分解可表示为
(6)
式中： 
，
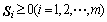为矩阵A的奇异值，且矩阵的前若干奇异值远大于其他的奇异值，
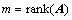(7)
，
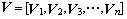是列正交矩阵,即满足
，
，矩阵U和V的列向量分别为左、右奇异向量。
若
是正定的，且A为对称正定阵，则A的奇异值可以简化成：
或 
(8)
即左、右奇异向量相等，在进行奇异值分解时，可减少计算量，仅需计算其中之一就行了。
由于奇异值分解具有稳定性、转置不变性、旋转不变性等特性，因此，基于奇异值分解的偏差补偿最小二乘算法具有较强的鲁棒性、稳定性及收敛性。
2.2 偏差补偿最小二乘法
由式(1)~(3)可得带有平稳有色观测噪声的AR(n)模型的偏差补偿最小二乘方法的一般表示形式如下：
(9)
(10)
(11)
(12)
其中：
,
,
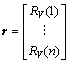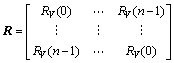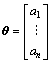
由式(3)可得有色观测噪声v(t)的相关函数
。
的方差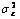
的估值算法：
(13)
(14)
(15)
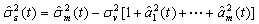(16)
算法的初值为
协方差矩阵P(t)在实际系统中，对舍入误差敏感，在传递的过程中使其失去对称正定性，从而影响该算法的数值稳定性。
3 SVD在偏差补偿中的应用
本文作者采用矩阵SVD来替换P(t)的计算更新，从而保证协方差的对称性和正定性，提高算法的精度和稳定性。按SVD分解原理存在如下的分解形式：
,
(17)
由式(9)和(11)可得：
(18)
由矩阵求逆引理，得
(19)
由式(16)对P(t)和P(t -1)进行奇异值分解，
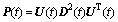(20)
(21)
将式(19)和(20)代入(18)，得
(22)
基于SVD的偏差补偿最小二乘法主要包括以下几个步骤：
步骤1 根据式(21)构造矩阵
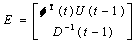(23)
由于P(t)是对称正定的矩阵，可知构造的矩阵E也是对称正定的，即也可进行SVD分解。
步骤2 对式(22)进行奇异值分解，其中
和
分别为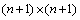
维和n×n维的矩阵，分别为矩阵E的左奇异阵和右奇异阵，
是一个
维对角
阵，其主对角线上的元素为E的奇异值，且为非负。
(24)
步骤3 利用式(25)和(26)更新U(t)和D(t)，得P(t)
(25)
(26)
步骤4 根据式(11)计算Q(t)。
步骤5 按照式(9)和(11)更新参数。
该算法最大的优点是通过对构造的矩阵E进行奇异值分解，得出奇异向量来更新U和D，即更新P(t)。
4 算法仿真
例：考虑带有色观测噪声的AR(2)模型
式中：和
是零均值、方差分别为
和
的独立高斯白噪声，已知
和
但
,
和
是未知的。
由
，得
分别应用SVD和BCRLS算法对上述的模型进行100次估计，再取均值，得出参数估计仿真结果，如图1和表1。
表1 参数估计结果(P(0)=10I)
Table 1 Estimation results of parameter (P(0)=10I)
图1 参数估计(P(0)=10I)
Fig.1 Estimation of parameter (P(0)=10I)
从图1可以看出，对于AR(n)模型，SVD算法和BCLS算法的跟踪曲线较为平稳，可得参数的无偏估计。与BCLS算法相比，SVD算法收敛速度较快，在仿真的初期能较早收敛于真实值，幅度小，稳定性能好，且易于并行实现。尽管SVD算法计算量稍大，但在一般应用问题中，系统的阶次不会太高，计算量增加较少。在本算法中，运行BCLS算法的时间tBCLS=0.013 3，运行SVD的时间tSVD=0.014 3。
协方差矩阵P(t)在实际系统中，对舍入误差敏感，容易失去对称正定性，从而影响递推算法的数值稳定性和收敛性，基于SVD方法可以缓解这一现象。通过仿真发现，初值P(0)的设置不同，会影响算法的精度和收敛速度，结果如图2所示。当P(0)增大时，BCLS算法收敛速度较慢，波动的幅度很大，对系统的要求较高；SVD算法收敛较快，能较好地收敛于真实值，跟踪曲线很稳定，对系统的要求较低。
图2 参数估计(P(0)=50I)
Fig.2 Estimation of parameters (P(0)=50I)
5 结论
(1) 在偏差补偿最小二乘估计算法的基础上，利用奇异值分解技术，提出AR(n)模型参数估计的递推算法。
(2) 该算法保留偏差补偿最小二乘算法的特性，给出系统参数的无偏估计，还提高了算法的精度、收敛速度和数值的稳定性。
参考文献：
[1] 邓自立, 王欣, 高媛. 建模与估计[M]. 北京: 科学出版社, 2007.
DENG Zi-li, WANG Xin, GAO Yuan. Modeling and estimation [M]. Beijing: Science Press, 2007.
[2] 邓自立. 自回归模型补偿偏差最小二乘辨识[J]. 黑龙江大学自然科学学报, 1981, 2: 10-20.
DENG Zi-li. Bias compensated least-squares identification for auto-regression model [J]. Journal of Natural Science of Heilongjiang University, 1981, 2: 10-20.
[3] Ljung L, Soderstom T. Theory and practice of recursive identification[M]. MIT Press, 1983.
[4] 向政, 富立, 范跃祖. L-D分解求逆法在联邦卡尔曼滤波中的应用[J]. 北京航空航天大学学报, 2003, 29(8): 749-752.
Xiang Zheng, Fu Li, Fan Yue-zu. Application of L-D factorization in calculating inverse in federated filter[J]. Journal of Beijing University of Aeronautics and Astronautics, 2003, 29(8): 749-752.
[5] Zhang You-min, Dai Guan-zhong, Zhang Hong-cai, et al. A SVD-based extended Kalman filter and application to aircraft flight state and parameter estimation [C]//Proceedings of 1994 American Control Conference, Maryland, 1994: 1809-1813.
[6] Aharon M, Elad M, Bruckstein A. K-SVD: An algorithm for designing over complete dictionaries for sparse representation [J]. IEEE Trans on Signal Process, 2006, 54(11): 4311-4322.
[7] 张友民, 李庆国, 戴冠中, 等. 基于奇异值分解的递推辨识方法[J]. 控制理论与应用, 1995, 12(2): 224-229.
ZHANG You-min, LI Qing-guo, DAI Guan-zhong, et al. A new recursive identification method based on singular value decomposition [J]. Control Theory and Applications, 1995, 12(2): 224-229.
[8] Goub G H, Van Loan C F. Matrix computations [M]. 2nd ed. London: The Johns Hopkings Press, 1989.
(编辑 龙怀中)
收稿日期：2011-04-15；修回日期：2011-06-15
基金项目：河南省教育厅自然科学基金资助项目(2010A510017)；郑州大学研究生教育支持基金资助项目(2009164)；郑州大学研究生科研基金资助项目(10L10502)
通信作者：张端金(1966-)，男，湖北荆州人，博士，教授，从事现代信号处理、故障检测与估计研究；电话：0371-67781545；E-mail: djzhang@zzu.edu.cn
