J. Cent. South Univ. Technol. (2011) 18: 2150-2156
DOI: 10.1007/s11771-011-0956-3
A new measuring method for maximal length, width and
thickness dimensions of coarse aggregates
DUAN Yue-hua(段跃华)1, 2, ZHANG Xiao-ning(张肖宁)1, WU Chuan-hai(吴传海)2
1. School of Civil Engineering and Transportation,South China University of Technology, Guangzhou 510640, China;
2. Guangdong Hualu Communications Technology Co., Ltd., Guangzhou 510420, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2011
Abstract: In order to establish a new method for measuring the dimensions of coarse aggregates, five different-size flat and elongated (F&E) coarse aggregates were glued into two specimens by epoxy resin, respectively, and slice images were obtained by X-ray CT, then the aggregates were extracted by the fuzzy c-means clustering algorithm. Attributions of the particle on different cross-sections were determined by the ‘overlap area method’. And unified three-dimensional Cartesian coordinate system was established based on continuous slice images. The coefficient values of spherical harmonics descriptor representing particles surface profile were gained, then each scanned particle was represented by 60×120 discrete points conformably with spherical harmonics descriptor. The chord length and direction angles were determined by the calculation. With the major axis (L) and orthogonal axis (W and T), the calculated results were compared with those measured by caliper. It is concluded that the new L, W, and T dimension measuring method is able to take the place of the present manual measurement.
Key words: coarse aggregate; flat and elongated (F&E) aggregate; X-ray CT; digital image processing; fuzzy c-means clustering; overlap area method; spherical harmonics
1 Introduction
Asphalt mixture is a kind of multiphase composite material among which the aggregates occupy a large proportion in volume and quantity. It is shown that the content of flat and elongated (F&E) coarse aggregates has significant influence on the performance of aggregates itself and asphalt mixture when they are used in asphalt mixture. QIN [1] has made a research on the effect of content of F&E limestone coarse aggregate upon the aggregates crushing value, skeleton formation as well as the high temperature stability and water stability of asphalt concrete. XIE et al [2] have conducted a research on the influence of F&E aggregates of different contents upon the voids, water stability, high temperature stability, fatigue resistance and damage percentage of AC-13C asphalt mixture. The F&E index of aggregates is of important research value, which cannot be ignored.
At present, it is stipulated by the National Industry Standard [3] that the content of F&E particles should be measured by vernier caliper. The measured particle is put on the table in stable situation, with its horizontal maximal length (hereinafter referred to as L), maximal thickness of its side (hereinafter referred to as T) and maximal width of particle (hereinafter referred to as W). Particles whose sizes conform to the equation L/T≥3 are F&E particles. It is stipulated in Japan and Europe that a particle can be defined as F&E particle when the ratio of its maximal length L and its thinnest breadth b is 3:1. Different experimental methods for different results of L/b (such as 2:1, 3:1 and 5:1) are listed in American ASTM D 4791-95, with special measuring equipments. Special caliper is used by EN 933-4 in Europe. However, at present, no caliper specifications are stipulated in explicit terms in China.
Traditional measurements of F&E particles are time-consuming, with low efficiency. Besides, the accuracy of measuring results cannot be guaranteed due to the manual operation.
Some scholars attempted to determine the indices of F&E particles by measuring the particle dimensions with digital image processing. For instance, MORA et al [4] developed a set device by mounting a camera on a photographic stand, the aggregate particles were properly poisoned in the sample tray, and the length and breadth of a particle were defined as the length and breadth of the bounding rectangle that would enclose the particle area in the image. MAERZ [5] determined the particle dimensions by transporting the particles with conveyer belt and capturing the right-above and lateral images of particles with two digital cameras, then the length and width were measured according to the plan view and the height was measured in the profile view. FERNLUND [6] photographed the particles in two positions, lying and standing, thus all three axes of each particle could be measured by the largest and smallest projected area using the images of the particles in these two positions. PAN et al [7] determined the length, width and thickness values by capturing the three-dimensional graphics of aggregate particles from three orthogonal angles with the help of UIAIA system and by comparing the dimensions of cross-section rectangles of three 2D particles.
From all the methods mentioned afore, it can be seen that the definitions of axes of aggregate particles vary greatly between different researchers and their image-analysis programs. Image analysis normally ground on two-dimensional images, and the Ferret diameters in the maximum projected area and the smallest projected area often used as dimensions with the two projected areas of a particle may not always be perpendicular. Obviously, the projected area of the aggregate particles photographed by the digital camera cannot reflect the true three-dimensional surface profile, so the dimensions determined by these digital image processing methods are not the real axes of the particles frequently.
Researchers developed different techniques for imaging particles in order to determine their 3D size and shape. For example, LEE et al [8] determined the three dimensional values of particles by indirectly capturing the three-dimensional surface information of particles, with triangulation of the upper part of aggregate under the help of laser facility. This approach overcame the shortcomings of the accuracy limitations of two-dimensional image analysis to a certain extent. However, the 3D data may be easily affected by laser speckle noise and color variations encountered in aggregates.
A new measuring method for the L, W, and T dimensions of coarse aggregates, compared to the traditional measurement, has been invented based on the digital image processing and image analysis.
In this work, continuous cross-sections of aggregate particles were obtained by X-ray CT which can accurately restore the complicated three-dimensional surface profile of particles and the L, W, and T dimensions and their direction angles were found and calculated based on a series of steps. This method can be even applied to detect the inner aggregate particles directly of asphalt mixture specimens in nondestructive way based on the special characteristics of X-ray CT.
2 Specimen preparations and scanning
This research is to determine the dimensions of flat and elongated (F&E) aggregates. Five elongated and five flat aggregate particles of different sizes are selected for the measurement of L, W, and T directions with the vernier caliper. The aggregate particles are glued by epoxy resin of good stickiness and stable physical and chemical property. Contact between particles is avoided for the spare of unnecessary trouble of digital image processing in later period caused by touched particles. The appearance of specimen is shown in Fig.1.

Fig.1 Scanning specimen of flat and elongated (F&E) aggregates
With the 225 kV industrial CT scanning equipment assembled by YXLON company, the planer resolution ratio of image is 1 024×1 024, interlayer spacing is one pixel, and both planer and axial pixel sizes are 0.108 mm. The imaging precision represents the high industrial technology level at present. The original cross-section scanning images are shown in Figs.2(a) and 2(d). Three-dimensional visualization can be realized by software, as shown in Figs.2(b) and 2(e).
3 Digital image processing for slice images
3.1 Segmentation of original cross-section images
Since the cross-sections are all pseudo-color images, three-dimensional information should be obtained by a series of digital image processing methods. For the specimen composed of coarse aggregate particles and epoxy resin, the density of these two materials is far different from each other. Theoretically, according to the imaging principle of industrial CT, the grey histogram of cross-section images is distributed in bimodal distribution. However, the factors of imaging inaccuracy are mainly the anisotropism of particles and the bubbles are produced in the solidification of epoxy resin. In consideration of the image characteristics, FCM (fuzzy c-means clustering method) are employed. Compared with the classic K-means which forcibly classifies a certain pixel into a category, FCM is clustering method based on division, with the introduction of membership grade in fuzzy mathematics, giving the possibilities of each pixel belonging to a certain category. The clustering objective function is
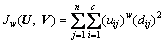 (1)
(1)
where U={uij} is the fuzzy membership grade matrix, representing that an object is a member of a set level function, V={vij} represents the cluster center set, dij=‖xj-vi‖ indicates the distance between the j-th pixels to the i-th cluster center, c represents the number of cluster categories (11, x2, …, xn}, for the n pixel sets to be clustered, the iterative optimization algorithm is adopted to minimize the calculation of the objective function Jw. As for the specific process, one can refer to Ref.[9].
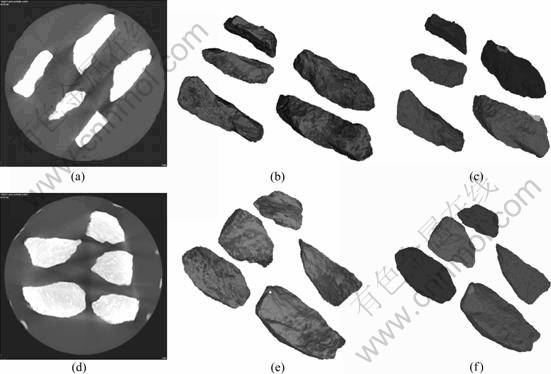
Fig.2 Original cross-section images and matching results: (a) Cross-section image of elongated particles; (b) Three-dimensional visualization of Fig.2(a); (c) Cross-sections matching result of Fig.2(a); (d) Cross-section image of flat particles; (e) three- dimensional visualization of Fig.2(d); (f) Cross-sections matching result of Fig.2(d)
Here, the internal material is divided into two categories and FCM is used in programming. Therefore, the aggregates can be extracted from the cross-section images for the next-step analysis.
3.2 Particle identification by cross-sections matching
Because CT scanning images are composed of a series of continuous cross-section images and the information of each aggregate particle is contained in different continuous cross-section sequences [10-12], proper matching method is employed to determine the attributes of each particle cross-section image, which will be beneficial to the three-dimensional analysis in the later period. This objective can be better achieved by ‘overlap area method’ and the equation is as follows:
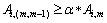 (m=2, 3, …, n) (2)
(m=2, 3, …, n) (2)
where m represents the number of layers of current section, n represents the total number of layers, α represents adjustable factor (0.6 is taken in this study), Ai,m represents the area of particle i in section m and Ai,(m,m-1) represents the overlap area of particle i in section m that is mapped to section m-1. This formula is based on the common sense that the variation of enlarged area of continuous particle cross-section will not happen, with repeating adjustment of coefficients and strict check on coarse aggregates of various sizes. The prerequisite for this formula is images of high resolution (HR), especially with minimal HR in the direction of Z-axis, which is able to guarantee the non-variation of particle cross-section area. The layer spacing of continuous cross-section sequences is one pixel, which fully satisfies the requirements of this formula.
With this formula matching, particle attributes can be determined accurately, as shown in Figs.2(c) and (f). Since the matching results are in full accord to the real results without omission of particle cross-section information, the attributes of any particle cross-section in the sequence map can be determined by this method.
4 Measuring method of L, W and T dimensions
4.1 Establishment of three-dimensional Cartesian coordinate system
The particle cross-section attributes can be recorded after determination. Related coordinate system and representation of aggregates surface profile under this system should be established in order to measure the three dimensions L, W and T.
Since all the CT scanning cross-section graphics are of the same size, two-dimensional Cartesian coordinate system for planer graph can be established. Suppose the coordinate in the lower left quarter of Figs.2(a) and 2(d) be (0, 0) and the coordinate of each pixel be consistent with the pixel position. For instance, for a picture of 1 024×1 024, the coordinate in the upper right corner is (1 024, 1 024). Similarly, the Z coordinate can be determined by the layers of cross-section sequences and graphic resolution. All resolution ratios of Z-axis of continuous cross-section sequences scanned at this time are of one pixel, consistent with the XY plane. In other words, the layer spacing is one pixel. Therefore, Z-axis coordinate of each cross-section image is in accordance with the present layers. For instance, for a particle in Fig.2(c), its continuous cross-section sequence is from 57 to 153 and the range of three-dimensional coordinate for the 100th layer is (0, 0, 100)-(1 024, 1 024, 100). Therefore, the three-dimensional Cartesian coordinate system for the pixels of each particle can be established.
Here, the three-dimensional coordinate figures with the pixel positions are not the real three-dimensional figures of particles. Figures of real physical length cannot be attained until the conversion of three-dimensional coordinate figures. The actual size of image pixel and measuring value can be obtained through the following formula, with the internal conversion coefficient ηip [13]:
 (3)
(3)
where dphy represents the actual distance in physical space, while dimg is the measured distance in image space.
At present, the industrial CT platform can automatically calculate the pixel values and give the feedback. Generally speaking, data obtained through this platform is true and reliable. It can also be tested by Eq.(3). The first step is to accurately measure the real length of a specimen which will later be scanned. Then, the internal conversion coefficient is calculated through the pixel spacing of the measured imaging.
4.2 Representation of three-dimensional contour of particles
In order to measure the dimensions of particles, first of all, information of all pixels constituting the three-dimensional contour of the particle surface should be obtained. For the CT scanning graphics of aggregate particles, the particle surface contour is composed of all the pixels belonging to its first cross-section image and its last cross-section image of its continuous cross-section sequences, and full perimeter pixels of this particle among all the cross-section graphics. An ordinary computer is not able to calculate the L, W and T dimensions of each particle pixel, so simplified method should be employed to describe the contour of particle cross-section. And the spherical harmonics descriptor is a good way for the shape matching of three-dimensional objects. The basic principle is as follows [14-17].
Assume that the surface points of a three-dimensional object in Cartesian coordinate system can be shown in Eqs.(4)-(6):
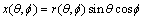 (4)
(4)
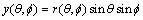 (5)
(5)
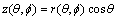 (6)
(6)
where r represents the distance from three-dimensional surface contour points to the centroid, θ represents the positive angle of directed line segment and Z axis, and f represents the angle that rotates counter clockwise from X-axis to directed line segment in the positive Z-axis view.
If r(θ, f) is smooth on unit sphere, and is assumed as cyclic distribution to θ, then it can be expressed as an extended form of spherical harmonic function, as shown in Eq.(7):
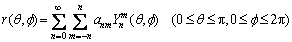 (7)
(7)
where anm is a coefficient.
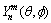 is referred to as spherical harmonic function, and its expression is as follows:
is referred to as spherical harmonic function, and its expression is as follows:
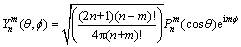 (8)
(8)
where 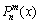 is referred to as associated Legendre function, which is a series of orthogonal polynomials. It should be pointed out that, in the case of m<0, the expression of
is referred to as associated Legendre function, which is a series of orthogonal polynomials. It should be pointed out that, in the case of m<0, the expression of 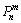 is shown in Eq.(9):
is shown in Eq.(9):
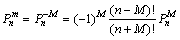 (9)
(9)
where m<0, and M>0.
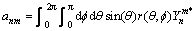 (10)
(10)
where anm is the coefficient, and 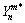 is the complex conjugate form of
is the complex conjugate form of 
After repeating the test and calculation, it is proper for the order n in Eq.(4) to be between 25 and 30. And for θ and f in Eq.(9), it is appropriate to use equal angle spacing in convenience of numerical integration. Theoretically, the smaller the original sampling interval, the more accurate the results. With the concept of equivalent diameter, suppose the particles to be standard spheres of the same superficial area. As the superficial area and cross-section image pixel size, each pixel is sampled theoretically. For instance, if both θ and f are calculated as 180, 1802=32 400 should be calculated in integration. The value of anm can be calculated through Eq.(7). When the order is n, the coefficient value is composed of (n+1)2 plural numbers. Compared with the method of recording all values of the aggregate particles, this representation of aggregate particles can substantially reduce the computer storage and numerical calculation.
4.3 Dimensional measurement and experimental verification of L, W, and T dimensions
The three-dimensional contour value r(θ, f) of any angle can be obtained by calculating the coefficient of each particle with the spherical harmonics descriptor. In other words, the contour of particles can be represented by a number of discrete points. Substitution of these values in Eqs.(4)-(6) can be conversed into the Cartesian coordinate system, which provides possibility to the calculation of L, W and T dimensions.
For the five flat and elongated (F&E) particles as shown in Fig.1, the three-dimensional Cartesian coordinate values with equal angle spacing are obtained by 60×120 discrete points. The distance between two discrete points (that is chord length) and their direction vector are calculated with its maximal chord L dimension. By comparing the included angles between the straight lines, all chords vertical to the L direction can be found out, among which the longest chord is W dimension. Then find out all chords both vertical to L and W directions, among which the longest chord is T dimension. For particles having a series of representation of discrete points, ±1.5° error is permitted in the comparison of included angles between straight lines so as to guarantee that there are enough backup chords for comparison.
All F&E particles are tested through this method, in which all parameters in the calculation keep the same. The final effect is shown in Fig.3. The calculated results and measured results of vernier caliper are listed in Table 1.
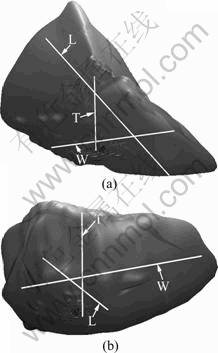
Fig.3 Measuring results of L, W and T dimensions: (a) Elongated particles; (b) Flat particles
From Table 1, we can conclude that the maximum relative error of the measurement of L, W and T dimensions is 9.3% and the minimum relative error is 0.6%. There is no obvious statistical dependency of relative error to flat and elongated attributes or compared dimensions of the particles.
The average value is 3.97% when all dimensional relative errors are analyzed, with standard deviation of 2.42 mm. These data prove that the calculation results of new measuring method are very close to the manual work results, but there still exists discrepancy.
However, the manually measured values are obtained by caliper according to the National Test Standard, so the data are not reliable because of being prone to errors through ignorance or negligence, and can only be regarded as reference. In addition, according to the test standards, the particle should be put on the table in stable situation and the maximal and minimal lengths of cross-section rectangle are measured in the plane position and lateral position. But sometimes, for the same particle, there are several different positions in which the particles can be put stably and it is hard to determine which one is the most appropriate. Even in a specified position, it is very hard to judge which cross-section of the aggregate should be measured because they resemble each other so much.
Table 1 Comparison between calculated and measured values
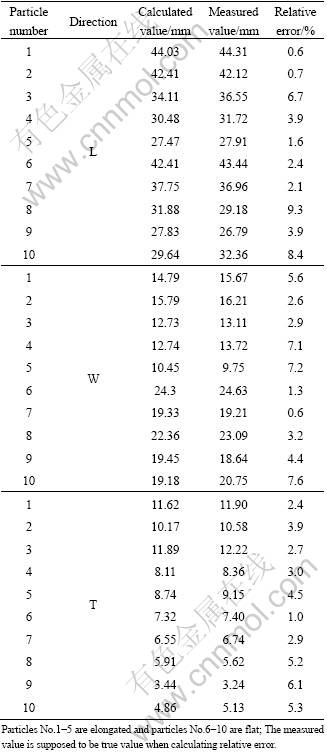
However, dimensions obtained through the numerical calculation procedures are the real maximal chords of three-dimensional surface contour of particles, and they are more accurate and unique for specify particle. All processes can be done by the computer automatically avoiding the artificial errors. Strictly speaking, these two methods have different physical meanings. Comparatively, the L dimension calculated by numeration can represent the long axis more accurately and the W and T dimensions obtained through this method are strictly orthotropic with L dimension in a given error range that cannot be guaranteed by the caliper measuring method. So, the manual measuring values are not the most accurate dimensions but can be used as reference.
Overall, the L, W and T dimensions calculated through this method are completely scientific and reliable in the control of flat and elongated (F&E) aggregate attributes, which can substitute the traditional measuring method.
5 Conclusions
1) A new measuring method for the L, W, and T dimensions of coarse aggregate is proposed for the identification of flat and elongated (F&E) attributes. With the industrial CT technology, the real three-dimensional information is fully retained whose advantages are much better than the particle images produced by digital camera or laser.
2) Digital image processing is used for the proper usage of three-dimensional information. The aggregate particles are extracted from and classified in different cross-section images and proper three-dimensional coordinate system is established.
3) The three-dimensional contour of particles can be represented by discrete points in spherical harmonics, which enables the calculation of L, W and T dimensions.
4) Through the new method, the long axis L and its orthogonal position with W and T can be accurately fixed, which is able to identify the content, incidence and position of flat and elongated (F&E) particle of concrete specimen. Compared with the traditional measuring method, many defects caused by manual measurement can be avoided and its measuring results are true and reliable, thus it can substitute the traditional method and other digital image measurements.
References
[1] QIN Lu-sheng. Study on quality criteria of flat and elongated particles and clay content in coarse aggregate for asphalt surface course [J]. Journal of Highway and Transportation Research and Development, 2009, 26(3): 17-21. (in Chinese)
[2] XIE Zhao-xing, LI Ding-le, HAN Sen, PENG Bo. Influence of percentage of flat and elongated particles on performance of asphalt mixture [J]. Journal of Building Materials, 2007, 10(6): 736-739. (in Chinese)
[3] JTG E42—2005. Test methods of aggregate for highway engineering [S]. Beijing: China Communications Press, 2005. (in Chinese)
[4] MORA C F, KWAN A K H, CHAN H C. Particle size distribution analysis of coarse aggregate using digital imaging processing [J]. Cement and Concrete Research, 1998, 28(6): 921-932.
[5] MAERZ N H. Technical and computational aspects of the measurement of aggregate shape by digital image analysis [J]. Journal of Computing in Civil Engineering, 2004, 18(1): 10-18.
[6] FERNLUND J M R. Image analysis method for determining 3-D shape of coarse aggregate [J]. Cement and Concrete Research, 2005, 35: 1629-1637.
[7] PAN T, TUTUMLUER E, CARPENTER S H. Effect of coarse aggregate morphology on permanent deformation behavior of hot mix asphalt [J]. Journal of Transportation Engineering, 2006, 132(7): 580-589.
[8] LEE J R J, SMITH M L, SMITH L N. A new approach to the three-dimensional quantification of angularity using image analysis of the size and form of coarse aggregates [J]. Engineering Geology, 2007, 91: 254-264.
[9] WANG Hai-bo, LI Xue-yao. Segmentation of intracranial hemorrhage CT image based on FCM clustering algorithm [J]. CT Theory and Applications, 2009, 18(2): 99-105. (in Chinese)
[10] Wang L B, FROST J D, LAI J S. Three-dimensional digital representation of granular material microstructure from X-ray tomography imaging [J]. Journal of Computing in Civil Engineering, 2004, 18(1): 28-35.
[11] FU Y R, WANG L B, TUMAY M T, LI Q B. Quantification and simulation of particle kinematics and local strains in granular materials using X-ray tomography imaging and discrete-element method [J]. Journal of Engineering Mechanics, 2008, 134(2): 143-154.
[12] WANG Y P, WANG L B, HARMAN T. Noninvasive measurement of 3D permanent strains in asphalt concrete using X-ray tomography imaging [C]// TRB, Annual Meeting CD-ROM, 2007.
[13] LU Yan-ping, WANG Jue, YU Hong-lin. 3D image processing and analyzing system for industrial computed tomography [J]. Chinese Journal of Scientific Instrument, 2009, 30(2): 444-448. (in Chinese)
[14] GARBOCZI E J. Three-dimensional mathematical analysis of particle shape using X-ray tomography and spherical harmonics: application to aggregates used in concrete [J]. Cem Concr Res, 2002, 32: 1621-1638.
[15] ERDOGAN S T, QUIROGA P N, FOWLER D W, SALEH H A, LIVINGSTON R A, GARBOCZI E J, KETCHAM P M, HAGEDORN J G, SATTERFIELD S G. Three dimensional shape analysis of coarse aggregates: Methodology and preliminary results on several different coarse aggregates [J]. Cement and Concrete Research, 2006, 36: 1619-1627.
[16] TAYLOR M A, GARBOCZI E J, ERDOGAN S T, FOWLER D W. Some properties of irregular 3-D particles [J]. Powder Technology, 2006, 162: 1-15.
[17] RYPL D. Using the spherical harmonic analysis and the advancing front technique for the discretization of 3D aggregate particles [J]. Advance in Engineering Software, 2010, 41: 38-45.
(Edited by YANG Bing)
Foundation item: Project(51038004) supported by the National Natural Science Foundation of China; Project(2009318000078) supported by the Western China Communications Construction and Technology Program, China
Received date: 2010-11-08; Accepted date: 2011-03-07
Corresponding author: ZHANG Xiao-ning, Professor, PhD; Tel: +86-20-87588879; E-mail: prozxn@163.com