DOI： 10.11817/j.issn.1672-7207.2020.08.003

长沙典型地层土压平衡盾构掘进参数及表现预测

杨果林¹,张沛然¹,陈亚军²,沈臻鑫²

（1. 中南大学 土木工程学院，湖南 长沙，410075；

2. 中建五局土木工程有限公司，湖南 长沙，410004）

摘要:为对长沙典型地层土压平衡盾构的掘进表现进行预测，基于实际工程采集的砾岩、砂卵石和泥岩地层盾构施工记录数据，对主要施工参数在3类地层中的分布及变化特征进行统计分析。研究贯入度、场切入指数和掘进比能三者间的变化关系，并讨论地层可掘性问题。根据贯入度、场切入指数和掘进比能分类提出考虑地层条件的净掘进速率预测方法及经验模型，并用于4类地层的盾构掘进表现预测分析。研究结果表明：贯入度的最小和最大平均值分别出现在泥岩和砂卵石地层中；刀盘扭矩在砂卵石和泥岩地层中变化幅度较大，而在泥岩地层中平均值最大；砂卵石地层的总推进力比其他2类地层的总推进力高30%左右，3类地层的总推进力对刀盘扭矩影响特征有所差异;贯入度、场切入指数和掘进比能三者间相关性较好，可作为表征地层可掘性的指标。所提出的净掘进速率预测模型对4类地层盾构掘进表现的预测效果较好，具有一定的适用性。

关键词:土压平衡盾构；掘进参数；表现预测；贯入度；场切入指数；比能；可掘性

中图分类号:U455.43                    文献标志码:A

文章编号:1672-7207（2020）08-2069-12

Excavation parameters and performance prediction of earth pressure balance shield in typical strata of Changsha

YANG　Guolin¹, ZHANG　Peiran¹, CHEN　Yajun², SHEN　Zhenxin²

(1. School of Civil Engineering, Central South University, Changsha 410075, China；

2. CCFEB Civil Engineering Co. Ltd., Changsha 410004, China)

Abstract: In order to predict the excavation performance of earth pressure balance shield in typical strata of Changsha, the earth pressure balance shield excavation recorded data of conglomerate, sandy gravel and mudstone strata were collected based on the actual project. The distribution and variation characteristics of the main excavation parameters in three types of strata were statistically analyzed. The relationship among penetration, field penetration index and specific energy of excavation was studied, and the problem of stratum boreability was discussed.According to the classification of penetration, field penetration index and specific energy, the prediction method and empirical model of net penetration rate considering stratum conditions were put forward and applied in the prediction of tunneling performance of earth pressure balance in four strata.The results show that the minimum and the maximum mean values of penetration appear in mudstone and sandy gravel strata respectively. The torques of cutter head vary greatly in sandy gravel and mudstone strata, and the mean value of mudstone strata is the largest. Total thrust of sandy gravel formation is about 30% higher than that of other two types of strata, and the influence of total thrust on the torque is different due to the difference of the geological conditions. The correlation among penetration, field penetration index and specific energy is good, which can be used as an indicator to express the stratum boreability. The prediction model of net penetration rate proposed in this paper has good prediction effect on the performance of earth pressure balance shield tunneling in four types of strata, and has certain applicability.

Key words: earth pressure balance shield; excavation parameters; performance prediction; penetration; field penetration index; specific energy; boreability

近年来，土压平衡(EPB)盾构在我国地下空间开发和建设中受到广泛重视和应用，同时也出现了大量相关研究和应用技术问题亟待解决。由于EPB盾构施工参数及掘进表现的研究水平对盾构选型设计、施工掘进效率预测等具有重要意义，一直以来受到许多学者^[1-7]的广泛关注。朱合华等^[1]建立了土体-盾构机相似系统，对软土地层进行了相似模型试验研究，提出了包含盾构施工参数及地层物理力学参量的地层适应性理论。邢彤等^[2]指出在盾构装备系统设计时，需要预测盾构在不同土层掘进时的刀盘功率，发现刀盘剪切力矩和搅动力矩共占总刀盘扭矩的99%。施虎等^[4]进一步建立了盾构推进分项阻力计算模型，利用盾构模拟系统研究发现土压力在推进力计算中发挥了关键性作用，并确定了由土压力与切深率组成的推进力计算模型。赵博剑等^[6]以深圳地铁复合式土压平衡盾构施工为背景，对区间典型地层的盾构掘进参数与地层相关性进行了统计分析，发现不同地层中的施工参数存在一定波动差异性。陈仁朋等^[7]对盾构掘进中盾构与围岩的相互作用规律、土压平衡盾构总推力、刀盘扭矩的影响因素进行了分析，研究结果可用于盾构刀盘装备扭矩设计等。在盾构施工参数对地层位移影响方面，郑刚等^[8-9]分析了盾构推进参数与掘进速度的关系，并研究了对周围地层沉降的影响规律，发现当掘进速度不同时各掘进关键参数的取值范围不同，但各掘进参数之间具有一定的相关性。魏新江等^[10]通过盾构隧道施工现场监测，研究了盾构参数关系及其对地层位移的影响，发现盾构总推力、土舱压力和刀盘扭矩基本同步变化，施工沉降与土舱内外压力差值成反比。综上可知盾构在不同土层中的施工参数具有一定差异性，而这种差异性在盾构的选型设计、施工控制及扰动影响研究中均不能忽视；同时，在掘进参数分析方面主要以单一指标变化为主，基于土压平衡盾构施工参数的多参量评价指标和预测方法还较少。另外，对EPB盾构掘进表现的研究可以从理论、试验和数值分析等方面进行，但就实际应用而言，现阶段以盾构施工自动记录数据为资源，利用数理统计方法对盾构机-地层空间关系进行辨识不失为一种有效方法，并且随着大数据技术的兴起，将为海量盾构施工参数分析、盾构掘进表现预测及智能优化控制提供技术支撑。目前，长沙地下轨道交通和市政管廊建设数量快速增长，带动了大量EPB盾构工程出现，现有研究^[11-12]发现长沙地层条件较复杂，具有一定的代表性，因而，本文作者对其典型地层的EPB盾构掘进参数进行统计研究，分析探讨盾构施工地层的可掘性，提出具有一定适用性的掘进表现预测模型，以便为本地乃至全国范围内类似地层的EPB盾构施工和研究提供参考。

1  工程概况

1.1　工程背景

长沙市某盾构工程为湖南省首条采用土压平衡盾构施工的电力管廊隧道，盾构全长约6.0 km。隧道内径为3.6 m，衬砌管片宽度分别为1.2 m和1.0 m。本电力盾构隧道工程采用2台中铁山河土压平衡盾构机掘进施工，盾构机主要设备参数见表1。

表1　土压平衡盾构机设备参数

Table 1　Equipment parameters of EPB shield machine

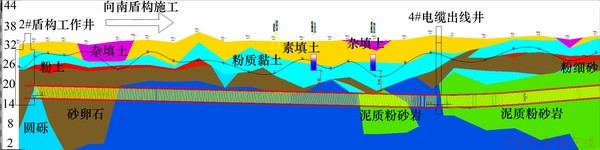
图1　盾构隧道典型地层工程地质图

Fig. 1　Engineering geological map of typical strata of shield tunnel

1.2　工程水文地质条件

根据现场勘测情况，该盾构隧道工程场地地层由第四系地层与基岩组成。地质条件复杂，隧道从南向北盾构掘进面先后经过砾岩、砂卵石、泥岩、圆砾、板岩、粉质黏土等地层，其中主要为砾岩、砂卵石和泥岩地层。本标段第四系覆盖层有全新统填土、粉质黏土、粉土等；上更新统白水江组冲积粉质黏土、粉细砂、圆砾、卵石等；中更新统马王堆组冲积粉质黏土、圆砾、卵石以及残积粉质黏土等；基岩有白垩系泥岩、砾岩、以及板岩。场地地下水位稳定水位埋深在0.4～17.4 m之间变化，水位标高在22.57～59.49 m之间变化。

2  EPB盾构施工参数统计及分析

为对长沙典型地层EPB盾构施工参数进行分析，根据地勘报告在工程现场分别调取、读存砾岩、砂卵石和泥岩(泥质粉砂岩) 3类地层，合计147环盾构机施工在线自动保存数据。其中，盾构机数据的自动保存频率为1次/s，而本次以1次/(3 s)调取数据，并用于分析。盾构隧道典型地层工程地质图见图1。

2.1　典型地层EPB盾构主要施工参数变化特征

2.1.1　贯入度　

对土压平衡盾构而言，评价刀盘工作表现的关键指标为贯入度P_rev，其物理意义为刀盘每转下的刀盘切入深度，定义式如下：

(1)

式中：P_rev为贯入度，mm/r；v为盾构机推进速度，mm/min；N为刀盘转速，r/min。

贯入度在一定意义上表征了盾构施工地层的可掘性和机械作业水平。本文分别统计分析3类地层的贯入度，结果如图2所示。从图2可见：贯入度在3类典型地层中具有鲜明的分布特征，其均值分别为33.96，40.97和20.48 mm/r，在砂卵石地层中最大，泥岩地层中最小，即在泥岩地层中盾构掘进表现水平较低，这可能与地层的细颗粒含量或液性、塑性相关。砂卵石地层的贯入度变化幅度较大，说明盾构机施工时的表现水平稳定性较差。需说明的是，由式(1)定义的贯入度主要用于评价刀盘与土的接触状态，不能片面理解为降低刀盘转速可以提高贯入度。从极限角度考虑，当刀盘转速很低时，刀盘处于非转动状态，则作用于土体的切向力作用同步降低，此时，单纯依靠增大推进力难以提高贯入度。贯入度在土体中的表现主要应受地层条件如地层的含泥量的影响。在室内对3类典型地层含泥量进行抽样分析，发现砾岩、砂卵石和泥岩地层的含泥量分别为27.2%，7.80~10.01%和25.10~33.05%。对于盾构机的实际掘进速度v而言，这3种地层的推进速度和贯入度关系均可表达为线性函数，说明通过提高贯入度可以加快盾构掘进速度。由贯入度的定义可知，推进速度和贯入度的比值其实质为刀盘转速，且经图2拟合分析后，也可以看出线性函数的斜率基本接近各地层刀盘转速的均值，说明盾构机在3类典型地层掘进过程中其刀盘转速基本恒定。本工程中砾岩、砂卵石和泥岩地层中的刀盘转速均值分别为1.83，1.22和1.66 r/min，砂卵石地层的低转速设定与现场施工为保证刀盘扭矩具有一定的富余量有关；另外，对盾构掘进扰动敏感的砂卵石地层而言，不同刀盘转速产生的振动扰动效应控制也是需要注意的关键问题。

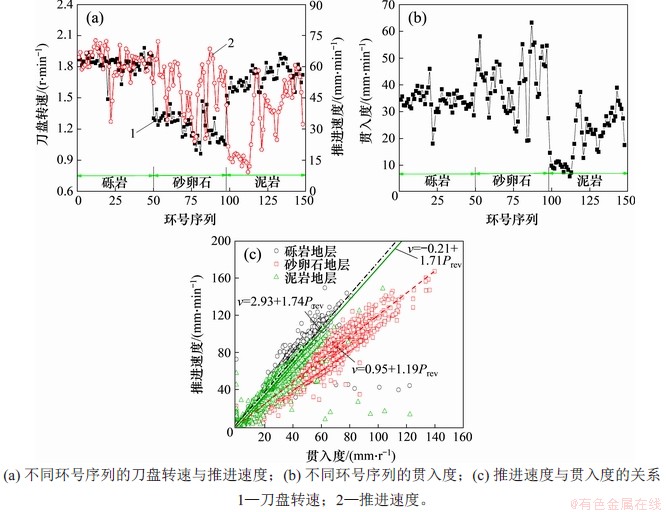
图2　典型地层EPB盾构贯入度及相关参数变化曲线

Fig. 2　Change curves of penetration and related parameters of EPB shield in typical stratum

2.1.2　刀盘扭矩、螺机扭矩和土仓压力　

典型地层刀盘扭矩、螺机扭矩及土仓压力变化曲线如图3所示。从图3可见：在3类典型地层中，刀盘扭矩不尽相同，在砾岩地层中刀盘扭矩较稳定，而在砂卵石和泥岩地层中具有显著的震荡性，这可能与砂卵石和泥岩地层的颗粒级配、风化程度等有关，这类特征在螺机扭矩的变化中依然存在，而两者共同对土仓压力产生影响。3种地层土仓压力均值表明典型地层依然具有鲜明的地层属性。其中，砂卵石地层的土仓压力最大，均值达到1.48×10⁵ Pa，砾岩地层最小为0.39×10⁵ Pa，说明盾构在砂卵石地层掘进施工时，受砂卵石地层土水压力平衡和失稳控制需要，其土仓压力通常较大。盾构机的刀盘扭矩分布曲线因地层不同而有所差异，刀盘扭矩在泥岩地层中分布范围最广，均值达1 005.14 kN·m；砂卵石地层的扭矩分布较广，且在300~1 200 kN·m之间分布较均匀；而砾岩地层中刀盘扭矩以均值950.37 kN·m为中心，分布较集中，其标准差最小，说明刀盘在砾岩地层的工作状态较稳定。

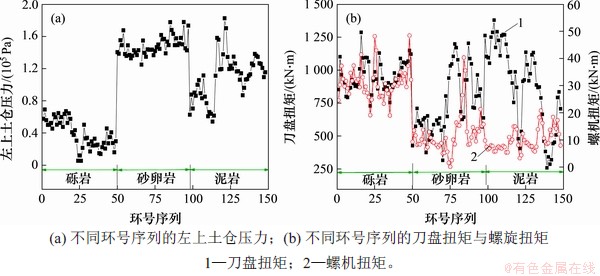
图3　典型地层刀盘扭矩、螺机扭矩及土仓压力变化曲线

Fig. 3　Variation curves of torque of cutterhead, torque of screw conveyor and earth bin pressure in typical stratum

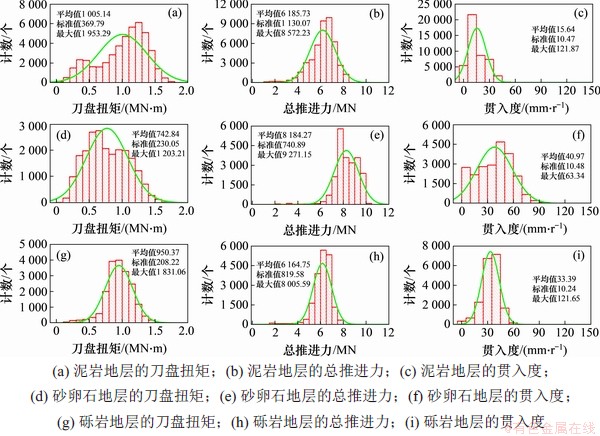
图4　典型地层土压平衡盾构相关参数统计直方图

Fig. 4　Statistical histograms of related parameters of EPB shield in typical stratum

2.1.3　总推进力及与刀盘扭矩关系　

典型地层土压平衡盾构相关参数统计直方图如图4所示。从图4可以看出盾构机的总推进力因地层不同，在分布曲线上存在一些特点：总推进力在3类地层中的分布普遍较集中，泥岩和砾岩地层的分布特征及数值较接近，且均低于砂卵石地层的总推进力，这与砂卵石地层的土仓保压有关；对于宽级配的砂卵石地层，维持掌子面的稳定性是施工中的一个关键问题，因而，需要保证一定的推进压力，这从图3所示的土仓压力均值可以看出，均远大于其他2类地层的土仓压力。

EPB盾构总推进力与刀盘扭矩的关系见图5。从图5可见：刀盘扭矩整体上随总推进力提高而增大，但在3种地层中，两者的线性拟合相关性不同，泥岩地层的拟合度最高为0.64。在泥岩地层中施工时应合理把握盾构总推进力，防止过荷挤压刀盘，造成其超荷工作。

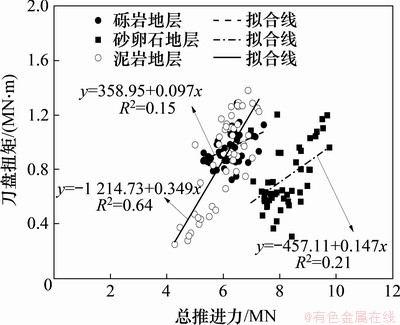
图5　典型地层盾构刀盘扭矩和总推进力变化曲线

Fig. 5　Change curves of cutterhead torque and total total thrust of shield in typical stratum

2.2　典型地层EPB盾构装备系数取值

在EPB盾构的选型设计中涉及1个关键问题：如何合理确定盾构机的装备总推进力和刀盘扭矩^[2,4,7]。相关模型(见式(2)和(3))可用于解决这个问题，同时，结合本工程盾构刀盘直径为4.35 m，根据实际推力和刀盘扭矩反算3类地层的相关经验系数，结果如表2所示。

(2)

(3)

式中：F为盾构机装备油缸千斤顶推力，kN；T为刀盘装备扭矩，kN·m；D为盾构机刀盘(开挖)直径，m；α和β分别为盾构机装备系数，其中α取14~23，β取500~1 200。

从表2可以看出：3类地层中盾构刀盘扭矩系数α的最大值(17)出现在泥岩地层中，且位于经验值范围内；而总推进力系数β在砂卵石地层中达到最大值514，其余地层均远低于经验值。这说明在土压平衡盾构中，当(砾岩、泥岩)地层的自稳性增强时，总推进力将低于同直径TBM机械参数取值。β的差异现象与TBM和EPB盾构的机械作业特点相关，在TBM施工中推进力施加于刀盘的压力对破碎、切削岩石具有一定作用^[13-14]；而对EPB盾构主要面对的软岩和土类地质而言，只有在如同砂卵石可能含有大量大颗粒岩石或风化程度较低的地层中需要推进力的挤压作用之外，软岩和土类地层主要靠刀盘的作功实现开挖掘进，总推进力的作用功能下降。因而，针对长沙典型地层而言，建议EPB盾构总推进力的装备系数可按相同刀盘直径TBM的经验系数进行一定折减，而对于不同直径的EPB盾构有待进一步研究确定。

表2　典型地层EPB盾构机装备系数统计

Table 2　Statistics of EPB shield machine equipment coefficient in typical stratum

3  EPB盾构掘进表现及预测

3.1　EPB盾构掘进典型地层可掘性分析

从上述分析结果可以看出，盾构机总推进力、刀盘扭矩与贯入度存在关联，但从各参数的单一变化很难充分说明EPB盾构施工参数在各地层中的统一变化规律。据式(4)定义的归一化的总推进力-场切入指数I_FP为

(4)

式中：I_FP为场切入指数，kN/(mm·r^-1)；F为盾构机推进力，kN；P_rev为贯入度，mm/r。

从图6可以看出：无论是单个地层(图6(b)所示为泥岩地层施工参数，砾岩和砂卵石地层变化特征与其相似)，或是3类地层各环施工参数的均值统计结果，场切入指数与贯入度具有高度的关联性，可以用下列幂函数表示二者之间的关系：

(5)

场切入指数随贯入度的增大而减小，当贯入度小于20 mm/r时，场切入指数变化范围较大；而当贯入度大于一定值时，场切入指数的变化范围减小。需要指出的是，图6(a)所示的第615环开挖全过程中，在盾构开挖伊始和中途停顿复开之时，贯入度极小，而I_FP成倍增加，远高于其正常掘进阶段的均值，因而，目前在描述各地层EPB盾构施工参数时以其均值进行分析较合适(结果如图6(c)所示)，但合理的取值标准应该通过更科学的统计方法予以解决。进一步，I_FP和贯入度变化曲线显示出鲜明的地层聚类特征，泥岩地层I_FP变化范围最大，且其贯入度主要分布于40 mm/r以内，这与本项目泥岩地层的盾构实际施工情况基本相符，泥岩地层的整体开挖进度比其他2类地层的慢。理论上，EPB盾构施工中贯入度越大，开挖速度越快，贯入度在一定程度上表征了地层可掘进的难易程度。I_FP与贯入度保持了高度关联的变化关系，又联系了地层与EPB盾构的工作状态，因而，建议将I_FP作为表示EPB盾构施工地层可掘性的另一个指标。

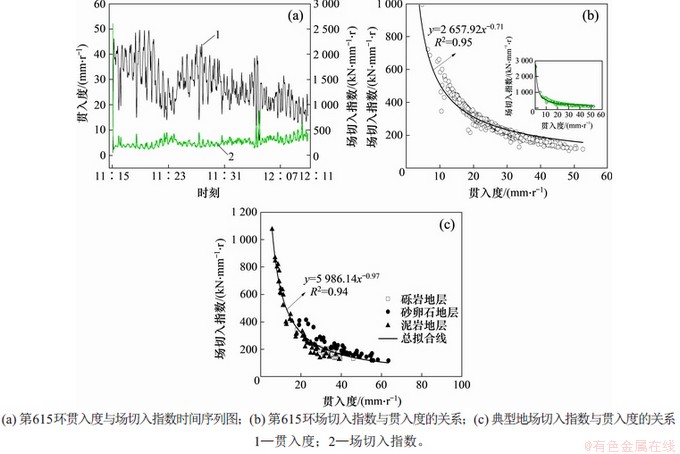
图6　EPB盾构场切入指数与贯入度变化曲线

Fig. 6　Change curves of field penetration index and penetration of EPB shield

3.2　典型地层EPB盾构掘进表现及地层可掘性

3.2.1　典型地层掘进比能　

国内外研究者对TBM掘进表现预测提出了一些方法，其核心是联合计算确定岩层的掘进比能，即TBM掘进单位体积岩土体所消耗的能量。掘进比能(忽略推进力做功)的定义式如下：

(6)

代入式(1)，并化简整理，得

(7)

式中：E_S为掘进比能，kW·h/m³；N为刀盘转速，r/min；T为盾构刀盘扭矩，kN·m；D为盾构机刀盘(开挖)直径，m；v为盾构推进速度，mm/min。P_rev为盾构刀盘贯入度，mm/r。

掘进比能在实际计算或测试中可以通过室内全尺寸试样切削试验和现场TBM掘进参数按照式(6)计算得到，且二者之间满足一定关系。例如，按照室内全尺寸岩石切削试验获得的比能在EPB盾构掘进土质地层时应乘以1个提高系数，文献[15]在考虑土仓压力的存在和影响条件下建议取值1.8。通常将掘进比能与贯入度联合进行分析，以确定最优贯入度，结果如图7所示。从图7可以看出掘进比能随贯入度增大而降低，可以由下列幂函数表示两者关系：

(8)

式(8)表明EPB盾构刀盘每转情况下切入土体的深度增加，则切削开挖单位体积土体所消耗的能量越少，掘进速度将得到同步提高；同时，对于本工程而言，砾岩和砂卵石的掘进比能大多数低于5 kW·h/m³，而泥岩地层的掘进比能为1.03~24.04 kW·h/m³，其均值为7.25 kW·h/m³；砾岩和砂卵石地层掘进比能均值分别为3.35 kW·h/m³和2.30 kW·h/m³。因而，从EPB盾构掘进能量角度看，泥岩地层依然为EPB盾构施工的低效能地层，需要注意渣土改良。

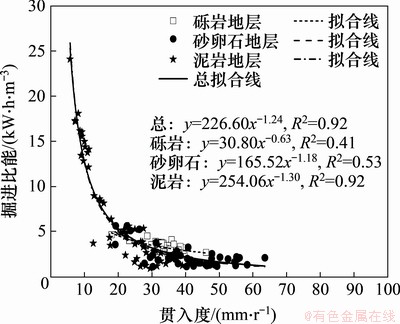
图7　典型地层掘进比能-贯入度变化曲线

Fig. 7　Change curves of specific energy and penetration in typical strata

3.2.2　EPB盾构地层可掘性讨论　

典型地层掘进比能-场切入指数变化曲线如图8所示。从图8可以看出：掘进比能E_S与场切入指数I_FP高度相关，即E_S随I_FP增大呈线性增大，其中，砾岩和砂卵石地层的E_S和I_FP变化范围较小，而泥岩分布较广，再次说明EPB盾构在3类典型地层中掘进施工的难易性；贯入度、场切入指数和掘进比能这3个指标相关性较好，完全满足实际工程应用的计算精度要求。这里研究这3个指标内在的物理力学机制。谭卓英^[16]根据岩石可钻性的定义，认为表征岩石可钻性的指标大体上可归纳为位移指标、强度指标和能量指标，其中，位移指标用穿孔速率、钻头进尺和贯入度等表示，强度指标用抗压强度、点荷载强度等表示，能量指标用凿碎比功(破碎凿进单位体积或进尺所消耗的能量)表示。本文采纳的TBM中广泛应用的的掘进比能E_S其实质就是能量指标，因此，本文在EPB盾构掘进表现计算中采纳的贯入度、场切入指数及掘进比能三者均可作为表征土体可掘性的指标，它们之间具有高度的相关性。同时，强度指标I_FP和能量指标E_S分别由土压平衡盾构的推进系统和刀盘系统的参数计算而得，其结果的相关性充分说明采用盾构施工参数表示土层界面特性的科学性，这将为土压平衡盾构机-岩土的工作空间状态映射识别研究提供有力支撑。而需要注意的是，在岩石可掘性或TBM施工参数指标(如掘进比能E_S)研究中，岩石的节理、完整性等通常对计算结果产生较大影响。对于EPB盾构而言，其掘进地层的类别、风化程度、颗粒级配和液塑限^[17]等都可能对其指标计算产生影响，如本文中泥岩地层的施工参数受风化程度等影响，其数值范围较大(1.11~24.15 kW·h/m³)，而上述问题的解决都将为EPB盾构的施工表现预测和性能优化进一步提供依据。

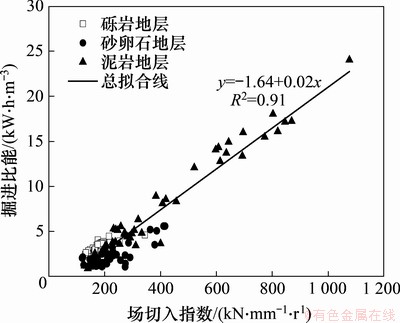
图8　典型地层掘进比能和场切入指数变化曲线

Fig. 8　Change curves of specific energy and field penetration index in typical strata

3.3　典型地层EPB盾构掘进表现预测

在确定计算掘进比能后，可以通过下式计算净掘进速率：

(9)

式中：R_NP为净掘进速率，m³/h；k为能量转化率，在TBM中建议取值0.80~0.90；N为盾构刀盘转速，r/min；T为盾构刀盘扭矩，kN·m。

根据式(9)计算R_NP时，需要先确定能量转化率k，但目前未见EPB盾构施工的建议值，而EPB盾构中土仓压力的存在和变化都可能对能量的转化产生影响，为此，本文根据式(10)由每环开挖平均速度估算3类地层的R_NP，结果如图9所示。

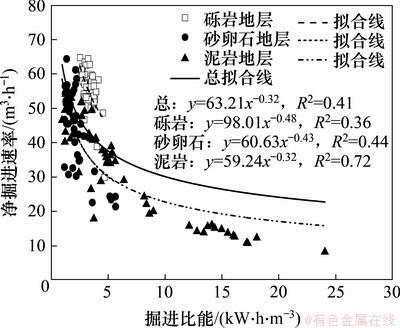
图9　典型地层净掘进速率-掘进比能变化曲线

Fig. 9　Change curves of net penetration rate and specific energy in typical strata

(10)

需要说明的是，根据式(10)计算的R_NP在数学表达上等同于式(9)中的R_NP(k=1)，其原因是：式(6)和(9)中的2πNT实质上是将全部刀盘驱动能量视为掘进土体的净能量，即“考虑”了能量转化后的掘进土体能量。但事实上，刀盘的一部分能量用于克服自身机械结构摩擦、土仓渣土搅拌和侧面摩擦等而被消耗，如式(11)计算掘进土体的净刀盘扭矩T_net应该为总刀盘扭矩T乘以能量转化率k，因而，严格的掘进比能E_S-net定义和R_NP计算公式分别为式(12)和式(13)。所以，需要指出本文根据式(6)计算的掘进比能E_S要比真实值E_S-net大。

(11)

(12)

(13)

从图9可以看出：3类地层的R_NP基本都随掘进比能增大而降低，但总拟合线相关系数低于砂卵石地层和泥岩地层各自的拟合相关系数，数据点偏离拟合线的范围较广，特别是当掘进比能低于5 kW·h/m³时，砂卵石的R_NP远在总拟合线之下，这或与EPB盾构在3种地层中的实际能量转化率有关。因而，在计算确定不同地层的EPB盾构净掘进速率时，应该通过进一步研究解决(考虑土仓压力、地层条件)EPB盾构能量转化率的取值以及EPB盾构施工地层掘进比能确定计算问题，文献[15]给出了1个参考方法。

净掘进速率R_NP和贯入度变化关系如图10所示。从图10可以看出：R_NP随着贯入度增大而增大。但仍然存在如下问题：3种地层中砂卵石与其他2类地层的数据点趋近性较差，较离散，致使总拟合线的相关系数比3个地层的相关系数低。若将砾岩和泥岩地层的数据点统一拟合，则其相关系数达0.97(见图10中y′拟合方程)，而砂卵石地层的相关系数为0.83。因此，建议在实际分析和应用中，将砾岩和泥岩地层归为一类，采用共同拟合公式；而砂卵石使用其本身的拟合公式。

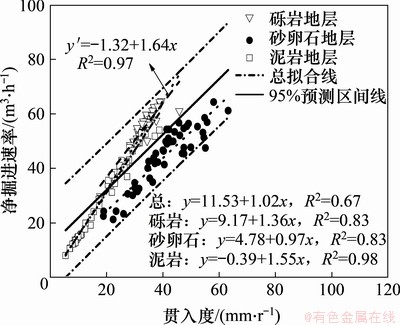
图10　典型地层净掘进速率-贯入度变化曲线

Fig. 10　Change curves of net penetration rate and penetration in typical strata

(14)

同时，场切入指数与净掘进速率之间的关系如图11所示。从图11可见：场切入指数与净掘进速率之间保持了较好的一致性和相关性(关系式见式(15)，R²=0.88)，说明用场切入指数预测EPB盾构在地层中的净掘进速率具有显著的确定性。

(15)

在确定净掘进速率后，最终的预测目标是估计EPB盾构的日掘进速率R_DP。在实际施工中，除了机械开挖土体的环节外，还包括管片拼装、渣土运输、铺设轨道、机械维修保养等环节，因而，通过R_NP计算R_DP的前提是预估每天用于掘进开挖环节的利用率。文献[18]通过不同工程的施工记录和经验，提出了机械利用时间率T_MU，从而R_DP的预测值最终可以根据下式计算求得：

(16)

式中：R_DP为日掘进速率，m/d；T_MU为机械利用时间率，取25%~45%；m³/h；h为每日工作时间，h/d；D为盾构直径，m。

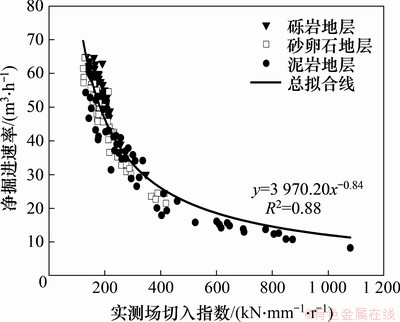
图11　典型地层净掘进速率和场切入指数变化曲线

Fig. 11　Change curves of net penetration rate and field penetration index in typical strata

对EPB盾构掘进表现预测流程如下：首先通过式(5)计算特定地层的场切入指数I_FP，然后根据式(15)计算其对应的净掘进速率R_NP，并最终换算成日掘进速率R_DP。当然，上面提到的根据式(14)以贯入度分类计算R_NP也是一种有效方法。需要指出的是，最终所有的问题都聚焦于本文研究的施工参量，即贯入度P_rev。应该结合TBM掘进岩石所采用的室内全尺寸岩石样切削试验确定最优贯入度的方法，或者通过岩土体单轴压缩强度(UCS)试验计算室内掘进比能，并结合现场EPB盾构掘进数据确定每类地层的对应换算系数，上述问题都将是进一步研究重点。

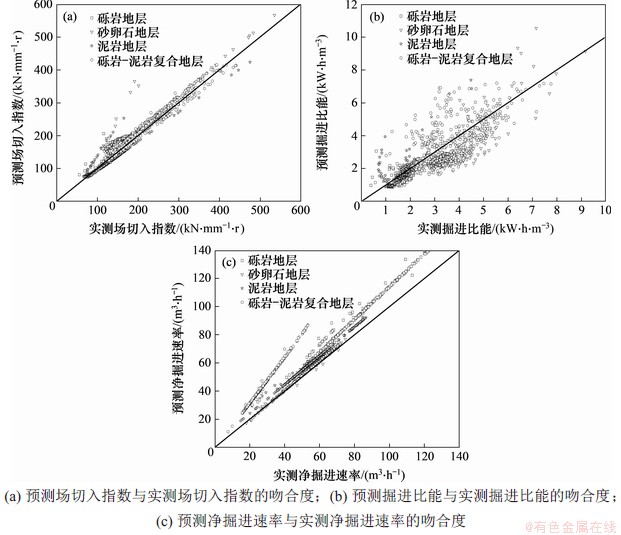
图12　各经验模型参数预测值与实测结果对比曲线

Fig. 12　Comparison of predicted values and measured results of each empirical model parameters

3.4　预测模型实例验证

为对上述预测经验模型进行验证，在工程现场根据勘查报告又分别调取砾岩、泥岩、砂卵石以及泥岩和砾岩组成的复合地层4类地层作为模型适用性检验案例。调取的4种地层条件盾构施工数据为盾构开挖每环宽进尺的全过程数据，预测对比分析结果如图12所示。从图12可以看出：1) 根据式(5)由贯入度预测的场切入指数与实测值一致性最高，除盾构启动瞬间的部分数据点离散外，基本上所有数据点都位于y=x这条线上；2) 根据贯入度预测掘进比能，砂卵石和砾岩地层的吻合度最高，而泥岩预测值小于实测值，这可能与本环地层的风化程度有关；3) 根据式(15)计算的净掘进速率与实测值对比，除泥岩地层预测结果与实测结果一致之外，其余3个地层的预测值高于实测值，这或与实测的3种地层的能量转化率较低有关。从图11可知拟合线趋势和拟合公式(15)受泥岩地层施工数据的影响严重，因而泥岩地层的预测效果最好。总体而言，本文所统计分析提出的预测EPB盾构施工掘进表现各经验模型具有一定适用性，可为长沙及国内相似地质EPB盾构施工和研究提供参考。

4  结论

1) 贯入度等参数的分布具有一定的地层聚类特征。刀盘扭矩和螺机扭矩在砂卵石和泥岩地层中呈现一定的震荡性，在砾岩地层中较稳定。因地层失稳控制需要，砂卵石地层的EPB盾构土仓压力显著比其他2类地层的高，并导致其总推进力同步增大，而总推进力的增大又不同程度地引起刀盘扭矩增加。

2) 场切入指数和掘进比能均随贯入度增大而减小，同时，掘进比能随掘进比能增加而呈线性提高，这3者间相关性较好，可以表征地层的可掘性。这3个指标在泥岩地层的分布范围较大，而在砾岩和砂卵石地层中分布较集中。EPB盾构在泥岩地层掘进时需注意渣土改良。

3) 净掘进速率随掘进比能和场切入指数增大而降低，随贯入度增大而提高。对不同地层刀盘作功能量转化率的分析计算对净掘进速率预测模型的应用至关重要。4类地层的EPB盾构掘进表现预测验证了所提出的代表性模型的适用性。

参考文献：

[1] 朱合华, 徐前卫, 傅德明, 等. 地层适应性盾构模型试验设计方法初探[J]. 岩土力学, 2006, 27(9): 1437-1441.

ZHU Hehua, XU Qianwei, FU Deming, et al. Study on design principle of shield machine applicable to different strata[J]. Rock and Soil Mechanics, 2006, 27(9): 1437-1441.

[2] 邢彤, 龚国芳, 杨华勇. 盾构刀盘驱动扭矩计算模型及实验研究[J]. 浙江大学学报(工学版), 2009, 43(10): 1794-1800.

XING Tong, GONG Guofang, YANG Huayong. Torque calculation model of cutting head in shield machine and experimental study[J]. Journal of Zhejiang University (Engineering Science), 2009, 43(10): 1794-1800.

[3] 邢彤. 盾构刀盘液压驱动与控制系统研究[D].杭州: 浙江大学机械工程学院, 2008: 98-123.

XING Tong. Research on hydraulic drive and control system of the cutter head in shield tunneling machine[D]. Hangzhou: Zhejiang University. School of mechanical engineering, 2008: 98-123.

[4] 施虎, 龚国芳, 杨华勇, 等. 盾构掘进机推进力计算模型[J]. 浙江大学学报(工学版), 2011, 45(1): 126-131.

SHI Hu, GONG Guofang, YANG Huayong, et al. Determination of thrust force for shield tunneling machine[J]. Journal of Zhejiang University(Engineering Science), 2011, 45(1): 126-131.

[5] 江华, 江玉生, 张晋勋, 等. 北京地铁砂卵石地层土压平衡盾构施工刀盘扭矩研究[J]. 中国铁道科学, 2013, 34(3): 59-65.

JIANG Hua, JIANG Yusheng, ZHANG Jinxun, et al. Research on cutterhead torque during earth pressure balance shield tunneling in sand gravel strata of Beijing Metro[J]. China Railway Science, 2013, 34(3): 59-65.

[6] 赵博剑, 周建军, 谭忠盛, 等. 复合地层盾构掘进参数及其与地层相关性分析[J]. 土木工程学报, 2017, 50(S1): 140-144.

ZHAO Bojian, ZHOU Jianjun, TAN Zhongsheng, et al. Variation of shield boring parameters and correlation analysis in mixed ground[J]. China Civil Engineering Journal, 2017, 50(S1): 140-144.

[7] 陈仁朋, 刘源, 汤旅军, 等. 复杂地层土压平衡盾构推力和刀盘扭矩计算研究[J]. 地下空间与工程学报, 2012, 8(1): 26-32.

CHEN Renpeng, LIU Yuan, TANG Lüjun, et al. Research on calculation of thrust and cutter head torque on shield in complex strata[J]. Chinese Journal of Underground Space and Engineering, 2012, 8(1): 26-32.

[8] 郑刚, 路平, 曹剑然. 基于盾构机掘进参数对地表沉降影响敏感度的风险分析[J]. 岩石力学与工程学报, 2015, 34(S1): 3604-3612.

ZHENG Gang, LU Ping, CAO Jianran. Risk analysis based on the paramenters sensitivity analysis for ground settlement induced by shield tunneling[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(S1): 3604-3612.

[9] 张恒, 陈寿根, 邓稀肥. 盾构掘进参数对地表沉降的影响分析[J]. 现代隧道技术, 2010, 47(5): 48-53.

ZHANG Heng, CHEN Shougen, DENG Xifei. Analysis of the influence of shield driving parameters on groud settlements[J]. Modern Tunneling Technology, 2010, 47(5): 48-53.

[10] 魏新江, 周洋, 魏纲. 土压平衡盾构掘进参数关系及其对地层位移影响的试验研究[J]. 岩土力学, 2013, 34(1): 73-79.

WEI Xinjiang, ZHOU Yang, WEI Gang. Research of EPB shield tunneling parameter relations and their influence on stratum displacement[J]. Rock and Soil Mechanics, 2013, 34(1): 73-79.

[11] 胡焕校, 杨万松, 孙端阳. 长沙板岩地层地铁盾构施工渣土改良试验研究[J]. 水文地质工程地质, 2018, 45(4): 100-107.

HU Huanxiao, YANG Wansong, SUN Duanyang. Soil conditioning test for EPB shield tunneling in slate stratum in the Changsha region[J]. Hydrogeology ＆ Engineering Geology, 2018, 45(4): 100-107.

[12] 肖超, 阳军生, 褚东升, 等. 长沙地铁典型板岩地层土压平衡盾构掘进参数精细化控制[J]. 中南大学学报(自然科学版), 2015, 46(1): 261-266.

XIAO Chao, YANG Junsheng, CHU Dongsheng, et al. Detailed control for shield excavation parameters in typical slate strata of Changsha Metro[J]. Journal of Central South University (Science and Technology), 2015, 46(1): 261-266.

[13] ZHANG Q, HUANG T, HUANG G Y, et al. Theoretical model for loads prediction on shield tunneling machine with consideration of soil-rock interbedded ground[J]. Science China(Technological Sciences), 2013, 56(9): 2259-2267.

[14] GONG Q M, ZHAO J, JIANG Y S. In situ TBM penetration tests and rock mass boreability analysis in hard rock tunnels[J]. Tunnelling and Underground Space Technology, 2007, 22: 303-316.

[15] NAMLI M, BILGIN N. A model to predict daily advance rates of EPB-TBMs in a complex geology in Istanbul[J]. Tunnelling and Underground Space Technology, 2017, 62: 43-52.

[16] 谭卓英. 岩土工程界面识别理论与方法[M]. 北京: 科学出版社, 2008: 50-52.

TAN Zhuoying. Theory and method of interface identification in geotechnical engineering[M]. Beijing: Science Press, 2008: 50-52.

[17] AVUNDUK E, COPUR H. Empirical modeling for predicting excavation performance of EPB TBM based on soil properties[J]. Tunnelling and Undergroud Space Technology, 2018, 71: 340-353.

[18] COPUR H, AYDIN H, BILGIN N, et al. Predicting performance of EPB TBMs by using a stochastic model implemented into a deterministic model[J]. Tunnelling and Underground Space Technology, 2014, 42: 1-14.

（编辑  陈灿华）

收稿日期： 2019 -10 -25; 修回日期： 2020 -01 -08

基金项目(Foundation item)：国家自然科学基金资助项目(51478484, 51778641)(Projects(51478484, 51778641) supported by the National Natural Science Foundation of China)

通信作者：张沛然，博士研究生，从事岩土工程、隧道及地下工程研究；E-mail:zhangpr91@163.com