基于敏感模态单元应变能法结构损伤识别
张效忠1, 2,姚文娟1
(1. 上海大学 土木工程系,上海,200072;
2. 衢州学院 建筑工程学院,浙江 衢州,324000)
摘要:根据结构损伤前后特征值变化率选择对损伤单元应变能变化灵敏度较高的模态,建立一种高效的并具有较好鲁棒性的结构损伤识别的方法。从结构振动方程出发,推导结构损伤前后特征值变化率和应变能变化的关系式,建立一个由特征值变化率、单元损伤因子、单元损伤灵敏度因子以及单元损伤修正因子组成的结构损伤识别方程。应用单元损伤修正因子建立结构的损伤定位指标,并应用结构损伤识别方程式推导出单元损伤程度因子的解析表达式。应用本方法对一新型防浪提结构进行单一处损伤和多处损伤的损伤位置识别和损伤程度识别,最后,对本文提出的损伤识别方法的抗噪声性能进行测试。研究结果表明:本方法具有较好的鲁棒性,并且识别结果具有较高的精度,表明本文提出方法具有高效性。
关键词:特征值变化率;单元应变能;结构损伤识别方程;鲁棒性
中图分类号:O327;TU33;TV92 文献标志码:A 文章编号:1672-7207(2013)07-3014-10
Structural damage identification using element strain energy method based on sensitive modals
ZHANG Xiaozhong1, 2, YAO Wenjuan1
(1. Department of Civil Engineering, Shanghai University, Shanghai 200072, China;
2. School of Architectural Engineering, Quzhou University, Quzhou 324000, China)
Abstract: According to the rate of change of eigenvalues of undamaged and damaged structure, modals with higher sensitivity for the damage element strain energy change were selected. Based on this, an efficient structural damage identification method with better robustness was established. Starting from the structural vibration equation, the relationship between the rate of change of the eigenvalue and strain energy changes before and after structural damage was derived. A structural damage identification equation consisted of the rate of change of a characteristic value,the element damage factor, element damage sensitivity factor and element damage correction factor was built. A damage location indicator of structure was established by applying the element damage correction factor and an analytical expression of the element damage factor was derived using structural damage identification equation. The proposed method was applied to a new shell breakwater structure to identify the location and degree of damage, including a single damage and multiple damage. Finally,the noise immunity of the proposed damage identification method was tested. The results show that this method has better robustness and high accuracy recognition results, which shows that the proposed method has a high efficiency.
Key words: rate of change of eigenvalues; element strain energy change; structural damage identification equation; robustness
基于动力特性的结构的损伤识别的核心是选取一个易测、对结构损伤敏感的参数。而选择的敏感参数必须满足2个基本条件[1]:(1) 对局部损伤敏感;(2) 为位置坐标的函数。固有频率和单元模态应变能是结构损伤识别常用的2个敏感参数。当结构发生损伤后,可以通过结构损伤前后固有频率的变化率来识别结构的损伤。Lifshitz等[2]提出通过结构损伤前后频率的变化进行结构的损伤识别。Salawu[3]对利用固有频率的变化进行了综述。他认为损伤前后固有频率变化超过5%时结构基本上能判定发生损伤。但是,仅仅从固有频率的改变不能从模态改变的数据上判定结构的损伤。郑栋梁等[4]对基于固有频率变化的损伤识别技术的特点和方法进行了总结。Kim等[5-6]运用固有频率和模态在损伤前后的变化对一梁结构的损伤位置和程度进行了识别,并结合应变能方法对一不确定温度下的板梁桥进行了损伤识别。从本质上讲,结构的损伤引起的模态特征值的变化是由于结构的刚度发生变化,而刚度的变化能够从结构的固有频率变化来体现。Tomaszewska[7]认为在应用模态特性进行损伤识别时有可能由于损伤指标的问题使损伤识别结果精度不高甚至错误。朱宏平等[1, 4]对固有频率作为损伤指标的不足进行了总结,认为由于各阶固有频率对应的模态振型各处的模态应力状态都不相同,导致结构各阶固有频率对各处损伤的敏感性不同。各阶频率对同一位置的损伤敏感性不同,同一频率对各处损伤的敏感性也不同。而现阶段应用结构固有频率以及对应模态进行损伤识别时大多采用连续的有限的低阶频率及其对应的振型进行计算,这必然造成损伤识别精度不够或者不能够识别出结构的损伤。单元模态应变能法(EMSEM)是一种新的有前途的基于振动的损伤识别方法。Shi等[8]提出了单元模态应变能的概念,并得到结构损伤单元损伤前后的单元模态应变能变化率很大,而远离损伤单元的模态应变能变化率很小的结论。后期又将损伤前后单元模态应变能的变化率作为损伤定位的指标,分别对一平面桁架和框架结构的损伤进行了数值分析和试验研究[9]。王学广等[10]对单元模态应变能方法进行改进提高了结构损伤的识别精度。颜王吉等[11]把单元应变能变化灵敏度成功应用到结构的损伤识别中,提高了识别的效率。单元模态应变能法已成功地应用于桥[12]、板[13]和悬臂[14]等二维结构的损伤检测中。YANG等[15]在模态应变能的基础上创建了模态应变能分解方法,把模态应变能分解为轴向应变能和横向应变能,并建立2个方向的判定指标。LI等[16-17]应用模态应变能分解方法进行桁架结构的损伤识别,并把壳体结构转换为二维板结构进行损伤识别。这些方法本质仍是二维的结构损伤识别。目前还未见从理论方法上进行三维结构损伤识别的报道。由于三维结构受力和应变复杂,识别过程需要更高的灵敏度指标,所以,三维结构的损伤识别难度更大。在实际工程损伤识别过程中,受测量仪器、噪声以及手段的制约,现阶段常用的识别方法是在损伤识别的过程中应用连续的有限的低阶振型及相关参数进行损伤识别。但是,有些低阶模态对结构的损伤处并不敏感甚至产生负面影响,特别对于三维结构可能造成不能识别或者识别错误。因此,如何选择对结构损伤具有较高灵敏度的模态和损伤判别指标成为对三维结构损伤识别的关键因素。本文作者从结构的振动特征方程出发,推导结构振动特征值变化率和单元应变能变化的关系式,建立由特征值变化率、单元损伤程度因子、单元损伤灵敏度因子和单元损伤修正因子的方程式。提出敏感模态识别方法,在此基础上建立三维结构的损伤定位指标,并推导出三维结构损伤程度因子的解析表达式。最后,应用本文建立的三维结构损伤识别方法对某三维的海洋防浪堤结构进行单处和多处的损伤识别,验证所提出方法的正确性和适用性,并通过加噪声的方法验证本研究方法对结构的损伤识别的鲁棒性。
1 基本原理
根据结构动力学可知结构振动微分方程:
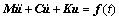 (1)
(1)
其中:M,C和K分别代表结构的质量矩阵、阻尼矩阵和刚度矩阵;u,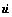 和
和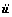 分别代表结构的位移向量、速度向量和加速度向量;f(t)代表结构的荷载向量,其特征值方程为
分别代表结构的位移向量、速度向量和加速度向量;f(t)代表结构的荷载向量,其特征值方程为
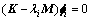 (2)
(2)
式中: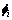 表示结构i阶模态的振型,为坐标x1,x2和x3的函数,即
表示结构i阶模态的振型,为坐标x1,x2和x3的函数,即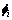
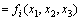 ;
;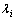 表示i阶模态的特征值,
表示i阶模态的特征值,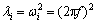 。
。
结构的损伤一般只是刚度降低,而结构的质量可认为不变,刚度变化可以用损伤前结构的刚度表达:
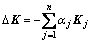 ;0≤
;0≤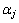 ≤1 (3)
≤1 (3)
其中: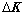 表示结构刚度的变化;
表示结构刚度的变化;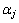 表示结构j单元损伤因子;
表示结构j单元损伤因子;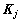 表示结构j单元损伤前的刚度矩阵;n代表结构有限元划分总的单元数。
表示结构j单元损伤前的刚度矩阵;n代表结构有限元划分总的单元数。
根据摄动理论,损伤后结构的特征值方程为
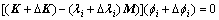 (4)
(4)
两边同时乘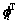 并展开得:
并展开得:
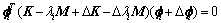 (5)
(5)
由式(2)两边同时乘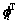 ,可以得:
,可以得:
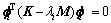 (6)
(6)
其中: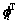 为结构i阶模态的振型的转置矩阵。将式(6)代入式(5)可得:
为结构i阶模态的振型的转置矩阵。将式(6)代入式(5)可得:
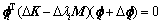 (7)
(7)
把式(7)展开得:
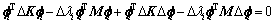 (8)
(8)
由式(2)变形可得:
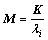 (9)
(9)
将式(9)代入式(8)得:
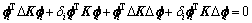 (10)
(10)
其中: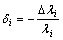 为结构特征值变化率,主要用于判断结构第i阶模态对结构损伤诊断的灵敏性。
为结构特征值变化率,主要用于判断结构第i阶模态对结构损伤诊断的灵敏性。
2 结构损伤识别方程
对于以抗弯为主的结构,结构单元模态势能可以由结构的单元模态应变能表示:
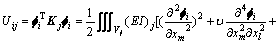
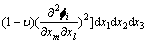 (11)
(11)
式中:Uij为结构i阶模态下j单元的单元应变能;(EI)j为结构j单元的抗弯刚度;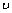 为泊松比;Vj为结构j单元的体积域;m=1, 2, 3;l=1, 2, 3
为泊松比;Vj为结构j单元的体积域;m=1, 2, 3;l=1, 2, 3 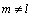 。令
。令
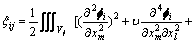
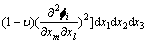 (12)
(12)
在单元足够小的情况下,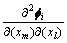 ,
,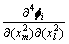 和
和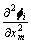 可以用j单元的节点的模态曲率取平均值得到,j单元的节点的模态曲率可以由结构的实测模态来确定。当结构单元划分足够小时,也可以认为结构的
可以用j单元的节点的模态曲率取平均值得到,j单元的节点的模态曲率可以由结构的实测模态来确定。当结构单元划分足够小时,也可以认为结构的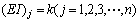 为定值,则有
为定值,则有
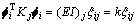 (13)
(13)
由式(3)和(13)可得:
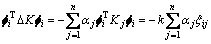 (14)
(14)
i阶模态结构的总的应变能为
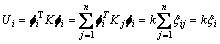 (15)
(15)
其中:
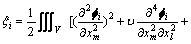
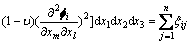 (16)
(16)
式中:V为整体结构的体积域。
由损伤前的表达式(13)可得结构发生损伤后i阶模态结构j单元势能:
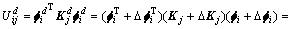
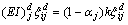 (17)
(17)
式中: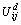 为损伤结构i阶模态下j单元的单元应变能;
为损伤结构i阶模态下j单元的单元应变能;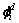 表示损伤后结构i阶模态的振型,是坐标x1,x2和x3的函数,即:
表示损伤后结构i阶模态的振型,是坐标x1,x2和x3的函数,即: ;
;
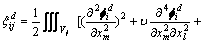
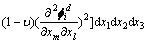
同样,在单元足够小的情况下,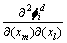 ,
,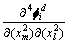 和
和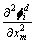 可以用j单元的节点的模态曲率取平均值得到,j单元的节点的模态曲率可以由结构的实测模态来确定。忽略高阶无穷小,将式(17)展开可得:
可以用j单元的节点的模态曲率取平均值得到,j单元的节点的模态曲率可以由结构的实测模态来确定。忽略高阶无穷小,将式(17)展开可得:
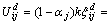
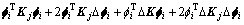 (18)
(18)
将式(3)和(13)代入式(18)可得:
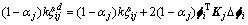 (19)
(19)
经整理可得:
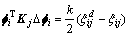 (20)
(20)
由式(20)可推得:
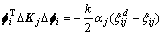 (21)
(21)
令
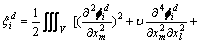
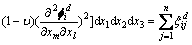 (22)
(22)
由式(20)和式(21)可得:
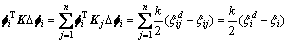 (23)
(23)
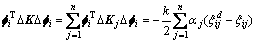 (24)
(24)
将式(14),(15),(23)和(24)代入式(10)可得:
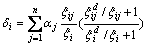 (25)
(25)
令
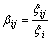 (26)
(26)
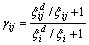 (27)
(27)
则式(25)可以变成:
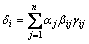 (28)
(28)
式中: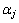 为单元损伤程度因子,0≤
为单元损伤程度因子,0≤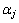 ≤1,
≤1,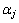 =1表示完全损伤,
=1表示完全损伤,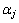 =0表示未损伤;
=0表示未损伤;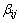 为单元损伤灵敏度因子,0<
为单元损伤灵敏度因子,0<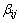 <1,
<1,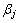 越大,则灵敏度越高;
越大,则灵敏度越高;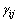 为单元损伤修正因子,是损伤位置和程度的函数,可以应用单元应变能求出。
为单元损伤修正因子,是损伤位置和程度的函数,可以应用单元应变能求出。
由式(28)可知:在结构的损伤程度一定的情况下(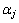 为定值),结构特征值变化率
为定值),结构特征值变化率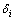 是应变能判别单元损伤灵敏度因子
是应变能判别单元损伤灵敏度因子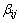 和单元损伤程度修正因子
和单元损伤程度修正因子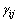 的函数。在模态和划分单元一定的情况下,
的函数。在模态和划分单元一定的情况下,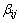 为定值,
为定值,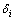 为
为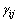 的函数,所以,
的函数,所以,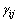 是结构损伤位置和程度判定的基本因子。式(28)就是基于特征值变化率和单元应变能的结构损伤识别的基本公式,应用式(28)可以对结构的损伤进行定位和程度识别。
是结构损伤位置和程度判定的基本因子。式(28)就是基于特征值变化率和单元应变能的结构损伤识别的基本公式,应用式(28)可以对结构的损伤进行定位和程度识别。
3 结构损伤识别方法和程序
3.1 模态的选择
根据损伤前后结构特征值变化率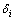 来选择用来进行结构损伤识别的模态,是用来判定模态对结构损伤灵敏度指标,变化率越大,说明本模态对结构损伤的损伤识别越灵敏。在一般情况下,取
来选择用来进行结构损伤识别的模态,是用来判定模态对结构损伤灵敏度指标,变化率越大,说明本模态对结构损伤的损伤识别越灵敏。在一般情况下,取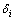 较大的模态,并且所选模态的
较大的模态,并且所选模态的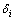 之间相差不能超过较大值的5%。本文采集结构损伤前后的各前10阶模态,取计算模态的标准为
之间相差不能超过较大值的5%。本文采集结构损伤前后的各前10阶模态,取计算模态的标准为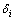 较大的模态为高效模态,取最灵敏度最高3~5阶进行计算。
较大的模态为高效模态,取最灵敏度最高3~5阶进行计算。
3.2 结构损伤位置判定
本过程应用单元损伤灵敏度因子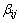 以及单元损伤程度修正因子
以及单元损伤程度修正因子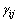 提出一个新的损伤定位指标
提出一个新的损伤定位指标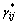 :
:
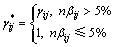 (29)
(29)
式中:n为结构的单元总数。
在一般情况下,在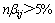 时具有较高的灵敏度。因为即使i阶模态下j单元发生损伤,但在
时具有较高的灵敏度。因为即使i阶模态下j单元发生损伤,但在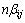 ≤5%时,也可能发生误判。为了避免误判发生,令在
≤5%时,也可能发生误判。为了避免误判发生,令在 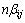 ≤5%的情况下,损伤定位指标
≤5%的情况下,损伤定位指标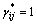 。
。
假设不同单元损伤定位指标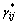 服从正态分布的变量,对
服从正态分布的变量,对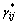 可以进行标准化处理:
可以进行标准化处理:
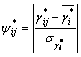 (30)
(30)
式中: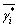 为i模态下个单元
为i模态下个单元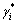 的平均值;
的平均值;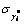 为方差。
为方差。
当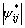 ≤2时,令
≤2时,令
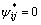 (31)
(31)
为了消除因为低应变能引起的测量噪音和数值计算误差对结构j单元损伤指标的误判,对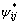 进行修正得:
进行修正得:
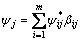 (32)
(32)
式中:m为最后采用的计算模态数。
由前面的推导可知,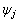 也服从正态分布,对其进行标准化处理得结构的损伤的判定指标
也服从正态分布,对其进行标准化处理得结构的损伤的判定指标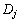 :
:
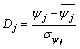 (33)
(33)
当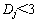 ,破损准则定义为:
,破损准则定义为: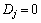 。
。
这样应用指标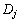 就能够判定结构的损伤单元,若单元的
就能够判定结构的损伤单元,若单元的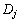 越大,其损伤的可能性就越大。
越大,其损伤的可能性就越大。
3.3 结构损伤程度识别
如果检测或计算了多个模态,式(28)就可以写成如下形式:
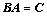 (34)
(34)
其中:
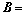
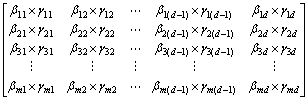
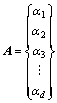 ,
,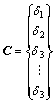 (35)
(35)
式中:m是采用计算的振动模态的阶数;d为总的损伤单元数。
当检测或数值计算的模态数大于损伤的单元数时(m≥d),应用最小二乘法进行拟合得结构的损伤程度可由下式进行计算:
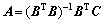 (36)
(36)
当检测的模态数小于损伤的单元数(m<d)时,可以应用扩展模态技术进行计算。在损伤程度识别过程中,本文结合小波降噪的方法降低特征值和模态振型的噪声影响,以便与实际工程检测处理方法结果保持一致。
3.4 结构损伤识别参数噪声处理
在实际结构的损伤识别过程中,检测过程中获得的模态数据要受到观测噪声的影响,本研究对检测的模态振型加入随机噪声[18-19],作为实测数据进行分析,随机噪声表达式如下:
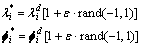 (37)
(37)
式中: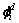 和
和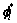 分别为结构加噪前后第i阶模态振型,
分别为结构加噪前后第i阶模态振型,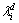 和
和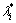 分别代表结构加噪前后的特征值;
分别代表结构加噪前后的特征值;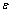 为加噪水平;
为加噪水平;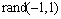 为在[-1, 1]内的随机正态分布变量。
为在[-1, 1]内的随机正态分布变量。
实测数据的处理过程中往往需要降噪,本文在损伤位置识别的过程中应用式(30),(32)和(33)来降低噪声的影响,在损伤程度识别时采用小波降噪的方法来提高识别精度。
4 实例验证
4.1 工程概况及有限元建模
双圆筒式结构是一种新型防浪堤结构型式,其结构由钢筋混凝土浇筑而成。2个圆筒之间由隔板连接,2个圆形截面组合成的空间薄壳结构作为挡浪结构。圆筒的内径为10 m,壁厚为0.35 m,隔板厚度为0.6 m。其结构尺寸和三维模型见图1。双圆筒结构的薄壁由于施工或使用可能局部产生损伤,由于结构的工作环境在海水中,因此,这种损伤对结构的危害很大,应及早发现并采取维护措施来避免较大的工程事故。根据结构的受力特征,采用有限元分析软件ANSYS建立了双圆筒壳体结构的有限元模型,并且在上部结构和基础接触处采用固结方式连接,上部结构采用壳体单元(SHELL63,图2),共计520个单元。
根据本文方法采用Matlab编制计算程序,以新型双圆筒防浪堤的上部壳体结构为例,对结构的一处损伤和多处损伤在不同噪声情况下进行损伤识别。
4.2 单一位置损伤的识别
利用单元刚度的降低来模拟单元的损伤,有限元计算中通过对弹性模量的改变来模拟结构的损伤。假定结构的199号单元发生不同程度的损伤(如图2所示),采用本文方法对结构的损伤进行识别。损伤程度降低量分别为5%,10%,15%,20%,30%,40%,50%和60%。
4.2.1 模态的选择
通过有限元计算提取了结构损伤前后的前10阶模态。不同损伤程度下壳体结构的特征值在损伤前后的变化率计算结果见图3所示。从图3可以看出:壳体结构的1,5,6阶模态变化率较大。因此,选用1,5和6阶模态进行损伤识别计算。
4.2.2 损伤位置的识别
应用结构损伤判别指标D作为结构损伤定位的标识量,提取1,5和6阶模态的振型,根据工程的实际受损情况进行模拟。结构发生40%损伤时无噪声、加入5%噪声和加入10%噪声共3种情况下损伤结果分别如图4~6所示。从图4~6可以看出:损伤单元的D比非损伤单元的D要大得多,这样,根据计算的D就能判定发生损伤的单元。D的较大差异也说明应用本文所提的方法能够较好地识别出结构的损伤位置。
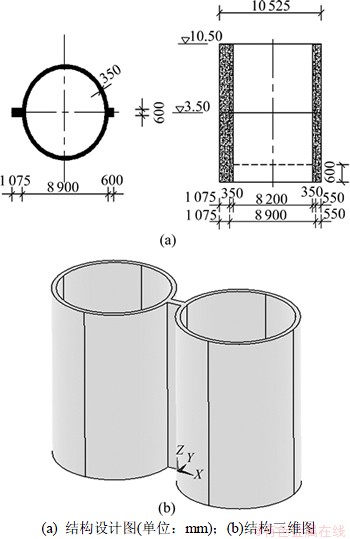
图1 双圆筒式结构图
Fig.1 Double-cylinder structure
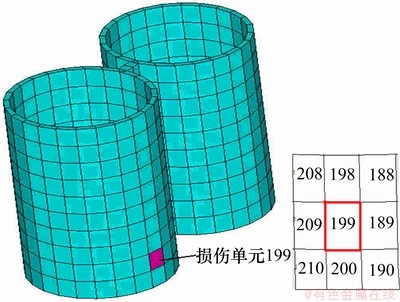
图2 结构单一位置损伤
Fig.2 A single location damage of structure
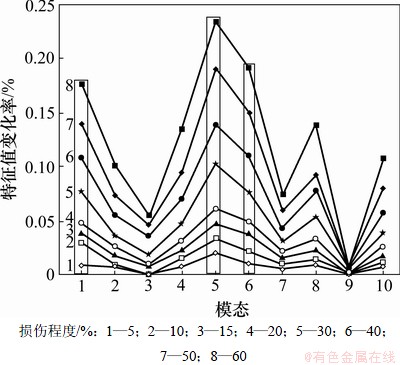
图3 单位置损伤识别模态的选取
Fig.3 Modal selection for single location damage identification
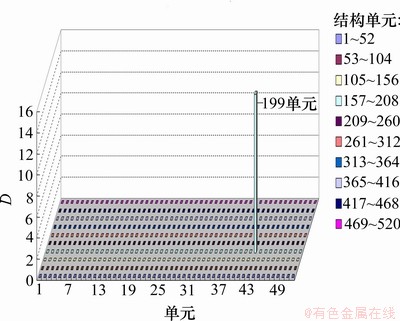
图4 没有噪声的情况下单一位置损伤识别结果
Fig.4 Damage identification results for a single position damage without noise
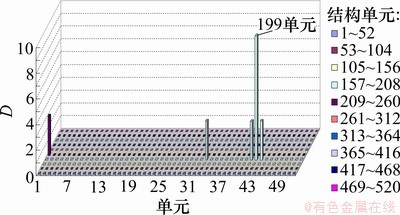
图5 5%噪声情况下单一位置损伤识别结果
Fig.5 Damage identification results for a single position damage with 5% noise
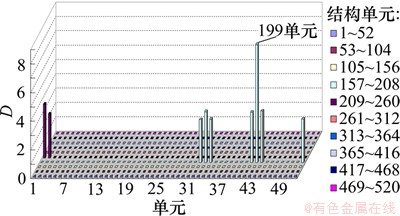
图6 10%噪声情况下单一位置损伤识别结果
Fig.6 Damage identification results for a single position damage with 10% noise
图7所示为199号单元在受损伤程度分别为5%,10%,15%,20%,30%,40%,50%和60%时在无噪声、5%噪声、10%噪声影响3种情况下的D变化情况。从图7可知:噪声一定的情况下,D随着损伤程度的增大而增大。在损伤程度一定的情况下,在检测过程中,噪声越小,对应的D越大。
4.2.3 损伤程度的识别
根据式(36)对不同损伤和不同噪声情况下壳体结构的损伤程度进行识别计算,计算结果见表1。从表1可见:在无噪声、5%噪声和10%噪声情况下,结构损伤程度识别的误差分别为3%以内,5%以内和10%以内,说明噪声对结构损伤程度影响较大,但在单一损伤情况下,本文提出的识别方法在10%的噪声内结构损伤不同程度的识别均具有较高的精度。
4.3 多处位置损伤的识别
与单一位置损伤计算方法一样,假定结构的193单元、199单元和315单元发生不同程度的损伤(如图8所示),采用本文的方法对结构的损伤进行识别。
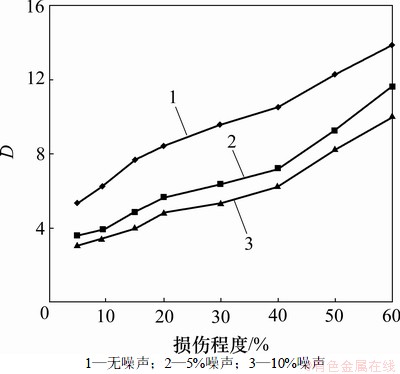
图7 199单元不同噪声下不同损伤程度的D
Fig.7 DI of different degrees of damage with different noise for element No.199
4.3.1 模态选择
在损伤程度分别为5%,10%,15%,20%,30%,40%,50%和60%的情况下通过有限元计算提取结构损伤前、后的前10阶模态,不同损伤程度下壳体结构的特征值在损伤前后的变化率计算结果见图9。从图9可以看出:壳体结构的1,5,6和8阶模态变化率较大,所以,选用1,5,6和8阶模态进行损伤识别计算。
4.3.2 损伤位置的识别
提取1,5,6和8阶模态的振型,根据工程的实际受损情况进行模拟。在单元193发生30%损伤、单元199发生40%损伤、单元315发生50%损伤的工况下,无噪声、加入5%噪声和加入10%噪声情况下损伤位置识别结果分别如图10~12所示。从图10可以看出:单元193、单元199和单元315的D很大,其他单元的D为0,说明在无噪声情况下能够很精确地识别出结构的损伤位置。由图11和图12可知,在5%和10%噪声干扰下,和损伤单元相邻并有共同节点的单元的D不在为0,但与损伤单元的D相比,损伤单元的D比非损伤单元的D要大得多。D差异较大也说明了应用本文所提的方法能够较好地识别出结构的损伤位置。在较高噪声下,能够精确识别损伤单元的位置,说明本文的计算方法对多处损伤结构的损伤位置识别具有很好的鲁棒性。
表1 损伤单元199的损伤程度计算结果
Table 1 Calculation results of damage degree for element No.199 with different noises
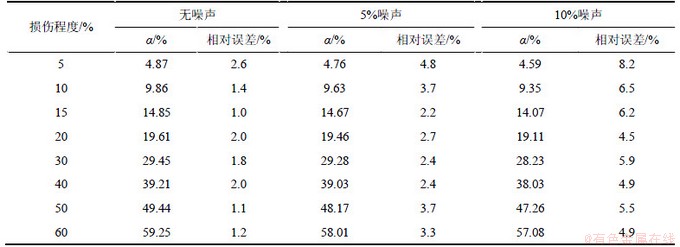
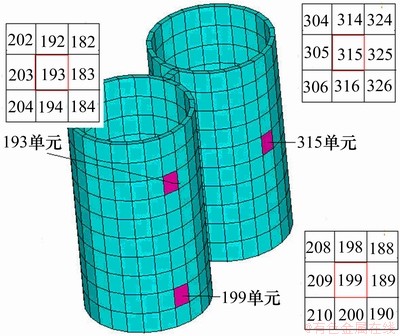
图8 结构多位置损伤
Fig.8 Multiple damage of structure
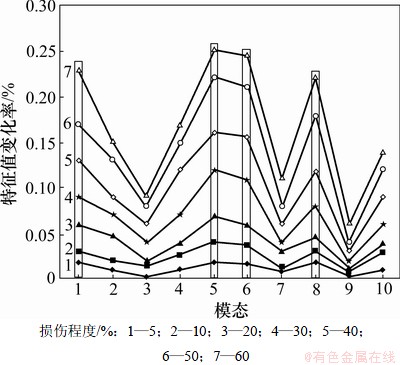
图9 结构多损伤情况下模态的选取
Fig.9 Modal selection for multi-position damage identification
4.3.3 损伤程度的识别
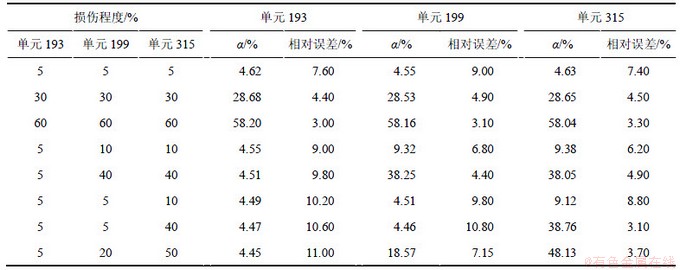
根据式(36)对不同损伤和不同噪声情况下壳体结构的损伤程度进行识别计算,计算结果见表2~4。从表2~4可知:在多种损伤的情况下,损伤的程度相差越大,较小的损伤处的识别误差越大;当多处的损伤程度相近时,各个位置损伤识别都有较高的识别精度。即使多处都是较小的损伤,损伤程度识别误差也较小,说明本方法对相差不大的损伤程度的识别具有较高的精度。若损伤程度相差较大,则较小的损伤单元识别误差较大。从表2~4还可以看出:在同样的工况下,噪声越大,损伤程度识别的误差也越大,但是,识别相对误差基本上在10%之内,说明本方法对结构的损伤程度识别具有较好的鲁棒性。
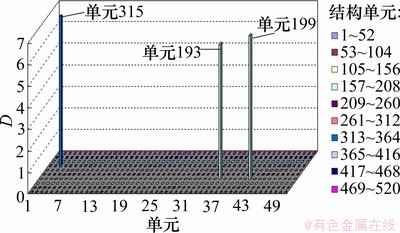
图10 没有噪声的情况下多位置损伤识别结果
Fig.10 Damage identification results for multi-position damage without noise
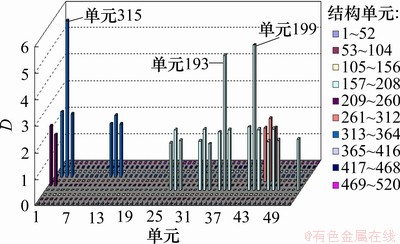
图11 5%噪声的情况下多位置损伤识别结果
Fig.11 Damage identification results for multi-position damage with 5% noise
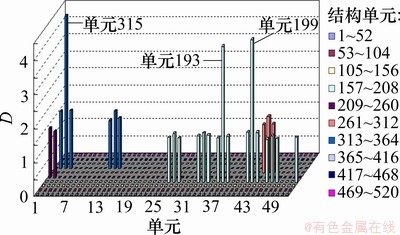
图12 10%噪声的情况下多位置损伤识别结果
Fig.12 Damage identification results for multi-position damage with 10% noise
表2 无噪声下多处损伤时的损伤程度计算结果
Table 2 Severity of damage calculation results for multi-position damage without noise
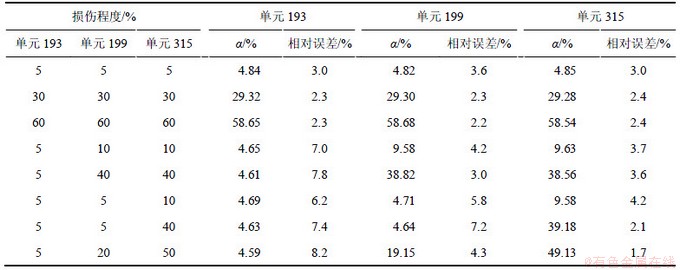
表3 5%噪声下多处损伤时的损伤程度计算结果
Table 3 Severity of damage calculation results for multi-position damage with 5% noise
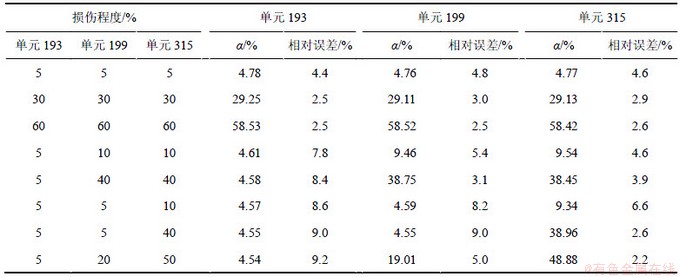
表4 10%噪声下多处损伤时的损伤程度计算结果
Table 4 Severity of damage calculation results for multi-position damage with 10% noise
5 结论
(1) 本文提出的结构的损伤识别方法应用结构的固有频率变化率选择对损伤灵敏度较高的高效模态识别结构的损伤程度,能够准确地对三维结构的单一损伤和多处损伤损伤位置和程度进行识别。
(2) 本文提出的损伤识别方法在不同噪声干扰下能够较精确地识别出损伤的位置和程度,说明本方法具有较好的鲁棒性。
(3) 本文提出的方法仅需要知道损伤前、后的几个低阶的模态振型和模态特征值,在工程应用中具有实用价值。
参考文献:
[1] 朱宏平, 余璟, 张俊兵. 结构损伤动力检测与健康监测研究现状与展望[J]. 工程力学, 2012, 28(2): 1-11.
ZHU Hongping, YU Jing, ZHANG Junbing. A summary review and advantages of vibration-based damage identification methods in structural health monitoring[J]. Engineering Mechanics, 2012, 28(2): 1-11.
[2] Lifshitz J M, Rotem A. Determination of reinforcement unbonding of composites by a vibration technique[J]. Journal of Composite Materials, 1969(3): 412-423.
[3] Salawu O S. Detection of structural damage through changes in frequency: A review[J]. Engineering Structures, 1997, 19(9): 718-723.
[4] 郑栋梁, 李中付, 华宏星. 结构早期损伤识别技术的现状和发展趋势[J]. 振动与冲击, 2002, 21(2): 1-6.
ZHENG Dongliang, LI Zhongfu, HUA Hongxing. A summary review of structural initial damage identification methods[J]. Journal of Vibration and Shock, 2002, 21(2): 1-6.
[5] Kim J T, Ryu Y S, Cho H M, et al. Damage identification in beam-type structures: Frequency-based method vs mode-shape- based method[J]. Engineering Structures, 2003, 25(1): 57-67.
[6] Kim J T, Park J H, Lee B J. Vibration-based damage monitoring in model plategirder bridges under uncertain temperature conditions[J]. Engineering Structures, 2007, 29(7): 1354-1365.
[7] Tomaszewska A. Influence of statistical errors on damage detection based on structural flexibility and mode shape curvature[J]. Computers and Structures, 2010, 88(3): 154-164.
[8] Shi Z Y, Law S S, Zhang L M. Structural damage localization from modal strain energy change[J]. Journal of Sound and Vibration, 1998, 218(5): 825-844.
[9] Shi Z Y, Law S S, Zhang L M. Improved damage quantification from elemental modal strain energy change[J]. Journal of Engineering Mechanics-Asce, 2002, 128(5): 521-529.
[10] 王学广, 贺国京. 高精度模态应变能法结构损伤检测研究[J]. 铁道学报, 2005, 27(5): 92-95.
WANG Xueguang, HE Guojing. Effective structural damage detection method based on modal strain energy[J]. Journal of the China Railway Society, 2005, 27(5): 92-95.
[11] 颜王吉, 黄天立, 任伟新, 等. 基于单元模态应变能灵敏度的结构损伤统计识别[J]. 中南大学学报: 自然科学版, 2011, 42(1): 152-157.
YAN Wangji, HUANG Tangli, REN Weixin, et al. Statistical damage identification of structures based on element modal strain energy sensitivity[J]. Journal of Central South University: Science and Technology, 2011, 42(1): 152-157.
[12] Hadjileontiadis L J, Douka E, Trochidis A. Fractal dimension analysis for crack identification in beam structures[J]. Mechanical Systems and Signal Processing, 2005, 19(3): 659-674.
[13] WEI Fan, PI Zhongqiao. A strain energy-based damage severity correction factor method for damage identification in plate-type structures[J]. Mechanical Systems and Signal Processing, 2012(28): 660-678.
[14] 赵玲, 李爱群. 基于单元应变能变化率的结构损伤识别方法[J]. 东南大学学报: 自然科学版, 2007, 37(6): 1052-1056.
ZHAO Ling, LI Aiqun. Structural damage identification method based on elemental strain energy change ratio[J]. Journal of Southeast University: Natural Science Edition, 2007, 37(6): 1052-1056.
[15] YANG Hezhen, LI Huajun, WANG Shuqing. Damage localization of offshore platform under ambient excitation[J]. China Ocean Engineering, 2003, 17(4): 307-316.
[16] LI Huajun, FANG Hui, HU S L J. Damage localization and severity estimate for three dimensional frame structures[J]. Journal of Sound and Vibration, 2007, 301(3): 481-494.
[17] HU Huiwen, WU Chengbo, LU Weijun. Damage detection of circular hollow cylinder using modal strain energy and scanning damage index methods[J]. Computers and Structures, 2011, 89(1): 149-160.
[18] Kim H M, Bartkowicz T J. Damage detection and health monitoring of large space structure[J]. Journal of Sound and Vibration, 1993, 27(6): 12-17.
[19] 张纯, 宋固全. 去噪正则化模型修正方法在桥梁损伤识别中的应用[J]. 振动工程学报, 2012, 25(1): 97-102.
ZHANG Chun, SONG Guquan. Bridge damage identification by finite element model updatingwith Tikhonov regularization and wavelet denoising[J]. Journal of Vibration Engineering, 2012, 25(1): 97-102.
(编辑 赵俊)
收稿日期:2012-07-18;修回日期:2012-10-15
基金项目:国家自然科学基金面上项目(11072143);浙江省教育厅科研项目(Y201223039)
通信作者:姚文娟(1957-),女,江西南昌人,博士,教授,从事结构分析及工程损伤等研究;电话:021-56336721;E-mail: wjyao@shu.edu.cn