高速移动荷载作用下板式轨道混凝土应变速率研究
徐浩,王平,王彪,赵坪锐
(西南交通大学 高速铁路线路工程教育部重点实验室,四川 成都,610031)
摘要:基于有限元理论,运用ANSYS软件,建立路基及桥上板式无砟轨道的动力有限元模型,计算不同荷载工况下板式轨道的混凝土应变速率。结果表明:随着列车速度的提高,板式轨道混凝土应变速率逐渐增大。路基上板式轨道的混凝土应变速率较桥梁上的板式轨道混凝土应变速率大。多个移动荷载作用下板式轨道混凝土应变速率较单个移动荷载大,板式轨道混凝土应变速率在10-4~10-2 s-1处于动态性能范畴。
关键词:板式轨道;混凝土;应变速率;移动荷载;动态性能
中图分类号:U213.2 文献标志码:A 文章编号:1672-7207(2014)06-2092-07
Concrete strain rate of slab track under high speed moving load
XU Hao, WANG Ping, WANG Biao, ZHAO Pingrui
(Key Laboratory of High-speed Railway Engineering, Ministry of Education,
Southwest Jiaotong University, Chengdu 610031, China)
Abstract: The dynamic finite element model of slab track on the subgrade or bridge was established based on the theory of finite element and ANSYS software to calculate the concrete strain rate of slab track in different load cases. The results indicate that the concrete strain rate of slab track increases with the improvement of train speed and it is bigger than the slab track on the bridge. The concrete strain rate of slab track under multiple moving loads is larger than that under single moving load. The concrete strain rate of slab track is from 10-4 to 10-2 s-1, and the strain rate is in dynamic performance category of concrete.
Key words: slab track; concrete; strain rate; moving load; dynamic property
单元板式无砟轨道以其高稳定性、高平顺性、少维修等优点在我国高速铁路上作为一种主要的轨道结构型式得到了广泛应用[1]。板式无砟轨道承受着高速列车的反复动荷载作用,国内外学者对板式无砟轨道的动力性能进行了大量研究[2-4],还有学者专门针对不同型式的板式轨道,对比分析了框架型板式轨道和平板型板式轨道的动力响应[5],因此对板式轨道的动力特性有了一定了解。
板式无砟轨道是一种钢筋混凝土组合结构,而混凝土材料是率敏感材料[6],因此板式无砟轨道在高速列车荷载作用下必然也存在应变速率敏感性。大量的研究表明:混凝土随着应变速率的不同,其力学性能如强度、延性、弹性模量等力学参数均不相同[7-9],同时形成了不同的动力本构模型与基础理论[10]。尽管对于混凝土的率敏感性进行了大量的理论和试验研究,却未发现有将混凝土应变速率的相关研究成果应用于板式轨道动力分析的文献。在混凝土结构设计中,必须考虑混凝土在动态作用下所表现出的与准静态作用完全不同的力学性能,这已经得到国内外广大研究者的共识,本文作者拟采用文献[11]中的方法,建立高速移动荷载作用下板式无砟轨道动力有限元模型,计算路基及桥上板式无砟轨道的混凝土应变速率,从而从板式轨道混凝土应变速率方面了解板式轨道的动力特性。
1 板式轨道动力有限元模型
1.1 数值分析模型及计算参数
板式无砟轨道由钢轨、扣件系统、预制混凝土轨道板、水泥乳化沥青砂浆层(CA砂浆)和混凝土底座(支承层)等部分组成,板式轨道在路基及桥梁上的计算模型如图1所示。
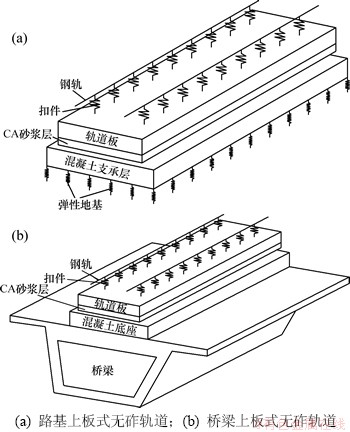
图1 板式无砟轨道计算模型
Fig. 1 Computation model of slab track
为了消除边界条件对轨道系统受力状态的影响,在路基上由于一块支承层的长度等效为4块轨道板的长度,因此路基上选取4块轨道板进行模拟,由于简支梁桥的长度约等效为6块轨道的长度,因此桥梁上选取6块轨道板进行模拟,以中间1块轨道板作为主要分析对象,由于路基及桥梁是整个轨道的基础,因此模型中也考虑弹性地基与桥梁。
钢轨直接承受列车传来的压力、冲击与振动,模型中将其看成无限长的点支承梁,采用能模拟铁摩辛柯梁的单元BEAM188模拟,钢轨采用60 kg/m标准钢轨,轨距为1.435 m,钢轨支点间距取为0.629 m。钢轨与轨道板之间的扣件和轨下胶垫等联结件,忽略其非线性因素,等效为一个线性弹性件,采用弹簧阻尼单元COMBIN14模拟,扣件的动刚度取为50 kN/mm。预制轨道板是板式轨道的主要承重构件,混凝土强度等级为C60,标准轨道板宽度为2.4 m,长度为4.962 m,厚度为0.19 m。水泥乳化沥青砂浆层的厚度为50 mm,弹性模量为300 MPa,路基地段混凝土支承层采用强度等级为C40的混凝土,长度为4块轨道板的长度,底座缝与轨道板板缝对齐,混凝土支承层宽3.0 m,厚度为0.3 m,而桥梁上混凝土底座的长度与轨道板等长,为4.962 m,宽度为2.8 m,厚度为0.2 mm,底座板混凝土强度等级仍为C40。路基的地基系数根据文献[1,12-13]取为75 MPa/m,为了计算方便路基层采用等效的线弹性单元COMBIN14模拟,其刚度根据路基系数进行计算。桥梁结构按32 m简支梁桥标准截面考虑,桥梁的混凝土强度等级为C60。由于预制轨道板、CA砂浆、混凝土支承层及桥梁结构的基本形状比较规则,所以在建立三维有限元模型时,采用空间八节点六面体单元SOLID45模拟。为了简化分析,轨道板及以下各层通过共用节点连接,钢轨与轨道板间通过弹簧阻尼单元连接,对于桥梁上板式轨道,混凝土底座与桥梁间也采用共用节点连接。
在有限元分析中,由于网格尺寸对计算结果有一定的影响,本文作者参考文献[1],将每个钢轨支点范围内沿线路方向划分为4个单元,每个单元的长边和短边之比小于1.5,保证了计算精度的合理性。
1.2 荷载模型
作用在板式轨道上的移动荷载通常可以根据轨道参数及不平顺值、机车类型和列车速度等计算出来,也可以通过实测得到[14],还可以利用列车-轨道系统动力分析模型计算得到,而最常见、最简单的方法是将轮轨动力简化成一系列轴载[15],并直接施加在钢轨上,分析中忽略轨道不平顺的影响。
为了分析不同荷载形式对板式轨道混凝土应变速率的影响,本文拟定了5种荷载工况,分别如下。
工况1:单个移动荷载,荷载为定值,采用单轴双轮300 kN。
工况2:单个移动荷载,荷载为采用列车-轨道系统动力分析计算得到的值,荷载沿轨道结构纵向为变化荷载。
工况3:多个移动荷载,模拟一节动车共4个对轮对,荷载为定值,采用单轴双轮300 kN。
工况4:多个移动荷载,模拟一节动车共4个轮对,荷载为采用列车-轨道系统动力分析计算得到,荷载沿轨道结构纵向为变化荷载,假定4个轮对的轮轨相互作用力时程曲线一致。
工况5:单个定值移动荷载以不同速度行驶于路基上板式轨道,荷载采用单轴双轮300 kN(速度从200 km/h增大到350 km/h,增幅为50 km/h)。
单个移动荷载直接布置在模型的左端,而多个移动荷载模拟一节动车的4个轮对,其中模拟第1个轮对的荷载布置在模型的左端,模拟其他3个轮对的移动荷载按实际轮对的距离依次布置,移动荷载均从模型左端以不同的速度移动至模型的右端。
单个变值移动荷载与多个变值移动荷载的时间历程曲线如图2所示。
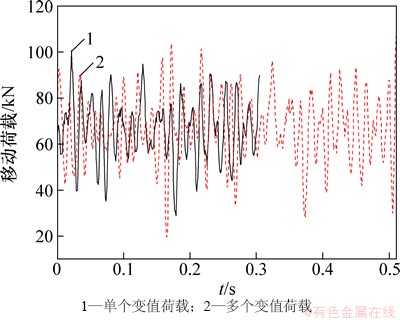
图2 移动荷载时程曲线
Fig. 2 Time history curve of moving load
1.3 边界条件
为减小边界条件的影响,钢轨两端采用全约束,模型两端约束其纵横向位移,对于路基上板式轨道路基弹簧采用全约束,而桥梁上板式轨道的桥梁结构一端为固定支座,考虑到桥梁固定支座具有一定的纵向刚度,因此固定支座端采用约束其垂向位移,同时利用弹簧阻尼单元模拟固定支座处的纵向刚度,对于桥梁结构的活动支座端则仅约束其垂向位移。
2 板式轨道混凝土应变率计算方法
首先利用ANSYS有限元软件分析不同工况下轨道板、底座板以及桥梁结构的垂向压应力时程曲线,假定某一时间t下轨道板、混凝土底座及桥梁的垂向压应力为σ(t),则不同时间下轨道板、混凝土底座及桥梁的垂向应变为:
ε(t)=σ(t)/E (1)
式中:E为轨道板、混凝土底座及简支梁桥等的弹性模量,根据垂向应变的时程变化曲线,对其进行一阶求导,即得到板式轨道系统各部分的混凝土垂向应变速率。
ε'(t)=dε(t)/dt=dσ(t)/Edt (2)
式中:ε'(t)为板式轨道的混凝土的垂向应变速率。
3 数值模拟结果及分析
本文着重探讨路基及桥上板式无砟轨道的各结构层的混凝土应变速率。
3.1 单个定值移动荷载
对于路基上选取模型中第2块轨道板、桥梁上选取模型中第3块轨道板上第4个扣件处对应的位置分析轨道板和底座板(支承层)的应力变化情况,为了表述方便,下文分析时选取点的应力时程曲线采用“同一位置”表达。图3所示为单个定值移动荷载以350 km/h的速度驶过板式轨道时轨道板、底座板(支承层)的垂向压应力时程曲线(负号表示所受的垂向应力为压应力)。
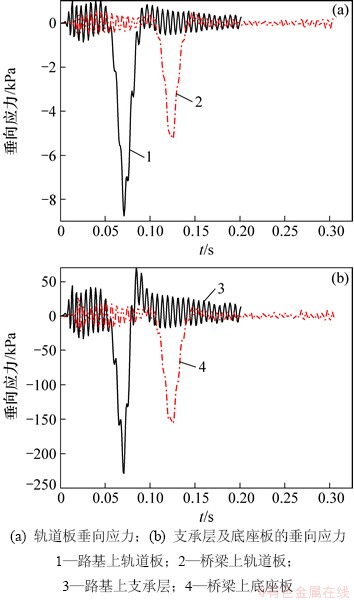
图3 单个定值移动荷载下板式轨道垂向应力时程曲线
Fig. 3 Vertical stress time history curve of slab track under a single constant moving load
从图3可知:在单个定值移动荷载作用下,路基上板式无砟轨道的轨道板最大垂向压应力为8.747 MPa,支承层的最大垂向压应力为228.61 kPa,而桥梁上板式轨道的轨道板和底座板的垂向最大压应力分别为5.237和155.89 kPa。单个定值移动荷载作用下,路基上板式轨道的轨道板、支承层的垂向压应力均大于桥梁上板式无砟轨道的轨道板和底座板,这是由于桥梁上板式无砟轨道的整体刚度较路基大,因此轨道板、底座板的垂向变形较小,从而导致桥梁上板式轨道轨道板和底座板的最大垂向压应力均较路基的小。
对于路基及桥上板式无砟轨道,采用式(2)得到单个定值移动荷载以350 km/h的速度驶过时,轨道板、底座板(支承层)的混凝土垂向应变率如图4所示。从图4可知:在单个定值移动荷载作用下,路基上板式轨道轨道板的混凝土最大应变速率为4.19×10-2 s-1,支承层的混凝土最大应变速率为1.713×10-3 s-1,桥梁上板式轨道轨道板的混凝土最大应变速率为2.15×10-2 s-1,底座板的混凝土最大应变速率为1.12×10-3 s-1,可见路基上板式轨道的混凝土最大应变速率均大于桥梁上板式无砟轨道。
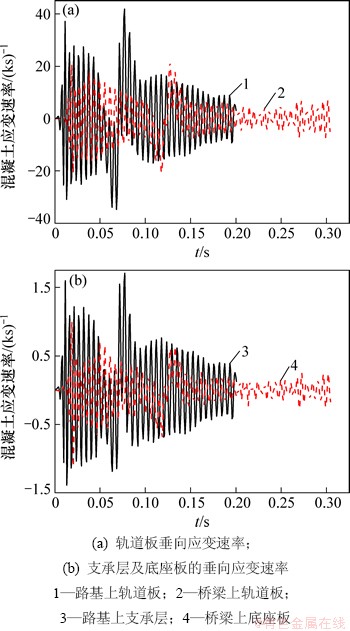
图4 单个定值移动荷载下板式轨道混凝土应变速率
Fig. 4 Concrete strain rate of slab track under a single constant moving load
3.2 单个变值移动荷载
采用上述计算方法,路基及桥梁上板式轨道在单个变值移动荷载作用下,同一位置处轨道板、底座板(支承层)的混凝土应变速率如图5所示。
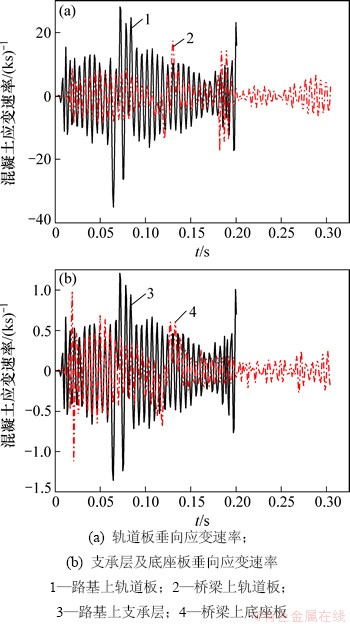
图5 板式轨道混凝土应变速率
Fig. 5 Concrete strain rate of slab track
由图5可知:在单个变值移动荷载作用下,路基上板式轨道轨道板的混凝土最大应变速率为3.5×10-2 s-1,支承层的混凝土最大应变速率为1.36×10-3 s-1,桥梁上板式轨道轨道板的混凝土最大应变速率为1.74×10-2 s-1,底座板的混凝土最大应变速率为1.12×10-3 s-1,在单个变值移动荷载作用下,路基上板式轨道的混凝土最大应变速率均大于桥梁上板式无砟轨道。
由图4和图5还可以看出:在单个定值移动荷载作用下板式轨道的混凝土最大应变速率较通过列车-轨道系统动力学计算出来的单个变值移动荷载的大,这是由于单个定值移动荷载幅值较变值大,作用在轨道结构上的冲击作用大,因此板式轨道的混凝土应变速率增大。
3.3 多个定值移动荷载
图6所示为多个定值移动荷载以350 km/h的速度驶过板式轨道时,同一位置处轨道板、底座板(支承层)的垂向压应力时程曲线。
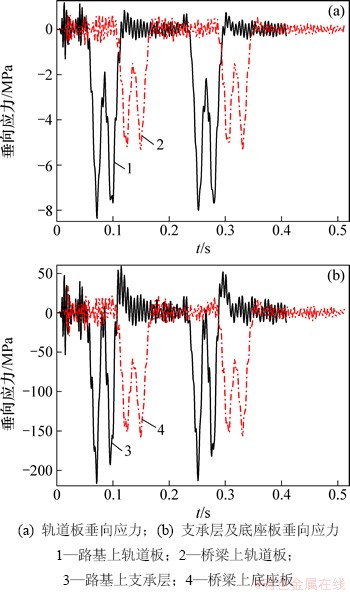
图6 多个定值移动荷载下板式轨道垂向应力时程曲线
Fig. 6 Vertical stress time history curve of slab track under mutiple constant moving load
在多个定值移动荷载作用下,路基上板式无砟轨道的轨道板垂向压应力最大值为8.354 MPa,支承层的最大垂向压应力为216.69 kPa,而桥梁上板式轨道的轨道板和底座板的垂向最大压应力分别为5.392 MPa和159.52 kPa。在多个定值移动荷载作用下,由于桥梁上板式无砟轨道的整体刚度较路基大,轨道板、底座板的垂向变形较小,因此路基上板式轨道的轨道板、支承层的垂向压应力依然均大于桥梁上板式无砟轨道。
在多个定值移动荷载作用下,路基及桥梁上板式轨道的轨道板、底座板(支承层)混凝土应变速率如图7所示。由图7可知:在多个定值移动荷载作用下,路基上板式轨道轨道板的混凝土最大应变速率为5.31×10-2 s-1,支承层的混凝土最大应变速率为2.295×10-3 s-1,桥梁上板式轨道轨道板的混凝土最大应变速率为3.302×10-2 s-1,底座板的混凝土最大应变速率为1.545×10-3 s-1,在多个定值移动荷载作用下,路基上板式轨道的轨道板、底座板的混凝土最大应变速率依然大于桥梁上板式无砟轨道。
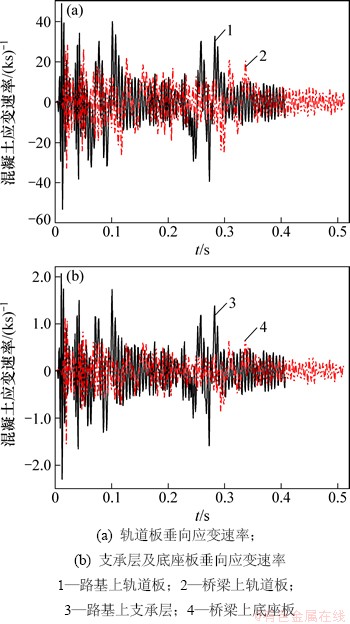
图7 多个定值移动荷载下板式轨道混凝土应变速率
Fig. 7 Concrete strain rate of slab track under mutiple constant moving load
3.4 多个变值移动荷载
采用上述计算方法,路基及桥梁上板式轨道在多个变值移动荷载作用下,同一位置处轨道板、底座板(支承层)的混凝土应变速率如图8所示。由图8可知:在多个变值移动荷载作用下,路基上板式轨道轨道板的混凝土最大应变速率为4.43×10-2 s-1,支承层的混凝土最大应变速率为1.92×10-3 s-1,桥梁上板式轨道轨道板的混凝土最大应变速率为4.056×10-2 s-1,底座板的混凝土最大应变速率为1.44×10-3 s-1,在多个变值移动荷载作用下,路基上板式轨道的混凝土最大应变速率也大于桥梁上板式无砟轨道。
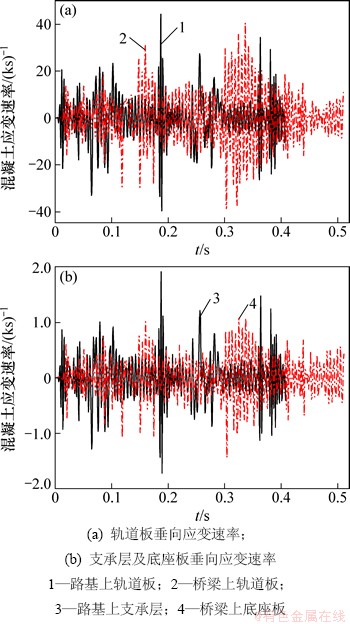
图8 多个变值移动荷载下板式轨道混凝土应变速率
Fig. 8 Concrete strain rate of slab track under multiple variable moving load
单个移动荷载与多个移动荷载作用下板式轨道混凝土最大应变速率对比如表1所示。
从单个移动荷载与多个移动荷载作用下板式轨道混凝土最大应变率对比可知,多个移动荷载作用下板式轨道的混凝土最大应变速率大于单个移动荷载的作用,由于多个移动荷载共同作用时荷载之间会产生相互作用,从而使板式轨道的混凝土应变速率较大。
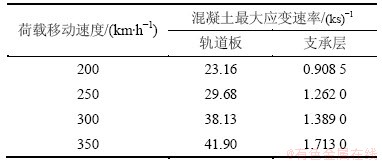
3.5 不同速度下单个定值移动荷载
当单个定值移动荷载以不同速度通过路基上板式轨道时,不同列车速度下板式轨道混凝土最大应变速率如表2所示。从表2可知:随着列车速度的提高,板式轨道混凝土最大应变速率不断增大,这是由于随着列车速度的增大,作用在轨道结构上的荷载冲击作用不断加大,引起板式轨道的轨道板、支承层垂向应变变化加剧,从而导致列车速度增大,板式轨道混凝土最大应变速率增大。
表1 不同荷载工况下板式轨道混凝土最大应变速率
Table 1 Maximum concrete strain rate of slab track under different kinds of loads 应变速率/(ks)-1
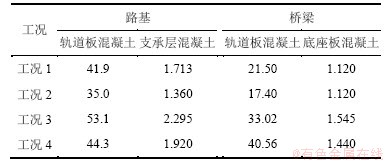
表2 不同速度下板式轨道混凝土最大应变速率
Table 2 Maximum concrete strain rate of slab track under different kinds of speeds
综上所述,路基上板式轨道的混凝土应变速率均大于桥梁上板式轨道的混凝土应变速率,且板式轨道的轨道板、底座板(支承层)的混凝土应变速率处于10-4~10-2 s-1范围内,说明板式轨道混凝土处于动态特性的范畴 [16],因此建议板式轨道的设计与检算应将混凝土动态性能引入,从而使板式轨道的设计理论更加完善。
4 结论
(1) 随着移动荷载速度的提高,板式轨道的混凝土的最大应变速率不断增大。
(2) 由于桥梁上板式轨道的整体刚度较大,路基上板式轨道的混凝土最大应变速率较桥梁上板式轨道的混凝土最大应变速率大。
(3) 通过列车-轨道系统动力学计算出的变值移动荷载作用下板式轨道的混凝土最大应变速率较定值移动荷载的小,这是由于变值移动荷载冲击作用较小,其产生的垂向应力相对较小所致。
(4) 尽管多个移动荷载作用下板式轨道的垂向应力较单个移动荷载的小,但其混凝土的最大应变速率明显增大,建议进行板式轨道的混凝土应变速率计算时应考虑多轮对共同作用的影响。
(5) 板式轨道的混凝土应变速率的变化范围为10-4~10-2 s-1,处于混凝土动态特性的范畴,因此建议板式轨道的设计与检算应考虑混凝土的动态性能,从而为板式轨道设计理论的完善提供一定的理论依据。
参考文献:
[1] 刘学毅, 赵坪锐, 杨荣山, 等. 客运专线无砟轨道设计理论与方法[M]. 成都: 西南交通大学出版社, 2010: 1-10.
LIU Xueyi, ZHAO Pingrui, YANG Rongshan, et al. Research on the design theory and method for ballastless track on passenger dedicated line[M]. Chengdu: Southwest Jiaotong University Press, 2010: 1-10.
[2] 蔡成标, 翟婉明, 王开云. 高速列车与桥上板式轨道动力学仿真分析[J]. 中国铁道科学, 2004, 25(5): 57-60.
CAI Chengbiao, ZHAI Wanming, WANG Kaiyun. Dynamics simulation of interactions between high-speed train and slab track laid on bridge[J]. China Railway Science, 2004, 25(5): 57-60.
[3] 向俊, 曹晔, 刘保钢, 等. 客运专线板式无碴轨道动力设计参数[J]. 中南大学学报(自然科学版), 2007, 38(5): 981-986.
XIANG Jun, CAO Ye, LIU Baogang, et al. Dynamic parameters of slab track of passenger transport line[J]. Journal of Central South University (Science and Technology), 2007, 38(5): 981-986.
[4] Esveld, C. Modern Railway Track 2nd Edition[M]. Zaltbommel: MRT Productions, 2001.
[5] 蔡成标, 徐鹏. 高速铁路框架型板式轨道动力学分析[J]. 振动工程学报, 2011, 24(2): 164-169.
CAI Chengbiao, XU Peng. Dynamic analysis for frame slab track of high-speed railway[J]. Journal of Vibration Engineering, 2011, 24(2): 164-169.
[6] Abrams D A. Effect of rate of application of load on the compressive strength of concrete[J]. ASTM Journal, 1917, 17: 364-377.
[7] 刘鹏. 混凝土动态力学性能试验研究与数值分析[D]. 大连: 大连大学建筑工程学院, 2011: 2-56.
LIU Peng. Experimental research and numerical analysis on dynamic mechanical properties of concrete[D]. Dalian: Dalian University. College of Civil Engineering and Architecture, 2011: 2-56.
[8] 刘鹏, 关萍, 王怀亮. 应变率对混凝土动态强度性能影响的研究进展[J]. 大连大学学报, 2009(6): 79-84.
LIU Peng, GUAN Ping, WANG Huailiang. Research progress of strain rate on dynamic strength properties of concrete[J]. Journal of Dalian University, 2009(6): 79-84.
[9] 肖诗云, 张剑. 不同应变率下混凝土受压损伤试验研究[J]. 土木工程学报, 2010, 43(3): 40-45.
XIAO Shiyun, ZHANG Jian. Compressive damage experiment of concrete at different strain rates[J]. China Civil Engineering Journal, 2010, 43(3): 40-45.
[10] 杜荣强, 林皋, 冷飞. 混凝土动力本构模型的基础理论与建模应用综述[J]. 世界地震工程, 2007, 23(2): 5-11.
DU Rongqiang, LIN Gao, LENG Fei. A summary of fundamentals and applications for dynamic constitutive modelling of concrete[J]. World Earthquake Engineering, 2007, 23(2): 5-11.
[11] 宋小林, 翟婉明. 高速移动荷载作用下CRTSⅡ型板式无砟轨道基础结构应力分布规律[J]. 中国铁道科学, 2012, 33(4): 1-6.
SONG Xiaolin, ZHAI Wanming. Dynamic stress distribution of the infrastructure of CRTSⅡ slab ballastless track under high speed moving load[J]. China Railway Science, 2012, 33(4): 1-6.
[12] 王平, 徐浩, 陈嵘, 等. 路基上CRTSⅡ型板式轨道裂纹影响分析[J]. 西南交通大学学报, 2012, 47(6): 929-934.
WANG Ping, XU Hao, CHEN Rong, et al. Effects analysis of cracking of CRTSⅡ slab track on subgrade[J]. Journal of Southwest Jiaotong University, 2012, 47(6): 929-934.
[13] 铁建设函[2005]754号, 客运专线无碴轨道铁路设计指南[S].
TJSH [2005] No.754, The design guide for ballastless track on passenger dedicated line[S].
[14] 翟婉明. 车辆-轨道耦合动力学[M]. 3版. 北京: 科学出版社, 2007.
ZHAI Wanming. Vehicle-Track coupling dynamics[M]. 3rd ed. Beijing: Science Press, 2007.
[15] 王逢朝, 夏禾, 吴萱. 列车振动对环境及建筑物的影响分析[J]. 北方交通大学学报, 1993, 24(3): 13-17.
WANG Fengchao, XIA He, WU Xuan. Vibration effects of train on surrounding environments and buildings[J]. Journal of Northern Jiaotong University, 1993, 24(3): 13-17.
[16] 林龙. 冲击载荷作用下纤维砼的动力特性实验研究[D]. 广州: 暨南大学理工学院, 2011: 5-7.
LIN Long. Experimental study on dynamic properties of fiber reinforced concrete under impact loading[D]. Guangzhou: Jinan University. College of Science & Engineering, 2011: 5-7.
(编辑 陈爱华)
收稿日期:2013-08-17;修回日期:2013-11-24
基金项目:国家重点基础研究发展计划(“973”计划)项目(2013CB036202);国家自然科学基金资助项目(51008258)
通信作者:王平(1969-),男,湖北宜昌人,教授,从事高速重载轨道结构及轨道动力学研究;电话:13608007071;E-mail:wping@home.swjtu.edu.cn