J. Cent. South Univ. (2012) 19: 2663-2673 

DOI: 10.1007/s11771-012-1325-6

Rapid assessment of regional superficial landslide under heavy rainfall

FANG Wei(方薇)¹, T. Esaki²

1. Key Laboratory of Road Structure and Material of Ministry of Transport

(Changsha University of Science and Technology), Changsha 410004, China;

2. Research Institute for East Asia Environments, Kyushu University, Fukuoka 819-0395, Japan

? Central South University Press and Springer-Verlag Berlin Heidelberg 2012

Abstract: In order to establish a rapid method for regional slope stability analysis under rainfall, matric suction and seepage force were taken into account after obtaining explicit solution of infiltration depth. Moreover, simplified analysis model under 3D condition was put forward based on identification and division of slope units, as well as modification of sliding direction of each column. The result shows that explicit solution of infiltration depth is of good precision; for the given model, safety factors without taking seepage force into account are 1.82-2.94 times higher; the stagnation point of slope angle is located approximately in the range of (45°, 50°); the safety factor changes insignificantly when wetting front is deeper than 2 m; when matric suction changes in the specified range, the maximum variations of safety factor are less than 0.5, which proves that matric suction plays an insignificant role in maintaining slope stability compared to the slope angle and infiltration depth. Incorporated with geographic information system, a practical application of regional slope stability assessment verifies the applicability of the proposed method.

Key words: weathered soil; infiltration model; seepage force; safety factor; geographic information system (GIS)

1 Introduction

Rainfall is one of the most significant triggering factors for slope failure occurrence in mountainous regions, resulting in threat or damage to lives and properties, as well as traffic blocks [1]. With the deepening of wetting front, rainfall leads to following effects: 1) Matric suction decrease, and resulted reduction of shear strength (especially cohesion); 2) Increase of unit weight as moisture content of soil; 3) Lubrication of potential sliding surface and erosion of slope surface; 4) Hydrostatic pressure or hydrodynamic pressure. Due to the close relationship between rainfall and slope failures, it is important to understand the triggering mechanism of rainfall-induced slope failures.

Experience has shown that many slope failures occur during or shortly after heavy rainfall, as water infiltrates into the slope. These failures are characterized by relatively shallow sliding surfaces (typically 1-3 m in depth) that develop parallel to the original slope. The groundwater table is usually located at considerable depth below ground surface and there is no evidence that heavy rainfall causes a rise in the water table sufficient to trigger these shallow failures. Instead, these failures may be attributed to the deepening of a wetting front into the slope due to rainfall infiltration [2-3].

Nowadays, there are mainly two kinds of methods in slope stability analysis under rainfall: empirical probabilistic method and deterministic method. The former method is based on statistical correlation of historical records of landslide occurrences under rainfall; on the other hand, the latter approach constructs a simplified infiltration model to simulate the natural process. Though empirical methods are important, they provide no theoretical framework for understanding how hydrologic processes influence the location and timing; besides, a model established for a specific site is generally unreliable for application to a different site due to variations of geotechnical conditions and climates [4]. Consequently, further research on the triggering mechanism and corresponding deterministic model will certainly be beneficial to the prediction and prevention of rainfall-induced slope failures.

During the past few decades, many analytical and numerical solutions to the unsaturated flow equation have been developed; however, one-dimensional infiltration model remains in widespread use due to its widely accepted concepts of soil physics and simplicity [5]. Moreover, deterministic modeling of slope stability over broad regions typically relies on one-dimensional infinite-slope stability analyses applied over digital topography [6-13]. Infinite-slope stability analysis assumes that landslides are infinitely long and it is most appropriate for analysis of landslides with planar failure surfaces that have a small landslide depth compared to their length and width.

Managing hazards associated with shallow landslides requires an understanding where and when such landslides may occur, and how widespread a potential shallow failure event might be. In recent years, the wide availability of GIS and digital topographic data have led to development of various analytic methods for estimating potential hazards from shallow, rainfall- triggered landslides over large areas [14-15]. Both numerical and analytical techniques have been applied with GIS-based slope stability models to map areas that are potentially unstable during rainfall.

In this work, an explicit solution of infiltration depth under heavy rainfall is derived from Green-Ampt and Philip infiltration model, through which we can get infiltration depth by specifying rainfall duration. Subsequently, with taking seepage force into consideration, safety factor could be obtained based on infinite slope model. Three-dimensional slope stability analysis could be achieved by adjusting the sliding direction of each column. With the help of GIS, by integrating above-mentioned models, the time of failures and expansion of potential sliding areas can be forecast by mapping the variant distribution of safety factors during rainfall.

2 Infiltration model

During rainfall, water infiltrates the soil from the surface and redistributes in the unsaturated zone. The distribution process depends upon the soil moisture conditions, water pressure, and unsaturated permeability. The infiltration capacity (i), which is a measure of the maximum rate at which water can enter the soil, varies throughout a rainfall event. It is controlled mainly by the permeability and water content of the soil and the topography of the slope. Generally, in unsaturated slopes, the infiltration capacity is initially high as large suction pressures are present which compensate for the relatively low unsaturated permeability of the soil. As infiltration continues, the in situ suction and i reduce. The infiltration rate (I) is the rate of water supply to the slope, which is equal to or less than the rainfall intensity [16].

As Fig. 1 shows, rainfall infiltration process roughly consists of two parts. At the initial stage of low intensity rainfall or when the initial infiltration capacity is high, water infiltrates into the soil without runoff (parts a and a′). As the storage capacity of the soil is approached, run-off begins (part b). The time at which run-off starts is affected by antecedent rainfall and initial water content (suction). Given constant initial water content, the higher the rainfall intensity is (>I_r), the earlier the runoff occurs (1). Finally, the infiltration rate converges at saturated permeability. In situ tests indicate that during heavy rainfall, the slope surface becomes complete wet in very short time (usually 0.5-1 h) and remains wet after that unless rain stops. Plenty water supply during heavy rainfall is taken as a basic consideration in follow-up study.

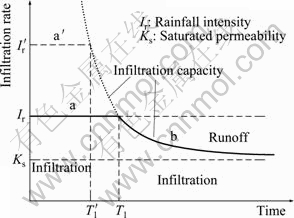
Fig. 1 Relationship between infiltration rate and duration

Green-Ampt model, as one-dimensional infiltration model which is based on capillary theory, was proposed in 1911. It still remains popular because of its succinct concept of “piston” wetting front and the inclusion of soil suction head and hydraulic conductivity parameters. Since 1970s, Green-Ampt model has been widely used in different situations such as inhomogeneous soil and uneven initial water content distribution and satisfying results have been obtained, especially within strong weathered soils.

Four assumptions are made in Green-Ampt model: 1) Soil surface is maintained constantly wet by water ponding; 2) A sharp wetted front exists; 3) The hydraulic conductivity is constant through the soil; 4) The soil matrix suction at the front remains constant. As a result, soil is fully saturated from the surface to the depth of the wetting front, while the soil below the wetting front is of the initial saturation. According to Darcy’s law, neglecting the depth of ponding water, the infiltration capacity of the soil can be given by

                                (1)

The depth of wetting front can be related to the cumulative amount of infiltrated water by

                               (2)

where i is the infiltration capacity (cm/min); I is the cumulative infiltration into unit area (cm); k_s is the permeability of saturated soil (cm/min); z_f is the wetting front depth (cm); h_f is the matric suction at the wetting front (cm); θ_s and θ_i are sated volumetric water content (cm³/cm³) and initial volumetric water content (cm³/cm³), respectively.

In Philip’s one-dimensional infiltration model, infiltration capacity at any specified time can be stated as

                              (3)

where constant A could be regarded equal to k_s, namely:

                              (4)

In Eq. (3) and Eq. (4), S is the total soil water sorptivity (cm/min^0.5); t is the infiltration time (min).

Combining Eq. (1) and Eq. (4), we get

                       (5)

Consequently,

                              (6)

As we know, macroscopic capillary length of soil, λ_c [17], also called “critical pressure” or “half-suction length”, is applied universally as an index of soil calibration; moreover, the concept provides an important tool for the comparative study of hydraulic conductivity or diffusion rate of unsaturated soils. It could be calculated by

                (7)

where ψ_n and ψ₀ are the upper and lower bounds of soil matric suction (ψ_n>ψ₀), respectively, and k(ψ) presents the hydraulic conductivity corresponding to a specified ψ. When initial volumetric water content θ_i is rather low, k(ψ_n)≈0 can be adopted. As a result, Eq. (7) is simplified to be

                       (8)

In saturated area above wetting front of the Green-Ampt infiltration model, ψ₀=0.

SWARTZENDRUBER [18] suggested that the suction at the wetting front h_f in Green-Ampt model can be denoted as

                       (9)

So we get

h_f=λ_c                                      (10)

WHITE and SULLY [19] suggested another expression of macroscopic capillary length:

                            (11)

where S is the total soil water sorptivity (cm/min^0.5); Δθ=θ(ψ₀)-θ(ψ_n) and Δk=k(ψ₀)-k(ψ_n); b is a constant which relies on the shape of water diffusion rate function, locating in a range of [0.5, π/4].

Considering Eq. (11), when soil is saturated after infiltration, the total soil water sorptivity S can be derived by h_f as

                             (12)

Comparing Eq. (6) with Eq. (12), we have

                           (13)

Consequently, infiltration depth at specified time t could be explicitly stated as

                          (14)

Based on infiltration depth, cumulative infiltration and infiltration capacity can be denoted as

            (15)

                      (16)

For an example given by ZHANG et al [20], the results of cumulative infiltration and infiltration capacity obtained from Eqs. (15) and (16) are compared with lab test results in reference, as shown in Fig. 2. It can be seen that the results obtained from explicit solutions of this work agree quite well with the lab test results of original reference.

3 Stability of infinite slope

3.1 Consideration of seepage force

In traditional slope stability analysis models, hydrostatic pressure is taken into account for safety factor calculation while hydrodynamic pressure (seepage force) is always neglected. Seepage force, as a resultant force of thrust, friction and haulage acting on soil skeleton, actually exists in slope. In natural slopes with infiltration, flow net is necessary in determination of the seepage force; however, it is quite difficult to portray by using analytical methods. Consequently, consideration of seepage force in slope stability analysis is restricted in applications. Fortunately, for infinite slope model, seepage force would turn to be easily taken into consideration. As shown in Fig. 3, a slice is selected as study object, on which the inter-slice forces are neglected for simplification. Consider that rainfall infiltrates vertically downward, and consequently, the lower surface of saturated soil is parallel to the upper surface of soil.

Direction of seepage force is the same with rainfall infiltration, namely vertically downward. Therefore, only forces with vertical components are involved in analysis, along the vertical direction:

(17)

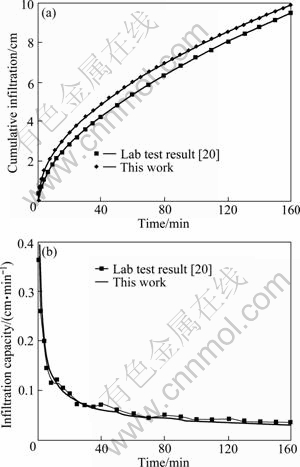
Fig. 2 Comparison of proposed solutions with lab test in reference: (a) Cumulative infiltration; (b) Infiltration capacity

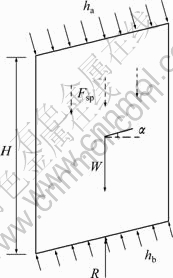
Fig. 3 Seepage force analysis diagram

Consequently,

                   (18)

Based on infiltration theory, we have

                            (19)

So, Eq. (18) could be rewritten as

   (20)

Symbols in above equations and the figure are listed as follows: A_c is the horizontal cross-sectional area of slice, A_c=1; H is the depth of infiltration; α is the inclination angle of upper and lower surfaces of soil; h_a and h_b are the total hydrostatic pressures acting on upper and lower surfaces, respectively; Δh is the total difference of water head; R is the reaction force acting on lower surface; W is the soil weight; F_sp is the seepage force; γ_w is the unit weight of water; γ_sat and γ′ are the saturated weight and floating weight of soil, respectively.

From Eq.(20), we know that reaction force on lower surface includes two parts: one caused by soil floating weight above the wetting front; the other, which is in direct proportion to the total difference of water head Δh, is caused by infiltration. For cases without infiltration, Δh=0 and consequently R=γ′AH, which indicates that the reaction force on lower surface will be equal to the floating weight of soil mass.

For Green-Ampt infiltration model, neglecting the depth of ponding water, we have

                (21)

Then, seepage force (F_sp) can be calculated by

                          (22)

3.2 Safety factor calculation

Effective stress, which controls mechanic properties such as volumetric strain and shear strength, is usually adopted in saturated soil. Unfortunately, it seems incompetent to use a single variable such as effective stress to illustrate the stress status of unsaturated soil. Shear strength of unsaturated soil varies with the degree of saturation. Empirical formulas are established in different areas and put in local application, most of which use saturation degree or volumetric water content as control parameters in infiltration and slope stability analysis by applying total stress method [21-22].

As a result, researchers try to divide “effective stress” into two independent variables. FREDLUND (1978) suggested an extended Mohr-Coulomb failure criterion to determine the shear strength of unsaturated soils:

      (23)

where τ_f is the shear strength of unsaturated soil; c′ and φ′ are effective cohesion and effective friction angle of sated soil, respectively; σ_n is the total normal stress on the failure plane; u_a and u_w are pore pressures of air and water, respectively; (σ_n-u_a)_f is the net normal stress on sliding surface; (u_a-u_w)_f is the matric suction on sliding surface; φ^b is the friction angle attributed by the matric suction.

When soil is nearly saturated, u_w will approach u_a and Eq. (23) will be the same with the shear strength calculation formula of sated soil. Researches show that φ^b is always smaller than (sometimes equal to) φ′. The third term of the formula represents an apparent cohesion of the soil which varies with matric suction. The larger the matric suction is, the higher the value of the apparent cohesion is, and consequently, the higher the available shear strength of soil is.

When rainfall infiltrates through superficial unsaturated zone of slope, the development of wetted zone will lead to the decrease of matric suction and finally cause sliding. Assume that slope failures under heavy rainfall occur along the lower surface of saturated soil mass, which are usually characterized by shallow sliding (typically 1-3 m in depth). A simple infinite slope model is adopted to calculate the factor of safety. As shown in Fig. 4, the safety factor taking seepage force into account could be calculated as

(24)

Under considering Eq. (22), Eq. (24) could be rewritten as

          (25)

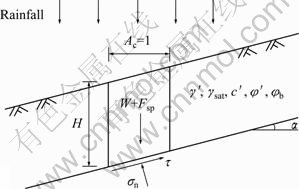
Fig. 4 Infinite slope model of unsaturated soil

To evaluate the influence of seepage force in slope stability, for a given slope model, comparative study was performed. The parameters are partially listed in Table 1, besides which the matric suction of the wetting front   h_f =0.5m. With the development of infiltration depth, the relationship curves between safety factor and infiltration depth, corresponding to slope angle of 30°, 45°, 60°, respectively, are plotted in Fig. 5.

Table 1 Parameters of soil

From Fig. 5, we know that under the same specified conditions, safety factors without taking seepage force into account are much higher (approximately 1.82-2.94 times). Assessment based on results with seepage force not involved would easily tend to overestimate the slope stability and slopes may fail beyond anticipation. Since the seepage force plays such an important role in safety factor calculation, it is reasonable and necessary to take seepage force into consideration in slope stability analysis, especially under heavy rainfall.

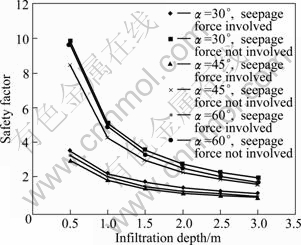
Fig. 5 Influence of seepage force in safety factor calculation

3.3 Influence of parameters

In order to assess the influence of different parameters, such as slope inclination α, infiltration depth H and matric suction of wetting front h_f, comparative analysis was performed based on afore-mentioned model. The basic parameters in Table 1 were adopted and results are shown in Fig. 6.

For the analysis of influence of inclination of slope on the safety factor, slope angle was set to vary from 10° to 60° with a series of matric suction and infiltration depth values, as shown in Fig. 6(a). It could be seen that for any set of parameters, the trends of relationship curves between the safety factor and slope angle are apparently the same. At the initial stage, safety factor reduces sharply when slope becomes steeper. With slope angle keeping on increasing, the reducing rate of safety factor goes to be slower. At the rear part of curves, the safety factor appears to have a small increment as slope angle increases. The stagnation point of slope angle is located approximately in the range of (45°, 50°), which indicates that slope with such an inclination possesses the worst stability. When inclination becomes either flatter or steeper than the stagnation angle, the slope will be safer.

Figure 6(b) indicates that for given slope angle and matric suction on the wetting front, the safety factor decreases with the increase of infiltration depth. The trend of these curves seems similar to the relationship curves between safety factor and slope angle. It should be noted that although decreasing rate of safety factor slows down as infiltration depth develops, there is no stagnation point on each curve and safety factor monotonically reduces until slope failure finally occurs. The safety factor changes insignificantly when wetting front is deeper than 2 m.

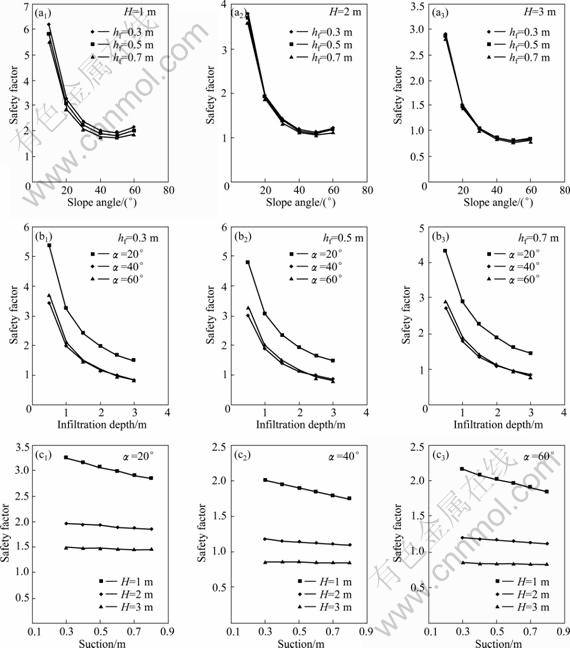
Fig. 6 Influence of different parameters on safety factor: (a) Inclination of slope; (b) Infiltration depth; (c) Matric suction

The influence of matric suction on slope stability can be reflected by Fig. 6(c). For all cases, the results show that safety factor reduces nearly linearly with the increase of matric suction on wetting front. When matric suction changes in the specified range, the maximum variations of safety factor are 0.42, 0.27 and 0.31, respectively, corresponding to the slope angles of 20°, 40° and 60° with an infiltration depth of 1 m. Moreover, all curves appear to be relatively flat, which means that safety factor varies moderately, and consequently, matric suction plays an insignificant role in maintaining slope stability compared to the slope angle and infiltration depth.

4 Three-dimensional slope stability analysis based on GIS

Geographic information system (GIS) has been used more and more widely in assessment of natural disasters because of its powerful functions of management, manipulation and illustration of multiple spatial data.

As shown in Fig. 7, for a slope failure mass, by using the GIS spatial analysis tools, the slope-stability-related data of the whole study area can be represented as the GIS vector layers. For each layer, a grid-based layer can be obtained by using the GIS spatial analysis function and the grid size can be set with the requisite precision. All original data (such as elevation, inclination, slope, groundwater, strata, slip surface, and mechanical parameters) for the 3D safety factor calculation are available with respect to each grid cell by dividing the study mass into small soil columns. After inputting these data into a deterministic model of slope stability, a value of safety factor can be derived.

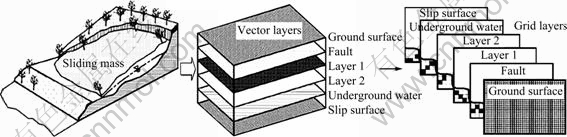
Fig. 7 Failure mass and its expression in GIS

To apply the 3D method to actual regional landslide hazard assessment, one more important problem needed to be solved is the suitable extraction of the study objects (or study units) from a mountainous area. This term refers to a portion of the land surface which contains a set of ground conditions different from the adjacent units across definable boundaries. In other words, a mapping unit represents domain that maximizes internal homogeneity and external heterogeneity. Various methods, which could be classified into four categories as presented in Table 2, are proposed to partition the landscape for landslide hazard assessment and mapping.

Table 2 Comparison of main methods to partition mountainous area [14]

It seems that slope unit is the most appropriate object for landslide hazard mapping because of similar topographic/geological characteristics inside and a clear physical relationship between landslides and the basic morphological elements. Slope units can be regarded as either side of a sub-basin of any order into which a watershed can be partitioned, and can be identified topologically by a ridge line and a valley line. Using the hydraulic model tool of GIS, the watershed polygons of the study area can be obtained easily from digital elevation model (DEM) file. Topologically, the outline of the watershed polygon can be considered as the ridge line. In order to search the valley line, the reversed DEM is used. By repeating the same operations, valley line could be obtained as the boundary of the reversed watershed polygon. Consequently, the valley line divides the former watershed polygon into two slope units, as demonstrated in Fig. 8.

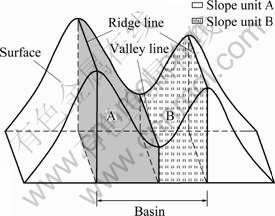
Fig. 8 Partition of slope units

By statistical calculation of spatial features of all pixels in a slope unit, its topographical characteristics, such as inclination direction, inclination angle and slope height, can be obtained immediately. As shown in Fig. 9, due to the homogeneous topography of slope units, the values of both slope angle and aspect of pixels in the range of slope unit present a normal distribution. Therefore, the main inclination angle and main aspect of a slope unit can be acquired by statistical calculation for the mean value of the normal distributed raster data.

Since “aspect” characterizes the direction with steepest inclination of a column, the main aspect of all columns in a slope unit is considered to be the sliding direction. Sliding direction of all columns within sliding mass, composed of many columns, are the same because they slide as a whole. However, aspects of most columns vary moderately, thus they intersect main aspect with an angle. Combining Fig. 9 and Table 3, we know that sliding aspects corresponding to columns 1 and 2 are slightly different from the main aspect of the whole slope unit A. Obviously, as Fig.10 shows, arrows A indicate the direction of the main aspect of slope unit A; on the other hand, arrows of A₁ and A₂ represent the aspects of columns 1 and 2, respectively. In Fig. 10, Δδ₁ and Δδ₂ are differences between A₁, A and A₂, A, respectively.

Fig. 9 Statistical calculation of columns within slope units

Table 3 Aspect of slope unit and columns

Fig. 10 Aspect arrows

As a study case, the spots in Fig. 11 represent the columns with the angle larger than 90°, which denote an opposite sliding direction compared to the whole sliding mass. It can be seen that these columns distribute along boundary of slope units or near the faults. Consequently, these few columns would not affect the result of slope stability analysis. With considering the difference of sliding direction between each column and the entire sliding mass, the safety factor calculation should be modified as

   (26)

where Δδ is the difference of sliding direction between pixel and corresponding slope unit.

Fig. 11 Discontinuous spots

5 A practical application of regional slope stability analysis

The study area is in Dazaifu District, Fukuoka, Japan. Figure 12 shows the hillshade, from which we can see that highway is located on the left side of the hill. Observation data have shown frequent failures of soil slope in this area, most of which are characterized by shallow sliding during or shortly after heavy rainfall. In order to evaluate the regional changes of slope stability caused by heavy rainfall and to make a forecast for potential slope failures, GIS was incorporated with aforementioned models and landslide mapping was obtained.

Initially, aerial survey was performed and elevation data were acquired. After necessary data procedures by using spatial analysis tool of GIS, raster file of digital elevation model (DEM), with resolution of 5 m, was obtained. Subsequently, topographic data such as slope angle and inclination direction, which are requisite in later analysis, would be available. Properties of upper layer under rainfall in study area are given in Table 4, in which w and w_s are initial and saturated water contents of soil.

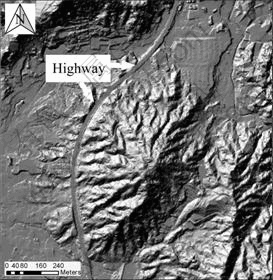
Fig. 12 Hillshade of study area

Table 4 Geotechnical and hydraulic parameters of surficial soil

This work was to evaluate potential slope failures which might be harmful to the highway; consequently, spatial analyst tools were used to identify research range in which sliding mass moved towards the highway before partition of slope units. After slope failure occurs, sliding mass always moves down across slope surface or along valleys until it stops. Whatever the moving path is, the sliding mass seldom moves over ridges because of insignificant speed. Therefore, the mountainous area could be divided into two parts by ridge lines: one part where the sliding mass might cause risks to the traffic safety and the other part where the sliding mass would not move towards the highway when slope failure occurs, which was not taken into account in following study. As Fig. 13 shows, the masked area presents the final range of potentially dangerous slopes in which region A, as step surface, is also included. Furthermore, slope unit division is completed, as given in Fig. 14.

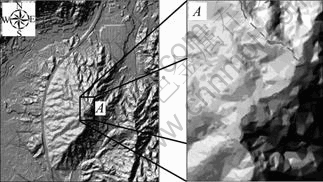
Fig. 13 Study area identification

Fig. 14 Partition of slope units

As mentioned earlier, sliding direction of different slope units is shown in Fig. 15, which demonstrates a clear physical relationship between landslide phenomenon and slope units.

Fig. 15 Example of sliding direction of slope units

Figure 16 illustrates four distribution maps of safety factor under lasting rainfall. From these maps, a high correlation between rainfall duration and the decrease of safety factor can be recognized. As Fig. 16 shows, with the prolonging of heavy rainfall, the stability situation of the study area becomes worse. Safety factor reduces gradually and final potential sliding area extends significantly compared to the initial stage. The potential sliding area, with a safety factor smaller than 1.0, appears extensively during 24-36 h.   

By combining different thematic maps, more information or details might be acquired, such as land use or residential distribution, and then comprehensive assessment based on these data would definitely be beneficial to sliding prevention and disaster treatment in this area, as well as prediction of affecting range of potential sliding.

Fig. 16 Deterioration of regional slope stability under rainfall: (a) After 12 h; (b) After 24 h; (c) After 36 h; (d) After 48 h

6 Conclusions

1) A rapid method for evaluating the variation of surficial slope stability during heavy rainfall is proposed, in which the infiltration depth is explicitly expressed by time and the seepage force is taken into account. Safety factor calculation with considering the difference of sliding direction between each column and corresponding slope unit becomes more reasonable.

2) Comparative study shows that seepage force is quite important in slope stability calculation. Without consideration of seepage force, the safety factor would be 0.82-1.94 times higher, and therefore it is necessary to take seepage force into consideration.

3) Study on influence of parameters is performed, which shows that safety factor reduces monotonically as infiltration depth increases, and nearly linearly when the matric suction on wetting front increases. With the growth of slope angle, safety factor initially reduces sharply and subsequently slows down; finally there is a marginal increase of safety factor. The stagnation point of slope angle is located approximately in the range of (45°, 50°).

4) Due to the powerful and comprehensive functions of management, manipulation and illustration of multiple and massive spatial data, GIS is implemented to perform a practical application of regional slope stability analysis, which verifies the applicability of the proposed method. Distribution variation of safety factors with lasting rainfall is portrayed intuitively, and such a spatio-temporal hazard map of rainfall-induced landslide would be important for hazard prediction and treatment.

5) It should be noted that the present work is focused on evaluating the influence of infiltration. Other effects, such as antecedent precipitation and run-off, which can influence the capacity and the amount of infiltration significantly, should be considered in future work.

References

[1] LEE M L, NURLY G. A simple model for preliminary evaluation of rainfall-induced slope instability [J]. Engineering Geology, 2009, 108: 272-285.

[2] KIM J, JEONG S. Influence of rainfall-induced wetting on the stability of slopes in weathered soils [J]. Engineering Geology, 2004, 75: 251-262.

[3] ZHOU Zhong, WANG Hong-gui, FU He-lin. Influences of rainfall infiltration on stability of accumulation slope by in-situ monitoring test [J]. Journal of Central South University of Technology, 2009, 16(2): 297-302.

[4] RICHARD M. Landslide triggering by rain infiltration [J]. Water Resources Research, 2000, 36(7): 1897-1910.

[5] SUNG E. Infiltration analysis to evaluate the surficial stability of two-layered slopes considering rainfall characteristics [J]. Engineering Geology, 2009, 105: 32-43.

[6] MONTGOMERY D R, DIETRICH W E. A physically-based model for the topographic control on shallow landsliding [J]. Water Resources Research, 1994, 30(4): 1153-1171.

[7] WU W M, SIDLE R C. A distributed slope stability model for steep forested basins [J]. Water Resources Research, 1995, 31(8): 2097-2110.

[8] BORGA M, FONTANA G D. Shallow landslide hazard assessment using a physically based model and digital elevation data [J]. Environmental Geology, 1998, 35(2/3): 81-88.

[9] BAUM R L, SAVAGE W Z, GODT J W. TRIGRS: A Fortran program for transient rainfall infiltration and grid-based slope-stability analysis [R]. U.S. Geological Survey Open-File Report, 2002.

[10] CASADEI M, DEITRICH W E, MILLER N L. Testing a model for predicting the timing and location of shallow landslide initiation in soil-mantled landscapes [J]. Earth Surface Processes and Landforms, 2003, 28: 925-950.

[11] SAVAGE W Z, GODT J W, BAUM R L. A model for spatially and temporally distributed landslide initiation by rainfall infiltration. [M]// RICKENMANN D, CHEN L, Eds. Debris flow hazards mitigation: Mechanics, prediction and assessment. Rotterdam: Mill Press, 2003.

[12] HARP E L, MICHAEL J A, LAPRADE W T. Shallow-landslide hazard map of Seattle, Washington [R]. U.S. Geological Survey Open-File Report, 2006.

[13] GODT J W, BAUM R L. Transient deterministic shallow landslide modeling: Requirements for susceptibility and hazard assessments in a GIS framework [J]. Engineering Geology, 2008, 102: 214-226.

[14] CARRARA A, CARDINALI M, GUZZETTI F. GIS technology in mapping landslide hazard. Geographical information systems in assessing natural hazards [M]. Dordrecht: Kluwer Academic Publisher, 1995.

[15] QIU C, ESAKI T, ZHOU G Y, XIE M W. Development of GIS-based intelligent slope units identifying tool for 3D slope stability evaluation [C]// International Workshop on Earth Science and Technology. Kyushu University, Japan, 2003: 115-122.

[16] GAVIN K, XUE J F. A simple method to analyze infiltration into unsaturated soil slopes [J]. Computers and Geotechnics, 2008, 35: 223-230.

[17] PHILIP J R. Reply to “comments on “steady infiltration from spherical cavities”” [J]. Soil Sci, 1985, 49: 788-789.

[18] SWARTZENDRUBER D. Derivation of a two-term infiltration equation from the Green-Ampt model [J]. Journal of Hydrology, 2000, 236: 247-251.

[19] WHITE I, SULLY M J. Macroscopic and microscopic capillary length and time scales from field infiltration [J]. Water Resource Research, 1987, 23: 1514-1522.

[20] ZHANG Zhen-hua, PAN Ying-hua, CAI Huan-jie. Approximate explicit solution to infiltration rate of Green-Ampt infiltration formula [J]. System Science and Comprehensive Studies in Agriculture, 2006, 22(4): 308-311. (in Chinese)

[21] FREDLUND D G, RAHARDJO H. Soil mechanics for unsaturated soils [M]. New York: Wiley, 1993.

[22] WU Hong-wei, CHEN Shou-yi, PANG Yu-wei. Parametric study of effects of rain infiltration on unsaturated slopes [J]. Rock and Soil Mechanics, 1999, 20(1): 1-13.

(Edited by YANG Bing)

Foundation item: Project(kfj110207) supported by Open Fund of Key Laboratory of Road Structure and Material of Ministry of Transport, China

Received date: 2011-08-30; Accepted date: 2011-12-02

Corresponding author: FANG Wei, PhD; Tel: +86-18229987992; E-mail: fangwei5642366@163.com