采用R410A的变频房间空调器的理论与实验研究
曹小林，喻首贤，李雄林，王伟，廖胜明
(中南大学 能源科学与工程学院，湖南 长沙，410083)
摘 要：对采用R410A和直流变频涡旋压缩机的房间空调器的节能特点进行分析。采用分布参数法建立该种空调器的稳态数学模型，运用该模型计算制冷量、功率和能效比随运行频率变化的趋势，并在中南大学空调器性能试验台上测试该空调器的性能。研究结果表明：制冷量、功率和能效比的平均相对误差分别为2.9%，6.2%和3.9%，模型基本可靠；变频空调器在20 Hz运行时能效比高达4.3，而在100 Hz运行时能效比低于2.5，因此，在选用变频空调器时，应选择制冷量较大的空调器，避免超频运行。
关键词：房间空调器；涡旋压缩机；直流变频；制冷剂R410A
中图分类号：TB663 文献标志码：A 文章编号：1672-7207(2010)02-0759-05
Theoretic and experimental study on domestic air-conditioner with R410A as refrigerant
CAO Xiao-lin, YU Shou-xian, LI Xiong-lin, WANG Wei, LIAO Sheng-ming
(School of Energy Science and Engineering, Central South University, Changsha 410083, China)
Abstract: The energy-saving characteristic of R410A air conditioner with DC-inverter scroll compressor was analyzed. A parameter-distributing steady mathematic model was established for this air conditioner. With this model, the trend changing with operating frequency of refrigeration capacity, power input and energy efficiency ratio (EER) was calculated. This air conditioner was tested on the air conditioner performance-testing bench in Central South University. The results show that the relative errors of capacity, power and EER are 2.9%, 6.2%, 3.9% respectively, which verifies that the model established is reliable. For a domestic air conditioner with DC-inverter, EER can reach 4.3 when operating at 20 Hz, but lower than 2.5 when operating at 100 Hz, so it is advised to choose one with higher refrigeration capacity air conditioner with DC-inverter.
Key words: domestic air-conditioner; scroll compressor; DC-inverter; R410A
环保、高效、节能已成为未来空调发展的方向，因而空调行业必然将采用环保制冷剂和高效节能型器件。环保制冷剂R410A作为R22的替代品用于空调已经得到重视[1-2]。变频空调器是一种新型节能机种。王起霄等[3]对变频空调的性能进行了研究分析；陈观生等[4]从理论上分析了影响变频空调器能耗的主要因素，即空调器的实际运行工况、压缩机电机效率、压缩机起停次数及变频器的能耗等，得出变频空调器可以节能20%左右；Tassou等[5]对比变容量空调与常规空调的运行情况，认为变频空调节能10%以上；Vargas[6]模拟了定速空调器停开机过程与变速压缩机调节过程，并比较了其能耗；孟岩勇等[7]建立变频空调的动态数学模型，获得EER(Energy efficiency ratio)、制冷量等随室外温度以及运转频率变化的规律，但是，由于模型存在许多不足，变频空调在低频时的计算结果与试验数据差别较大。本文作者针对采用R410A制冷剂和高效直流变频涡旋压缩机的房间空调器建立分布参数稳态数学模型，对该空调器在多种运行频率下的性能进行仿真计算，并在中南大学空调器性能试验台上进行性能测试，将计算结果与实验结果进行对比 验证。
1 数学模型
1.1 压缩机模型
变频压缩机可由变频器控制，通过改变电机运行频率来调节转速。由于电动机与压缩机之间的转差率对模型无影响，因而予以忽略。对于直流变频压缩机，转速n和频率fd之间的关系为[8]：
式中：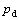
为电动机磁极数。
1.1.1 输气量的计算
涡旋式压缩机的理论输气体积流量qvh为：
式中：Vs，N，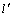
，l和h分别表示吸气容积、压缩腔室对数、涡旋体节距、壁厚和高度。
制冷剂的实际质量流量qmr为：
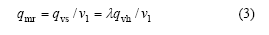
式中：qvs，λ和v1分别为实际输气体积流量、输气系数和吸气质量体积。
1.1.2 压缩机的换热计算
根据热力学第一定律，可以得到如下压缩机热平衡方程式：
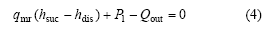
式中：hsuc和hdis分别为压缩机入口焓和出口焓；Qout为压缩机壳体表面放热量；P1为压缩机的电功率。
1.2 换热器模型
1.2.1 控制方程的建立
换热器模型采用稳态分布参数法，根据制冷剂在换热器中的换热和流动情况进行如下假设：
(1) 制冷剂在管路中做一维轴向流动；
(2) 只考虑制冷剂与管壁之间、管壁与空气之间的径向热量交换，不计轴向的热量传递；
(3) 管壁的导热热容忽略不计；
(4) 在两相区制冷剂气体与液体均匀混合；
(5) 忽略不凝性气体、制冷剂侧油膜及空气侧灰尘对传热的影响；
(6) 对蒸发器，不计凝结水膜热容；
(7) 忽略空气和制冷剂的流动阻力损失。
控制体示意图如图1所示，图中：t，x，qm和d分别为温度、干度、质量流量和空气湿度，下标r和a分别表示制冷剂和空气。
图1 控制体示意图
Fig.1 Diagram of control unit
冷凝器和蒸发器控制体的能量方程为：
式中：hr，cpa和rw分别为制冷剂比焓、空气比热容和水的气化潜热。对于冷凝器，?da为0。
变频空调器所用的换热器管内外都采用有效的强化换热措施，如采用波纹形、单面开缝及双面开缝型铝套片以及内螺纹管等，在整体结构布置上采用折弯式等。所有措施都是为了提高换热器的换热面积及换热系数，同时减小换热器外形尺寸，降低系统成本。
1.2.2 冷凝器制冷剂侧换热系数的计算
冷凝器模型采用整体平翅片，换热管采用内螺纹管。实验研究表明[9-10]：内螺纹管内平均凝结换热系数为光管的1.7~2.0倍，凝结换热的阻力系数也增 大，约为光管的1.6~1.9倍，从而提高了制冷剂侧换热系数。
单相区换热系数
计算公式[11]为：
式中：Re为雷诺数；λ为制冷剂的导热系数；di为换热管内径。
两相区的换热系数计算式[12]为：
式中：Pr为普朗特数；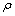
，
和x分别表示制冷剂密度、动力黏度和干度；下标l和v分别表示液相和气相。
1.2.3 蒸发器制冷剂侧换热系数的计算
蒸发器换热管同样为内螺纹管。研究表明：内螺纹管平均对流沸腾换热系数是光管的2.5~3.0倍，而平均阻力是光管的1.3~1.7倍，有效提高了制冷剂侧的换热系数。单相区换热系数计算与冷凝器的计算方法相同。
两相区换热系数采用凯特里卡[13]公式计算：
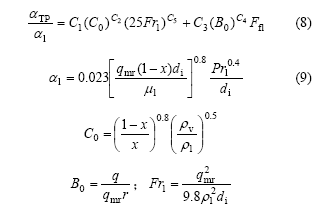
式中：
为两相区换热系数；
为液相单独流过管内的换热系数；q为热流密度；C1，C2，C3，C4，C5和r均为气化潜热；C0，B0为无量纲数；Ffl为取决于制冷剂性质的无量纲数。
1.2.4 空气侧换热系数
蒸发器翅片采用双面开缝翅片，冷凝器采用整体平翅片。双面开缝翅片能破坏低风速下空气流动的层流边界层，并且减小管后部的正压力梯度，使脱离点后移，大大提高了低风速下空气侧的换热效果，在相同风速下，双向开槽翅片当量换热系数比波形片的高，缩小了室内换热器的面积。
双面开槽翅片的当量换热关联式[14]为：
式中：umax，de和v分别为最大迎面风速、当量直径和运动黏度。
整体式翅片换热器的空气侧换热系数[14]为：
式中：L为沿气流方向的肋片长。
1.3 毛细管模型
因为毛细管经济、适用，冰箱和房间空调器多采用毛细管节流[15]，制冷剂在毛细管内的流动模型采用均相模型。动量方程[16]为：
式中：f和u分别为摩阻系数和流速。
2 系统耦合求解
假定压缩机的入口温度Tin、入口压力pin和排气压力pout等参数的初始值，分别调用压缩机模块、冷凝器模块、毛细管模块，比较压缩机的制冷剂流量与毛细管的制冷剂流量，若不满足精度要求，则调整排气压力，直至满足精度要求为止。然后，调用蒸发器模块，计算压缩机入口压力、温度，与假定的入口压力pin、入口温度Tin比较，直至其满足精度要求为止。计算流程图如图2所示。
3 计算结果与实验验证
实验对象为采用R410A和直流变频压缩机的KFR－35GWQ/BM分体空调器，实验在中南大学的空调器性能试验台进行。针对空调系统在制冷运行过程中制冷量、功率和能效比随频率变化而变化的情况进行记录，在空调标准T1制冷工况下，从低频20 Hz到高频100 Hz每10 Hz作为1个区间对各参数的变化进行记录，然后，与模型的仿真结果进行对比验证。
图3~5所示分别为制冷量、功率和能效比的仿真值和实验值的对比结果。由图3~5可以看出：仿真值与实验值的变化趋势基本一致，制冷量、功率和能效比的平均相对误差分别为2.9%，6.2%和3.9%，证明模型基本可靠。
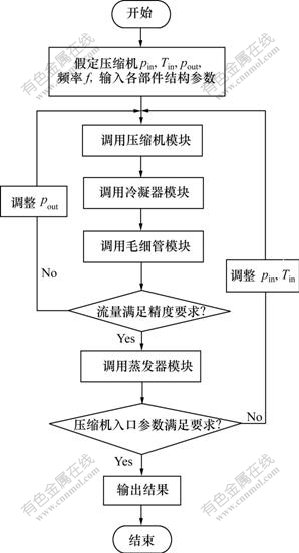
图2 计算流程图
Fig.2 Calculation steps
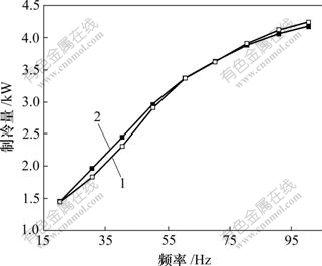
1—实验值；2—计算值
图3 制冷量随频率的变化
Fig.3 Relationship between refrigeration capacity and frequency
1—实验值；2—计算值
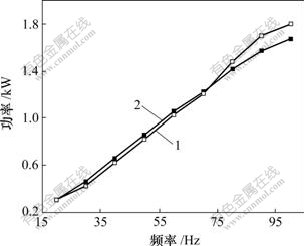
图4 压缩机功率随频率的变化
Fig.4 Relationship between compressor Power and frequency
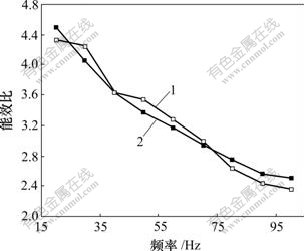
1—实验值；2—计算值
图5 能效比随频率的变化
Fig.5 Relationship between energy efficiency ratio (EER)
and frequency
从图3和图4可以看出：制冷量和功率均随频率的增加而增加。从图5可以看出：该空调器的能效比随频率的增加而降低，这是因为：从式(1)得知，压缩机转速和频率呈正比，而制冷量和功率随压缩机转速增加几乎也呈正比，这意味着蒸发器和冷凝器的传热负荷和相应的传热温差增大，在室内外环境工况不变的情况下，冷凝温度必然升高，蒸发温度必然降低，压力比增大，功率进一步增加，而制冷量则会有所减小，从而使能效比变化较大。
该空调器的运行频率在50 Hz时，能效比约为3.4，达到一级能效；但当运行频率低于50 Hz时，其能效比更高，可以达到4.3以上，这说明变频空调器在低频运行时能够节能。但当运行频率超过50 Hz时，特别是高频运行时，能效比反而比定频空调的低。
4 结论
(1) 建立了采用直流变频涡旋压缩机的R410A变频房间空调器的稳态分布式数学模型。运用该模型得到变频空调器的制冷量、功率和能效比随运行频率的变化趋势。对该空调进行了性能测试，计算结果和实验结果较吻合，制冷量、功率和能效比的平均相对误差分别为2.9%，6.2%和3.9%，模型基本可靠。
(2) 变频空调器的制冷量和功率均随运行频率的增加而增加，而能效比随着频率的增加而降低。在20 Hz运行时，能效比高达4.3，而在100 Hz运行时，能效比低于2.5；所以，应选用制冷量较大的变频空调器，避免超频运行。
参考文献：
[1] 张萍, 陈光明. R410A替代R22制冷系统的实验与分析[J]. 工程热物理学报, 2008, 29(5): 741-746.
ZHANG Ping, CHEN Guang-ming. Experiment and analysis on refrigeration system of R410A replacing R22[J]. Journal of Engineering Thermophysics, 2008, 29(5): 741-746.
[2] 朱明善, 史琳. 国际上限用HCFC类制冷剂的态势与我国对策的建议[J]. 制冷与空调, 2001, 6(1): 1-7.
ZHU Ming-shan, SHI Lin. Trend of HCFCs phase-out in the world and suggestions for our country[J]. Refrigeration and Air-conditioning, 2001, 6(1): 1-7.
[3] 王起霄, 刘淑静. 变频空调的性能研究[J]. 哈尔滨商业大学学报, 2001, 17(3): 69-71.
WANG Qi-xiao, LIU Shu-jing. Study on performance of air conditioner with DC-inverter[J]. Journal of University of Harbin Commerce, 2001, 17(3): 69-71.
[4] 陈观生, 吴桂炎. 家用变频空调器节能分析[J]. 制冷空调与电力机械, 2003, 24(4): 26-29.
CHEN Guan-sheng, WU Gui-yan. Analysis on energy-saving of domestic air conditioner[J]. Refrigeration, Air Conditioning and Electronic Machine, 2003, 24(4): 26-29.
[5] Tassou S A, Marqunand C J, Wilson D R. Comparison of the performance of capacity controlled and conventional ON/OFF controlled heat pumps[J]. Applied Energy, 1983, 5(4): 241-256.
[6] Vargas J V C. Simulation in transient regime of a heat pump with closed-loop and on-off control[J]. International Journal of Refrigeration, 1995, 18(4): 235-243.
[7] 孟岩勇, 南晓红. 完整工作日中变频房间空调器动态特性仿真[J]. 制冷学报, 2007, 28(5): 49-52.
MENG Yan-yong, NAN Xiao-hong. Dynamic simulation on characteristics of an inverter room air-conditioner in a complete working day[J]. Journal of Refrigeration, 2007, 28(5): 49-52.
[8] 周宏坤, 俞诚民. 浅谈直流变频空调器的工作原理[J]. 电机电器技术, 2000, 34(1): 25-28.
ZHOU Hong-kun, YU Cheng-min. A review on the working principle of DC-inverter air conditioner[J]. Technique of Engine and Electric Equipments, 2000, 34(1): 25-28.
[9] Eckels S J. Evaporation and condensation of HCF-134a and CFC-12 in a smooth tube and a micro-fm tube[J]. ASHRAE Trans, 1991, 97: 71-81.
[10] Sami S M, Tulej P J, Song B. Study of heat and mass characteristics of ternary non-azeotropic refrigerant mixtures inside air/refrigerant enhanced surface tubing[J]. ASHRAE Trans, 1995, 101: 1402-1412.
[11] 吴业正. 小型制冷装置设计指导[M]. 北京: 机械工业出版社, 1999: 95-102.
WU Ye-zheng. Guidance on designing small refrigerating apparatus[M]. Beijing: Mechanical Industry Press, 1999: 95-102.
[12] Slugem K. Enhancement of in-tube condensation of non-azeotropic refrigerant mixture with a micro-fin tube[J]. Trans of the JAR, 1993, 10(1): 95-101.
[13] Masaaki T T O, Hideyaki K. Boiling heat transfer and pressure drop in internal spiral-grooved tubes[J]. JSME, 1979, 22: 171-173.
[14] 信育华. 单元式空调机换热器性能的计算模拟与优化[D]. 西安: 西安交通大学能源与动力工程学院, 1994: 45-60.
XIN Yu-hua. Simulation and optimization of heat exchanger for unit air conditioner[D]. Xi’an: School of Energy and Power Engineering, Xi’an Jiaotong University, 1994: 45-60.
[15] 刘益才, 曹立红, 杨智辉, 等. 冰箱毛细管出口气液两相流理论[J]. 中南大学学报: 自然科学版, 2007, 38(3): 450-453.
LIU Yi-cai, CAO Li-hong, YANG Zhi-hui, et al. Theoretical research on gas-liquid two-phase flow at outlet of refrigerator capillary[J]. Journal of Central South University: Science and Technology, 2007, 38(3): 450-453.
[16] 曹小林, 吴业正. 含油制冷剂流过毛细管的流动特性理论模型[J]. 制冷学报, 1999, 30(1): 25-28.
CAO Xiao-lin, WU Ye-zheng. A theoretical model for predicting adiabatic capillary tube performance with refrigerant/oil mixture[J]. Journal of Refrigeration, 1999, 30(1): 25-28.
收稿日期：2008-10-22；修回日期：2009-03-03
基金项目：国家高技术研究发展计划(“863”计划)项目(2007AA05Z225)
通信作者：曹小林(1969-)，男，湖南益阳人，博士，副教授，从事制冷系统热物理过程的研究；电话：13055199692；E-mail: xlcao＠mail.csu.edu.cn
(编辑 刘华森)
