J. Cent. South Univ. Technol. (2011) 18: 1662-1666
DOI: 10.1007/s11771-011-0886-0
A new apparatus for investigating stress, deformation and seepage coupling properties of rock fractures
LIU Cai-hua(刘才华), CHEN Cong-xin(陈从新)
State Key Laboratory of Geomechanics and Geotechnical Engineering, Institute of Rock and Soil Mechanics,
Chinese Academy of Sciences, Wuhan 430071, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2011
Abstract: A true triaxial apparatus which is composed of three units was presented. The apparatus allows for investigations on deformation and seepage behaviors of a single rock fracture subjected to lateral stress and normal stress. The first unit has three jacks which can apply loads independently in three orthogonal directions. The second unit is used to supply water inflow, control seepage pressure and measure flow velocity in real time. The third unit is for measuring the normal deformation of rock fractures. Some tests for investigating the normal deformation and seepage behaviors of rock fractures subjected to normal and lateral loads on hard granite specimens with an artificial persistent fracture, were introduced. The results show that both the normal deformation and the hydraulic conductivity are influenced not only by the normal stress but also by the lateral stress. It is also shown that the aperture and the hydraulic conductivity decrease with the increasing normal stress but increase with the increasing lateral stress and both the aperture and the hydraulic conductivity obey exponential relationships with the normal stress and the lateral stress.
Key words: true triaxial apparatus; rock fractures; normal stress; lateral stress; normal deformation; seepage properties; hydraulic conductivity
1 Introduction
Seepage and stress fields coupling of jointed rock masses in many geotechnical situations such as water conservation, hydropower, high-level radioactive waste disposal, oil reposition and slope engineering, have attracted concentrated attention. Since a rock fracture is the weakest part of rock mass, it is extremely important to investigate the seepage properties of a single fracture to study the hydro-mechanical law of jointed rock masses. It is well known that the aperture of a rock fracture markedly influences the hydraulic conductivity, and the square law which describes a linear relationship between the hydraulic conductivity and the squared aperture, is widely accepted. Investigations on stress, deformation and seepage coupling are of vital importance to understand the hydro-mechanical properties of jointed rock masses.
Many researchers have made significant contributions to this problem. Early studies were focused on normal stress and seepage coupling. SNOW [1] proposed an empirical expression to describe the relationship between the hydraulic conductivity and the normal stress. LOUIS [2] gave a formula revealing the influence of the normal stress on the hydraulic conductivity according to drilling pumping test datum. Similar results were obtained by others [3-11] based on experimental tests. These models indicate that the hydraulic conductivity decreases with the rising of normal stress. Some investigations were directed to normal deformation of a rock fracture under normal stress. GOODMAN [12] obtained an empirical equation and pointed out that the normal deformation is a reciprocal function of the normal stress. BANDIS et al [13] improved the model and further discussed the relationship between hydraulic conductivity and the normal stress. An equation describing the exponential relationship between the normal deformation and the normal stress, proposed by SUN and LIN [14], is widely accepted. Actually, rock masses always lie in a complex stress condition. Accordingly, it is significant to study the seepage properties of rock fractures under the lateral stress as well as the normal stress. However, limited investigations in this field are documented in literatures. ZHANG et al [15] and ZENG et al [16] studied the flow of rock fractures under different stress conditions and pointed out that the flow velocity diminished as the normal stress increased, but rose with the lateral stress increasing. ZHAO et al [17] developed an empirical equation to calculate the hydraulic conductivity subjected to different triaxial stress. Although the above researches greatly promoted the seepage and stress coupling properties of rock fractures, much more investigations are necessary to obtain robust theories.
In this work, a true triaxial device (RPT-3D) designed for studying stress, deformation and seepage properties of rock fractures was presented, and then some tests for investigating the normal deformation and seepage behaviors of a single rock fracture under normal and lateral loads on hard granite specimens with an artificial persistent fracture were introduced.
2 Development of true triaxial apparatus
The true triaxial apparatus shown in Fig.1 consists of three units, including the loading unit, the seepage measurement unit and the deformation measurement unit. It has the following characteristics: 1) loads can be exerted on a fractured rock sample independently along three orthogonal directions, 2) the normal deformation of the joint can be accurately measured, and 3) the seepage pressure can be applied in random and can be kept constant during hydraulic tests.

Fig.1 General view of true triaxial apparatus
2.1 Loading unit
The loading unit including a vertical jack and two horizontal jacks is depicted in Fig.2, which can apply loads independently along three orthogonal directions. One horizontal jack loads a normal stress to the rock fracture, and the other horizontal jack and the vertical jack exert lateral stress parallel to the rock fracture. The jacks fixed on the steel loading box which is rigid enough and equipped with stress meters, can apply 0- 5 MPa normal stress or lateral stress to a rectangular specimen with size of 15 cm×15 cm×28 cm.
2.2 Seepage measurement unit
The RPT-3D having a seepage system is shown in Fig.3, which produces water flow through the rock fracture. The specimen is made by splitting hard granite and hence the fracture is persistent. In order to prepare the specimen and ensure it is leakproofed on the sides parallel to the flow direction, two notches of 0.5 cm in depth and 0.5 cm in width were cut into the two parallel sides of the specimen and filled with silicon paste. Therefore, the effective size of the fracture surface is 14 cm×28 cm.
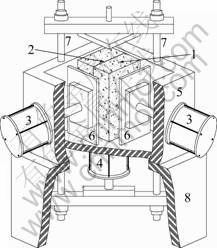
Fig.2 Schematic map of loading unit: 1—Specimen; 2—Rock fracture; 3—Horizontal jacks; 4—Vertical jack; 5—Steel loading box; 6—Pressure plates; 7—Tension rods; 8—Support frame
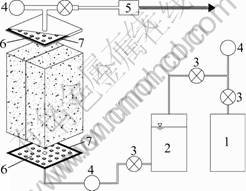
Fig.3 Sketch of water flow though rock fracture: 1—High- pressure nitrogen tank; 2—Water tank; 3—Valves; 4—Pressure meters; 5—Flowmeter; 6—Flow-guided grids; 7—Seal rings
Hydraulic pressure was applied using stable high-pressure nitrogen which is controlled through a compressor valve. Water flows through the fracture from the bottom to the top of the specimen which is seated on and covered by two steel plates with flow-guided grids respectively. Two valves are respectively set at the inlet and the outlet to accurately control seepage pressure and flow velocity through the fracture. Water current was measured by a flowmeter.
2.3 Deformation measurement unit
According to Darcy Law, hydraulic conductivity increases with rising the squared aperture. The aperture is a key factor which affects the stress and seepage coupling properties of rock fractures. In order to monitor the normal deformation of a rock fracture subjected to normal or lateral loads, four strain gauges are symmetrically embedded in the two notches and connected to a data acquisition instrument by wires, as depicted in Fig.4. The stable values of four strain gauges are collected by the data acquisition instrument and the average value represents the normal deformation/ aperture increment of the rock fracture.
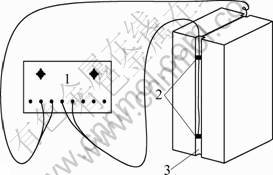
Fig.4 Normal deformation measurement of rock fractures: 1— Data acquisition instrument; 2—Strain gauges; 3—Notches cut for creating a persistent fracture
2.4 Specimen
The granite used to prepare the specimen is from Daye in China, with the unit weight of 26.7 kN/m3 and the uniaxial compressive strength of 136 MPa. All six faces of the specimen were polished with smoothness of 0.5 mm, dimension error of ±0.3 mm and angle error of ±0.25°. Two notches of 0.5 cm in depth and 0.5 cm in width were cut at the middle of two parallel faces, and then the specimen was split along the notches. The artificial fracture was fully superposed before the strain gauges were embedded and the notches were molded with silicon paste. Finally, a specimen of 150 mm×150 mm×280 mm, with an artificial persistent fracture of 140 mm×280 mm, was prepared, as shown in Fig.5.
Fig.5 Stress applied on specimen
3 Test results
The relationship curves of normal stress and normal deformation are described in Fig.6. It is shown that the normal deformation (being positive while compression) increases as the normal stress increases; in other words, the aperture of the rock fracture decreases when subjected to normal stress. The higher the normal stress is, the lower the increasing rate of the normal deformation is. This indicates that the aperture of the rock fracture tends to achieve a stable value as the normal stress keeps increasing. It is also observed from Fig.6 that plastic deformation appears although it is negligible compared with elastic deformation and the test results are repeatable by circle loading.
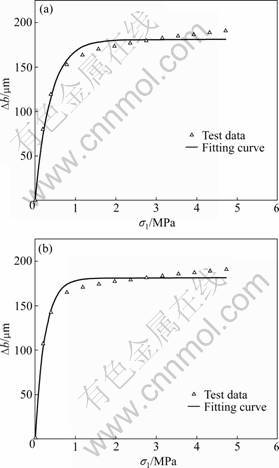
Fig.6 Influence of normal stress on normal deformation of rock fracture: (a) Loading; (b) Unloading.
Figure 7 presents the relationship between the lateral stress and normal deformation. The results indicate that the normal deformation decreases with the lateral stress rising, and the higher the lateral stress is, the greater the growth rate of the normal deformation is. It can be seen from Fig.7 that the relationship between the lateral stress and the normal deformation is affected by the normal stress. When a greater normal stress is applied, the increment of the normal deformation under the same lateral stress is smaller.
Figures 8 and 9 depict the seepage behaviors under the normal stress and the lateral stress, respectively. It is observed from Fig.8 that the hydraulic conductivity descends with the normal stress increasing and tends to achieve a stable value. It is shown in Fig.9 that the hydraulic conductivity increases with the lateral stress rising and that the increasing rate becomes higher.
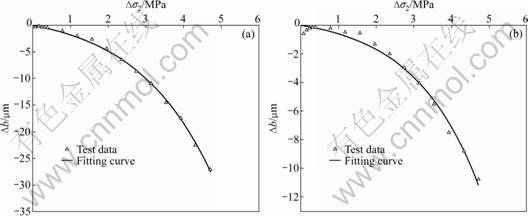
Fig.7 Influence of lateral stress on normal deformation of rock fracture: (a) σ1=0.928 MPa, σ3=0.785 MPa; (b) σ1=1.321 MPa, σ3=0.785 MPa
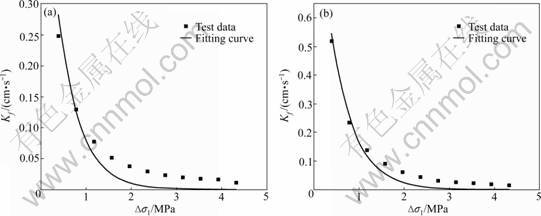
Fig.8 Influence of normal stress on hydraulic conductivity (ΔH=0.5 MPa): (a) 2σ2=σ3=0.785 MPa; (b) σ2=1.178 MPa, σ3=0.785 MPa
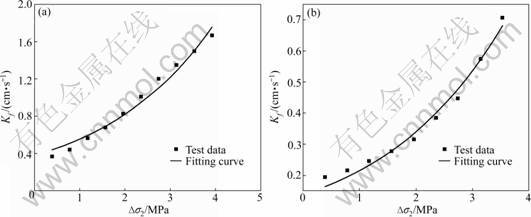
Fig.9 Influence of lateral stress on hydraulic conductivity (ΔH=0.5 MPa): (a) σ1=σ3=0.785 MPa; (b) σ1=1.178 MPa, σ3=0.785 MPa
4 Discussion
The test results show that the normal deformation, as well as the hydraulic conductivity, is affected not only by normal stress but also by lateral stress. SUN and LIN [14] proposed an empirical equation which describes an exponential relationship between the normal deformation and the normal stress, with the following form:
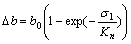 (1)
(1)
where b0 is the maximum closing deformation; Kn is the relevant closing stiffness of the fracture face; Δb is the closing deformation and σ1 is the normal stress.
Figure 6 shows the fitting curves using Eq.(1). It is found that the exponential function can well fit the test data. As presented above, normal deformation increases with the increase of the normal stress but decreases with the growth of the lateral stress. Therefore, it is reasonable to assume that the lateral stress is equivalent to a normal tensile stress (compression being positive) while discussing deformation behavior of a rock fracture. As a result, the normal deformation resulted from the combination of the normal stress and the lateral stress can be expressed as
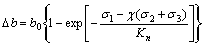 (2)
(2)
where χ is defined as the influencing coefficient of lateral stress on normal deformation, and σ2 and σ3 are the lateral stresses.
Similarly, the test data depicted in Fig.7 are fitted by Eq.(2). It can be seen from Fig.7 that the test data are identical to Eq.(2) and the normal deformation also obeys an exponential relationship with the lateral stress.
According to Barton’s model describing the relationship between the hydraulic aperture and the mechanical aperture [10], the square law can be rewritten as
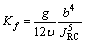 (3)
(3)
where Kf is the hydraulic conductivity; b is the mechanical aperture; g is the gravitational acceleration; 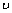 is the viscosity coefficient and JRC is the roughness coefficient.
is the viscosity coefficient and JRC is the roughness coefficient.
Substituting Eq.(2) to Eq.(3) will result in
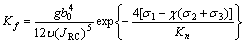 (4)
(4)
Figures 8 and 9 present the test results and the fitting curves by Eq.(4). It is observed from Figs.8 and 9 that the hydraulic conductivity diminishes with increasing the normal stress but increases with rising the lateral stress and the hydraulic conductivity obeys an exponential relationship with the combination of the normal stress and the lateral stresses.
5 Conclusions
1) The true triaxial apparatus composed of three units was successfully designed. This apparatus allows for investigations on deformation/seepage behaviors of a single rock fracture subjected to lateral stress, as well as normal stress.
2) The aperture as well as the hydraulic conductivity descends with the normal stress increasing but increases with the lateral stress rising. The lateral stress can be taken as a normal tensile stress and hence, can be incorporated into Eq.(1) which reveals the deformation behavior of a rock fracture subjected to the normal stress.
3) Further studies on stress, deformation and seepage coupling of rock fractures considering mechanical and geometrical parameters are necessary for a more precise understanding.
References
[1] SNOW D T. Rock fracture spaces, openings and porosities [J]. J Soil Mech, 1968, 94(SM1): 73-91.
[2] LOUIS C. Rock hydrolics [M]. New York: Elsevier Science, 1974.
[3] JONES F O. A laboratory study of the effects of confining pressure on fracture flow and storage capacity in carbonate rocks [J]. J Petrol Technol, 1975, 21(2): 151-159.
[4] GANGI A F. Variation of whole and fractured porous rock permeability with confining pressure [J]. Int J Rock Mech Min Sci, 1978, 15(5): 249-257.
[5] NELSON R A. Fracture permeability in porous reservoirs: Experimental and field approach [D]. Texas: Texas A and M University, 1975.
[6] KRANS R L, FRANKEL A D, ENGELDER T. The permeability of whole and jointed Barre granite [J]. Int J Rock Mech Min Sci and Geomech Abstr, 1979, 16(2): 225-234.
[7] GALE J E. The effects of fracture type on the stress-fracture closure-fracture permeability relationships [C]// Proceedings of the 23rd Symp on Rock Mech. Berkeley: 1982: 290-298.
[8] SU Bao-yu, ZHAN Mei-li, WANG Yuan. Testing study on the characters of seepage and stress coupling of rock fractures [J]. Chinese Journal of Geotechnical Engineering, 1997, 19(4): 73-77. (in Chinese)
[9] LIU Ji-shan. Seepage equation of a single rock fracture under normal stress [J]. Hydrogeology and Engineering Geology, 1987, 14(2): 32-28. (in Chinese)
[10] BARTON N R, BANDIS S C, BAKHTAR K. Strength, deformation and conductivity coupling of rock joints [J]. Int J Rock Mech Min Sci and Geomech Abstr, 1985, 22(3): 121-140.
[11] WALSH J B. A new model for analyzing the effect of fracture on compressibility [J]. J Geophys Resear, 1979, 84(B7): 3532-3536.
[12] GOODMAN R E. Methods of geological engineering in discontinuous rock [M]. New York: West Publishing Company, 1976.
[13] BANDIS S C, LUMSDEN A C, BARTON N R. Fundamentals of rock joint deformation [J]. Int J Rock Mech Min Sci and Geomech Abstr, 1983, 20(6): 249-268.
[14] SUN Guang-zhong, LIN Wen-zhu. Closing deformation law of structural face and elastic constitutive equations of rockmass [J]. Chinese Journal of Geology, 1983, 18(2): 81-88. (in Chinese)
[15] ZHANG Yu-zhu, ZHANG Jin-chang. Experimental study of the seepage flow-stress coupling in fractured rock masses [J]. Chinese Journal of Rock and Soil Mechanics, 1997, 8(4): 59-62. (in Chinese)
[16] ZENG Yi-shan, LU De-tang, ZENG Qing-hong, DONG Hu. Experimental study on coupling of flow-stress within a single fracture [J]. Chinese Journal of Experimental Mechanics, 2005, 20(1): 10-16. (in Chinese)
[17] ZHAO Yang-sheng, YANG Dong, ZHENG Shao-he, HU Yang-qing. Experimental study on seepage characters of rock fractures under triaxial stresses [J]. Science in China (Series E), 1999, 29(1): 82-86. (in Chinese)
(Edited by HE Yun-bin)
Foundation item: Projects(50809069,10872207) supported by the National Natural Science Foundation of China; Project(2009CAD017) supported by Outstanding Youth of Hubei Province, China
Received date: 2011-03-23; Accepted date: 2011-05-23
Corresponding author: LIU Cai-hua, Associate Professor, PhD; Tel: +86-27-87198931; E-mail: chliu@whrsm.ac.cn