文章编号:1004-0609(2016)-08-1711-10
小时滞影响下地下金属矿山人机安全系统动态演化机理辨析
罗周全,左红艳,汪 伟,吴 超
(中南大学 资源与安全工程学院,长沙 410083)
摘 要:为探索地下金属矿山开采过程中人身伤害事故频发的诱发因素,考虑马虎水平对安全水平的小时滞影响性,构建小时滞影响下地下金属矿山开采人机系统马虎性与安全性的非线性动态演化模型。对该演化模型所进行的数学分析和动态演化仿真研究结果较好地验证所构建模型的有效性,而对地下金属矿山开采人机安全非线性动态演化及其趋势定性分析不但揭示了4个动态区域内马虎水平与安全水平的相互作用演化模式,还可为地下金属矿山开采人机安全系统的安全评价与控制提供依据。
关键词:地下金属矿山;小时滞;人机安全系统;动态演化机理
中图分类号:X936 文献标志码:A
对于地下金属矿山开采安全而言,采用静态安全评价方法一般只能说明其安全性指标处于某种范围,并不能真正揭示地下金属矿山开采安全动态演化过程的动态演化规律,容易导致实际过程中静态安全评价、安全趋势以及事故率不吻合的现象发生[1]。而动态演化理论则是关于基于非建构性、非人为设计性原理的一种以演进理性为基础的非线性动态非均衡的演化过程的理论[2-3]。
我国地下金属矿山开采安全生产形势远滞后于现代化经济建设的步伐,地下金属矿山开采过程中人员伤害事故频发与安全生产问题日益突出[4-5]。因此,如何有效解决地下金属矿山开采的伤害事故问题,是广大金属矿山安全工作者及工程技术人员刻不容缓的课题[6]。如何有效探索地下金属矿山开采过程中人身伤害事故频发的诱发因素究竟是机械设备问题还是人自身的问题显得十分紧迫,而人机安全工程学原理则为从系统的观点出发对地下金属矿山开采过程中人身伤害事故频发现象重新认识[7-8],并有效地克服片面性[9],进而为提出可行的安全对策提供很好的思路[10]。
众所周知,地下金属矿山开采过程中马虎性对安全性的作用或影响是有时滞作用的,即马虎性的变化需在一定的时间内才能在安全性上显现出来。因此,很有必要考虑不同时滞大小对地下金属矿山开采人机安全动态演化的影响[11-12],并利用时滞微分方程理 论[13-14]建立不同时滞大小时滞影响下地下金属矿山开采人机安全动态演化模型。为不失一般性,本文作者将先研究小时滞对地下金属矿山开采人机安全动态演化的影响,辨析小时滞影响下地下金属矿山开采安全动态演化特征,从而为有效揭示小时滞影响下地下金属矿山开采安全动态演化机理的奠定坚实的理论基础。
1 地下金属矿山开采安全人机系统分析
1.1 地下金属矿山开采过程人机系统认识
近20多年来,地下金属矿山开采装备在很大程度上实现了无轨化和液压化,并有向大型化、自动化甚至智能化方向发展的趋势[15]。在地下金属矿山开采过程中,人和开采装备组成的人机系统整体水平的提升将是提高地下金属矿山开采产量、降低生产成本、改善开采安全和生产条件切实可行的手段。一般而言,地下金属矿山开采人机系统主要包括人-钻机系统、人-管道铺设装备系统、人-铁道铺设装备系统、人-铲运机系统、人-液压凿岩台车系统、人-爆破系统、人-支护系统、人-松石装备系统和人-装药台车系统等,这些人机系统作业又可分解为检查作业、启动停车作业、维修保养作业、行驶作业和开采作业等,如图1所示。
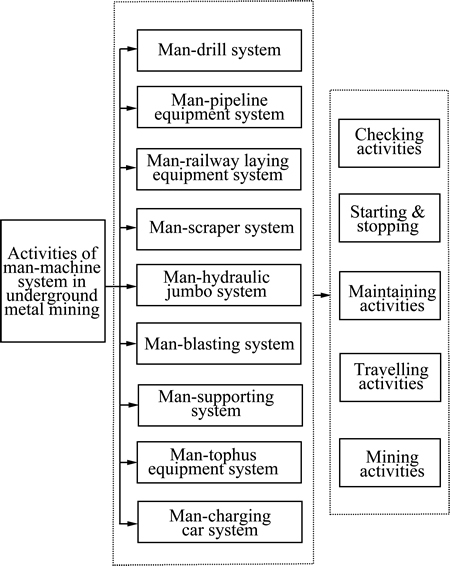
图1 金属矿资源地下开采人机环境系统
Fig. 1 Human-machine environment system of underground metal resources mining
地下金属矿山开采人机系统所组成的两个子系统(即人子系统和机子系统)有各自的特点。因此,对地下金属矿山开采安全事故的分析不能简单化,应从开采人机系统的角度出发采取有效的安生对策。当机子系统被操作时,人子系统的可靠度为R1,机子系统的可靠度为R2,则地下金属矿山开采人机系统的可靠度Rs可表示为
Rs=R1R2 (1)
1.2 地下金属矿山开采安全事故发生的人因分析
1.2.1 人机环境系统信息通道单向性导致人的失误
地下金属矿山开采人机系统的信息通道是单向的,即由人子系统向机子系统下达指令而机子系统无信息反馈[16]。当机子系统出现故障时,地下金属矿山开采人机系统所构成的网络的单回路结构将使地下金属矿山开采人子系统处于不利状况:1) 信息处理速度大大降低;2) 同时判断处理两个以上故障信息的能力丧失;3) 使人子系统忙乱,不能处理紧急情况下的多种判断;4) 当遭遇突然出现的异常情况和险情等异常性时,地下金属矿山开采人子系统中的人脑系统“软件”很自然地陷入“呆傻”状况。
1.2.2 人机环境系统中人的警觉性丧失
地下金属矿山开采人子系统在操作过程中,其思维、判断及信息处理都必须与特定的地下金属矿山开采人机环境条件相匹配。所谓人的警觉性丧失是指人子系统由于忘记自己的地下金属矿山开采特定环境。对于地下金属矿山开采生产现场而言,在不经治理的噪音以及湿热环境等因素影响下,操作人员每天连续工作4~5 h,在生产中难免会产生单调感,极易产生心理和体力的疲劳,使大脑意识水平下降,操作中注意力涣散,从而导致误操作时常发生。对地下金属矿山开采人子系统的行为分析可以得知,由于地下金属矿山开采机子系统连续而单调的噪音及几乎频率相同的振动,使人子系统产生心理和生理部分的同步效应。一旦机子系统停止工作,人子系统心理会产生失平衡,将使人子系统的警觉性丧失,从而最终将导致人子系统失误。
2 小时滞影响的地下金属矿山开采安全动态演化模型
2.1 小时滞影响的地下金属矿山开采人机安全动态演化模型建立
当地下金属矿山开采人机系统中的人员处于高安全性时,往往容易产生松懈感,从而致使马虎性上升,最终导致地下金属矿山开采人机系统安全性降低;相反,当地下金属矿山开采人机系统中的人员处于低安全性时,绷紧的神经反而会致使马虎性降低。也就是说,地下金属矿山开采人机系统中的安全性与马虎性是相互交织、相互作用的非线性相关的两个变量。
为建立地下金属矿山开采安全动态演化模型,不妨作如下假设。
1) 基于人因安全理论[13],设τ时刻地下金属矿山开采人机系统的安全水平值和马虎水平值分别为x(τ)和y(τ),且x(τ)和y(τ)还满足以下特性:① x(τ)越大,则表明地下金属矿山开采人机系统安全水平越高;x(τ)越小,则表明地下金属矿山开采人机系统安全水平越低;② y(τ)越大,地下金属矿山开采人机系统的警觉性越低,思想松懈、行为马虎程度越高;y(τ)越小,地下金属矿山开采人机系统的警觉性越高,思想松懈、行为马虎程度越低。
2) 设地下金属矿山开采人机系统的安全水平和马虎水平的内禀增长率分别为a1(其中a1>0)和b1(其中b1>0)。
3) 地下金属矿山开采环境对安全水平和马虎水平的阈值分别为M(且M>0)和m(且m>0),且有m<M。
考虑到马虎水平对安全水平的影响具有时滞τ0,故设τ时刻时马虎水平y(τ)对安全水平演化速度dx(τ)/dτ的影响为-a2y(τ-τ0),同时,在τ时刻,地下金属矿山开采安全性状态演化速度dx(τ)/dτ还受到安全水平x(τ)以及安全水平变化趋势[1-x(τ)/M]的耦合作用,则地下金属矿山开采安全性状态演化速度dx(τ)/dτ可表示为
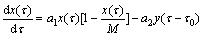 (2)
(2)
式中:a2为马虎性对安全性影响系数,且a2>0。
由式(2)可看出,安全水平内禀增长率a1可有效描述安全水平增长速度与即时安全水平及安全水平变化趋势之间的线性关系,a1越大,则说明即时安全水平及安全水平变化趋势对安全水平增长速度的耦合影响作用越大;而马虎性对安全性影响系数a2可较好地描述马虎性与安全水平增长速度之间的线性关系,a2越大,则说明马虎性对安全性影响作用越大。
此外,设τ时刻时马虎水平y(τ)对马虎水平演化速度dy(τ)/dτ的影响为-b2y(τ),而τ时刻时安全水平x(τ)对马虎水平演化速度dy(τ)/dτ的影响为b1[m-x(τ)]x(τ),则地下金属矿山开采马虎性状态演化速度dy(τ)/dτ可表示为
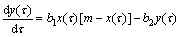 (3)
(3)
式中:b2为抵制系数,且b2>0。
式(3)表明,马虎水平内禀增长率b1可有效描述马虎性的增长速度与存在的马虎水平阈值m和安全水平x(τ)的差值以及安全水平x(τ)的耦合作用之间的线性关联,当x(τ)<m,意味着地下金属矿山开采安全性不足,此时马虎水平随安全水平x(τ)的增长而增强;当x(τ)>m时,意味着地下金属矿山开采安全性得到充分加强,此时,马虎水平随安全水平x(τ)的增长而降低。而模型中马虎性抵制系数b2可对地下金属矿山开采人员马虎性的增长速度与警觉水平之间所具有的负线性关系进行有效描述,即马虎性越高,其马虎水平增长越缓慢。
显然,式(2)和(3)所示的数学模型能对地下金属矿山开采过程的安全性和马虎性之间的动态演化关系以及动态演化规律进行有效的描述。
令u(τ)=x(τ)/M,v(τ)=y(τ)/M,a2t=τ,则式(2)和(3)变形可得
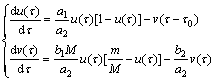 (4)
(4)
令a=a1/a2,b=b2/a2,c=b1·M/a2,d=m/M,并将τ改写为t,将τ0改为t0,令u(τ)=u(t),v(τ)=v(t),则式(4)所示的常微分方程组可变形为
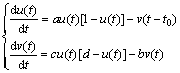 (5)
(5)
显然,式(4)所示的常微分方程组和式(2)与式(3)所示的常微分方程的相图拓扑同胚[17]。
2.2 小时滞地下金属矿山开采安全动态演化模型数学分析
假设(a1+b2)2/(4a2b1)<m<M(即(a+b)2/(4c)<d<1)成立,对地下金属矿山开采安全动态演化模型进行数学分析。
定理1 若常微分方程组(5)中a≤b,则常微分方程组(5)无闭轨,即无周期解。
证明:令u(t)=u,v(t)=v,取Dulac函数B(u, v)= e(ku+lv),考虑到τ0较小,则
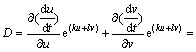
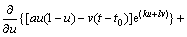
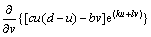 (6)
(6)
将v(t-t0)在点t处按泰勒展开式展开,有
v(t-t0)=v(t)-t0dv(t)/dt。 (7)
将式(7)代入式(6)可得
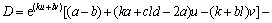
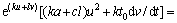
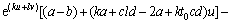
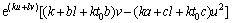 (8)
(8)
令ka+cld-2a+kt0cd=0,k+bl+kt0b=0,联立求解可得k=-2ab/(cd-ab),l=2a(t0b+1)/(cd-ab)。
于是
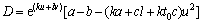 (9)
(9)
因(a1+b2)2/(4a2b1)<m<M(即(a+b)2/(4c)<d<1),故得cd>ab。
考虑ak+cl+kt0c=2a(c-ab)/(cd-ab)>2a(cd-ab)/ (cd-ab)>0,故当a≤b时,则有D≤0,等号仅在a=b和u=0时出现,由Dulac准则可知,常微分方程组(5)无闭轨,即无周期解。因此,定理1证毕。
定理2 常微分方程组(5)有两个有限奇点(0,0)和(u0,v0)(其中u0=(ab-cd)/(ab-c),v0=cu0(d-u0)/b;(u0,v0)在第一象限内,是鞍点;(0,0)是稳定粗焦点(a<b-t0cd时)。
将式(7)代入常微分方程组(5),经整理后可得
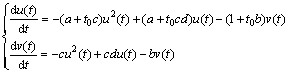 (10)
(10)
令du(t)/dt=0,dv(t)/dt=0,并为简便起见省去变量t,记u(t)=u,v(t)= v,则有
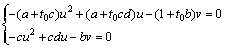 (11)
(11)
解式(11)可得u0=(ab-cd)/(ab-c),v0=cu0(d-u0)/b)。由于cd>ab,d<1,于是c>ab,显然有u0=(ab-cd)/(ab-c)>0。
(ab-cd)/(ab-c)-d=(cd-ab)/(c-ab)-d=ab(d-1)/(c-ab)<0,则有u0=(ab-cd)/(ab-c)<d。因此,显然有v0=cu0(d-u0)/b>0,即(u0,v0)在第一象限内。
令ξ=u-u0,η=v-v0,则式(10)变成
 (12)
(12)
式(12)的线性近似系统的特征方程为
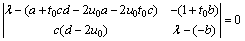 (13)
(13)
对式(13)化简后可得
λ2+[b-(a+t0cd-2u0a-2u0t0c)]λ-b(a+t0cd-2u0a-2u0t0c)+c(1+bt0)(d-2u0)=0 (14)
其中常数项-b(a+t0cd-2u0a-2u0t0c)+c(1+bt0) (d-2u0)=-ab+2u0ab+cd-2u0c=cd-ab+2u0(ab–c)=cd-ab+2[(ab-cd)/(ab-c)](ab–c)=cd-ab+2(ab-cd)=ab-cd<0。
式(12)的线性近似系统的特征方程的特征根是异号实数,且(u0,v0)为第一象限内的鞍点。
对于奇点(0,0),式(12)的线性近似系统的特征方程为
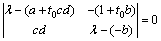 (15)
(15)
对式(15)简化后可得
λ2+(b-a-t0cd)λ+cd-ab=0 (16)
则式(16)的特征根为
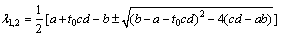 (17)
(17)
由于(a+b)2/(4c)<d<1,cd>ab,则(b-a-t0cd)2– 4(cd-ab)<(b-a)2-4(cd–ab)=(b+a)2-4ab–4(cd–ab)= (b+a)2-4cd<0。因此,特征根λ1、λ2是实部为(a+t0cd-b)/2<0的共轭复数,故a<b-t0cd时,(0,0)为稳定粗焦点。
定理3 对于常微分方程组(5),1) 当a=b-t0cd时,(0,0)是稳定的一阶细焦点;2) 当a>b-t0cd时,(0,0)是不稳定粗焦点;3) 当0<a+t0cd-b<<1时,(0,0)外围存在唯一极限环,它是单重稳定环;4) 当a+t0cd-b>(a+t0c)(ab-cd)/(ab-c)时,(0,0)外围不存在极限环。
证明:用x代替u(t),用y代替v(t),常微分方程组(10)可变行为
 (18)
(18)
令x=(1+t0b)S,T=bx/(1+t0b)-y,则常微分方程组(18)可变行为
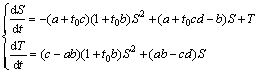 (19)
(19)
令Z=(ab-cd)T,则常微分方程组(19)可变行为
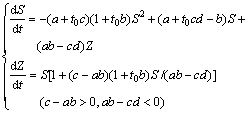 (20)
(20)
求(dZ/dt)与(dS/dt)的比值,有
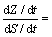
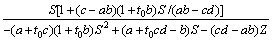 (21)
(21)
式(21)两边同时乘以(ab-cd)1/2,则可得
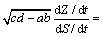
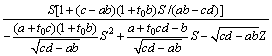 (22)
(22)
令W=(cd-ab)1/2Z,则由式(22)可得
 (23)
(23)
令S← -S,W← -W,则:
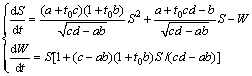 (24)
(24)
Δ=(a+t0cd-b)/(cd-ab)1/2,L=(a+t0c)(1+t0b)/(cd-ab)1/2,A=(c-ab)(1+t0b)/(cd-ab),式(24)可改写为
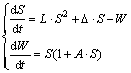 (25)
(25)
1) 当a=b-t0cd时,Δ=0,此时式(25)为式(26)所示常微分方程组的特例。在式(25)中,a20=L,b20=A,a11=b11=a02=b02=0。第一阶细焦点量G1=(a20+a02)· (a11+2b02)-(b20+b02)(b11+2a20)= -2LA<0,可见(0,0)是稳定的一阶细焦点。
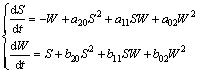 (26)
(26)
2) 当a>b-t0cd时,式(25)的线性近似系统的特征方程为
λ2-Δλ+1=0 (27)
已知a>b-t0cd,cd>ab,则有Δ=(a+t0cd-b)/ (cd-ab)1/2>0,特征根的实部Δ/2>0的共轭复数,故(0,0)是不稳定粗焦点。
3) 由Hopf分叉理论可知,当0<a+t0cd-b<<1时,则(0,0)外围至少存在1个稳定的极限环。
式(25)为式(28)所示的叶彦谦意义下的第2类二次微分系统的特例(I=K=0)。当Δ≤0或Δ≥L/A(即a+t0cd-b>(a+t0c)(ab-cd)/(ab-c)时),常微分方程组(25)无极限环,而当0<Δ<L/A时,则至多存在1个极限环,且若存在,必为(0,0)外围的单重稳定极限环。故当0<a+t0cd-b<<1时,式(25)在(0,0)外围存在唯一的单重稳定极限环。
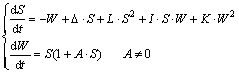 (28)
(28)
2.3 小时滞地下金属矿山开采人机安全非线性动态演化分析
根据建立的地下金属矿山开采人机安全非线性动态演化数学模型,通过相图分析,能够对马虎性与安全性的相互作用演化模式进行定性分析,因而,可以为安全评价与控制提供依据。根据定理1~3,可绘出地下金属矿山开采人机安全非线性动态演化相图(见图2~4)。
在图2~4中所围成的EFGH区域中,曲边梯形DBGHD是地下金属矿山开采人机安全系统发展区域,阴影部分区域是地下金属矿山开采人机安全系统动荡区域,其余部分为地下金属矿山开采人机安全系统崩溃区域。其中曲线AC和BD相交于鞍点E2(u0,v0),将EFGH区域划分为地下金属矿山开采人机安全系统安全保障区域Ⅰ、地下金属矿山开采人机安全系统安全恶化区域Ⅱ、地下金属矿山开采人机安全系统安全渐进稳定区域Ⅲ和地下金属矿山开采人机安全系统安全能力提升区域Ⅳ等4个动态区域。
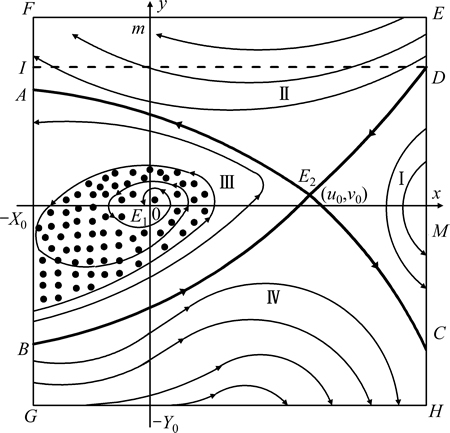
图2 无闭轨情况地下金属矿山开采人机安全非线性动态演化过程
Fig. 2 Human-machine safety nonlinear dynamic evolution process of underground metal mining at situation of unclosed rail
1) 无闭轨情况
由地下金属矿山开采人机安全动态演化模型可知,a=a1/a2,b=b2/a2。当a≤b-t0cd时,意味着a1≤b2-b1mτ0/a2,即地下金属矿山开采人机安全系统的马虎水平内禀增长率b1、马虎水平阈值m和等效时滞τ0/a2的乘积与安全水平内禀增长率a1之和小于马虎性抵制系数b2,此时地下金属矿山开采人机安全动态演化模型具有2个奇点E1(0,0)、E2(u0,v0)(其中E2(u0,v0)为鞍点,E1(0,0)为稳定焦点),且无闭轨,如图3所示。
图2表明:
a) 在区域Ⅰ内,由于马虎性程度较低,地下金属矿山开采人机安全系统安全水平相当稳定,趋于极限,具有非常好的安全发展趋势。b) 在区域Ⅱ内,由于马虎性程度较高,地下金属矿山开采人机安全系统安全水平将随时间的进行而不断恶化,并最终可能导致地下金属矿山开采人机安全系统崩溃。例如,如果地下金属矿山开采人机安全系统安全水平状态处于地下金属矿山开采人机安全系统崩溃区域,即使当初安全水平在阈值M附近,随着时间的推移,在有限时间内,地下金属矿山开采人机安全系统安全水平趋于崩溃线x=-X0。c) 在区域Ⅲ内,地下金属矿山开采人机安全系统处于振荡状态,马虎性与安全水平的振荡幅度不断减弱,最终趋于马虎与警惕、安全与危险的均衡点E1(0,0)。d) 在区域Ⅳ内,随着时间的推移,地下金属矿山开采人机安全系统安全提升能力得到不断改善,并最终可趋于地下金属矿山开采人机安全系统安全水平阈值M。
2) 存在唯一极限环情况
由地下金属矿山开采人机安全动态演化模型可知,当a>b-t0cd时,意味着a1>b2-b1mτ0/a2,即地下金属矿山开采人机安全系统的马虎水平内禀增长率b1、马虎水平阈值m和等效时滞τ0/a2的乘积与安全水平内禀增长率a1之和大于马虎性抵制系数b2,此时地下金属矿山开采人机安全动态演化模型的奇点E1(0,0)为不稳定粗焦点;且当0<a+t0cd-b<<1时(即0<a1+b1mτ0/a2-b2<<1),意味着马虎水平内禀增长率b1、马虎水平阈值m和等效时滞τ0/a2的乘积与安全水平内禀增长率a1之和略大于马虎性抵制系数b2,奇点E1(0,0)外围存在唯一的单重稳定极限环,如图3所示。
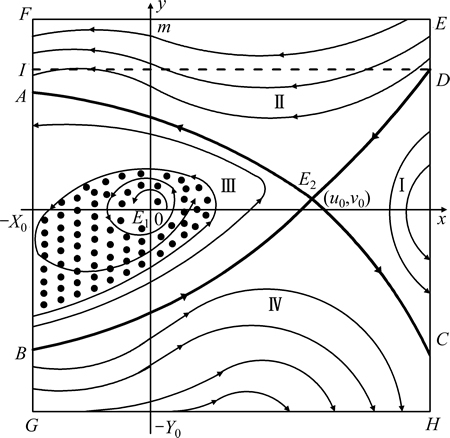
图3 存在唯一极限环情况地下金属矿山开采人机安全非线性动态演化过程
Fig. 3 Human-machine safety nonlinear dynamic evolution process of underground metal mining at situation of unique limit cycle
比较图2和3可知,图2和3中区域Ⅰ、区域Ⅱ和区域Ⅳ的演化模式基本相同,而区域Ⅲ却表现出不同的演化状态。其主要原因为:当马虎水平内禀增长率b1、马虎水平阈值m和等效时滞τ0/a2的乘积与安全水平内禀增长率a1之和略大于马虎性抵制系数b2时,地下金属矿山开采人机安全系统的安全水平内禀增长率受到较小程度的抑制,而马虎水平则得到较小程度的增强,从而导致此区域内安全水平和马虎水平较小程度的聚集性振荡,如在奇点E1(0,0)附近先螺旋式振荡,并趋于单重稳定极限环;当马虎水平内禀增长率b1、马虎水平阈值m和等效时滞τ0/a2的乘积与安全水平内禀增长率a1之和大于马虎性抵制系数b2时,地下金属矿山开采人机安全系统的安全水平内禀增长率受到一定的抑制,而马虎水平则得到一定的增强,从而导致此区域内安全水平和马虎水平在单重稳定极限环外不断进行聚集性拟周期或者聚集性周期振荡。
3) 无极限环情况
由地下金属矿山开采人机安全非线性动态演化模型可知,当a+t0cd-b>(a+t0c)(ab-cd)/(ab-c)时, a1+b1mτ0/a2-b2>(a1/a2+b1Mτ0/a22)(a1b2-a2b1m)/(a1b2- a2b1m)。即地下金属矿山开采人机安全系统的马虎水平内禀增长率b1、马虎水平阈值m和等效时滞τ0/a2的乘积与安全水平内禀增长率a1之和明显大于马虎性抵制系数b2,此时地下金属矿山开采人机安全动态演化模型存在一个不稳定焦点E1(0,0),且不存在极限环,如图4所示。
与图2、3比较可知,图4和图2、3中区域Ⅰ、区域Ⅱ和区域Ⅳ的演化模式仍然基本相同,仅是区域Ⅲ表现出不同的演化状态。其主要原因为:当地下金属矿山开采人机安全系统的马虎水平内禀增长率b1、马虎水平阈值m和等效时滞τ0/a2的乘积与安全水平内禀增长率a1之和明显大于马虎性抵制系数b2时,地下金属矿山开采人机安全系统的安全水平内禀增长率受到很大程度的抑制,而马虎水平得到很大程度的增强,从而导致此区域内安全水平和马虎水平较小程度的发散性振荡(如奇点E1(0, 0)为不稳定焦点),随着时间推移,经过一定的发散性振荡后,地下金属矿山开采人机安全系统的安全水平将最终趋于崩溃。
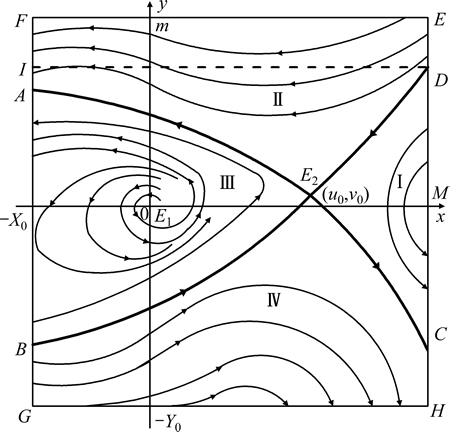
图4 无极限环情况地下金属矿山开采人机安全非线性动态演化过程
Fig. 4 Human-machine safety nonlinear dynamic evolution process of underground metal mining at situation of unlimited cycle
2.4 地下金属矿山开采人机安全非线性动态演化趋势定性分析
如图5所示,通过地下金属矿山开采人机安全非线性动态演化相图也可定性分析开采人机安全系统人机安全非线性动态演化趋势。
1) 安全水平取定值
当地下金属矿山开采人机安全系统的安全水平为x=u1时,图5中直线x=u1在相图上与AC和BD有两个交点E和F,意味着对应的安全性区域有3种可能,即EF代表安全振荡区,FP1代表安全恶化区,EQ1代表安全能力提升区。当直线x=u1的右平移时,安全振荡区减小,安全能力提升区和安全恶化区均增加,当直线x=u1的左平移时,安全振荡区增大,安全能力提升区和安全恶化区均减小。由于直线x=u2通过AC和BD的交点E2(u0,v0),其对应的安全性区域只有2种可能,即E2P1代表安全恶化区,E2Q1代表安全能力提升区。
地下金属矿山开采人机安全系统安全状态不在地下金属矿山开采人机安全系统发展区域内,若马虎水平的恶化程度尚在DR线之下,则只需维持其不再增加,而全力提高操作水平和快速应变能力,即可将安全状态回归地下金属矿山开采人机安全系统发展区域内。
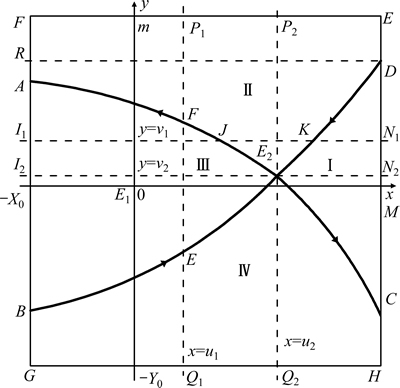
图5 地下金属矿山开采人机安全非线性动态演化趋势定性分析
Fig. 5 Qualitative analysis on nonlinear dynamic evolution trend of human-machine safety in underground metal mining
2) 马虎水平取定值
当地下金属矿山开采人机安全系统的马虎水平为y=v1时,图5中直线y=v1在相图上与AC和BD有两个交点J和K,意味着对应的安全性区域有3种可能,即I1J代表安全振荡区,JK代表安全恶化区,KN1代表安全区。随着直线y=v1的上下平移,其相应的区域随之变化。当马虎水平程度降低时,直线y=v1平移下移,安全恶化区变小,安全振荡区和安全区均变大,安全性恶化的可能性减小。由于直线y=v2通过AC和BD的交点E2(u0, v0),其对应的安全性区域只有2种可能,即E2I2代表安全振荡区,E2N2代表安全区。
地下金属矿山开采人机安全系统安全状态不在地下金属矿山开采人机安全系统发展区域内,则只需维持操作水平和快速应变能力不再增加,而全力克服马虎性,提高警惕性,确保安全状态回归开采人机安全系统发展区域内。
3 地下金属矿山开采安全动态演化仿真研究
不同的地下金属矿山开采人机安全系统对应不同的参数组{a1, a2, b1, b2, m, M},为具体地研究某地下金属矿山开采人机安全系统的非线性动态演化状态(x(τ)=u, y(τ)), 首先必须确定该地下金属矿山开采人机安全系统对应不同的参数组{a1, a2, b1, b2, m, M}。
设x1(τ)为人-钻机系统安全水平;x2(τ)为人-管道铺设装备系统安全水平;x3(τ)为人-铁道铺设装备系统安全水平;x4(τ)为人-铲运机系统安全水平;x5(τ)为人-液压凿岩台车系统安全水平;x6(τ)为人-爆破系统安全水平;x7(τ)为人-支护系统安全水平;x8(τ)为人-松石装备系统安全水平;x9(τ)为人-装药台车系统安全水平,则
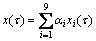 (29)
(29)
式中:αi为安全水平权重系数。
同理,设y1(τ)为人-钻机系统马虎水平;y2(τ)为人-管道铺设装备系统马虎水平;y3(τ)为人-铁道铺设装备系统马虎水平;y4(τ)为人-铲运机系统马虎水平;y5(τ)为人-液压凿岩台车系统马虎水平;y6(τ)为人-爆破系统马虎水平;y7(τ)为人-支护系统马虎水平;y8(τ)为人-松石装备系统马虎水平;y9(τ)为人-装药台车系统马虎水平,则
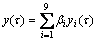 (30)
(30)
式中:βi为安全水平权重系数。
以时滞为时间间隔,可采用问卷调查或专家评价等方法确定历史上的安全水平值xi(τ)和yi(τ),并采用层次分析方法[18]确定安全水平权重系数αi和βi。
以时滞为时间间隔,对式(2)和(3)进行差分,可得
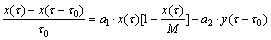 (31)
(31)
 (32)
(32)
将得到的各个历史水平值(x(τ), y(τ))代入式(31)和式(32),即可求得该地下金属矿山开采人机安全系统对应不同的参数组{a1,a2,b1,b2,m,M}。
按以上方法求得某地下金属矿山开采人机安全系统对应不同的参数组{a1,a2,b1,b2,m,M}={0.20,0.20,0.7,0.4,0.80,1.00},可得a=a1/a2=1.0,b=b2/a2=2.0,c=b1M/a2=3.5,d=m/M=0.8。显然有2cd>c+ab和cd>ab成立,则某地下金属矿山开采 安全动态演化模型平衡点的坐标为El=(0, 0), E2=( 0.5333, 0.2489)。
由b=2.0>a=1.0,可知地下金属矿山开采人机安全系统的安全水平内禀增长率a1小于马虎性抵制系数b2,故根据定理3可知平衡点稳定状态存在两种可能:1) 当t0=(b-a)/cd=1/2.8,有τ0=t0/a2=1.7857 s时,此时(0, 0)是稳定的一阶细焦点;2) 当a+t0cd-b>(a+t0c)(ab-cd)/(ab-c)时(即τ0>1.9167s时),(0,0)外围不存在极限环;3) 当0<a+t0cd-b<<1(即1.7857 s=t0/a2<τ0<<3.5714 s)时,由于1.7857<<3.5714不成立,故(0, 0)外围不存在唯一极限环;4) 当1.9167 s>τ0>t0/a2=1.7857 s时,(0, 0)是不稳定粗焦点。
4 结论
1) 考虑马虎水平对安全水平的影响具有时滞τ0效果,构建了小时滞影响下地下金属矿山开采人机系统马虎性与安全性的非线性动态演化模型,并对该演化模型进行了有效的数学分析和动态演化仿真。研究结果较好地验证了所构建的小时滞影响下地下金属矿山开采人机系统非线性动态演化模型的有效性。
2) 对小时滞影响下地下金属矿山开采人机安全非线性动态演化及其趋势定性进行了分析,揭示了小时滞影响下安全保障区域Ⅰ、安全恶化区域Ⅱ、安全渐进稳定区域Ⅲ和安全能力提升区域Ⅳ等4个动态区域内马虎水平与安全水平的相互作用演化模式,可为小时滞影响下地下金属矿山开采人机安全系统的安全评价与控制提供依据。
REFERENCES
[1] 左红艳, 罗周全. 地下金属矿山开采过程人机环境安全机理辨析与灾害智能预测[M]. 北京: 中国水利水电出版社, 2014.
ZUO Hong-yan, LUO Zhou-quan. Human machine environment safety mechanism analysis and disaster intelligent prediction in the process of underground metal mine[M]. Beijing: China Water Conservancy and Hydropower Publishing House, 2014.
[2] ZUO Hong-yan, LUO Zhou-quan, GUAN Jia-lin, WANG Yi-wei. Identification on rock and soil parameters for vibration drilling rock in metal mine based on fuzzy least square support vector machine[J]. Journal of Central South University, 2014, 21(3): 1085-1090.
[3] 于 明, 孙林岩, 崔 凯. 人机系统警觉性与安全性的非线性演化研究[J]. 工业工程与管理, 2008, 13(5): 54-57.
YU Ming, SUN Lin-yan, CUI Kai. Study on nonlinear dynamic evolutionary patterns of vigilance and safety in human-machine system[J]. Industrial Engineering and Management, 2008, 13(5): 54-57.
[4] 尹土兵, 王 品, 张鸣鲁. 基于AHP及模糊综合评判的地下金属矿山安全分析与评价[J]. 黄金科学技术, 2015, 23(3): 60-66.
YIN Tu-bing,WANG Pin,ZHANG Ming-lu. Analysis and evaluation of safety in underground metal mine based on AHP and fuzzy evaluation method[J]. Gold Science and Technology, 2015, 23(3): 60-66.
[5] 张 舒, 史秀志, 古德生, 黄刚海. 基于ISM和AHP以及模糊评判的矿山安全管理能力分析与评价[J]. 中南大学学报(自然科学版), 2011, 42(8): 2406-2416.
ZHANG Shu, SHI Xiu-zhi, GU De-sheng, HUANG Gang-hai. Analysis and evaluation of safety management capability in mine based on ISM and AHP and fuzzy evaluation method[J]. Journal of Central South University (Science and Technology), 2011, 42(8): 2406-2416.
[6] 史秀志, 保 瑞, 张 舒, 赵艳艳. 地下金属矿山安全标准化系统信息平台的构建与应用[J]. 安全与环境学报, 2011, 11(1): 184-188.
SHI Xiu-zhi, BAO Rui, ZHANG Shu, ZHAO Yan-yan. Construction and platform based on application of the information safety standardization system for the underground metal mine[J]. Journal of Safety and Environment, 2011, 11(1): 184-188.
[7] ZUO Hong-yan, LUO Zhou-quan, WU Chao. Classification identification of acoustic emission signals from underground metal mine rock by ICIMF classifier[J]. Mathematical Problems in Engineering, 2014, 2014(4): 1-4.
[8] ZUO Hong-yan, LUO Zhou-quan, WU Chao. Research on classification effectiveness of the novel Mamdani fuzzy classifier[J]. Applied Mechanics and Materials, 2014, 511/512: 871-874.
[9] 左红艳, 罗周全, 王益伟, 王爽英. 基于模糊自适应变权重算法的采场冒顶函数链神经网络预报[J]. 中国有色金属学报, 2011, 21(4): 894-900.
ZUO Hong-yan, LUO Zhou-quan, WANG Yi-wei, WANG Shuang-ying. Prediction of functional link neural network of roof caving based on fuzzy adaptive variable weight method[J]. The Chinese Journal of Nonferrous Metals, 2011, 21(4): 894-900.
[10] HU Yu-xi, LI Xi-bing. Bayes discriminant analysis method to identify risky of complicated goaf in mines and its application[J]. Transactions of Nonferrous Metals Society of China, 2012, 22(2): 425-431.
[11] HAN Mao-an. Bifurcations of periodic solutions of delay differential equations[J]. Journal of Differential Equations, 2003, 189(2): 396-411.
[12] WALTHER H O. A periodic solution of a differential equation with state-dependent delay[J]. Journal of Differential Equations, 2008, 244(8): 1910-1945.
[13] WALTHER H O. The solution manifold and C1-smoothness for differential equations with state-dependent delay[J]. Journal of Differential Equations, 2003, 195(1): 46-65.
[14] MALLET-PARET J, NUSSBAUM R D. Superstability and rigorous asymptotics in singularly perturbed state-dependent delay-differential equations[J]. Journal of Differential Equations, 2011, 250(11): 4037-4084.
[15] 史秀志, 陆 广, 张 舒. 金属矿山地下开采系统的风险管理研究[J]. 安全与环境工程, 2008, 15(1): 108-111.
SHI Xiu-zhi, LU Guang, ZHANG Shu. Study of risk management in underground mining system of metal mines[J]. Safety and Environmental Engineering, 2008, 15(1): 108-111.
[16] 王宝国, 王新全, 霍 然, 刘淑艳. 安全人机工程学[M]. 北京: 机械工业出版社, 2007.
WANG Bao-guo, WANG Xin-quan, HUO Ran, LIU Shu-yan. Safety Ergonomics[M]. Beijing: China Machine Press, 2007.
[17] 王树禾. 微分方程模型与混沌[M]. 合肥: 中国科技大学出版社, 1999.
WANG Shu-he. Differential equation model and chaos[M]. Hefei: University of Science and Technology of China Press, 1999.
[18] 王爽英, 吴 超, 左红艳. 中小型煤矿生产安全模糊层次分析评价模型及其应用[J]. 中南大学学报(自然科学版), 2010, 41(5): 1914-1918.
WANG Shuang-ying, WU Chao, ZUO Hong-Yan. Fuzzy analytic hierarchy process assessment model of safety production for small and medium coal mines and its application[J]. Journal of Central South University (Science and Technology), 2010, 41(5): 1914-1918.
Dynamic evolution mechanism analysis of human-machine safety system with little time delay in underground metal mining
LUO Zhou-quan, ZUO Hong-yan, WANG Wei, WU Chao
(School of Resource and Safety Engineering, Central South University, Changsha 410083, China)
Abstract: Considering the little time delay impact of careless level on the safety level, a nonlinear dynamic evolution model about the careless and safety of the human-machine system with little time delay was built to explore the predisposing factors of frequent personal injury accident in the underground metal mining. And the validity of constructed model was well verified by the simulation results studied in the mathematical analysis and dynamic evolution of the dynamic evolution model. In addition, the qualitative analysis on nonlinear dynamic evolution and trend of safety with little time delay in the underground metal mining not only reveals the interaction evolution model of careless level and safety level in the four dynamic regions, but also provides basis for the safety evaluation and control of the human-machine safety system in the underground metal mining.
Key words: underground metal mining; little time delay; human-machine safety system; dynamic evolution mechanism
Foundation item: Project(2012BAK09B02-05) supported by the National “Twelfth Five-year” Science & Technology Support Plan of China; Project(51274250) supported by the National Natural Science Foundation of China
Received date: 2016-05-10; Accepted date: 2016-06-22
Corresponding author: ZUO Hong-yan; Tel: +86-15084931748; E-mail: zuohongyan18@126.com
(编辑 李艳红)
基金项目:国家“十二五”科技支撑计划资助项目(2012BAK09B02-05);国家自然科学基金资助项目(51274250)
收稿日期:2016-05-10;修订日期:2016-06-22
通信作者:左红艳,讲师,博士;电话:15084931748;E-mail: zuohongyan18@126.com