J. Cent. South Univ. (2012) 19: 816-823
DOI: 10.1007/s11771-012-1077-3
Numerical and experimental evaluation on
methods for parameter identification of thermal response tests
WANG Feng-hao(王沣浩)1, FENG Chen-chen(冯琛琛)1, YAN Liang(颜亮)2,WANG Xin-ke(王新轲)1
1. Building Energy Research Center, Xi’an Jiaotong University, Xi’an 710049, China;
2. Shanghai Architectural Design & Research Institute Co., Ltd., Shanghai 200063, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2012
Abstract: Several parameter identification methods of thermal response test were evaluated through numerical and experimental study. A three-dimensional finite-volume numerical model was established under the assumption that the soil thermal conductivity had been known in the simulation of thermal response test. The thermal response curve was firstly obtained through numerical calculation. Then, the accuracy of the numerical model was verified with measured data obtained through a thermal response test. Based on the numerical and experimental thermal response curves, the thermal conductivity of the soil was calculated by different parameter identification methods. The calculated results were compared with the assumed value and then the accuracy of these methods was evaluated. Furthermore, the effects of test time, variable data quality, borehole radius, initial ground temperature, and heat injection rate were analyzed. The results show that the method based on cylinder-source model has a low precision and the identified thermal conductivity decreases with an increase in borehole radius. For parameter estimation, the measuring accuracy of the initial temperature of the deep ground soil has greater effect on identified thermal conductivity.
Key words: ground source heat pump; thermal response; parameter identification method; numerical simulation
1 Introduction
Borehole heat exchanger (BHE) is a key component of ground source heat pump (GSHP) system, which supplies energy for heating and cooling to buildings. The most popular type of BHE consists of a closed circuit with single or double U-tubes in grouted boreholes, typically 50-200 m deep. For a given building, the dimensions of the BHE installation are determined largely by the thermal conductivity of the deep ground soil. Therefore, it is very important to measure the thermal conductivity of the deep ground soil accurately for the design of ground loops of GSHP systems.
There are several methods to determine the soil thermal conductivity, such as type identification, steady-state test, probe test and thermal response test [1]. By now, thermal response test is widely recognized as the most effective method to determine soil thermal conductivity [1-2]. This approach was firstly proposed by MORGENSEN [3] and then the mobile measurement devices were introduced [1, 4]. During the test, water is constantly heated by the electrical heater or heat pump. A circulating pump is needed to drive the water to circulate in the BHE and release heat to the ambient grout and soil. The inlet and outlet water temperatures as well as the flow rate were measured. Based on the measured results, the soil thermal conductivity can be calculated through parameter identification methods.
Several parameter identification methods have been proposed to calculate the thermal conductivity based on either analytical or numerical solutions of the heat conduction equation, such as least square based on line-source model [1], parameter estimation based on line-source model [2] and parameter estimation based on cylinder-source model [5]. Meanwhile, the accuracy of parameter identification methods is also affected by a number of factors, such as test time, variable data quality, borehole radius, initial ground temperature, and heat injection rate. So, there are significant differences among the thermal conductivities calculated from different parameter identification methods even for the same project [6]. If the relative error of the identified thermal conductivity is 10%, the deviation of the BHE length designed is up to 4.5%-5.8% [4]. The deviation may affect not only initial investment but also safe and effective operation. Therefore, it is very necessary to evaluate the accuracy of different parameter identification methods for the healthy development of GSHP.
Generally speaking, to evaluate parameter identification methods, a BHE installed in an environment that the surrounding soil thermal conductivity had been known should be established. Through thermal response test and parameter identification, the soil thermal conductivity can be identified. By comparing the identified thermal conductivity with the known value, the error of the parameter identification method will be obtained. Both numerical simulation and experimental study are adopted to evaluate parameter identification method in this work.
2 Thermal response curves obtained by 3D finite-volume numerical model based on reference properties of soil
A 3D finite-volume numerical model was established for simulating the procedure of thermal response test. The surrounding soil thermal conductivity of BHE was set up as reference value and used to compare the identified results from the parameter identification methods. The thermal response curves were obtained through numerical calculation.
2.1 Numerical model
The model is proposed based upon the following assumptions: 1) The soil around the borehole is a kind of homogenous medium and the thermal conductivity keeps constant; 2) Moisture migration is ignored; 3) The contact thermal resistances between the U-tube and the backfilling, the backfilling and the soil are neglected; 4) The undisturbed soil is considered as a uniform temperature entity.
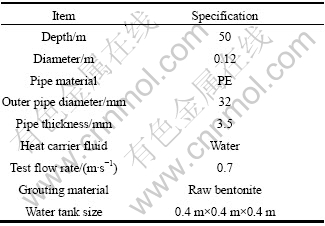
A half computed region is established for the characteristics of symmetry, as shown in Fig. 1(a). The main components of this model contain some fluid in U-tube, a U-tube, backfilling material, soil, two heaters and a tank (Fig. 1(b)). The characteristics of the BHE and the tank are given in Table 1.
Realizable k-ε equation turbulence model is adopted to investigate the performance of BHE, and the general governing equations are written in the unified form as [7]
 (1)
(1)
where ρ is the density of circulating water; f is the generalized physical quantity; u is the velocity of circulating water; Gf is generalized diffusion coefficient; Sf is the generalized source term; t is the time. To avoid boundary effects, the bottom boundary is placed at some distance from the BHE, which is defined as adiabatic boundary. The calculation domain size is 8 m×8 m×53 m. The initial temperature of deep ground soil is 288.6 K.
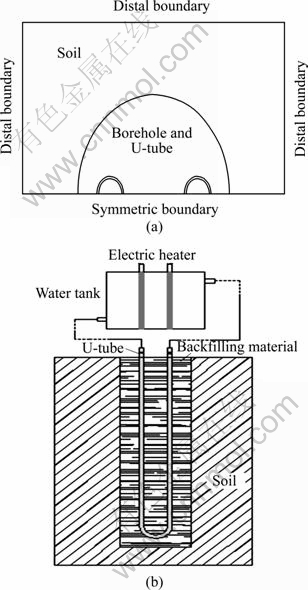
Fig. 1 Half computed region of 3D model (a) and main components of 3D model (b)
Table 1 Characteristics of borehole and water tank in 3D model
The surface temperature of the ground is treated as the third boundary condition. The air temperature is 298.15 K and conductive coefficient is 8 W/m2. The heaters are regarded as the first boundary condition. The heat flux is 15 916 W/m2.
2.2 Thermal response curves
Several studies show that predicting the temperature field changes of a BHE requires a fine computational mesh [8]. In order to determine the optimal sensitivity of the numerical model, four model runs were performed as follows:
1) Run M1: coarse spatial discretization (55 000 meshes)/fine temporal discretization (?t=60 s);
2) Run M2: fine spatial discretization (240 000 meshes)/fine temporal discretization (?t=60 s);
3) Run M3: fine spatial discretization (240 000 meshes)/coarse temporal discretization (?t= 300 s);
4) Run M4: very fine spatial discretization (320 000 meshes)/fine temporal discretization (?t=60 s).
To illustrate the influences of discretization on the model results, the response test is simulated for a period of 200 h (see Fig. 2). After analyzing the thermal response curves, Run M2 is preferred because of the relatively short calculation time involved, and its discretization pattern is used in the following analyses.
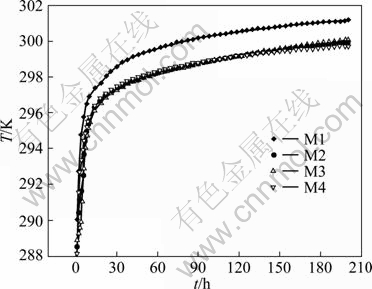
Fig. 2 Simulated mean temperature of recycled water with four different model runs
3 Parameter identification methods
When the thermal response curve is obtained, the thermal conductivity can be calculated by using the parameter identification methods. Several parameter identification methods of thermal response test are introduced.
3.1 Least square based on line-source model
Line-source model is based on Kelvin’s line-source theory and has been applied to simulating the behavior of BHE [9], according to which, at sufficiently long time, the ground heat exchanger can be modeled as an infinite constant-strength line-source within a homogeneous, isotropic and infinite medium, which can be seen as one-dimensional unsteady heat conduction. The temperature field can be expressed as
 (2)
(2)
where T(r,t) is the temperature of the calculated point in the ground where the radius is r and the calculate time is t; T0 is the initial temperature of the ground; q is the heat injection rate per unit borehole depth; λ is the thermal conductivity of soil; α is the thermal diffusivity of the ground. The simplified Ei is defined as
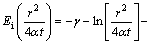
 (3)
(3)
When t≥5r2/α, the borehole wall temperature can be simplified as
 (4)
(4)
where Tw is the borehole wall temperature; γ is Euler constant, 0.577 2.
The borehole resistance is denoted by R0, and the average fluid temperature of the circulation fluid is denoted by Tf. The relation between Tf and Tw can be expressed as Tf –Tw=q·R0. Thus, the average temperature of the circulation fluid can be written as
 (5)
(5)
where rb is the diameter of the borehole.
If q is constant, Eq. (5) becomes a simple liner relation as
 (6)
(6)
where k is defined as k=q/4πλ, m is a constant, and Tf is confirmed by the following equation:
 (7)
(7)
Given the rate of heat injection to the loop (q) and the inlet (Tin) and the outlet (Tout) temperatures of the circulation fluid as a function of time, the thermal conductivity (λ) can be determined.
3.2 Parameter estimation based on line-source model
Base on Eq. (4), when t≥5r2/α, the borehole wall temperature can be simplified as
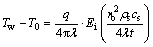 (8)
(8)
where ρs is the soil density; cs is the speci?c heat of soil. The average temperature of the circulation fluid can also be described as
 (9)
(9)
Initial ground temperature (T0) must be measured and is considered as a known parameter with this method. Thus, three unknown parameters, R0, λ and ρscs need to be identified by some optimization techniques, such as parameter estimation. The standard procedure is to minimize the difference between the average temperature of the fluid calculated from parameter identification method and the 3D numerical model according to the adjustment of the data of R0, λ and ρscs contained in Eq. (9). The objective function for this optimization procedure is given by
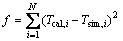 (10)
(10)
where Tsim,i is the mean water temperature at the time point i which is measured or calculated by the numerical model; Tcal,i is the mean water temperature at the time point i which is calculated by the heat transfer model. When f is the minimum, the results of the thermal conductivity (λ), the volume specific heat capacity (ρscs ) as well as the borehole resistance (R0) are found. The calculation process is shown in Fig. 3.
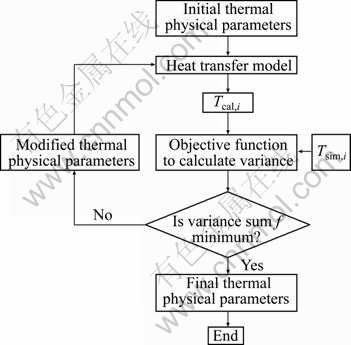
Fig. 3 Calculation process of parameter estimation method
3.3 Parameter estimation based on cylinder-source model
Ground heat exchanger is modeled as a cylindrical with a certain radius and a constant heat flux to a homogeneous, isotropic and infinite medium with the cylinder source method. The temperature field is given by [9]
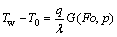 (11)
(11)
where Fo is Fourier’s number and is defined as Fo=αt/rb2;G (Fo, p) is theoretical integral solution of the function G, and p=r/r0. Some characteristic solutions were presented by CARSLAW and JAEGER [10]. For example, when p=1 and Fo lies between 0.1 and 106, the characteristic solution of the function G can be simplified as
 (12)
(12)
When p=1, the average fluid temperature of the circulation fluid can also be described as
 (13)
(13)
where Tff is the far ?eld soil temperature. Equation (13) also contains three unknown parameters: R0, λ and ρscs, which can be obtained by parameter estimation method described above.
3.4 Parameter identification results
Thermal conductivity was calculated from M2 curve by the methods mentioned above. The calculated results are given in Table 2.
As shown in Table 2, there is little difference between the accuracy of the result obtained from the methods based on line-source model. But for the method based on cylinder-source model, the result is smaller than the assumed value, and has a low precision.
4 Thermal response test
In order to verify the accuracy of the numerical model and calculate the soil thermal conductivity through measured thermal response curve with different parameter identification methods of thermal response test, an experiment table of ground source heat pump and a test vehicle were constructed in Xi’an Jiaotong University, China. The experiment table is illustrated in Fig. 4.
Table 2 Calculated results of different parameter identification methods
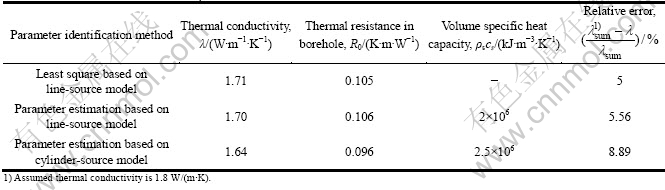
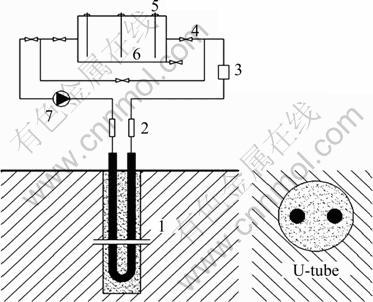
Fig. 4 System diagram of ground source heat pump experiment table and test vehicle: 1-PE pipe; 2-Thermal resistance PT100; 3-Flowmeter; 4-Valve; 5-Electric heater; 6-Water tank; 7-Water pump
For the experiment table, a vertical 50 m-deep well was completed with a PE U-tube. The well was grouted with coarse sand and protoplasm. The external diameter and the wall thickness of the U-tube were 32 mm and 3.5 mm, respectively.
4.1 Initial average temperature of ground
To test the initial average temperature, the U-tube was filled with water for several days. After the standing time, open the pump and test the inlet and outlet water temperatures of the U-tube under the condition that there was no heat injection in the water tank. The initial average temperature of the ground could be obtained when the inlet and outlet temperatures were the same (2% difference between the two temperatures was allowed). Figure 5 shows the curve of the inlet and outlet temperatures with time. As shown in Fig. 5, the temperature tends to be stable at around 289.35 K after 140 min. This indicates that the temperatures of the water in the U-tube and the ground are nearly the same, and the heat conduction can be neglected. Therefore, the stable temperature is the initial average temperature of the ground.
4.2 Thermal response test
The electric heater should be opened to conduct the thermal response test. The heating power of the electric heater was 2.1 kW. The rate of water flow in the U-tube was set to be 1.10 m?/h by controlling the pump and the opening of the valve. The thermal response test curve is shown in Fig. 6.
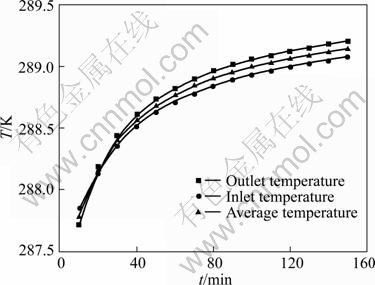
Fig. 5 Measured inlet and outlet temperatures of U-tube with time during initial average temperature test of ground
As we can see from Fig. 6, the measured thermal response test curve has a lager fluctuation compared with the curve got from the numerical simulation. This may be affected by the weather and the power-supply fluctuations. The temperature of the water in the U-tube is around 302.0 K after 40 h, which is basically stable.
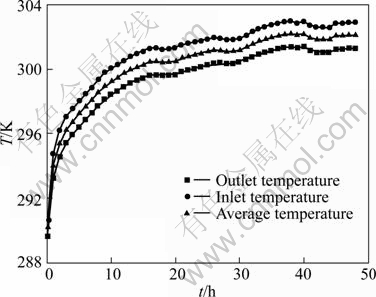
Fig. 6 Measured inlet and outlet temperatures of U-tube with time during thermal response test
4.3 Verification of 3D numerical model
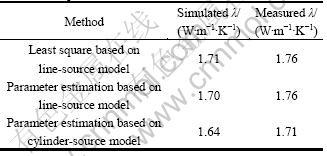
The measured results can be got from the measured thermal response test curve with the parameter identification methods mentioned above. The measured and calculated results are summed up in Table 3. As we can see, the simulated results agree the measured results well, which verifies the accuracy of the numerical model established.
The results of the parameter estimation based on cylinder-source model are smaller than those of line-source model. This is because of the simplification of the model.
The results indicate that the calculated average temperature has a good agreement with the measured average temperature. This indicates that the parameter identification methods used in this work are valid.
Table 3 Comparison of measured and calculated results
5 Analysis of influence factors
5.1 Influence of test time on ground thermal conductivity
The calculated thermal conductivity with test time is shown in Fig. 7.
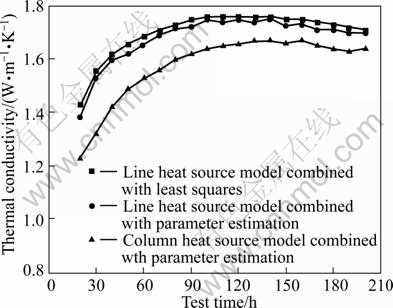
Fig. 7 Ground thermal conductivity changes with test time with different parameter identification methods
It is inferred that the soil thermal conductivity is lower than the assumed reference value when the test time lasts for 70 h or more for all parameter identification methods. Furthermore, the two-parameter identification methods based on line-source model agree with each other significantly, while the identified thermal conductivity is smaller based on cylinder-source method compared with the line-source model. In conclusion, for all test methods, the results are stable when the measured time lasts for 70 h or more.
5.2 Variable data quality
Some simplifications and assumptions are carried out in Eqs. (2)-(5). The data obtained at the beginning of the test should be abandoned for they don’t satisfy the assumptions. But, there is no uniform standard to explain how much data should be abandoned. The influence of different starting time (t0) on the identified thermal conductivity is shown in Fig. 8. It is inferred that the identified results increase as the starting time increases before 40 h and keep invariant when t0 is up to 40 h or more. The difference of the identified thermal conductivity reaches 3% between the starting time of 5 h and 40 h.
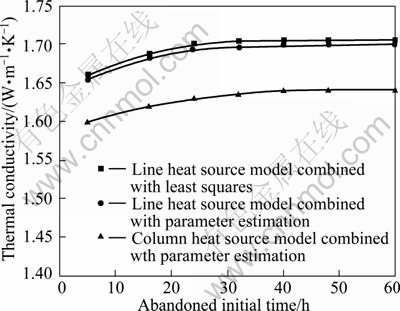
Fig. 8 Ground thermal conductivity changes with abandoned initial time with different parameter identification methods
5.3 Borehole radius
The heat flux is assumed to impose at r=0 in line-source model, while r=rb is assumed in cylinder- source model. Therefore, the borehole radius may be an influence factor to identify the thermal conductivity. The results are illustrated in Fig. 9. It can be confirmed that the borehole radius almost has no effect on the identified thermal conductivity of the two-parameter identification methods based on line-source model. The identified thermal conductivity decreases as the borehole radius increases with the method based on cylinder-source, and the difference between the thermal conductivities obtained from r=0.05 and r=0.12 is up to 16.08%. Moreover, compared with the line-source model, the relative error of accuracy is larger at the same borehole radius, which may be caused by the simplifications and assumptions of the theoretical model.
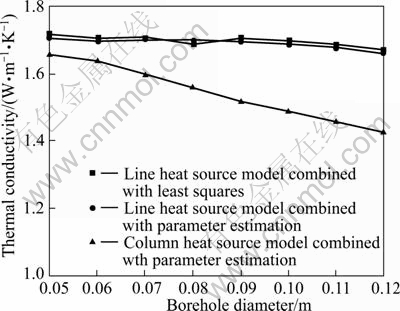
Fig. 9 Ground thermal conductivity changes with borehole diameter with different parameter identification methods
5.4 Initial ground temperature
With vast territory, different geological and climatic conditions, the initial ground temperature in China has a great difference from east to west and from north to south, which can reach up to 6 K or more. Therefore, it is significant to research the adaptability of parameter identification methods in different regions. The results obtained from different initial ground temperatures are illustrated in Fig. 10. Figure 10 shows that the identified thermal conductivities are almost invariant practically. This seems to suggest that all parameter identification methods in this work have good universality.
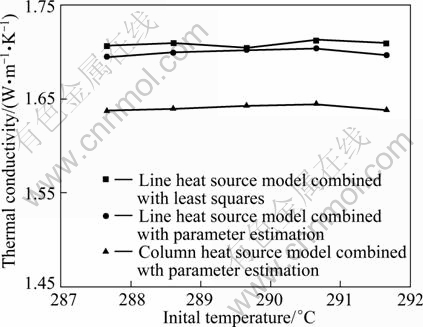
Fig. 10 Ground thermal conductivity changes with initial ground temperature with different parameter identification methods
From Section 3.2, it is known that the initial ground temperature (T0) is conceived as a known parameter in parameter estimation method. That is to say, the initial ground temperature should be measured in parameter estimation. When actual temperature measurement errors are considered, the identified results will be different, as shown in Fig. 11. For least square based on line-source model, the identified results maintain at an invariable level because the initial ground temperature is not an essential parameter in parameter identification. When the temperature measurement error is 1 K, the deviation of identified result based on line-source model is up to 10%-12%, while it is up to 6%-18% for the method based on column-source model.
5.5 Heat injection rate
Thermal response test is generally performed by injecting hot fluids into the U-tube but no theoretical investigations that account for heat injection rate effects have been done so far. The influence of heat injection rate on the identified thermal conductivity is discussed, as shown in Fig. 12.
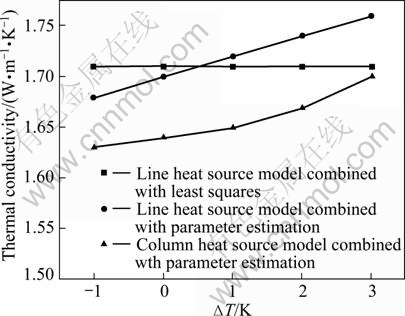
Fig. 11 Ground thermal conductivity changes with actual temperature measurement errors with different parameter identification methods
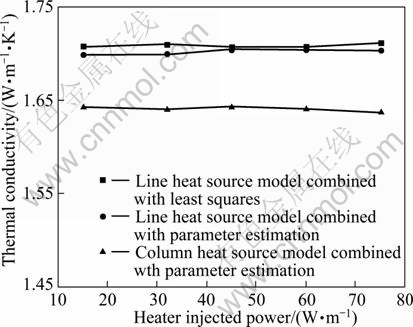
Fig. 12 Ground thermal conductivity changes with heater injected power with different parameter identification methods
As shown in Fig.12, the identified results obtained from different methods are stabilized at 1.71, 1.70 and 1.64 W/(m·K), respectively. However, ZHOU and LEI’s researches showed that the identified thermal conductivity increased as the heat injection rate increased, which may be caused by groundwater flow [11]. The effects of groundwater flow on the identified results of thermal response test have been discussed by several authors and those studies have shown that these effects are significant. It was indicated that the identified thermal conductivity can not be directly applied in the design of heat exchanger where there is significant groundwater flow (i.e. when the Peclet number, Pe, is greater than 1) [12-13]. In conclusion, if groundwater flow is very slow and heat conduction is stronger than heat convection, the influence of the heat injection rate could be neglected, but this simplification is invalid when there is significant water movement. The inlet (Tin) temperature of the circulation fluid should be consistent with the nominal working condition of heat pump unit.
6 Conclusions
1) To ensure the stability, the test time should last for beyond 70 h.
2) The parameter identification method based on the line-source model has a higher precision compared with cylinder-source model.
3) Early starting time is strongly influenced by the thermal response of the BHE itself. A suggestion that the initial test data should be abandoned moderately to improve the accuracy is presented.
4) The observed influence of the borehole radius on the results suggests that the cylinder-source model can not be used to predict the performance of BHE when the borehole radius is large.
5) All parameter identification methods mentioned above have good universalities, which can be used in different regions.
6) When the heat exchange is considered as pure heat conduction, there is little influence of the heater injection power on the identification of the ground thermal conductivity. For practical test, the identified thermal conductivity increases as the heat injection rate increases if groundwater flow is significant. Further investigations on this topic will help us to gain a better understanding of this effect.
References
[1] AUSTIN W A. Development of an in situ system for measuring ground thermal properties [D]. Oklahoma: Oklahoma State University, 1998.
[2] YU M Z, PENG X F. A simplified model for measuring thermal properties of deep ground soil [J]. Experimental Heat Transfer, 2004, 17(2): 119-130.
[3] MOGENSEN P. Fluid to duct wall heat transfer in duct system heat storages [C]// Proceedings of International Conference on Subsurface Heat Storage in Theory and Practice. Stockholm, Sweden, 1983: 652-657.
[4] EKLl?F C, GEHLIN S. TED-A mobile equipment for therma1 response test [D]. Sweden: Lulea University of Technology, 1996.
[5] ZHAO Jun, DUAN Zheng-qiang. A method for in-situ determining underground thermal properties based on the cylindrical heat source model [J]. Acta Energiae Solaris Sinica, 2006, 27(9): 934-936.
[6] XU W. Analysis of the development strategy and engineering application of ground source heat pump [J]. Construction & Design for Project, 2008(1): 12-13.
[7] TAO Wen-quan. Numerical heat transfer [M]. Xi’an: Xi’an Jiaotong University Press, 2001: 28-129.
[8] KOHL T, HOPKIRK R J. “FRAC Ture”-A simulation code for forced ?uid ?ow and transport in fractured porous rock [J]. Geothermics, 1995, 24: 345-359.
[9] INGERSOLL L R, PLASS H J. Theory of the ground pipe heat source for the heat pump [J]. ASHRAE Transactions, 1948, 54(7): 339-348.
[10] CARSLAW H S, JAEGER J C. Conduction of heat in solids, 2nd ed [M]. Oxford, UK: Oxford University Press, 1959: 57-84.
[11] ZHOU Ya-su, LEI Ming. Influence factors analysis on in situ test of ground thermal conductivity [J]. Journal of Donghua University, 2009, 35(4): 472-477. (in Chinese)
[12] KATSURA T, NAGANO K, TAKEDA S. Heat transfer experiment in the ground with ground water advection [C]// Proceedings of 10th Energy Conservation Thermal Energy Storage Conference. Ecostock’ 2006. New Jersey, 2006: 1-27.
[13] RAYMOND J, THERRIEN R, GOSSELIN L, LEFEBVRE R. Numerical analysis of thermal response tests with a groundwater flow and heat transfer model [J]. Renewable Energy, 2011, 36: 315-324.
[14] LAMARCHE L, BEAUCHAMP B. A new contribution to the finite line-source model for geothermal boreholes [J]. Energy and Buildings, 2007, 39(2): 188-198.
[15] BOZDAG S, TURGUT B, PAKSO Y H, DIKICI D, MAZMAN M, EVLITYA H. Ground water level in?uence on thermal response test in Adana, Turkey [J]. International Journal of Energy Research, 2008, 32(7): 629-633.
[16] SIGNORELLI S, BASSRTTI S, PAHUD D, KOHL T. Numerical evaluation of thermal response tests [J]. Geothermics, 2007, 36: 141–166.
[17] ASHRAE. 2007 ASHRAE handbook on HVAC applications [M]. Atlanta: American Society of Heating, Refrigerating and Air-conditioning Engineers, Inc, 2007.
[18] IGSHPA (international ground source heat pump association). Closed-Loop/Geothermal heat pump systems-design and installation standards (2007 Edition) [M]. USA: Oklahoma State University, 2007: 1-28.
[19] SHARQAWY M H, MOKHEIMER E M, HABIB M A, BADR H M, SAID S A, Al-SHAYEA N A. Energy, exergy and uncertainty analyses of the thermal response test for a ground heat exchanger [J]. International Journal of Energy Research, 2009, 33(6): 582-592.
[20] MARCOTTE D, PASQUIER P. On the estimation of thermal resistance in borehole thermal conductivity test [J]. Renewable Energy 2008, 33: 2407-2415.
[21] BOZDA-G S, TURGUT B, PAKSOY H, DIKICI D, MAZMAN M, EVLIYA H. Ground water level influence on thermal response test in Adana, Turkey [J]. International Journal of Energy Research, 2008, 32(7): 629-633.
[22] FUJII H, OKUBO H, NISHI K., ITOI R, OHYAMA K, SHIBATA K. An improved thermal response test for U-tube ground heat exchanger based on optical fiber thermometers [J]. Geothermics, 2009, 38, 399-406.
[23] FLORIDES G, KALOGIROU S. First in situ determination of the thermal performance of a U pipe borehole heat exchanger, in Cyprus [J]. Applied Thermal Engineering, 2008, 28(2/3): 157-163.
(Edited by YANG Bing)
Foundation item: Project(xjj20100078) supported by the Fundamental Research Funds for the Central Universities in China
Received date: 2011-07-26; Accepted date: 2011-11-14
Corresponding author: WANG Feng-hao, Professor, PhD; Tel: +86-13227006940; E-mail: fhwang@mail.xjtu.edu.cn