Energy efficient resource allocation for D2D multicast communications
来源期刊:中南大学学报(英文版)2019年第11期
论文作者:左加阔 杨龙祥
文章页码:3034 - 3044
Key words:D2D; energy efficiency; resource allocation; max-min fairness criterion; fractional programming
Abstract: The resource allocation for device-to-device (D2D) multicast communications is investigated. To achieve fair energy efficiency (EE) among different multicast groups, the max-min fairness criterion is used as the optimization criterion and the EE of D2D multicast groups are taken as the optimization objective function. The aim is to maximize the minimum EE for different D2D multicast groups under the constraints of the maximum transmit power and minimum transmit rate, which is modeled as a non-convex and mixed-integer fractional programming problem. Here, suboptimal resource allocation algorithms are proposed to solve this problem. First, channel assignment scheme is performed to assign channel to D2D multicast groups. Second, for a given channel assignment, iterative power allocation schemes with and without loss of cellular users’ rate are completed, respectively. Simulation results corroborate the convergence performance of the proposed algorithms. In addition, compared with the traditional throughput maximization algorithm, the proposed algorithms can improve the energy efficiency of the system and the fairness achieved among different multicast groups.
Cite this article as: ZUO Jia-kuo, YANG Long-xiang. Energy efficient resource allocation for D2D multicast communications [J]. Journal of Central South University, 2019, 26(11): 3034-3044. DOI: https://doi.org/10.1007/ s11771-019-4234-0.

J. Cent. South Univ. (2019) 26: 3034-3044
DOI: https://doi.org/10.1007/s11771-019-4234-0
ZUO Jia-kuo(左加阔)1, YANG Long-xiang(杨龙祥)2
1. College of Internet of Things, Nanjing University of Posts and Telecommunications,Nanjing 210003, China;
2.College of Telecommunications & Information Engineering, Nanjing University of Posts andTelecommunications, Nanjing 210003, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Abstract: The resource allocation for device-to-device (D2D) multicast communications is investigated. To achieve fair energy efficiency (EE) among different multicast groups, the max-min fairness criterion is used as the optimization criterion and the EE of D2D multicast groups are taken as the optimization objective function. The aim is to maximize the minimum EE for different D2D multicast groups under the constraints of the maximum transmit power and minimum transmit rate, which is modeled as a non-convex and mixed-integer fractional programming problem. Here, suboptimal resource allocation algorithms are proposed to solve this problem. First, channel assignment scheme is performed to assign channel to D2D multicast groups. Second, for a given channel assignment, iterative power allocation schemes with and without loss of cellular users’ rate are completed, respectively. Simulation results corroborate the convergence performance of the proposed algorithms. In addition, compared with the traditional throughput maximization algorithm, the proposed algorithms can improve the energy efficiency of the system and the fairness achieved among different multicast groups.
Key words: D2D; energy efficiency; resource allocation; max-min fairness criterion; fractional programming
Cite this article as: ZUO Jia-kuo, YANG Long-xiang. Energy efficient resource allocation for D2D multicast communications [J]. Journal of Central South University, 2019, 26(11): 3034-3044. DOI: https://doi.org/10.1007/ s11771-019-4234-0.
1 Introduction
Improving the spectrum efficiency and energy efficiency is the critical issue in the future wireless networks [1]. Device-to-device (D2D) communication, as a new communication technology, has gained much attention because of its potential for resource utilization. By allowing two proximity users to transmit signal directly, D2D communications can bring numerous benefits including the proximity gain, the reuse gain and the hop gain [2, 3]. Since the users’ terminals are handheld equipment with limited battery life, energy efficient design has become more and more imperative in D2D communications [4].
To maintain the quality of service (Qos) for macro cell users and secondary cell users, ALQERM et al [5] proposed a distributed intuition-based online learning power allocation algorithm. WU et al [6] considered the spectrum- power cooperation between D2D users (DUs) and cellular users (CUs) for uplink transmission in D2D communications. A low complexity suboptimal algorithm and an optimal algorithm were proposed for the case of public-interest DUs and self-interest DUs respectively. The resource allocation problem was addressed by ZHOU et al [7] based on one-to-one matching approach, and an iterative power allocation algorithm was developed based on non-linear fractional programing. By exploiting the properties of fractional programming, JIANG et al [8] transformed the original non-convex energy efficient resource allocation problem into an equivalent optimization problem, and then an iterative resource allocation scheme was proposed. LEE et al [9] considered both energy efficient (EE) power control problem and the eavesdropper in heterogeneous networks, and proposed a power control scheme for improving EE. FENG et al [10] proposed a centralized energy-efficient optimization framework for D2D communications by joint mode selection and power allocation. Dinkelbach method and concave-convex procedure were adopted to transform the optimization problems into sequential convex approximations. ZHOU et al [11] modeled resource allocation problem as a non-cooperative game, and investigated the tradeoff between EE and spectrum efficiency. Under cloud radio access network, ZHOU et al [12] studied the resource allocation problem for D2D communications and proposed a hybrid algorithm, which consists of a centralized interference mitigation algorithm and a distributed joint channel selection and power allocation algorithm. GUO et al [13] considered joint optimization problem of mode selection, subcarrier assignment and power allocation and two suboptimal methods are derived based on Lagrangian decomposition method and low- complexity decomposition method. ZHOU et al [14] studied the maximization problem of EE in an interference-limited environment and a distributed interference-aware resource allocation algorithm was proposed. Wireless energy and information transfer for D2D network was studied by DENG et al [15], and three wireless energy transfer policies were proposed. In addition, in the information transfer phase, a new notion of transmission efficiency from a network view was introduced. A new energy saving paradigm was proposed by CHANG et al [16], which named as collaborative mobile cloud (CMC). CMC can be used to solve the signaling overhead problem in D2D communications.
However, the above research works only consider the EE of the D2D networks under non- multicast communication, which improve the networks EE at the cost of users in the bad channel conditions, and ignore the EE of the individual users. Thus, network EE optimization gives rise to unfairness among users. In this paper, we aim to solve the above problems. The major contributions of this paper are as follows:
1) We study the energy efficient resource allocation problem for D2D multicast communications. By considering the fairness among different multicast groups, the max-min fairness criterion is used as the resource allocation criterion. The energy efficient resource allocation problem is formed into a non-linear fractional max-min problem.
2) To solve the above problem, we divide the original problem into two sub-problems: channel assignment problem and power allocation problem. We propose two algorithms to the two sub- problems, respectively. For channel assignment problem, a new heuristic channel assignment algorithm is proposed. For a given channel assignment, power allocation problems with and without loss of cellular users’ rate are considered. Then, two iterative power allocation schemes are proposed based on fractional programming and sequential convex programming.
3) The simulation numerically evaluates the performance of the proposed resource allocation algorithms. In particular, the proposed algorithms can improve the energy efficiency compared with traditional throughput maximization algorithm. Simulation results also demonstrate that our proposed algorithms can guarantee energy efficiency fairness among multicast groups.
2 System model and problem formulation
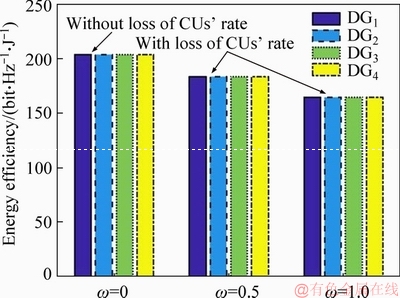
Consider the uplink scenario of a single cellular network, which is composed of the base station (BS), D2D multicast groups (DMGs) and cellular users, as shown in Figure 1. The numbers of CUs and DMGs are C and J (J Figure 1 System model of D2D multicast communication Assume that the c-th channel is reused by the j-th DMG, and then the rate of the c-th CU is defined as: where Wc is the bandwidth for CUc; pc is the transmit power of the c-th CU; Let where Since the capacity of DMG is restricted by the DR with the worst channel condition, let Therefore, the aggregate rate for the j-th DMG on the c-th channel is: Note in the above discussion, the loss of CUs’ rates caused by the DMGs is not considered. By introducing the loss of CUs’ rate, we define: where the second term in the right hand size denotes the loss of the c-th CU’s rate; ωj (0≤ωj≤1) is the weight factor for the loss of the CUs’ rate in the j-th DMG. Observe that when ωj=0, Let where κj is the inverse of the power amplifier efficiency and To maximize the EE of the worst DMG link, the jointly channel and power allocation optimization problem can be formulated as: where Rreq is the required transmit rate; Pth is the power budget; C1 is the minimum transmit rate requirement constraint; C2 and C3 are the transmission power constraints; C4 and C5 indicate that each channel resource of CUs cannot be shared by multiple DMGs. For convenience, the key notes used in this paper are listed in Table 1. Table 1 Summary of key notation 3 Proposed resource allocation scheme Obviously, Eq. (7) is a mixed integer non- linear fractional programming problem. It is in general difficult to solve. In this section, a two- stage approach, which contains two individual procedures, is proposed to solve the above problem. 3.1 Channel assignment algorithm In this section, heuristic channel assignment algorithm is proposed to maximize the minimum individual EE, under the constraints C1-C5. According to the constraints C1-C3, there is Let Ωj denote the channel set for the j-th DMG, and the proposed heuristic channel assignment algorithm is tabulated as Algorithm 1. In the first step, each DMG is allocated to a channel with the highest value 3.2 Power allocation algorithm For a given channel assignment, the optimization problem Eq. (7) is transformed into the following form: s.t. C1-C3 (8) However, the above optimization problem is still non-convex. Fractional programming [19, 20] Algorithm 1 Channel assignment 1: Set 2: For each 3: Find 4: Calculate 5: Update 6: End for 7: While 8: Find 9: Find 10: If 11: Update 12: Calculate 13: End if 14: End while is usually used to solve the above problem. Let where Let p* and λ* be the optimal solution and optimal objective of Eq. (8), respectively: Theorem 1: Eqs. (8) and (9) have the same set of optimal solutions, if and only if: Proof: See Appendix A. Similar proof can be found in Refs. [21, 22]. By Theorem 1, it is clear that solving problem in Eq. (8) can be achieved by finding a solution of the equation F(λ*)=0. However, λ* is unknown. To determine the optimal λ*, the generic Dinkelbach algorithm [23] is adopted. Combining with constraints C1-C3, Plb and Pub, which denote the minimum and the maximum power consumption respectively, are given as follows: where Introduce two new variables αmin and αmax, where αmin≥αmax. Define an interval [αmin, αmax] which contains λ*. Then at the t-th iteration, αmin and αmax can be updated via: The proposed iterative power allocation algorithm is described as Algorithm 2. Algorithm 2 Iterative power allocation algorithm 1: Calculate Plb and Pub 2: Set t=1 and 3: Choose 4: Repeat 5: For the given λt, 6: Solve problem in Eq. (9) to obtain pt 7: Calculate 8: Update the interval 9: Update 10: If 11: Let t=t+1 12: End if 13: End for 14 Until Similar convergence proof of Algorithm 2 can be found in Ref. [23]. In step 2, problem in Eq. (9) is needed to be solved. In the following, how to solve this problem is discussed. 3.2.1 Without loss of CUs’ rate (wj=0) Since wj=0, Problem in Eq. (16) is convex optimization problem which can be solved efficiently by interior-point algorithm [24]. The computational complexity to solve Eq.(16) is o((JC)3). Since the proposed algorithm without loss of CUs’ rate includes two loops: outer loop (i.e., Algorithm 2) and interior-point (i.e., interior-point algorithm to solve Eq.(16)), the total computational complexity of the algorithm without loss of CUs’ rate is o(tmax(JC)3), where tmax is the maximum iteration number of outer loops (i.e., Algorithm 2). 3.2.2 With loss of CUs’ rate (0 In this case, where φj(p) and fj(p) are concave for p. Then, Eq. (9) can be expressed by: Since φj(p) and fj(p) are concave for p, φj(p)- fj(p) is a D.C (difference of two concave functions) function [25], which can be effectively solved by sequential convex programming [26]. Let pτ be the power allocation at step τ, and pτ+1 is updated by solving the following convex problem: As in Eq. (16), further transform Eq. (20) into a smooth and standard convex optimization problem: where where n is the index of the Eq. (21) is convex optimization problem, which can be solved efficiently by interior-point algorithm [24]. The detailed process for solving Eq. (9) with the loss of CUs’rate is given as Algorithm 3. Similar convergence analysis of Algorithm 3 can be find in Refs. [26, 27]. Now, we have presented the power allocation algorithm to solve Eq. (8), when the loss of CUs’rate is considered. The algorithm with loss of CUs’ rate includes two loops: outer loop (i.e., Algorithm 2) and inner loop (i.e., Algorithm 3 and interior-point algorithm to solve Eq. (21)). Algorithm 3 Algorithm for solving problem Eq. (9) 1: Choose p0 and calculate 2: Repeat 3: Solve problem Eq. (21) to obtain the solution 4: Set τ=τ+1 and 5: Calculate 6: Until Let χ denote the total cost of computing fj(p), and its first and second derivatives. The computational complexity of Algorithm 3 is 4 Performance analysis In this section, some numerical results are presented to evaluate the performance of the proposed schemes. Considering that there are 12 cellular users and 4 D2D multicast groups located randomly in a single cell. The BS is located at the center of the cell. The channel gains are assumed to be Rayleigh-fading with an average power gain of 0 dB. Without loss of generality, set Mj=5,Wc=1 MHz, pc=15 dBm, κj=1, For convenience, we use WoL algorithm and WL algorithm to denote resource allocation algorithms without and with loss of CUs’ rate, respectively. Figure 2 illustrates the evolution of WoL algorithm and WL algorithm. In Figure 2, set Pth=12 dBm and Rreq=1 Mbps. Note that the algorithm with loss of CUs’ rate consists of two loops, and the effect of outer loop iterations t is only considered. It is observed that both of the algorithms converge to the optimal λ fast. We also find that WL algorithm converges faster than WoL algorithm. According to Algoirthm 2, the optimal λ* must be in the interval The size of interval Figure 2 Convergence evolution of proposed algorithms Figure 3 depicts the EE of the worst case DMG versus weight factor ω for different power budget with Rreq=1 Mbps. Weight factor ω reflects the loss of CUs’ rates caused by the DMGs. In Figure 3, when ω=0, the algorithm becomes WoL algorithm; When Figure 3 EE of the worst case DMG vs weight factor To emphasize the advantages of the proposed schemes, the proposed algorithms with the algorithm in Ref. [28] are compared. For the sake of fairness, the channel allocation and power allocation of D2D users in Ref. [28] are only considered, and set Rreq=1 Mbps. Let the number of D2D multicast groups J=1. Figure 4 depicts the EE of the two algorithms versus the power budget. As can be seen in Figure 4, the EE performance of the proposed algorithms has similar performance, and both of the algorithms can improve the EE compared with the algorithm in Ref. [28]. Because the weight factor ω=0.5 is very small, the algorithm with CUs’rate has similar performance with the algorithm without CUs’rate, and both of the proposed algorithms can always select the optimal power that achieves the highest EE, while the algorithm in Ref. [28] is to maximize the throughput of system. Figure 4 EE comparison of proposed algorithms and algorithm in Ref. [28] The EE as a function of the minimal rate requirement in Figure 5 is investigated, where Pth=12 mW. As shown in Figure 5, the EE decreases with the growth of the rate requirements. This is because when the rate requirement is high, in order to meet the rate requirement, much power is allocated to the D2D users (the growth of rate requirements will result in exponentially increase of power consumption). At the same time the growth of the rate requirements also results in more frequently system outage. In addition, the proposed algorithms have higher EE than the algorithm in Ref. [28]. The reason is the same as the reason analyzed in Figure 4. Figure 6 shows the system throughput of the proposed algorithms and algorithm in Ref. [28] versus power budget. As can be seen, the algorithm in Ref. [28] outperforms the proposed algorithms; at the high power budget region, the throughput of the proposed algorithms become saturated. This is because the algorithm in Ref. [28] is throughput maximization algorithm, which uses all the available power to maximize its throughput, and thus the energy efficiency is impaired. While, the proposed algorithms tend to reduce the transmit power to maximize the system energy efficiency. Figure 5 EE versus minimal rate requirement Figure 6 Throughput comparison of proposed algorithms and algorithm in Ref. [28] The EE of the worst case DMG versus the power budget is depicted in Figure 7 where Rreq=1 Mbps. As can be seen in Figure 7, the EEs of the two algorithms increase with the increasing of the power budget at the beginning. When the power budget is sufficient enough, the EE remains almost unchanged. This is because the lower the power budget is, the more the D2D multicast communications network suffers outage. The fairness of the proposed algorithm in resource allocation is also investigated. Usually,the fairness index is used to measure the fairness of the algorithm [29], and is defined as: Figure 7 EE of the worst case DMG vs power budget Figure 8 Fairness index vs number of DMGs The EEs of each DMG under the resource allocation algorithms with and without loss of CUs’ rate are compared in Figure 9, where Pth=12 dBm and Rreq=1 Mbps. As shown in Figure 9, the EE fairness among DMGs is guaranteed in both of the proposed algorithms. Figure 9 EE of each DMG under proposed algorithms 5 Conclusions In this paper, a max-min energy efficiency- optimal problem for D2D multicast communications is studied by integrating both channel assignment and power allocation. In addition, both with and without loss of cellular users’ rate are considered in formulated optimization problem. To solve above nonsmooth and mixed integer fractional programming problem, two-step resource allocation algorithms are proposed. Numerical results show that our proposed algorithms can guarantee energy efficiency fairness among multicast groups and improve the energy efficiency of D2D multicast groups. For future work, we will consider the impact of imperfect channel state information on the energy efficiency and how to obtain the optimal solution of the formulated energy efficient problem. Appendix A Before proving Theorem 1, the following lemma is given: Lemma 1:If and only if λ<λ*, there is F(λ)>0. Therefore, F(λ*)≤0. Proof:Assuming F(λ)≥0, there is a solution p0 ( Eq. (A-1) is equivalent to Therefore, when F(λ)≥0, there is λ<λ*. Assuming λ<λ*, there is a solution p1 Equation (A-3) is equivalent to the following inequality: Therefore, when λ<λ*, there is F(λ)>0. In summary, if and only if λ<λ*, F(λ)>0. In addition, since In the following, the proof of Theorem 1 combining with the above Lemma 1 is presented. 1) Assume that p* is the optimal solutions of Eq. (8), since According to F(λ*)≤0 in Lemma 1, there is F(λ*)=0. Therefore, the optimal solution of Eq. (8) makes F(λ*)=0. 2) Assuming F(λ*)=0, p* is the optimal solutions of Eq. (9), then: Equation (A-6) can be rewritten as following form: Therefore, p* is also the optimal solution of Eq.(8). Combing with the analysis of (17) and (27), Theorem 1 is proved. References [1] LEI Ke-jun, TAN Yang-hong, YANG Xi, WANG Han-rui. A K-means clustering based blind multiband spectrum sensing algorithm for cognitive radio [J]. Journal of Central South University, 2018, 25(10): 2451-2461. DOI: 10.1007/s11771- 018-3928-z. [2] JAMEEL F, HAMID Z, JABEEN F, ZEADALLY S, JAVED M A. A survey of device-to-device communications: Research issues and challenges [J]. IEEE Communications Surveys & Tutorials, 2018, 20(3): 2133-2168. DOI: 10.1109/COMST. 2018.2828120. [3] ZUO Jia-kuo, YANG Long-xiang. Energy efficient power allocation for D2D communications in fading channels [J]. Electronics Letters, 2018, 54(3): 177-179. DOI: 10.1049/ el.2017.3875. [4] KLAIQI B, CHU Xiao-li, ZHANG Jie. Energy- and spectral-efficient adaptive forwarding strategy for multi-hop device-to-device communications overlaying cellular networks [J]. IEEE Transactions on Wireless Communications, 2018, 17(9): 5684-5699. DOI:10.1109/TWC. 2018.2846222. [5] ALQERM I, SHIHADA B. Energy-efficient power allocation in multitier 5G networks using enhanced online learning [J]. IEEE Transactions on Vehicular Technology, 2017, 66(12): 11086- 11097. DOI:10.1109/TVT.2017.2731798. [6] WU Qing-qing, LI G Y, CHEN Wen, NG D W K. Energy-efficient D2D overlaying communications with spectrum-power trading [J]. IEEE Transactions on Wireless Communications, 2017, 16(7): 4404-4419. DOI: 10.1109/ TWC.2017.2698032. [7] ZHOU Zhen-yu, OTA K, DONG Mian-xiong, XU Chen. Energy-efficient matching for resource allocation in D2D enabled cellular networks [J]. IEEE Transactions on Vehicular Technology, 2017, 66(6): 5256-5268. DOI: 10.1109/TVT.2016. 2615718. [8] JIANG Yan-xiang, LIU Qiang, ZHENG Fu-chun, GAO Xi-qi, YOU Xiao-hu. Energy-efficient joint resource allocation and power control for D2D communications [J]. IEEE Transactions on Vehicular Technology, 2016, 65(8): 6119-6127. DOI: 10.1109/TVT.2015.2472995. [9] LEE K, HONG J P. Power control for energy efficient D2D communication in heterogeneous networks with eavesdropper [J]. IEEE Communications Letters, 2017, 21(11): 2536-2539. DOI: 10.1109/LCOMM.2017.2718521. [10] FENG Da-quan, YU Guan-ding, XIONG Cong, YI Yuan-wu, LI G Y, FENG Gang, LI Shao-qian. Mode switching for energy- efficient device-to-device communications in cellular networks [J]. IEEE Transactions on Wireless Communications, 2015, 14(12): 6993-7003. DOI: 10.1109/TWC.2015.2463280. [11] ZHOU Zhen-yu, DONG Mian-xiong, OTA K, WU Jun, SATO T. Energy efficiency and spectral efficiency tradeoff in device- to-device (D2D) communications [J]. IEEE Wireless Communications Letters, 2014, 3(5): 485-488. DOI: 10.1109/ LWC.2014.2337295. [12] ZHOU Zhen-yu, DONG Mian-xiong, OTA K, WANG Guo-jun, YANG L T. Energy-efficient resource allocation for D2D communications underlaying cloud-RAN-based LTE-A networks [J]. IEEE Internet of Things Journal, 2016, 3(3): 428-438. DOI: 10.1109/JIOT. 2015.2497712. [13] GUO Sheng-jie, ZHOU Xiang-wei, XIAO Sa, SUN Ming-xuan. Fairness-aware energy-efficient resource allocation in D2D communication networks [J]. IEEE Systems Journal, 2019, 13(2): 1273-1284. DOI: 10.1109/JS YST.2018.2838539. [14] ZHOU Zhen-yu, SHI Rui-feng, SATO T, LIU Zhi-heng, DONG Mian-xiong, OTA K. Game-theoretic approach to energy- efficient resource allocation in device-to-device underlay communications [J]. IET Communications, 2015, 9(3): 375-385. DOI:10.1049/iet-com.2014.0337. [15] DENG N, HAENGGI M. The energy and rate meta distributions in wirelessly powered D2D networks [J]. IEEE Journal on Selected Areas in Communications, 2019, 37(2): 269-282. DOI: 10. 1109/JSAC.2018.2872373. [16] CHANG Zheng, ZHOU Sheng, RISTANIEMI T, NIU Zhi-sheng. Collaborative mobile clouds: An energy efficient paradigm for content sharing [J]. IEEE Wireless Communications, 2018, 25(2): 186-192. DOI:10.1109/MWC.2017.1600170. [17] TAO Mei-xia, LIANG Ying-chang, ZHANG Fan. Resource allocation for delay differentiated traffic in multiuser OFDM systems [J]. IEEE Transactions on Wireless Communications, 2008, 7(6): 2190-2201. DOI:10.1109/TWC.2008.060882. [18] WANG Shao-wei, SHI Wei-jia, WANG Chong-gang. Energy- efficient resource management in OFDM-based cognitive radio networks under channel uncertainty [J]. IEEE Transactions on Communications, 2015, 63(9): 3092-3102. DOI: 10.1109/ TCOMM.2015.2452251. [19] CROUZEIX J P, FERLAND J A, SCHAIBLE S. An algorithm for generalized fractional programs [J]. Journal of Optimization Theory and Applications, 1985, 47(1): 35-49. DOI: 10.1007/ BF01582887. [20] CHANG Zheng, HOU Xin, GUO Xi-juan, RISTANIEMI T, HAN Zhu. Secure and energy-efficient resource allocation for wireless power enabled full-/half-duplex multiple-antenna relay systems [J]. IEEE Transactions on Vehicular Technology, 2017, 66(12): 11208-11219. DOI:10.1109/TVT.2017.273 3040. [21] CHANG Zheng, GONG Jie, LI Ying-yu, ZHOU Zhen-yu, RISTANIENI Tapani, SHI Guang-ming, HAN Zhu, NIU Zhi-sheng. Energy efficient resource allocation for wireless power transfer enabled collaborative mobile clouds [J]. IEEE Journal on Selected Areas in Communications, 2016, 34(12): 3438-3450. DOI: 10.1109/ JSAC.2016.2611843. [22] CHANG Zheng, GONG Jie, RISTANIEMI T, NIU Zhi-sheng. Energy-efficient resource allocation and user scheduling for collaborative mobile clouds with hybrid receivers [J]. IEEE Transactions on Vehicular Technology, 2016, 65(12): 9834-9846. DOI:10.1109/TVT.2016.2525821. [23] CHEN H J, SCHAIBLE S, SHEU R L. Generic algorithm for generalized fractional programming [J]. Journal of Optimization Theory and Applications, 2009, 141(1): 93-105. DOI: 10.1007/ s10957-008-9499-7. [24] BOYD S, VANDENBERGHE L. Convex optimization [M]. Cambridge: Cambridge University Press, 2004. DOI: 10.1017/ cbo9780511804441. [25] TUY H. Convex analysis and global optimization [M]. Boston, MA: Springer US, 1998. DOI: 10.1007/978-1-4757-2809-5. [26] BOYD S. Sequential convex programming [EB/OL][1998-10-04] http://stanford.edu/class/ee364b/lectures/ seq.slides.pdf. [27] LI Yu-zhou, SHENG Min, WANG Xi-jun, ZHANG Yan, WEN Juan. Max–min energy-efficient power allocation in interference-limited wireless networks [J]. IEEE Transactions on Vehicular Technology, 2015, 64(9): 4321-4326. DOI: 10.1109/ TVT.2014.2361920. [28] WU Xiao-lu, CHEN Yue-yun, YUAN Xiao-pan, MKIRAMWENI M E. Joint resource allocation and power control for cellular and device-to-device multicast based on cognitive radio [J]. IET Communications, 2014, 8(16): 2805-2813. DOI:10.1049/iet-com.2013.1041. [29] NGUYEN T D, HAN Y. A proportional fairness algorithm with QoS provision in downlink OFDMA systems [J]. IEEE Communications Letters, 2006, 10(11): 760-762. DOI: 10.1109/LCOMM.2006.060750. (Edited by ZHENG Yu-tong) 中文导读 D2D组播通信中的高能效资源分配研究 摘要:研究了D2D组播通信中的资源分配问题,为了获得公平的能量效率,采用最大最小公平准则作为优化准则,以D2D组播的能量效率作为优化目标函数,在考虑最大发射功率约束和最小速率约束的情况下,通过最大化最小D2D组播的能量效率来实现公平的资源分配,并将上述优化问题建模为非凸的、混合整数规划问题。提出了一种次优的资源分配算法来求解上述问题。首先,采用提出的信道分配算法将信道资源分配给不同的D2D组播用户。然后,对于给定的信道分配,提出了两种迭代的功率分配算法。仿真实验结果证明了提出算法的收敛性。另外,与传统的吞吐量最大化算法进行了比较,实验结果表明提出的算法能够提高系统的能量效率,并且保证不同D2D组播之间的公平性。 关键词:D2D;能量效率;资源分配;最大最小公平规则;分式规划 Foundation item: Projects(61801237, 61701255) supported by the National Natural Science Foundation of China; Project(SBH17024) supported by the Postdoctoral Science Foundation of Jiangsu Province, China; Project(15KJB510026) supported by the Natural Science Foundation of the Jiangsu Higher Education Institutions, China; Project(BK20150866) supported by the Natural Science Foundation of Jiangsu Province, China; Projects(NY215046, NY217056) supported by the Introduction of Talent Fund of Nanjing University of Posts and Telecommunications, China Received date: 2018-08-28; Accepted date: 2019-03-07 Corresponding author: ZUO Jia-kuo, PhD, Lecturer; Tel: +86-15380410922; E-mail: zuojiakuo@njupt.edu.cn; ORCID: 0000-0001- 5940-7559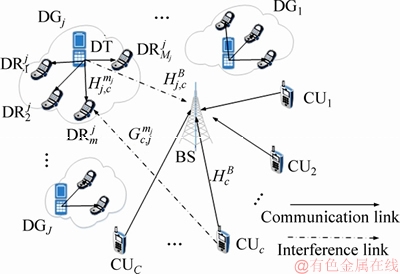
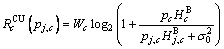 (1)
(1) is the channel gain from CUc to the BS; pj,c is the power of DT in DGj on the c-th channel;
is the channel gain from CUc to the BS; pj,c is the power of DT in DGj on the c-th channel;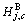 is the channel gain from DT in DGj to the BS on the c-th channel;
is the channel gain from DT in DGj to the BS on the c-th channel;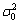 is the variance of the independent zero-mean additive white Gaussian noise (AWGN).
is the variance of the independent zero-mean additive white Gaussian noise (AWGN).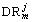 denote the m-th DR in the j-th DMG. Introduce a new parameter
denote the m-th DR in the j-th DMG. Introduce a new parameter to evaluate the quality of channel link, and then
to evaluate the quality of channel link, and then can be defined as:
can be defined as: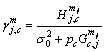 (2)
(2)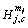 is the channel gain of DT to
is the channel gain of DT to 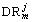 in DGj on the c-th channel;
in DGj on the c-th channel; 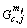 is the channel gain of the c-th CU to
is the channel gain of the c-th CU to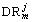 in DGj.
in DGj.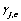 denote the weakest link in the j-th DMG, and then
denote the weakest link in the j-th DMG, and then 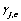 is expressed as:
is expressed as: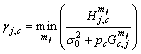 (3)
(3)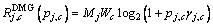 (4)
(4)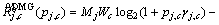
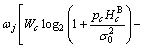
 (5)
(5)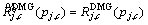 . Therefore, the definition in Eq. (5) is more general.
. Therefore, the definition in Eq. (5) is more general. indicate whether or not the c-th channel is reused by the j-th DMG. Accordingly, the EE of the j-th DMG is defined as:
indicate whether or not the c-th channel is reused by the j-th DMG. Accordingly, the EE of the j-th DMG is defined as: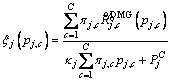 (6)
(6)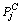 is the fixed circuit power consumption.
is the fixed circuit power consumption.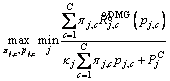
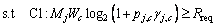
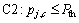


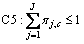 (7)
(7)
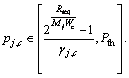 Set that the maximum transmit power for DT in the j-th DMG on the c-th channel is
Set that the maximum transmit power for DT in the j-th DMG on the c-th channel is 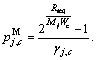 Let
Let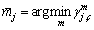 be the worst DR in the j-th DMG. Observe that channel should be allocated to DMG with low
be the worst DR in the j-th DMG. Observe that channel should be allocated to DMG with low 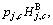 since it will introduce less interference to the CU. Therefore, define a new statistic
since it will introduce less interference to the CU. Therefore, define a new statistic Allocating channels according to
Allocating channels according to  considers not only the D2D link channel condition but also the interference channel condition.
considers not only the D2D link channel condition but also the interference channel condition.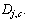 In the second step, the DMG with the lowest energy efficiency has a priority to choose the channel with the highest value
In the second step, the DMG with the lowest energy efficiency has a priority to choose the channel with the highest value 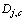 . If the energy efficiency can be improved by the new channel, then assign it to the DMG. This step is repeated until all channels are consumed. Although the proposed heuristic channel assignment algorithm is suboptimal, it has a lower complexity than the optimal channel allocation algorithm [17]. The complexity of the proposed channel assignment algorithm is approximately linear to the number of the channels, i.e. o(C) [18].
. If the energy efficiency can be improved by the new channel, then assign it to the DMG. This step is repeated until all channels are consumed. Although the proposed heuristic channel assignment algorithm is suboptimal, it has a lower complexity than the optimal channel allocation algorithm [17]. The complexity of the proposed channel assignment algorithm is approximately linear to the number of the channels, i.e. o(C) [18].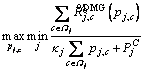
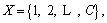
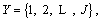
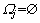
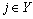
 according to
according to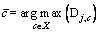
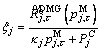
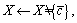

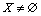
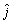 according to
according to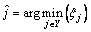
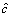 according to
according to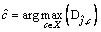

 and
and 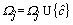
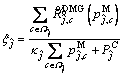
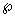 and p denote the feasible region and variable vector of Eq. (8). Introduce a new variable λ and define a new function F(λ):
and p denote the feasible region and variable vector of Eq. (8). Introduce a new variable λ and define a new function F(λ):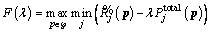 (9)
(9)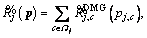
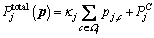 , and F(λ) is a function of variable λ. The objective function in Eq. (9) is a subtractive form of the objective function in Eq. (8).
, and F(λ) is a function of variable λ. The objective function in Eq. (9) is a subtractive form of the objective function in Eq. (8).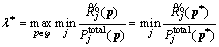 (10)
(10)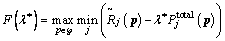
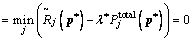 (11)
(11) (12)
(12)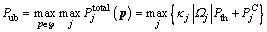 (13)
(13)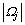 is the number of elements in Ωj.
is the number of elements in Ωj.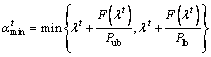 (14)
(14)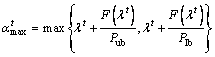 (15)
(15)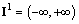
 and set termination precise ε>0
and set termination precise ε>0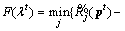
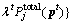
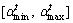 with Eqs. (14) and (15)
with Eqs. (14) and (15)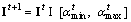 and choose
and choose 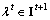
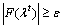
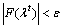
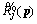 is concave on p, where
is concave on p, where 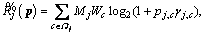 and the objective function of Eq. (9) is concave. Introduce a new variable η, and transform the nonsmooth problem in Eq. (9) to a smooth one:
and the objective function of Eq. (9) is concave. Introduce a new variable η, and transform the nonsmooth problem in Eq. (9) to a smooth one: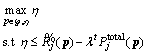 (16)
(16) is defined as Eq. (5), and Eq. (9) is non-convex and NP-hard, which is hard to find the global optimal solution. However, there is a special structure in Eq. (9). First, define two new functions φj(p) and fj(p) respectively:
is defined as Eq. (5), and Eq. (9) is non-convex and NP-hard, which is hard to find the global optimal solution. However, there is a special structure in Eq. (9). First, define two new functions φj(p) and fj(p) respectively: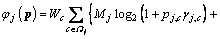
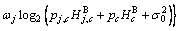 (17)
(17)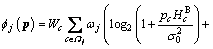
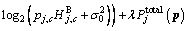 (18)
(18)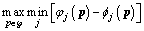 (19)
(19)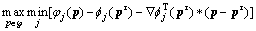 (20)
(20)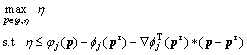 (21)
(21)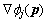 is the gradient of fj(p) at p and the element of
is the gradient of fj(p) at p and the element of 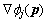 is easily given by:
is easily given by: (22)
(22)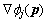 ’s element, 1≤n≤J*C.
’s element, 1≤n≤J*C.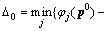
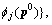 set τ=0
set τ=0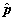
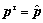
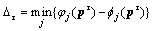

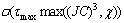 [27], where τmax is the maximum iteration number of Algorithm 3. Therefore, the total computational complexity of the algorithm with loss of CUs’rate is
[27], where τmax is the maximum iteration number of Algorithm 3. Therefore, the total computational complexity of the algorithm with loss of CUs’rate is 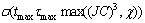 .
. and ωj=ω.
and ωj=ω. Equations (14) and (15) can be respectively rewritten as:
Equations (14) and (15) can be respectively rewritten as: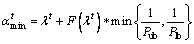 (23)
(23)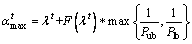 (24)
(24)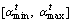 is
is 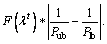 Therefore, the size of interval is determined by F(λt) and
Therefore, the size of interval is determined by F(λt) and  Based on the definition of Plb and Pub, i.e. Eqs. (12) and (13), the value of
Based on the definition of Plb and Pub, i.e. Eqs. (12) and (13), the value of 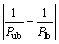 for WoL algorithm is the same as the value for WL algorithm. According to Eqs. (5) and (9), the value of F(λt) for WoL algorithm is larger than the value of F(λt) for WL algorithm. Therefore, the size of interval for WoL algorithm is larger than the size of interval for WL algorithm. More iterative times are need to find the optimal value λ* in larger size of interval. As a result, WL algorithm converges faster than WoL algorithm.
for WoL algorithm is the same as the value for WL algorithm. According to Eqs. (5) and (9), the value of F(λt) for WoL algorithm is larger than the value of F(λt) for WL algorithm. Therefore, the size of interval for WoL algorithm is larger than the size of interval for WL algorithm. More iterative times are need to find the optimal value λ* in larger size of interval. As a result, WL algorithm converges faster than WoL algorithm.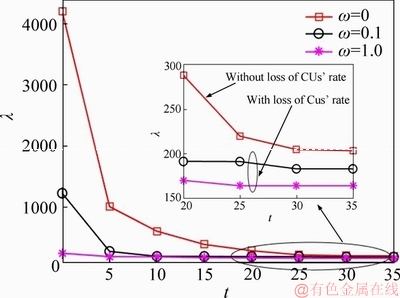
 the algorithm becomes WL algorithm. According to Eqs. (5) and (6), the EE of DMG is a monotony decrease function of weight factor ω. Therefore, the EE of the worst case DMG decreases with the growth of weight factor ω.
the algorithm becomes WL algorithm. According to Eqs. (5) and (6), the EE of DMG is a monotony decrease function of weight factor ω. Therefore, the EE of the worst case DMG decreases with the growth of weight factor ω.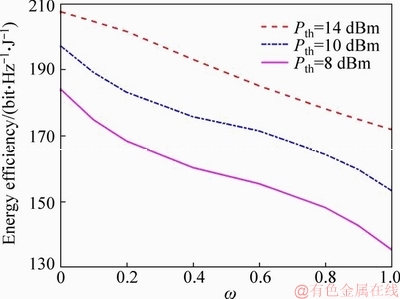
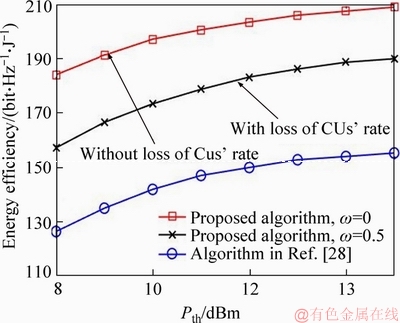
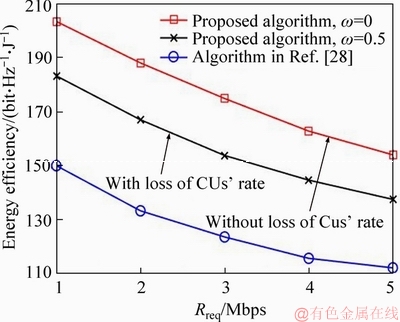

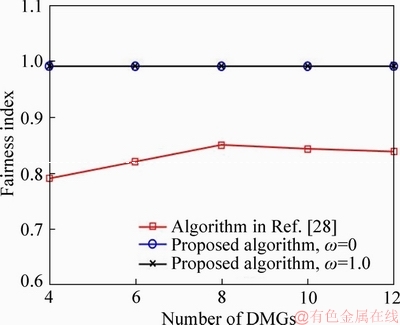
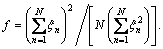 Figure 8 shows the fairness index with respect to the number of DMG with Pth=12 dBm and Rreq=1 Mbps. Obviously, fairness index performance of the proposed algorithms is better than that of the algorithm in Ref. [28]. This is because the proposed algorithms use the max-min fairness criterion as the optimization criterion, which can guarantee the fairness of resource allocation. However, the algorithm in Ref. [28] aims to maximize the total EE of the system, and more resource is allocated to the users with better link quality indicator.
Figure 8 shows the fairness index with respect to the number of DMG with Pth=12 dBm and Rreq=1 Mbps. Obviously, fairness index performance of the proposed algorithms is better than that of the algorithm in Ref. [28]. This is because the proposed algorithms use the max-min fairness criterion as the optimization criterion, which can guarantee the fairness of resource allocation. However, the algorithm in Ref. [28] aims to maximize the total EE of the system, and more resource is allocated to the users with better link quality indicator.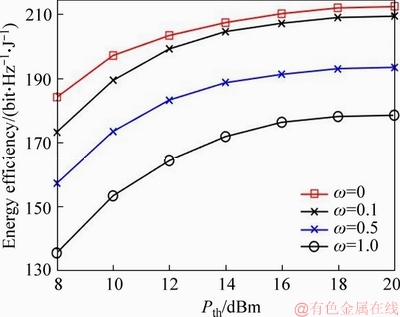
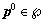 ), which makes the following inequality true:
), which makes the following inequality true: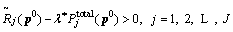 (A-1)
(A-1)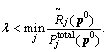 Since
Since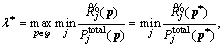 there is:
there is: 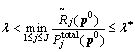 (A-2)
(A-2)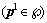 , which makes the following inequality true:
, which makes the following inequality true: (A-3)
(A-3)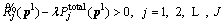 (A-4)
(A-4)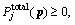 F(λ) is a monotone decreasing function on λ. Thus, there is F(λ*)≤0.
F(λ) is a monotone decreasing function on λ. Thus, there is F(λ*)≤0. 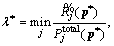 which can be rewritten as following form:
which can be rewritten as following form: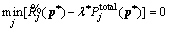 (A-5)
(A-5)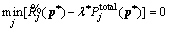 (A-6)
(A-6)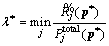 (A-7)
(A-7)

