文章编号:1004-0609(2016)-09-2042-07
西门子法钟罩炉内三氯氢硅氢还原CVD宏观动力学模型
吴 永
(银川能源学院,银川 750105)
摘 要:在已导出西门子法三氯氢硅氢还原生成Si-CVD过程本征动力学模型基础上,结合钟罩还原炉内气相物料的基本流动特征和传递-反应-CVD过程,采用反应工程学经典方法,对关键组分在圆柱状硅芯表面CVD层的浓度分布进行分析,导出浓度分布微分方程(零阶贝塞尔方程)和积分方程(零阶贝塞尔函数),建立了Si的沉积速率模型,即考虑CVD层浓度分布时的平均沉积厚度模型和沉积质量模型,忽略CVD层浓度分布时的平均沉积厚度简化模型和沉积质量简化模型。
关键词:反应工程;多晶硅;西门子法;三氯氢硅氢还原反应;化学气相沉积;宏观动力学模型
中图分类号:TQ013.2;O613.72 文献标志码:A
多晶硅(EG)是电子信息产业的关键基础材料,具有极其重要的战略地位;多晶硅(SG)又是太阳能光伏产业的关键基础材料,是具有重要战略地位的新能源材料。改良西门子法是当今生产高纯多晶硅的主流技术。我国的多晶硅产业起步虽晚,但发展快,生产工艺主要系引进加吸收的改良西门子法,到2009年多晶硅产能已达146 750 t/a,成为多晶硅生产大国,其中,太阳能电池产量2007年已达821 MW,居世界第二,仅次于日本(920 MW)[1-2]。多年来,高纯硅生产技术一直被欧美日等发达国家垄断,对我国实行技术封锁,故虽有引进的生产技术与装备,但并非当今先进水平[2-5]。还由于企业及行业快速发展过程中存在的诸多问题,加上2012年以来欧美国家联手对我国多晶硅太阳能产品实行制裁,致使一些企业处境困难,有的破产,有的企业至今仍未走出困境。因此,加强多晶硅生产技术和相关理论研究,加速专业人才培养、促进产业技术进步至关重要。2010年7月,教育部颁发了《同意设置的高等学校战略性新兴产业相关本科新专业名单》,其中如微电子材料、新能源材料等多个专业都涉及到硅材料技术。此举对硅材料方面的人才培养和技术进步必将发挥重要推动作用。
有关西门子法钟罩炉内三氯氢硅(SiHCl3,即三氯甲硅烷)氢还原生成Si-CVD过程动力学方面,国内系统理论研究滞后,资料匮乏,既不能满足专业教学的需要,又无力对企业技术进步和消化、吸收国外技术提供理论指导,不适应产业快速发展对高校专业人才培养的需要。20世纪80年代,著名冶金学家和半导体材料专家沈华生曾对Si-Cl-H三元系统的反应机理做过研究,并在半工业性装置(三对硅芯、四对硅芯还原炉)上进行过实验,对设备的设计要求及工艺条件进行了探讨,但未给出动力学模型,援引了BAWA的由流速、分压梯度、温度、硅棒直径等关联的沉积模型(回归式)[6]。近些年,还见到有关动力学数值模拟方面研究,如张攀等[7]应用流体力学软件对三氯氢硅和氢气系统中多晶硅化学气相沉积做过数值模拟;张华芹等[8]采用流体力学(CFD)软件对还原炉内的气相沉积过程进行模拟计算并绘制出硅棒形象图;段连[9]也对还原炉温度、流场、能耗做过类似模拟。YANG[10]提出CSTR模型,假定气体在反应器中充分混合;后来又出现了传递限制和反应限制模型,如FALLER和HURTLE[11]的化学反应限制模型,该模型假定硅芯棒表面的关键组分的浓度的等于通入反应器时的初始浓度,忽略了传递对CVD过程的影响。此后又提出考虑化学反应和传递过程影响的完全模型。侯彦青[12]在这方面做了大量工作,介绍了有关西门子反应器模型研究情况,评述了Coso的完全模型存在的主要缺陷,并提出了完全模型,即化学反应限制和传递过程限制模型,列出了气相守恒方程(包括线动量守恒、总质量守恒、单个物质质量守恒、能量守恒等),动力学-传递模型(包括动量传递、热量传递、化学物质的质量传递)等;做了参数计算;应用该模型研究了进料气流速度、气体组分、硅棒表面温度、进料气体温度和压强对沉积速率及生成单位质量多晶硅的能耗和硅表面HCl摩尔浓度的影响;分析研究了电加热(直流和交流)硅芯棒热传递模型。侯彦青的研究系统、全面,具有一定的价值,尤其是热力学分析部分;但其建模的核心部分第五章的5.3和5.4存在某些误区,未给出正确、明晰的宏观动力学模型。
西门子法钟罩炉内三氯氢硅氢还原过程,属于“三传一反”过程,主要矛盾是伴有质量(物料)传递和能量(电能-热能)传递的化学反应问题(由于传递-反应过程中气相流体的压力降较小,可忽略动量传递),不是空气动力学或流体力学问题。至于应用流体力学软件模拟西门子法传递-反应过程是否妥当,还需在理论上探讨,经受实践检验。
王樟茂等[13]在喷动流化床实验装置中对SiHCl3制取颗粒硅的动力学做过系统研究,包括反应动力学模型、颗粒硅生长速率模型和模型参数的确定及模型验证。尽管对其反应机理式中表面反应式和建立颗粒生长速率模型时质量衡算式简化处理尚存看法,但采用反应工程的经典方法,对研究西门子法三氯氢硅氢还原动力学模型亦有借鉴价值。
本文作者在已研究了该反应体系本征动力学方 程[14]的基础上,联系钟罩还原炉系统的结构和实际生产过程,抓住反应流体流动-反应的主要特征,在合理简化的基础上,用反应工程学经典方法,导出了三氯氢硅氢还原生成Si-CVD过程的宏观动力学数学模型。
1 西门子法三氯氢硅氢还原生成Si-CVD过程的本征速率方程
通过对该反应体系化学反应的热力学综合分析(包括反应耦合分析)比较认为[14],西门子反应体系生成Si-CVD的主反应,是包含通常所说的主反应SiHCl3(g)+H2(g)=Si(s)+3HCl(g)和考虑了几组耦合为反应方程式同该反应且有强化效果的耦合反应在内表观主反应;还应考虑SiHCl3的两个热分解反应,即影响三氯氢硅氢还原生成Si-CVD的主要反应应当是如下平行反应:
SiHCl3(g)+H2(g)=Si(s)+3HCl(g) (1)
2SiHCl3(g)=Si(s)+SiCl4(g)+2HCl(g) (2)
4SiHCl3(g)=Si(s)+3SiCl4(g)+2H2(g) (3)
在此基础上借助非均相气-固相催化反应模型方法,导出本征速率方程(采用浓度型):
 [mol/(m2·s)] (4)
[mol/(m2·s)] (4)
式中:ksc1、ksc2、ksc3分别为反应(1)、(2)、(3)的浓度型面积基准速率常数,ksc1:[m/s];ksc2:[m4/(mol·s)];ksc3:[m10/(mol3·s)]。
为了便于求解三氯氢硅氢还原CVD过程宏观动力学模型,对上述非线性速率方程作线性化变换(在cA=cA+0处做泰勒级数展开,略去二阶以上项)为拟一级不可逆反应型速率方程:
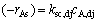 (5)
(5)
式中:等价速率常数  ;关键组分的等价浓度
;关键组分的等价浓度 。
。
为方便计,略去“dj”下标,这样,浓度型面积基准速率为
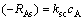 [mol/(m2·s)][14] (6)
[mol/(m2·s)][14] (6)
2 西门子法三氯氢硅氢还原过程CVD层浓度分布方程
2.1 钟罩还原炉内物料流动-反应-CVD状况(物理模型)分析
国内反应工程学权威、浙江大学教授陈甘棠先生一再强调:“建立数学模型的要诀,并不在于无所不包地把各种因素都考虑和罗列进去,这不仅会使问题复杂化而得不到解决,而且也是不必要的。恰恰相反,应当努力作出尽可能合理的简化,使之易于求解而又符合实际。当然要能正确做出这种简化,需要对过程实质有深切的认识”[15]。建立本模型亦应遵循此思想原则。
西门子法还原反应及化学气相沉积(CVD)是在钟罩式还原炉中进行。炉罩还原炉主要由底盘系统,兼做CVD基体和电热体的硅芯-电极系统,炉罩(形如古代铸钟)系统以及配套的辅助装置与控制系统组成。用于CVD基体的硅芯是由高纯硅细棒(d 8~10 mm,高约2000 mm)两长竖、一短横构装成形如拉高的“Π”架装在底盘电极座上,通过电极形成回路作为发热体提供炉内反应所需的热能。还原炉的容积大小,业内一般按炉内所设硅芯数量(Nd)如12、18、24、36、48对划分。如24对硅芯工业钟罩还原炉,其底座上由外向内的3个同心圆周上依次均匀设置12、8、4对电极座,对应装有12、8、4对硅芯架,从炉膛下部看上去有似48根固定柱(架),故也有人称为固定床;在三圈硅芯间的两个同心圆周上均匀设置有进气喷嘴——外圈8个、内圈4个;底座中部设有尾气排气口,下部通过预热器后进入尾气回收系统。待一对对硅芯电极接装完毕后,将钟式炉罩通过定位螺栓扣装在还原炉底盘上,使还原炉密闭。通过硅芯电极(电热体)加热使硅芯表面及炉内温度保持在1100 ℃左右。一定配比和一定流速与压力的原料气流经套层预热器被排出的高温尾气预热后,经环形分配管到分布均匀的各进气喷嘴进入硅棒“林立”的钟罩炉内,新鲜气体物料很快与原有气体混合;连续流动-混合的主气流到达钟罩穹顶后改变流向,返回途中又与原有气体及后续进入的气相物料混合,这样,炉内存在不同流向和不同年龄段物料间的返混,即存在反应组分在炉内的停留时间分布;连续流动的气相反应物在高温硅芯表面不断进行反应CVD,使一对对硅芯不断长粗,而反应尾气亦连续不断从钟罩炉底盘中部排气口经预热器进入回收系统。整体上看,钟罩炉内气相流体物料返混比较充分,温度、浓度均一,且与出口处尾气温度、浓度相同;属于连续、定态过程,具有全混流的基本特征,故可按全混流反应系统对待。
随着反应CVD的进行,Si(s)在硅芯表面不断沉积,细尺寸硅芯不断长粗,反应沉积表面也随之增大。因此,原料气的输入量(v0)也须相应增大以满足反应需要;另一方面,因硅芯不断长粗使钟罩炉内的有效空间VR减小,平均停留时间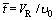 亦减小,但考虑到还原炉一个生产周期一般须4~6 d,而硅芯/棒表面Si的平均沉积速率约为1.0~1.2 mm/h,故在某一反应时段内平均停留时间
亦减小,但考虑到还原炉一个生产周期一般须4~6 d,而硅芯/棒表面Si的平均沉积速率约为1.0~1.2 mm/h,故在某一反应时段内平均停留时间 (或空时
(或空时 )可视为常数。
)可视为常数。
随着高温硅芯表面还原反应,Si在基体硅芯表面沉积形成新生固相层(简称CVD层),该固相外表面被全混流态的高温气体SiHCl3和H2(过量)以及反应生成的气体如HCl(g)和SiCl4(g)等所包围,在气相层和新生固相层间不断进行着扩散(传递,g)-吸附(g) -反应-沉积(s) -扩散(传递,g),而不断进行的CVD使新生固相层不断累积、更新,使一对对硅芯棒的外径随之长粗,直至达到目标尺寸后停炉、赶气、降温后吊起炉罩取出硅棒,清理干净后再装入新的硅芯进行下一轮生产。
综观炉内的传递-反应-CVD过程,在CVD层存在着反应组分和反应产物的浓度分布。
2.2 CVD层的浓度分布的微分方程和积分方程
该反应CVD过程可用类似气相组分在圆柱形固体催化剂上进行的气固相催化反应来处理。设钟罩还原炉进气口处原料气中关键组分A(SiHCl3)的浓度为cA0,即cAin;炉内混合气主体气流中关键组分A的浓度记作cAA,即新生CVD层外表面A的浓度,可视为炉内全混流态的A的浓度,亦即反应器出口处尾气中A的浓度cAout;CVD层内A的浓度记作cAc(r)即cAc(见图1,取其中一段微元壳体)。H2因配比较大过量,故还原炉内H2的浓度可视作恒量,炉内反应气体压力可视作恒压。此时,反应速率方程为
 (7)
(7)
将还原炉内反应气体视作全混流,在等温、等压、恒容反应情况下,cAA可表作
 (8)
(8)
式中:τ为空时,s;kv系体积基准速率常数,s-1;as为单位反应体积外表面积(亦称比外表面积,亦用av,Sv),m-1。
假定还原炉内装有N根初始半径为r0的硅芯(N=2Nd,即硅芯对数的2倍);L为每根硅芯折合圆柱体高度,m。在CVD层应用微元衡算法[15](图1所示控制体积)对A作质量(mol)衡算,定常态下:输入-输出-反应消耗=0,即
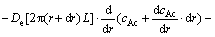
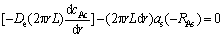 (9)
(9)
假定有效扩散系数De为常量,将速率方程(7)代入式(9),整理,略去含(dr)2的项,得
 ,(
,(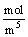 ),(
),(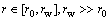 ) (10)
) (10)
边界条件为 r=rw,cAc=cAA;r=r0,dcAc/dr=0。其中rw为反应终了硅棒平均半径。
对式(10)作量纲为一化处理:设b=r0/rw,令 (
( ),
),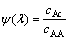 ,因cAA既是CVD层外表面
,因cAA既是CVD层外表面
的浓度,自然也是硅芯棒空间的浓度,应等于炉内全混流组分A(SiHCl3)的浓度,亦即出口尾气中A的浓度(记作cAout)。则式(10)的量纲为一方程为
 (11)
(11)
设Thiele模数 ,式(11)即为
,式(11)即为

图1 CVD层质量衡算示意图
Fig. 1 CVD layer mass balance diagram
 ,再令
,再令 ,有
,有 ,则
,则
 (12)
(12)
定解条件为 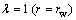 亦即
亦即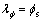 时,
时,
 (13)
(13)
 即
即 ,
,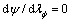 (14)
(14)
式(12)即气固相扩散-反应-沉积层即CVD层浓度分布的微分方程,系零阶贝塞尔方程[16-17]。
零阶贝塞尔方程只有一个特解即零阶贝塞尔函数设为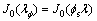 ,即硅芯表面CVD层浓度分布的积分方程,可直接写作
,即硅芯表面CVD层浓度分布的积分方程,可直接写作
 (C为积分常数) (15)
(C为积分常数) (15)
由式(13)得  ,则
,则
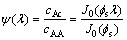 (16)
(16)
联系式(8),有
 (17)
(17)
式(17)即硅芯表面气固相扩散-反应-沉积层即CVD层内组分A的浓度分布的积分方程。
3 硅芯表面CVD沉积速度数学模型
3.1 CVD过程质量衡算方程及沉积厚度方程
在单位时间内,硅芯棒外表面(r→r+dr微元体积,见图1)因Si的CVD使硅芯体积增长量折合为质量增量,应等于同时间、同表面反应生成Si的量(总反应按简化的拟一级不可逆反应对待、并假定 ),即
),即
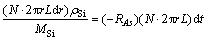 ,mol (18)
,mol (18)
式中:ρSi,MSi 分别为Si(s)的密度和摩尔质量;N=2Nd即硅芯对数的2倍,L为硅芯柱折合圆柱体高。则硅芯表面Si沉积厚度的微分方程为
 ,m (19)
,m (19)
3.2 考虑CVD层的浓度分布时硅芯基体表面沉积厚度模型
在式(19)的基础上,利用内扩散有效因子η关联可求得硅芯基体上CVD沉积厚度模型[18-19]。
内扩散有效因子η即实际反应速率与CVD层温度和浓度等于硅芯外表面温度和浓度(cAA)时的反应速率之比:
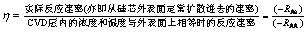
则有 ,联系式(8),有
,联系式(8),有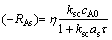 ,代入式(19),并令
,代入式(19),并令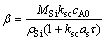 ,m/s(下同),则式(19)即
,m/s(下同),则式(19)即
 (20)
(20)
积分(t=0,r=r0),得平均沉积厚度模型
 ,m (21)
,m (21)
式(21)即用有效因子η关联的沉积厚度模型。其中,内扩散效率因子
 ,
,
( 为扩散通量) (22)
为扩散通量) (22)
由于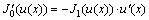 ,由式(17)有
,由式(17)有 ,则有
,则有 ,代入式(22),得
,代入式(22),得
 ,或
,或 (23)
(23)
也可求得用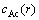 关联的沉积厚度模型。
关联的沉积厚度模型。
3.3 忽略CVD层浓度分布时的沉积厚度模型
考虑到SiHCl3的转化率低,Si的CVD过程的沉积速率约为10~20 μm/min(据几家从德国引进改良西门子法全套技术与设备的厂家,24对硅芯和12对硅芯的还原炉正常生产状态下,硅芯棒表面Si的平均沉积速率约为1.0~1.2 mm/h),即CVD层实际上是极薄的,故也可忽略CVD层内扩散影响,即可忽略CVD层的浓度分布,此时η=1,cAc=cAA=cAout=cA,则硅芯表面Si沉积厚度微分方程 (20)变为
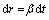 (24)
(24)
积分(t=0,r=r0)可得平均沉积厚度模型
 (或
(或 ),m (25)
),m (25)
即硅芯棒直径长大速度模型(简化模型),平均沉积厚度与关键组分的浓度及反应时间成正比。
3.4 CVD层沉积质量模型
平均沉积速度也可采用沉积Si的质量(M(r))模型。将质量衡算方程(18)稍加变化,即
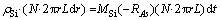 ,kg;
,kg;
而
 (26)
(26)
对式(26)积分(r0→r,M0→M),有
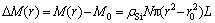 (27)
(27)
式(27)适用于考虑和忽略CVD层浓度分布两种情况,将式(21)或式(25)代入即可得相应的M(t)模型:如将式(25)代入式(27)得平均沉积质量简化模型
 (28)
(28)
将式(21)代入即为考虑CVD层浓度分布时平均沉积质量模型
 (29)
(29)
式(27)~(29)的物理意义一目了然:一定反应时间段内Si的沉积量即质量增量等于CVD层体积×硅的密度ρSi(CVD新生层形如圆套管,横截面为圆环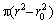 (高为L,厚Δr,N根))。
(高为L,厚Δr,N根))。
考虑到测定质量M~t数据一般比测定直(半)径r~t数据要方便且准确性相对高,故平均沉积质量简化式(28)用于生产和实验测定更为方便实用。
钟罩还原炉采用圆柱形硅芯技术已很成熟,为了提高Si的沉积速率,在满足硅芯强度与制作成本等前提下,选择侧面积大的柱体有利于增大沉积量。如等体积、等高的正四棱柱(即方柱,截面为正方形)较圆柱的侧面积大( ,则
,则 ,
, ),即采用方柱硅芯,至少在还原-沉积前期约1/4~1/3时段内Si的沉积量要大于传统圆柱硅芯;在还原-CVD的后续阶段,方柱硅芯逐渐趋向圆柱形,在此阶段其总侧表面积也大于采用圆柱硅芯时对应时段的侧面积。因此,值得在工业还原炉上进行同炉、两种不同形状硅芯沉积量对比试验。
),即采用方柱硅芯,至少在还原-沉积前期约1/4~1/3时段内Si的沉积量要大于传统圆柱硅芯;在还原-CVD的后续阶段,方柱硅芯逐渐趋向圆柱形,在此阶段其总侧表面积也大于采用圆柱硅芯时对应时段的侧面积。因此,值得在工业还原炉上进行同炉、两种不同形状硅芯沉积量对比试验。
4 结论
1) 结合钟罩炉内气相物料的流动特征和传递-反应-CVD过程,按全混流气-固相表面反应导出了CVD层浓度分布的微分方程(零阶贝塞尔方程)和积分方程(零阶贝塞尔函数)。
2) 考虑CVD层浓度分布时,平均沉积厚度模型为  ,沉积质量模型为
,沉积质量模型为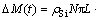
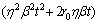 。
。
3) 忽略CVD层浓度分布时(即η=1),平均沉积厚度简化模型为  ;平均沉积质量简化模型为
;平均沉积质量简化模型为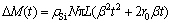 。上述模型的物理意义明晰。
。上述模型的物理意义明晰。
REFERENCES
[1] 王长贵, 王斯成.太阳能光伏发电实用技术[M]. 2版. 北京: 化学工业出版社, 2011: 1-12.
WANG Chang-gui, WANG Si-cheng. Practical technology of solar photovoltaic power generation[M]. 2nd ed. Beijing: Chemical Industry Press, 2011: 1-12.
[2] 严世权, 叶芸华. 我国改良西门子法多晶硅生产技术进展[J]. 上海有色金属, 2010, 31(4): 167-170.
YAN Shi-quan, YE Yun-hua. In our country Siemens method improvement of polysilicon production technology[J]. Shanghai Nonferrous Metals, 2010, 31(4): 167-170.
[3] 梁俊吾. 电子级多晶硅的生产工艺[J]. 中国工程科学, 2000, 2(12): 34-39.
LIANG Jun-wu. The production technology electronic grade polycrystalline silicon[J]. Engineering Science, 2000, 2(12): 34-39.
[4] 杨德仁. 太阳电池材料[M]. 北京: 化学工业出版社, 2011: 80-85.
YANG De-ren. Solar cell materials[M]. Beijing: Chemical Industry Press, 2011: 80-85.
[5] 龙桂花, 吴 彬, 韩 松, 丘克强. 太阳能级多晶硅的生产技术发展及展望[J]. 中国有色金属学报, 2008, 18(S1): s386-s392.
LONG Gui-hua, WU Bin, HAN Song, QIU Ke-qiang. Development status and prospect of solar grade silicon production technology[J]. The Chinese Journal of Nonferrous Metals, 2008, 18(S1): s386-s392.
[6] 沈华生. SiHCl3氢还原法生产超纯硅化学反应机理及工业实践经验[J]. 稀有金属, 1987, 11(6): 421-426.
SHEN Hua-sheng. Reduction of SiHCl3 hydrogen production of ultra pure silicon chemical reaction mechanism and industrial practice experience[J]. Rare Metals, 1987, 11(6): 421-426.
[7] 张 攀, 王伟文, 董海红, 吴玉雷, 陈光辉, 李建隆. 三氯氢硅和氢气系统中多晶硅化学气相沉积的数值模拟[J]. 人工晶体学, 2010, 39(2): 494-499.
ZHANG Pan, WANG Wei-wen, DONG Hai-hong, WU Yu-lei, CHEN Guang-hui, LI Jian-long. Numerical simulation of the chemical vapor deposition of polycrystalline silicon in a trichlorosilane and hydrogen system[J]. Journal of Synthetic Crystals, 2010, 39(2): 494-499.
[8] 张华芹, 茅陆荣, 周积卫, 程佳彪. 多晶硅还原炉流场的数值模拟及工艺改进[J]. 中国太阳能光伏, 2009, 7: 37-40.
ZHANG Hua-qin, MAO Lu-rong, ZHOU Ji-wei, CHENG Jia-biao. Improvement of numerical simulation and process for polysilicon reducing furnace flow field[J]. China Solar Photovoltaic, 2009, 7: 37-40.
[9] 段 连. 新型多晶硅还原炉温度, 流动和能耗的模型[D]. 天津: 天津大学, 2013: 10-52.
DUAN Lian. Simulation of temperature, flow and energy loss in a novel poly-silicon reduction furnace[D]. Tianjin: Tianjin University, 2013: 10-52.
[10] YANG Yu-bo. Transport kinetic effects in manufacture of polycrystalline silicon[D]. 1988.
[11] FALLER F, HURRLE A. High-temperature CVD for crystalline silicon thin film solar cells[J]. IEEE Transactions on Electron Devices, 1999, 46: 2048-2054.
[12] 侯彦青. 改良西门子法制备多晶硅过程的理论分析及建模[D]. 昆明: 昆明理工大学, 2013: 83-114.
HOU Yan-qing. Theoretical analysis and modeling Siemens preparation of polysilicon process improvement[D]. Kunming: Kunming University of Science and Technology, 2013: 83-114.
[13] 王樟茂, 吴兴松, 赵炳辉, 阙端麟. 在喷动流化床中应用SiHCl3制聚颗粒硅的动力学研究[J]. 浙江大学学报, 2000, 34(3): 233-238.
WANG Zhang-mao, WU Xing-song, ZHAO Bing-hui, QUE Duan-ling. Kinetic study of Si- particles prepraction from SiHCl3 in spouted-fluidized-bed[J]. Journal of Zhejing University, 2000, 34(3): 233-238.
[14] 吴 永, 王 伟, 刘晓瑞. 西门子法三氯氢硅氢还原Si-CVD本征动力学模型[J]. 中国有色金属学报, 2016, 待发表.
WU Yong, WANG Wei, LIU Xiao-rui. Discussion on the method of Siemens trichlorosilane hydrogen reduction process of -CVD intrinsic kinetics model[J]. The Chinese Journal of Nonferrous Metals, 2016, In press.
[15] 陈甘棠. 化学反应工程[M]. 3版. 北京: 化学工业出版社, 2007: 117-144.
CHEN Gan-tang. Chemical reaction engineering[M]. 3rd ed. Beijing: Chemical Industry Press, 2007: 117-144.
[16] 李绍芬. 反应工程[M]. 3版. 北京: 化学工业出版社, 2013: 174-176.
LI Shao-fen. Reaction engineering[M]. 3rd ed. Beijing: Chemical Industry Press, 2013: 174-176.
[17] 《数学手册》编写组. 数学手册[M]. 北京: 高等教育出版社, 1979: 1326-1333.
Compiling Group of Handbook of Gathematics. Handbook of mathematics[M]. Beijing: Higher Education Press, 1979: 1326-1333.
[18] H.斯科特·福格勒著. 化学反应工程[M]. 3版. 李术元,朱建华, 译. 北京: 化学工业出版社, 2005: 489-492, 605-609.
FOGLER H S. Chemical reaction engineering[M]. 3rd ed. LI Shu-yuan, ZHU Jian-hua. Beijing: Chemical Industry Press, 2005: 489-492, 605-609.
[19] FOGELER H S. Elements of chemical reaction engineering[M]. 4th ed. New York: Pearson Education Inc, 2006: 851-855.
Macrokinetics model of CVD trichlorosilane hydrogen reduction in bell-type furnace on Siemens method
WU Yong
(Yinchuan Energy Institute, Yinchuan 750105, China)
Abstract: On the basis of derived intrinsic-kinetics equation producing the Si-CVD of the hydrogen reduction reaction system of trichlorosilane in the bell furnace, the concentration distribution differential equation (the zero order Bessel equation), integral equation (the zero order Bessel function) and deposition rate model of Si were derived by combining the basic material flow characteristics of the gas phase and transferring reaction-CVD process and analyzing the concentration distribution of key component in the cylindrical silicon core CVD layer with the classical theory of reaction engineering, then the deposition rate model of Si-CVD was established. If CVD player concentration distribution is taken into consideration, the average deposition thickness model and the deposition quality model will be included. If not, the two simplified models will be included.
Key words: reaction engineering; polysilicon; Siemens method; reduction reaction of hydrogen trichlorosilane; chemical vapor deposition; macroscopic kinetics model
Foundation item: Project(2012348) supported by Advantages and Features of Ningxia Colleges and University, China; Project supported by Yinchuan Energy Research, China (2012)
Received date: 2015-03-10; Accepted date: 2016-06-06
Corresponding author: WU Yong; Tel: +86-951-8409381; E-mail: wuyong@nxu.edu.cn
(编辑 王 超)
基金项目:宁夏高等学校优势特色专业建设项目(宁教高2012348);银川能源学院科研基金资助项目(2012年度)
收稿日期:2015-03-10;修订日期:2016-06-06
通信作者:吴 永,教授;电话:0951-8409381;E-mail:wuyong@nxu.edu.cn