DOI: 10.11817/j.issn.1672-7207.2016.12.030

线性吸力下非饱和土地基临界荷载统一解

张常光¹，范文²，赵均海¹，曾开华³

(1. 长安大学 建筑工程学院，陕西 西安，710061；

2. 长安大学 地质工程与测绘学院，陕西 西安，710054；

3. 南昌工程学院 土木与建筑工程学院，江西 南昌，330099)

摘要：基于非饱和土的平面应变抗剪强度统一解，考虑基质吸力与中间主应力的共同影响，建立线性吸力分布下能适用于任意侧压力系数的非饱和土地基临界荷载统一解，并进行可比性及参数影响分析。所得临界荷载统一解可退化为众多特别是均布吸力下的已有解，具有广泛的适用性。研究结果表明：基质吸力及其分布对临界荷载的影响显著，且线性吸力下的影响不如均布吸力时明显；临界荷载的强度理论效应重要，基于Mohr-Coulomb强度准则结果的基础设计及施工理论上偏保守；对于正常和一般超固结非饱和土，按侧压力系数为1得到的临界荷载偏高；应充分考虑中间主应力效应、选择合适的侧压力系数、实测吸力及分布并采取有效措施保证其稳定存在。所得结果可为非饱和土地基承载力确定及基础优化设计提供一定的理论指导，具有广阔的工程应用前景。

关键词：非饱和土；临界荷载；吸力分布；中间主应力；侧压力系数

中图分类号：TU431；TU457.1⁺2             文献标志码：A         文章编号：1672-7207(2016)12-4190-08

Unified solution of critical load for foundation in unsaturated soils under linear suction

ZHANG Changguang¹, FAN Wen², ZHAO Junhai¹, ZENG Kaihua³

(1. School of Civil Engineering, Chang’an University, Xi’an 710061, China;

2. School of Geological Engineering and Geomatics, Chang’an University, Xi’an 710054, China;

3. Department of Civil Engineering and Architecture, Nanchang Institute of Technology, Nanchang, Jiangxi 330099, China)

Abstract: On the basis of the unified solution of shear strength for unsaturated soils in the plane strain condition, a unified solution of critical load for foundation in unsaturated soils under linear suction was derived, which took both matric suction and intermediate principal stress into account and was suitable for any lateral pressure coefficient. Comparability analysis and parametric studies were carried out. The unified solution of critical load obtained in this study can be reduced to many existing results, particularly for uniform suction, and thus has a broad applicability. The results show that the effect of matric suction and its distribution on critical load is significant, and the effect with linear suction is not as obvious as that with uniform suction; the strength theory effect for critical load is important, and the design and construction of foundation with use of Mohr-Coulomb failure criterion are theoretically conservative; for unsaturated soils under normal consolidation or general over-consolidation, the critical load with lateral pressure coefficient of 1 is higher; the intermediate principal stress effect should be fully considered and an appropriate lateral pressure coefficient is to be chosen; the matric suction and its distribution should be monitored in situ and some effective measures are adopted to ensure the stability of matric suction. This proposed result can provide a theoretical basis for the bearing capacity determination and optimization design of foundation in unsaturated soils, and therefore has a good prospect of engineering applications.

Key words: unsaturated soils; critical load; suction distributions; intermediate principal stress; lateral pressure coefficient

通常将条形地基塑性区最大开展深度Z_max等于1/4倍基础宽度B时的载荷称为临界荷载^[1]，并作为地基承载力的设计控制值。当前临界荷载主要研究的是单相弹塑性地基^[1-7]，采用Mohr-Coulomb(M-C)强度准则^[2-5]或统一强度理论^[6-7]且逐渐考虑了侧压力系数k_o不等于1的影响^[2-6]，但实际地基土多常年处于非饱和状态^[8-9]，应考虑非饱和土特性即基质吸力及其分布的重要影响。张常光等^[10-11]得到了非饱和土地基的临界荷载解析解，但只适用于常基质吸力即吸力沿深度均匀分布的情况，与地基土中真实的吸力分布相差较大。地基中基质吸力大小和分布与外部环境条件密切相关，如降雨、蒸发、植被、覆盖层等，假定基质吸力均匀分布仅适用于地下水位很深的极少数情况，而非饱和土的工程设计与施工实践表明，可取沿深度的线性减小来较准确地描述基质吸力的实际分布^[8-9]。地基土的侧压力系数k_o与超固结比R_OC密切相关^[3]，可能大于1也可能小于或等于1。另外，条形基础处于平面应变状态，则地基土的强度参数也有别于由常规轴对称压缩试验确定的参数，而与中间主应力σ₂效应有关^[12]。张常光等^{[11, 13]}建立的非饱和土平面应变抗剪强度统一解，能合理考虑中间主应力对非饱和土强度的影响，已得到初步的工程应用^[14-20]。综上可知，应考虑基质吸力及其分布、中间主应力与侧压力系数的综合影响，建立理论上符合工程土体实际特性且应用广泛的临界荷载解答。因此，本文作者基于非饱和土的平面应变抗剪强度统一解，考虑地基土体强度的非饱和特性与中间主应力效应，推导了线性吸力分布下能适用于任意侧压力系数的临界荷载统一解，对所得统一解的可比性进行分析，并得出各参数的影响特性。所得结果可为非饱和土地基承载力确定及基础优化设计提供一定的理论指导，具有广阔的工程应用前景。

1  非饱和土平面应变抗剪强度统一解

张常光等^{[11, 13]}结合统一强度理论^[12]与非饱和土Fredlund双应力状态变量抗剪强度公式^[21]，利用拓展类比方法建立的非饱和土平面应变抗剪强度统一解  τ_f为

            (1)

其中：； ；；；c′和φ′分别为非饱和土对应饱和土的有效黏聚力与有效内摩擦角；和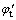分别为统一有效黏聚力与统一有效内摩擦角；c_tt为非饱和土统一总黏聚力；u_a为孔隙气压力；u_w为孔隙水压力；(u_a-u_w)为基质吸力；σ为总法向应力；(σ-u_a)为净法向应力；φ^b为与基质吸力(u_a-u_w)有关的吸力角；为统一吸力角；b为统一强度理论参数，0≤b≤1。

式(1)通过参数b反映中间主应力σ₂效应和强度准则的选取，参数b=0时，式(1)退化为不考虑中间主应力影响即基于M-C强度准则的Fredlund双应力状态变量非饱和土抗剪强度公式^[21]，参数b=1时为基于双剪应力强度准则的非饱和土抗剪强度公式，参数0＜b＜1时为一系列新的非饱和土抗剪强度公式，故应用式(1)可探讨处于平面应变状态下的基础、挡墙及边坡等各种非饱和土结构的强度理论效应。

2  线性吸力下的临界荷载统一解

2.1  基质吸力线性分布

某一非饱和土条形基础的宽度为B、埋深为D，如图1所示，地下水位D_w位于基础埋深以下一定深度。

实际工程中条形基础的埋深D一般较浅，地基土的基质吸力多处于低吸力范围，工程应用时常近似为2种情况^[8-9]：沿深度均匀分布、线性减小至地下水位D_w。当基质吸力沿深度线性减小直到地下水位D_w处为零时，设地基中M点距基底的距离为Z，则M点处的基质吸力为

      (2)

式中：(u_a-u_w)_o为地表处的基质吸力，称为地表基质吸力。

图1  地基应力及基质吸力分布

Fig. 1  Stresses of foundation and distributions of matric suction

从图1和式(2)可以看出：当地下水位D_w很深即D_w→∞时，基质吸力沿深度的变化可以忽略，将其看作是均匀分布的，也就是说基质吸力均匀分布是其线性分布的1个特例。

2.2  临界荷载统一解

均质非饱和土的重度均为γ，地基中M点距基底的距离即塑性区开展深度为Z，基底均布荷载为p，将自重应力γ(D+Z)引起的应力转换到附加应力(p-γD)对应的主应力方向上，叠加得M点的应力之和为^[2]

；

；

         (3)

式中：侧压力系数^[3]，R_OC为非饱和土的超固结比，R_OC≥1；β₀，β₁和β₂为图1中所示的夹角。

当M点达到极限平衡时，其应力式(3)满足非饱和土平面应变抗剪强度统一解式(1)，整理得

       (4)

因在基础边缘下B/4深度范围内，其塑性区应力满足(σ_z-σ_x)＞2τ_zx^[11]，进而可以利用数学近似公式^[2](当5n≥m＞n＞0时，相对误差＜7%；当m＞5m＞0时，相对误差＜5%)^[22]来简化式(4)，并将式(1)~(3)代入式(4)，整理得塑性区开展深度Z为

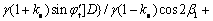
         (5)

当基础尺寸、非饱和土的性质及基质吸力大小与分布一定时，Z仅是夹角β₀和β₁的函数，可求出塑性区最大开展深度Z_max。由和得

，         (6)

将式(6)代入式(5)，整理得塑性区最大开展深度Z_max为

            (7)

将式(7)变形得条形基础的基底均布荷载p为

    (8)

式中：M_ZL、M_DL和M_CL为线性吸力下的地基承载力系数，其表达式分别为

          (9)

式(8)是按均质非饱和土地基进行推导的，若地基处于成层土中，则其第1项中的重度γ是指基础底面以下非饱和土的重度，第2项中的重度γ是指基底以上埋深范围内非饱和土的平均加权重度，用γ_D表示以示区别。令地基中塑性区最大开展深度Z_max等于基础宽度B的1/4，即Z_max=B/4，则由式(8)得非饱和土条形地基的临界荷载p_1/4统一解为

   (10)

式中：地基承载力系数M_BL=M_ZL/4。

2.3  可比性分析

1) 均布吸力下的临界荷载解析解。本文临界荷载p_1/4统一解式(10)针对基质吸力沿深度线性变化，如令地下水位D_w趋于无穷，地表基质吸力(u_a-u_w)_o即为沿深度均布时的基质吸力(u_a-u_w)，此时式(10)则变为文献[10-11]中均布吸力下的临界荷载p_1/4解析解，即

 (11)

其中，均布吸力下的地基承载力系数M_ZU、M_DU、M_CU和M_BU分别为

             (12)

因此，文献[10-11]中均布吸力下的临界荷载p_1/4解析解式(11)只是本文线性吸力下临界荷载p_1/4统一解式(10)的1个特例。另外，对比式(9)和式(12)可知：当基质吸力线性减小时，地基承载力系数M_ZL除了与基质吸力均匀分布时的侧压力系数k_o及统一有效内摩擦角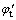有关外，还与地表基质吸力(u_a-u_w)_o、统一吸力角、非饱和土重度γ以及地下水位D_w等有关；承载力系数M_DL不再等于M_ZL+1，但承载力系数M_CL=M_CU，没有发生变化。

2) 影响因素定性分析。本文临界荷载统一解式(10)建立在平面应变非饱和土抗剪强度统一解的基础上，考虑了基质吸力(大小及线性、均匀分布)、中间主应力效应(即参数b∈[0，1])、侧压力系数k_o(即超固结比R_OC≥1)等综合影响，具有广泛的理论意义。当R_OC=1，b=0和(u_a-u_w)_o=0时，式(10)变为正常固结饱和土临界荷载的M-C强度准则解答^[2-3]；当k_o=1，b=0和(u_a-u_w)_o=0时，式(10)变为自重应力场如同静水压力时饱和土临界荷载的M-C强度准则解答^[1]；当k_o=1和(u_a-u_w)_o=0时，式(10)变为自重应力场如同静水压力时饱和土临界荷载的统一强度理论解答^[7]；当(u_a-u_w)_o=0时，式(10)变为考虑侧压力系数k_o影响的饱和土临界荷载的统一强度理论解答^[6]；当D_w→∞即(u_a-u_w)_o=(u_a-u_w)时，式(10)变为均布吸力下非饱和土临界荷载的M-C强度准则解答(b=0)及统一强度理论解答(b∈[0，1])^[10-11]。因此，本文所得临界荷载统一解式(10)具有很好的可比性，能退化为众多已有解，而且还包含很多新的解，可以适用于更多实际不同的工程情况，同时这也是对所得临界荷载统一解式(10)进行的必要性验证。

3  参数影响特性

主要探讨基质吸力、中间主应力及超固结比对地基临界荷载p_1/4的影响特性。取文献[10]中的某条形基础算例，其宽度B=4 m，埋深D=3 m，均质非饱和土的重度γ=19.5 kN/m³；对应饱和土的有效黏聚力c′=20 kPa，有效内摩擦角φ′=22°；地下水位在基底以下6 m处，即地下水位D_w=9 m；基质吸力处于低吸力范围，且吸力角φ^b=14°。在以下分析与讨论中，线性吸力下的临界荷载p_1/4由式(10)计算，均布吸力下的临界荷载p_1/4由式(11)求得，并在图中用LD(Linear Distribution)代表吸力线性分布，UD(Uniform Distribution)代表吸力均匀分布。

3.1  基质吸力

基质吸力是非饱和土的基本属性^[8-9]，若基质吸力为零，则为完全饱和土。基质吸力的影响特性包括基质吸力的大小和分布2个方面，图2给出了统一强度理论参数b为0和1、侧压力系数k_o为1-sinφ′和1时，线性与均匀2种吸力分布下正常固结土(R_OC=1)的临界荷载p_1/4与基质吸力的变化关系。

由图2可以看出：随着地表基质吸力(u_a-u_w)_o或基质吸力(u_a-u_w)的增加，不同吸力分布、相同参数b不同侧压力系数k_o以及相同侧压力系数k_o不同参数b下的临界荷载p_1/4均直线增大。对于相同参数b不同侧压力系数k_o的情况，侧压力系数k_o=1时临界荷载p_1/4明显比k_o=1-sinφ′的大，即对于正常固结非饱和土按静水自重应力场得到的临界荷载p_1/4明显偏大，基于此的基础设计将不安全；对于相同侧压力系数k_o不同参数b的情况，参数b=1时临界荷载p_1/4明显比参数b=0的大，即参数b=0由不考虑中间主应力影响的M-C强度准则得到的临界荷载p_1/4明显偏小，应考虑中间主应力对临界荷载p_1/4的提高作用，充分发挥非饱和土的强度潜能；不同参数b与不同侧压力系数k_o可能会有相同的临界荷载p_1/4，如对线性吸力分布图2(a)而言，当地表基质吸力(u_a-u_w)_o=200 kPa时，k_o=1-sinφ′且b=1的临界荷载p_1/4就与k_o=1且b=0的p_1/4相等，而在地表基质吸力(u_a-u_w)_o＞200 kPa的范围内，k_o=1-sinφ′且b=1的临界荷载p_1/4是大于k_o=1且b=0的，这表明此情况下中间主应力的增强效应已大于侧压力系数的围压提高效应，对均匀吸力分布这个相应基质吸力已减小为68 kPa。

图2  基质吸力(u_a-u_w)的影响

Fig. 2  Effect of matric suction (u_a-u_w)

对比图2(a)和图2(b)可以看出：在地表基质吸力(u_a-u_w)_o与基质吸力(u_a-u_w)均为零即完全饱和土的情况下，除线性与均匀2种吸力分布下的临界荷载p_1/4相等以外，其他同条件下线性吸力分布的临界荷载p_1/4均比均匀吸力分布的小，而且随着地表基质吸力与基质吸力的增加，2种吸力分布下临界荷载p_1/4间的差异也越来越大。当侧压力系数k_o=1-sinφ′、参数b=0时，2种吸力分布下完全饱和土的临界荷载p_1/4相等且为232.04 kPa，线性吸力下临界荷载p_1/4随地表基质吸力(u_a-u_w)_o从0 kPa增加到250 kPa，增大了125.41 kPa，即相比完全饱和时增大了54.1%，而均布吸力下临界荷载p_1/4随基质吸力(u_a-u_w)从0 kPa，增加到250 kPa，增大了376.22 kPa，即相比完全饱和时增大了162.1%，明显大于线性吸力下的增加量。若不考虑基质吸力沿深度的变化而直接按均布吸力计算，则会得到过于偏大的临界荷载p_1/4，基于此的基础设计将极其危险，应考虑基质吸力的影响并实测其具体分布，同时需采取有效工程措施来保证基质吸力的稳定存在。

3.2  中间主应力

选取不同的b即选取不同的强度准则及不同程度的中间主应力σ₂效应^[12]，参数b越大σ₂效应就越大。图3给出了(地表)基质吸力取0 kPa(完全饱和土) 和100 kPa(非饱和土)，侧压力系数k_o取1-sinφ′和1时，线性与均匀2种吸力分布下正常固结土(R_OC=1)的临界荷载p_1/4与统一强度理论参数b的变化关系。

图3  中间主应力的影响

Fig. 3  Effect of intermediate principal stress

由图3可以看出：随着参数b即中间主应力σ₂效应增加，不同吸力分布、相同(地表)基质吸力不同侧压力系数k_o以及相同侧压力系数k_o不同(地表)基质吸力下的临界荷载p_1/4均呈非线性增大。对于相同(地表)基质吸力不同侧压力系数k_o的情况，与图2中类似，侧压力系数k_o=1时临界荷载p_1/4明显比侧压力系数k_o=1-sinφ′的大；对于相同侧压力系数k_o不同(地表)基质吸力的情况，(地表)基质吸力为100 kPa时临界荷载p_1/4明显比完全饱和土的大。对于2种吸力分布下的任意参数b，都是完全饱和土在k_o=1-sinφ′时的临界荷载p_1/4最小、(地表)基质吸力为100 kPa的非饱和土在k_o=1时的临界荷载p_1/4最大；在完全饱和土即(地表)基质吸力为零、不同侧压力系数k_o下，2种吸力分布下的临界荷载p_1/4相等；但对于线性吸力分布，k_o=1时完全饱和土的临界荷载p_1/4却大于地表基质吸力为100 kPa的非饱和土在k_o=1-sinφ′时的p_1/4，即此情况下侧压力系数k_o的围压提高效应大于基质吸力的增强效应，而均布吸力时这2种效应的相对大小却与线性吸力时完全相反，这表明侧压力系数与基质吸力的影响程度及相对大小与基质吸力的分布密切相关。

另外，对比图3(a)和图3(b)可知：同条件时非饱和土均布吸力下的临界荷载p_1/4大于线性吸力的p_1/4，且不同侧压力系数k_o、不同基质吸力下的临界荷载p_1/4差异更明显，不同参数b即中间主应力σ₂效应的影响也更显著。当侧压力系数k_o为1-sinφ′和(地表)基质吸力为100 kPa时，参数b=1时临界荷载p_1/4比参数b=0时增大了116.56 kPa(线性吸力)和158.70 kPa(均布吸力)，这表明非饱和土地基临界荷载p_1/4的强度理论效应显著，考虑中间主应力能更加充分发挥非饱和土的自承载能力，保证基础设计的安全性和经济性。

3.3  超固结比

非饱和土一般为超固结土，其侧压力系数k_o可能小于等于1，也可能大于1。侧压力系数k_o可表示为超固结比R_OC的函数()，随着超固结比R_OC的增加而增大。图4给出了(地表)基质吸力取0 kPa(完全饱和土)和100 kPa(非饱和土)、统一强度理论参数b取0.5时，线性与均匀2种吸力分布下超固结土(R_OC＞1)的临界荷载p_1/4与超固结比R_OC的变化关系。

由图4可以看出：随着超固结比R_OC即侧压力系数k_o的增加，2种吸力分布下超固结非饱和土的临界荷载p_1/4均不断增大。当(地表)基质吸力=100 kPa、参数b=0.5时，R_OC=3时临界荷载p_1/4比R_OC=1(正常固结土)时增大了55.1%(线性吸力)和40.6%(均布吸力)。若不考虑超固结比R_OC的影响，直接按静水自重应力场即k_o=1计算，则完全饱和土即(地表)基质吸力为零时的临界荷载p_1/4为446.36 kPa，而(地表)基质吸力为100 kPa时非饱和土的临界荷载p_1/4为508.93 kPa(线性吸力)和634.08 kPa (均布吸力)，这3个临界荷载值均与超固结比R_OC=2.56时对应的临界荷载p_1/4相等，而超固结比R_OC＜2.56时k_o=1对应的临界荷载p_1/4明显偏大，超固结比R_OC＞2.56时k_o=1对应的临界荷载p_1/4略有偏小，这表明按静水自重应力场即k_o=1得到的临界荷载p_1/4是否合理及差异程度，与超固结比R_OC及其大小都密切相关，对于正常及一般超固结土由k_o=1得到的临界荷载p_1/4偏差较大，应选择合适的侧压力系数k_o。

图4  超固结比R_OC的影响

Fig. 4  Effect of over-consolidation ratio (R_OC)

如果不详细考虑与区分R_OC的影响，也会出现这样的情况：饱和土按k_o=1与非饱和土按k_o= 计算得到的临界荷载p_1/4相等(见图4(a))，这在一定程度上也说明了当前不考虑基质吸力按完全饱和土及k_o=1计算临界荷载p_1/4的可能性和适用性^[1]。但这种情况毕竟是极少数，如图4(b)吸力均布时就没有出现这种情况。图4(a)中只出现1次这种情况。从科学研究及最优化设计与精细化施工的角度考虑，都需要对工程土体的真实特性及所处地层环境进行机理研究，以尽量做到认识本质、降低造价和安全施工。

4  结论

1) 本文建立的线性吸力下非饱和土地基临界荷载统一解能适用于任意侧压力系数，并考虑了基质吸力和中间主应力的共同影响，可退化为众多特别是均布吸力下非饱和土的已有解，根据实际工程的地基土及地下水位等具体情况可进行合理选择，具有广泛的适用性和很好的可比性。

2) 非饱和土地基临界荷载的中间主应力效应即采用不同强度准则造成的差异显著，由不考虑中间主应力影响的Mohr-Coulomb强度准则得到的临界荷载明显偏小，基于此的非饱和土基础设计及施工易造成不必要的浪费，应考虑非饱和土强度的中间主应力效应，充分发挥非饱和土的强度潜能。

3) 基质吸力及其分布对非饱和土地基临界荷载的影响明显，且基质吸力的影响与吸力分布、侧压力系数及中间主应力效应相关，线性吸力下的影响不如均布吸力时显著，侧压力系数越大、中间主应力效应越强，基质吸力及其分布的影响就越明显，应实测吸力值及分布并采取措施保证其稳定存在。

4) 不同基质吸力大小及分布下侧压力系数即超固结比的围压提高效应不同，对于正常及一般超固结非饱和土按侧压力系数为1得到的临界荷载明显偏高，按完全饱和土及静水自重应力场得到的临界荷载也有可能与真实临界荷载相差不大，但综合考虑仍需进行机理研究，以便选择合适的侧压力系数。

参考文献：

[1] 高大钊. 土力学与基础工程[M]. 北京: 中国建筑工业出版社, 1998: 161-166.

GAO Dazhao. Soil mechanics and foundation engineering[M]. Beijing: China Architecture and Building Press, 1998: 161-166.

[2] 赵树德. 地基弹塑性承载力K≠1.0时的计算公式[J]. 西安建筑科技大学学报, 1995, 27(3): 294-298.

ZHAO Shude. Formulation of bearing capacity of subgrade with K≠1.0[J]. Journal of Xi’an University of Architecture & Technology, 1995, 27(3): 294-298.

[3] 周安楠, 姚仰平. 侧压力系数对临界荷载的影响分析[J]. 建筑结构, 2005, 35(12): 27-30.

ZHOU Annan, YAO Yangping. Analysis of the influence of lateral pressure coefficient on critical bearing capacity[J]. Building Structure, 2005, 35(12): 27-30.

[4] 梅岭, 梅国雄, 宰金珉. K₀≠1时地基弹塑性承载力的数值分析[J]. 工程力学, 2009, 26(9): 112-116.

MEI Ling, MEI Guoxiong, ZAI Jinmin. Numerical analysis of bearing capacity of subsoil with K₀≠1[J]. Engineering Mechanics, 2009, 26(9): 112-116.

[5] 陈乐意, 李镜培, 梁发云. 考虑荷载埋深与K₀变化的地基临界荷载[J]. 岩土工程学报, 2010, 32(12): 1930-1934.

CHEN Leyi, LI Jingpei, LIANG Fayun. Critical load of ground considering load embedded depth and variation of K₀[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(12): 1930-1934.

[6] 隋凤涛, 王士杰, 马建超. 新的临界荷载计算公式[J]. 河北农业大学学报, 2009, 32(5): 94-97.

SUI Fengtao, WANG Shijie, MA Jianchao. New formula of critical load of subsoil[J]. Journal of Agricultural University of Hebei, 2009, 32(5): 94-97.

[7] 范文, 林永亮, 秦玉虎. 基于统一强度理论的地基临界荷载公式[J]. 长安大学学报(地球科学版), 2003, 25(3): 48-51.

FAN Wen, LIN Yongliang, QIN Yuhu. Formula for critical load of foundation based on the unified strength theory[J]. Journal of Chang'an University (Earth Science Edition), 2003, 25(3): 48-51.

[8] FREDLUND D G, RAHARDJO H. Soil mechanics for unsaturated soils[M]. New York: John Wiley and Sons, lnc, 1993: 1-9.

[9] LU N, LIKOS W J. Unsaturated soil mechanics[M]. New York: John Wiley and Sons, lnc, 2004: 3-40.

[10] 张常光, 曾开华, 赵均海. 非饱和土临界荷载和太沙基极限承载力解析解[J]. 同济大学学报(自然科学版), 2010, 38(12): 1736-1740.

ZHANG Changguang, ZENG Kaihua, ZHAO Junhai. Analytical solutions of critical load and Terzaghi’s ultimate bearing capacity for unsaturated soil[J]. Journal of Tongji University (Natural Science), 2010, 38(12): 1736-1740.

[11] 张常光, 胡云世, 赵均海. 平面应变条件下非饱和土抗剪强度统一解及其应用[J]. 岩土工程学报, 2011, 33(1): 32-37.

ZHANG Changguang, HU Yunshi, ZHAO Junhai. Unified solution of shear strength for unsaturated soil under plane strain condition and its application[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(1): 32-37.

[12] 俞茂宏. 岩土类材料的统一强度理论及其应用[J]. 岩土工程学报, 1994, 16(2): 1-10.

YU Maohong. Unified strength theory for geomaterials and its applications[J]. Chinese Journal of Geotechnical Engineering, 1994, 16(2): 1-10.

[13] 张常光, 张庆贺, 赵均海. 非饱和土抗剪强度及土压力统一解[J]. 岩土力学, 2010, 31(6): 1871-1876.

ZHANG Changguang, ZHANG Qinghe, ZHAO Junhai. Unified solutions of shear strength and earth pressure for unsaturated soils[J]. Rock and Soil Mechanics, 2010, 31(6): 1871-1876.

[14] 张常光, 赵均海, 张冬芳. 非饱和土强度非线性及对被动土压力的影响[J]. 广西大学学报(自然科学版), 2012, 37(4): 797-802.

ZHANG Changguang, ZHAO Junhai, ZHANG Dongfang. Nonlinear strength of unsaturated soils and its influence on passive earth pressure[J]. Journal of Guangxi University (Natural Science Edition), 2012, 37(4): 797-802.

[15] 赵均海, 梁文彪, 张常光, 等. 非饱和土库仑主动土压力统一解[J]. 岩土力学, 2013, 34(3): 609-614.

ZHAO Junhai, LIANG Wenbiao, ZHANG Changguang, et al. Unified solution of Coulomb's active earth pressure for unsaturated soils[J]. Rock and Soil Mechanics, 2013, 34(3): 609-614.

[16] 张常光, 赵均海, 朱倩. 非饱和土刚性挡墙抗倾覆临界嵌固深度研究[J]. 岩石力学与工程学报, 2014, 33(11): 2360-2369.

ZHANG Changguang, ZHAO Junhai, ZHU Qian. Critical embedment depth of rigid retaining walls in foundation pit of unsaturated soils[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(11): 2360-2369.

[17] 张常光, 孙珊珊, 殷佳. 考虑中间主应力的非饱和土刚性挡墙抗倾覆稳定性[J]. 四川大学学报(工程科学版), 2014, 46(6): 44-48, 62.

ZHANG Changguang, SUN Shanshan, YIN Jia. Anti-overturning stability of a rigid retaining wall in unsaturated soils considering the intermediate principal stress[J]. Journal of Sichuan University (Engineering Science Edition), 2014, 46(6): 44-48, 62.

[18] 张常光, 李艳, 朱倩. 考虑中间主应力的非饱和土边坡安全系数新解[J]. 水利水电科技进展, 2014, 34(6): 27-30.

ZHANG Changguang, LI Yan, ZHU Qian. New safety factor of slopes in unsaturated soils by considering the intermediate principal stress effect[J]. Advances in Science and Technology of Water Resources, 2014, 34(6): 27-30.

[19] 张常光, 陈新栋, 朱东辉. 非饱和土基坑刚性挡墙抗倾覆设计与参数分析[J]. 中南大学学报(自然科学版), 2016, 47(2): 569-576.

ZHANG Changguang, CHEN Xindong, ZHU Donghui. Anti-overturning design and parametric analysis for rigid retaining wall of foundation pit in unsaturated soils[J]. Journal of Central South University (Science and Technology), 2016, 47(2): 569-576.

[20] ZHANG Changguang, CHEN Xindong, FAN Wen. Critical embedment depth of a rigid retaining wall against overturning in unsaturated soils considering intermediate principal stress and strength nonlinearity[J]. Journal of Central South University, 2016, 23(4): 944-954.

[21] FREDLUND D G, MORGENSTEM N R, WIDGER R A. The shear strength of unsaturated soils[J]. Canadian Geotechnical Journal, 1978, 15(3): 313-321.

[22] 现代工程数学手册编委会. 现代工程数学手册[M]. 武汉: 华中工学院出版社, 1985: 1163-1170.

Editorial Committee of Handbook of Modern Mathematics in Science and Engineering. Handbook of modern mathematics in science and engineering[M]. Wuhan: Huazhong Institute of Technology Press, 1985: 1163-1170.

(编辑  杨幼平)

收稿日期：2015-12-23；修回日期：2016-03-16

基金项目(Foundation item)：中国博士后科学基金资助项目(2016T90879)；陕西省自然科学基础研究计划项目(2015JM4146)；江西省自然科学基金资助项目(20142BAB206001)；江西省教育厅科学技术研究项目(GJJ151117)(Project(2016T90879) supported by the China Postdoctoral Science Foundation; Project(2015JM4146) supported by the Natural Science Foundation for Basic Research of Shaanxi Province, China;Project(20142BAB206001) supported by the Natural Science Foundation of Jiangxi Province, China; Project(GJJ151117) supported by the Science and Technology Program for Jiangxi Educational Committee, China)

通信作者：张常光，博士，副教授，从事非饱和土与地下工程的研究；E-mail：zcg1016@163.com