基于量化预腐蚀损伤分析的航空铝合金疲劳寿命预测
来源期刊:中国有色金属学报(英文版)2017年第6期
论文作者:许良 于翔 回丽 周松
文章页码:1353 - 1362
关键词:预腐蚀铝合金;腐蚀坑;裂纹扩展;寿命预测;疲劳极限
Key words:pre-corroded aluminium alloy; corrosion pit; crack propagation; life prediction; fatigue limit
摘 要:针对航空铝合金(Al-Cu-Mg),提出了一种量化预腐蚀损伤的新方法,该方法将腐蚀坑当量成半椭圆表面裂纹。通过预腐蚀试验、裂纹扩展试验和S-N疲劳试验构建了用于描述疲劳裂纹扩展(FCP)完整阶段的分析模型,并讨论了模型参数与这些疲劳试验数据的关系。基于MATLAB/GUI软件,采用数值积分方法,将当量裂纹尺寸和FCP模型用于计算疲劳寿命。结果表明:FCP模型拟合的S形曲线可以表示裂纹扩展第一阶段至第三阶段的整体变化。此外,预测曲线显示出疲劳寿命的实际变化趋势,并从中获得了疲劳极限的保守结果。因此,对于预腐蚀Al-Cu-Mg合金,尤其是光滑试样,这种新的分析方法可以估算材料的剩余寿命。
Abstract: A new method of quantitative pre-corrosion damage of aviation aluminium (Al-Cu-Mg) alloy was proposed, which regarded corrosion pits as equivalent semi-elliptical surface cracks. An analytical model was formulated to describe the entire region of fatigue crack propagation (FCP). The relationship between the model parameters and the fatigue testing data obtained in the pre-corroded experiments, crack propagation experiments and S-N fatigue experiments was discussed. The equivalent crack sizes and the FCP equation were used to calculate the fatigue life through numerical integration based on MATLAB/GUI. The results confirm that the sigmoidal curve fitted by the FCP model expresses the whole change from Region I to Region III. In addition, the predicted curves indicate the actual trend of fatigue life and the conservative result of fatigue limit. Thus, the new analytical method can estimate the residual life of pre-corroded Al-Cu-Mg alloy, especially smooth specimens.
Trans. Nonferrous Met. Soc. China 27(2017) 1353-1362
Liang XU, Xiang YU, Li HUI, Song ZHOU
Key Laboratory of Fundamental Science for National Defence of Aeronautical Digital Manufacturing Process, Shenyang Aerospace University, Shenyang 110136, China
Received 9 March 2016; accepted 9 October 2016
Abstract: A new method of quantitative pre-corrosion damage of aviation aluminium (Al-Cu-Mg) alloy was proposed, which regarded corrosion pits as equivalent semi-elliptical surface cracks. An analytical model was formulated to describe the entire region of fatigue crack propagation (FCP). The relationship between the model parameters and the fatigue testing data obtained in the pre-corroded experiments, crack propagation experiments and S-N fatigue experiments was discussed. The equivalent crack sizes and the FCP equation were used to calculate the fatigue life through numerical integration based on MATLAB/GUI. The results confirm that the sigmoidal curve fitted by the FCP model expresses the whole change from Region I to Region III. In addition, the predicted curves indicate the actual trend of fatigue life and the conservative result of fatigue limit. Thus, the new analytical method can estimate the residual life of pre-corroded Al-Cu-Mg alloy, especially smooth specimens.
Key words: pre-corroded aluminium alloy; corrosion pit; crack propagation; life prediction; fatigue limit
1 Introduction
Aluminium alloys are widely used in military and aerospace industries owing to their low density, high strength and favourable mechanical properties [1-3]. However, the material is not only subjected to fatigue loading but also affected by corrosive environment, such as salt water and/or salt fog [4-8]. The longer the service time of the structure of aircrafts has, the more serious the corrosion damage becomes. The corroded surface can easily produce corrosion pits and then lead to significant reduction of fatigue life [9,10]. Hence, corrosion is recognized as a primary aging mechanism that affects the long-term reliability, durability and integrity of aircrafts.
The corrosion damage is the critical problem to reduce original material properties and make accurate prediction of fatigue life extremely difficult. Various researchers have studied this problem from the following aspects. According to the morphology features of corrosion pits observed by SEM, their geometrical shape was reduced to an initial semi-circular or semi-elliptical surface crack [11-15]. Afterwards, using probabilistic methods, numerical techniques, FEM, etc. [10,16-18], its characteristic parameters were also identified to be the key factor determining pre-corroded damage degree, residual fatigue strength and crack propagation rate. On the other hand, new methods were proposed based on fractal dimension [19] or fracture mechanics [20-22]. Relevant analytical softwares, such as NASGRO and FLAGRO [23-27], were applied to calculating the life of specimens and structures. Nevertheless, the research of pitting corrosion [28] demonstrated that the cross- sectional shape of corrosion pits slowly changed from approximate semi-circle to elongated semi-ellipse with the increase of corrosion time. As a result, the accuracy and precision of life prediction are limited by the fixed sizes of equivalent cracks assumed in the above methods. Hence, the relationship between the quantitative technique of pre-corrosion damage and the prediction method of fatigue life has great significance in aircraft structure design and engine life assessment.
Fatigue life is generally expressed as the sum of two segments: the life of fatigue crack initiation and propagation [29-31]. Because the life of pre-corroded aluminium alloy decreases sharply under the effect of pre-corrosion damage, it is well recognized by now [15,32-34] that the crack initiation life only accounts for less than 20% of the total life. In the life predication, therefore, it is convenient to ignore this part and directly compute the crack propagation life. Based on this hypothesis, the primary innovative point is to quantify the corrosion pit as a semi-elliptical surface crack, which changes with the pre-corrosion time. In this work, the sizes of equivalent cracks were controlled by the data of short crack propagation experiment. Moreover, an entire region FCP model based on fracture mechanics was formulated to predict the fatigue life of pre-corroded aluminium alloy. The predicted results were eventually verified by comparing with the experimental data of S-N fatigue curves.
2 Experimental
2.1 Material and specimen preparation
Experimental specimens were cut out of the Al-Cu-Mg alloy. They were supplied in the form of flat bare sheets with a thickness of 2 mm. The sizes of smooth specimens, M(T) specimens and SENT specimens are provided in Fig. 1, respectively. The surface of each specimen was polished with the 600 grit sandpaper to eliminate burrs and then scrubbed by cotton ball dipped in acetone solution.

Fig. 1 Schematic diagrams of specimen sizes
2.2 Pre-corrosion experiments
According to the ASTM standard [35] and the environmental characteristics of aircraft service, the numbered specimens were alternately corroded in 3.5% NaCl solution at test temperature of (25±5) °C for 2, 24, 72, 120, 240 and 480 h, respectively. The solution was continuously cycled by a small water pump to maintain the constant concentration. The ratio of solution volume to specimen surface area was 10-30 mL/cm2. After corrosion, all surfaces of the specimens were scoured with flowing water in more than 15 min, before being wiped, blown dry by a hair-dryer, and reserved in the drying cabinet.
After corrosion for a period of time, the specimen surface becomes rough with the obvious change of its colour from light grey to dark green, as shown in Fig. 2. The depths of corrosion pits after corrosion for 2, 24, 72, 120, 240 and 480 h were measured by a 3D stereo microscope, and experimental data points and a fitted exponential curve are shown in Fig. 3. It had been shown in previous study [34] that the corrosion rate of alloys changed steadily with the increase of corrosion time, so an exponential function was proposed to express the non-linear relationship between the pre-corrosion time and the depth of corrosion pits. Its coefficients were determined by fitting the measured data based on the least square method. This equation expression is described as
a0=1.235t 0.775 (1)
where a0 is the depth of corrosion pits and t is the pre-corrosion time.

Fig. 2 Pre-corroded specimens after corrosion for 24 h (a), 240 h (b) and 480 h (c)
2.3 Long and short crack propagation experiments
In the laboratory environment, M(T) specimens and SENT specimens were used in the experiments of long and short crack propagation, respectively. After being pre-corroded for 24 h and 240 h, they were tested on a 100 kN servo-hydraulic fatigue machine with digital closed loop control in PC (MTS 810). The stress ratios (R) were 0.06 and 0.5, and the range of loading frequency was 10-70 Hz. The visual observation localization method was used to measure the crack length with a mobile optical microscope with magnification of 30. The threshold values of long crack propagation are shown in Table 1. The degree of corrosion damage has no significant effect on the long crack propagation, so the average threshold values (△Kth) at R=0.5 and 0.06 are 71.18 and 115.74 MPa·mm1/2, respectively.
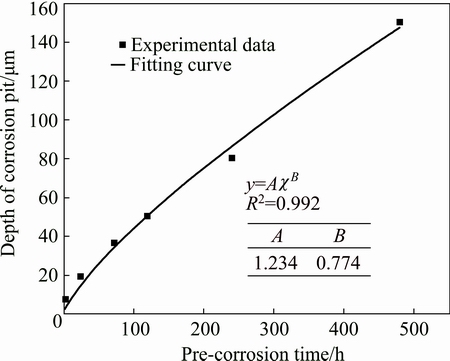
Fig. 3 Corrosion pit depth curve
Table 1 Long crack propagation threshold values

The replica method was applied to obtaining the morphology of short crack. According to the data of short crack propagation experiments, the variable a/c was fitted with the least square method to be a function of a/t. The equation of surface short cracks is given by
a/c=0.91-0.28(a/t) (2)
where a is the crack length along the direction of specimen thickness; c is the crack length along the direction of specimen width; t=B/2 is for the surface crack; B is the specimen thickness. Because the short crack initiation is the result of strain localizing in a small region within the materials [32], it is only related to material property but not to material state. This above relational expression is applicable to general specimens and pre-corroded specimens.
2.4 S-N fatigue experiments
Smooth specimens soaked in 3.5% NaCl solution for 24, 240 and 480 h were tested under constant amplitude sinusoidal cyclic loading on a high-frequency fatigue testing machine with digital closed-loop control in PC (QBG-50). The loading mode was force control with proportional error of ±1.45%. The stress ratios were 0.06 and 0.5 in the loading frequency range of 80-180 Hz. In the laboratory environment, the test temperature was (20±5) °C and the relative humidity was less than 60%.
Measured S-N curves with different pre-corrosion time are shown in Fig. 4. The grouping test method at three constant stress levels was applied in the low cycle fatigue area (104-106), which had the confidence level of more than 95%, while the test method of stress up and down was used in the high cycle fatigue area, i.e., fatigue limit (107).
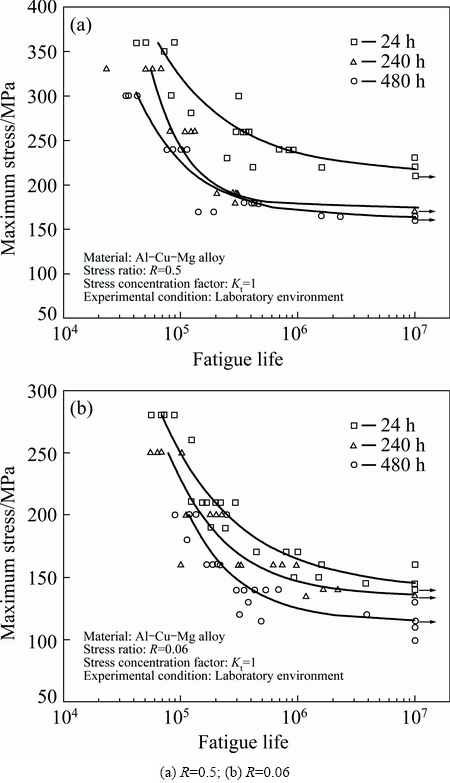
Fig. 4 S-N curves for pre-corroded smooth specimen
3 Analysis and discussion
3.1 Analysis of pre-corrosion damage
The smooth specimens pre-corroded for 24, 240 and 480 h were examined by SEM and the morphologies of fatigue fracture are shown in Fig. 5. It can be seen that the complete morphologies of surface cracks are clearly observed and an obvious notch appears within the crack source area in each image. The surface crack is similar to a semi-circle or a semi-ellipse. The notch is caused by pitting corrosion corresponding to the pre-corrosion time and the fatigue crack propagation mostly begins from the region of stress concentration at the bottom of corrosion pits. With the increase of corrosion time, the residues in corrosion pits are corroded from the state of tight adhesion to the state of loose delamination; moreover, the relatively smooth and compact wall of corrosion pits also generates rough deformation and extension in gaps and holes. In conclusion, the analysis of fatigue fracture images shows that the fatigue crack of pre-corroded Al-Cu-Mg alloy initiates at the bottom of corrosion pits and then radiates out from it.
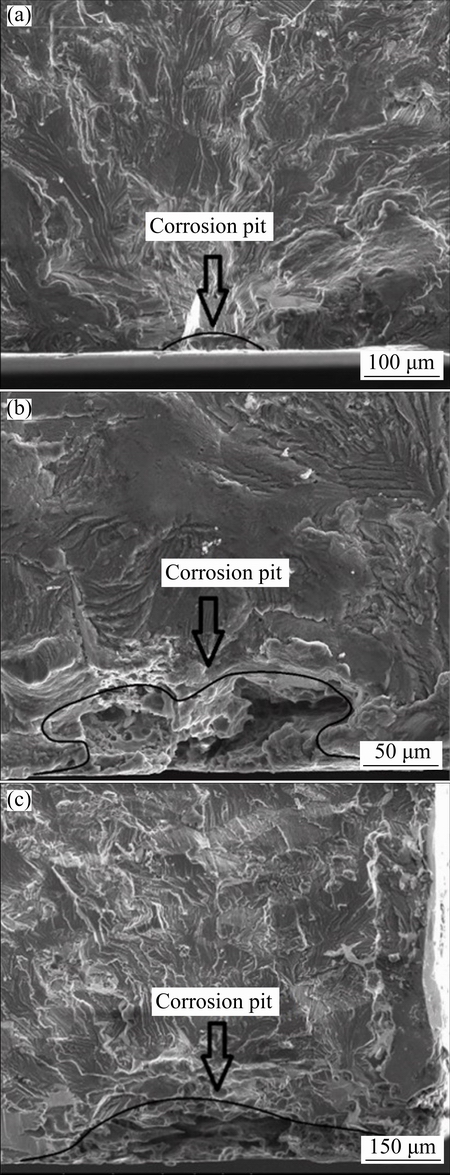
Fig. 5 Fatigue fracture images of surface crack after being pre-corroded for 24 h (a), 240 h (b) and 480 h (c)
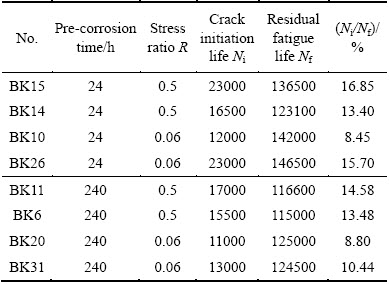
Previous studies have shown that the fatigue crack initiation life of aluminium alloy significantly declines under the condition of pre-corrosion damage and then the fatigue crack propagation life dominates the residual segment of fatigue life. If the cyclic number of external fatigue loading, which is accumulated until the appearance of a minimum crack detected distinctly, is presumed to be the crack initiation life, Table 2 shows that the crack initiation average life Ni of pre-corroded Al-Cu-Mg alloy is not only shortened but also accounts for approximately 20% of the residual fatigue life Nf. Therefore, if the prediction of fatigue life starts from the crack propagation stage, the result will also be reasonable because of pre-corrosion damage.
Table 2 Fatigue life of pre-corroded Al-Cu-Mg alloy
3.2 Quantitative analysis of corrosion pits
In practical engineering application, fatigue damage of aviation aluminium alloy is mainly caused by surface crack and the corrosion pit on pre-corroded specimen is supposed to be a surface crack for predicting the residual life of the specimen. The average depth of the maximum corrosion pits was measured by SEM, as the radius of a semi-circular surface crack. According to the principle of equivalent area, its area is transformed into that of a semi-elliptical surface crack. This process is expressed as
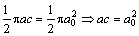 (3)
(3)
The expression of a/c in Eq. (2) obtained with the least square method is then used to derive the simultaneous equations of relationship among a, c and a0:
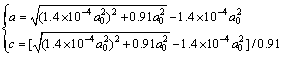 (4)
(4)
Equation (1) is plugged into Eq. (4). We have
 (5)
(5)
The relationship between the equivalent sizes (a and c) of a semi-elliptical surface crack and the pre-corrosion time is established according to Eq. (5). The fitted curve of Eq. (1) in Fig. 6 and two curves of Eq. (5) are taken on the same coordinate system and the results are shown in Fig. 6. As long as the values of a and c are considered as the radiuses of minor and major axes in the calculation of equivalent semi-elliptical surface cracks, it can be discovered by comparison that the crack growth rates along the direction of a and c are both inconsistent and their difference increases simultaneously with T. In one word, the shape of an equivalent crack starts from a semi-circle and turns into a semi-ellipse with the increase of pre-corrosion time. This change rule also accords with the actual state of corrosion pits provided in Refs. [1,2].

Fig. 6 Equivalent crack size vs pre-corrosion time
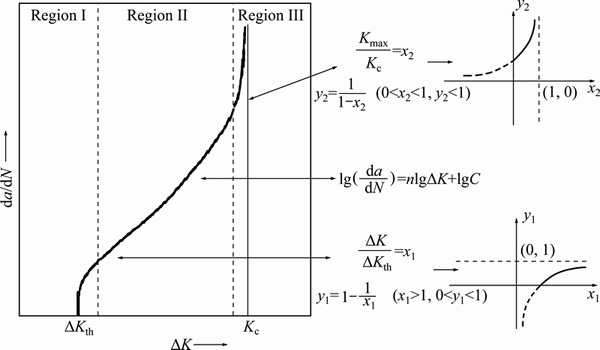
Fig. 7 Equation evolution diagram
3.3 FCP modeling of entire region
It is well-known that the entire FCP is grouped into three segments: the Region I of crack initiation and threshold value, the Region II of stable crack propagation and the Region III of unstable brittle fracture. Besides, the linear elastic fracture mechanics (LEFM) of stress field intensity approach was firstly proposed to precisely describe Region II by PARIS et al [36], who established the relationship between the FCP rate da/dN and the range of stress intensity factor ΔK at the tip of cracks subjected to cyclic stress. This equation is expressed as
da/dN=C(△K)n (6)
where C and n are the equation coefficients, respectively.
Because of the specific characteristics of FCP rate in Regions I and III, two kinds of modified inverse proportional function are derived to exactly describe the shapes of curves as
y1=1-1/x1 (x1≥1, 0≤y1<1) (7)
y2=1-1/x2 (0≤x2<1, y2>1) (8)
The definitions of x1 and x2 are
x1=△K/△Kth and x2=Kmax/Kc (9)
The threshold value ΔKth and fracture toughness Kc are the leading parameters in Regions I and III, which determine the start and end of FCP, as shown in Fig. 7. So, the two forms of ΔK/ΔKth and Kmax/Kc are used to represent the effect on ΔK in Regions I and III. Because of Kmax=ΔK/(1-R), y1 and y2 are approximately equivalent to da/dN in Regions I and III, then the Paris equation and the expression of y1 and y2 are combined together to describe the entire region of FCP. Since multiplication in the Cartesian coordinates is equal to linear addition in the double logarithmic coordinates, x1 and x2 in Eq. (9) are substituted into Eq. (7) and Eq. (8) respectively, and then the effect degrees of y1 and y2 in the FCP equation are adjusted by the increase of a weighting factor m. The formulas are derived as
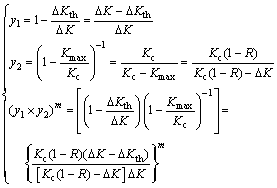 (10)
(10)
They are multiplied by the Paris equation and this function is given by
 (11)
(11)
Because the ΔK value in the denominator is eliminated with C(ΔK)n of Paris equation in the numerator, it is also given by
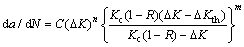 (12)
(12)
For the rapidly increasing growth exhibited in the FCP of Region III, the weighting factor m of this part, i.e., the denominator, is set to be 1, so the equation becomes
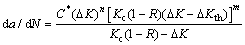 (13)
(13)
Since the Kc value in the numerator is fracture toughness of this material and (Kc)m is also a material constant, they are merged into a single parameter C*. Thus, the ultimate model to describe the entire region of FCP is shown as
 (14)
(14)
Although the models in early research, e.g., four equations of Paris, Walker, Donahue and Forman, describe different regions of FCP, none of them is used to reflect the overall trend of da/dN from Region I to Region III except the NASGRO model required more than four fitting parameters. However, massive parameters fitted by the actual experiments not only increase workload and more systemic errors but also decrease the universal applicability of model. To the entire region FCP model proposed in this paper, it retains the main advantages of the preceding models, as shown in Fig. 8, and only requires three parameters to describe different regions of FCP.

Fig. 8 Entire-region FCP modeling diagram
According to the entire region FCP model, the experimental data of pre-corroded Al-Cu-Mg alloy in Section 2.3 are used to fit curves, as shown in Fig. 9, and the model parameters are shown in Table 3, with the least square method under different stress ratios and pre-corrosion time. Although the curves change steadily in the transition stage between Regions I and II, i.e., the slope of fitted curves in this stage changes more slowly than that of experimental data, the entire region FCP model can not only capture the linear fitting effect of Region II but also coincide with the threshold value in Region I and the fracture toughness in Region III. Therefore, the sigmoidal crack propagation curve fitted by the entire region FCP model is better represented in the description of FCP.

Fig. 9 Fitted FCP curves
Table 3 Model parameters

3.4 Life prediction of pre-corroded smooth specimens
The entire region FCP model mentioned above predicts the residual fatigue life of pre-corroded material by numerical integration. Because different engineering structures have different geometrical factors, the mathematical expression of the ΔK value is derived from the stress intensity factor (SIF) handbook. The depth of equivalent surface cracks determined by Eq. (5) and pre-corrosion time T is regarded as an initial crack ai, i.e., the lower limit of numerical integration. Next, the critical crack ac calculated by fracture toughness Kc is also considered as the integral upper limit. After that, the two values are used to compute the numerical integration.
Based on MATLAB/GUI, a modular program is designed to calculate the numerical integration of Eq. (13) and predict the residual life of pre-corroded smooth specimens. It is divided into three modules containing run, clear and exit and the flowchart including different functions of each operational module is shown in Fig. 10. Because different properties and features of structures in different practical environment correspond to different parameters in the same equation, i.e., the diverse characteristics of material on pre-corrosion condition affect the values of T, C, n, m and so on in the entire region FCP model, the function of each module is independent of each other; as a result, it is convenient to reuse the same function with modified parameters. Furthermore, when material properties, model parameters and a loading array are inputted by a designed application window based on MATLAB/GUI, the corresponding predicted values including critical crack sizes, residual lives, S-N curves and parameters of their equations can be outputted after choosing and clicking “Run”. If “Clear” or “Exit” is chosen, the function of clearing any parameters or exiting this window will be achieved. The operational interface is shown in Fig. 11.

Fig. 10 MATLAB program flowchart

Fig. 11 Operation interface
The entire region FCP model implemented in MATLAB/GUI is used to predict the residual life of pre-corroded Al-Cu-Mg alloy. According to predicted parameters of S-N curve equations obtained by the above MATLAB program, the predicted S-N curves and the experimental data of pre-corroded smooth specimens in Section 2.4 with different pre-corrosion time and stress ratios are shown in Fig. 12. Although the predicted life curves deviate slightly from the experimental data in the low cycle fatigue area with pre-corrosion time of 24 h and 480 h, the predicted curves reflect the overall trend of actual fatigue life and the predicted fatigue limit is also regarded as the conservative result in material properties.
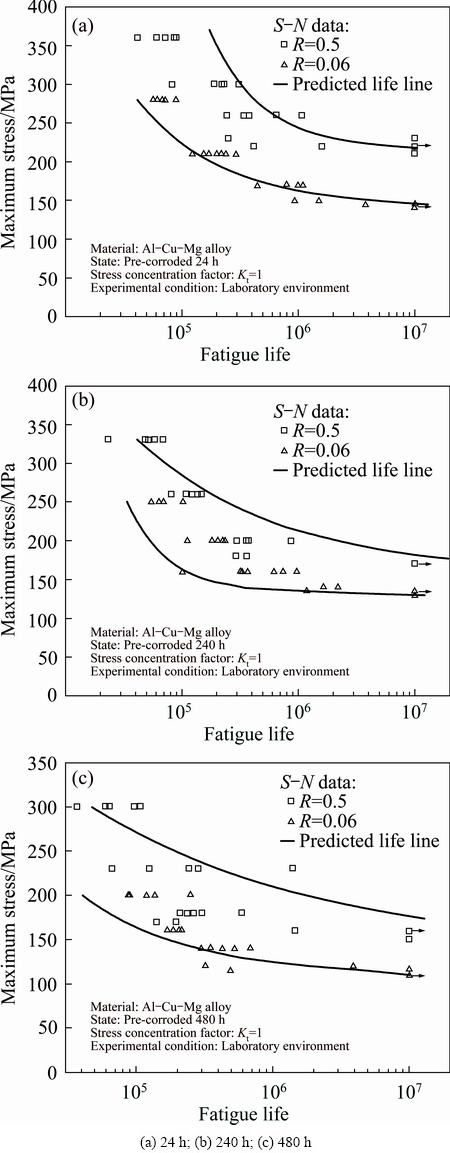
Fig. 12 Predicted S-N curves for pre-corroded smooth specimen for different time
4 Conclusions
1) To improve the accuracy of prediction, the morphology photographs of corrosion pits by SEM measurement were analyzed and it is found that the FCP of pre-corroded Al-Cu-Mg alloy mostly begins in the region of stress concentration from the bottom of the corrosion pit.
2) A simple and accurate method was proposed to predict the fatigue life of aviation aluminium alloy based on quantitative analysis of pre-corrosion damage. The corrosion pit is taken as a semi-elliptical surface crack and then the relationship between the equivalent crack sizes and pre-corrosion time T is established. Moreover, the shape of an equivalent crack starts from semi-circle and grows to semi-ellipse, which is in accordance with the actual change rule of corrosion pits.
3) On the basis of the Paris equation, an entire region FCP model is then developed to describe the crack propagation curve and predict the residual life of material. This model not only requires less fitting parameters of equations than the known models but also fits the sigmoidal curve to express the whole trend of FCP from Region I to Region III.
4) Based on MATLAB/GUI, a module program is designed to compute the numerical integration and obtain the predicted fatigue life of pre-corroded aluminium alloy. The independent operational unit is highly easier to recycle the same function after the alteration of parameters.
5) The systemic analysis of corrosion damage, including the equivalent surface crack and the entire region FCP model, is used to calculate the fatigue life of pre-corroded smooth specimens. The predicted S-N curves demonstrate that the new analytical method can better assess the pre-corroded state of material surface and build the relationship between pre-corrosion time and residual life, so the results are valuable for aircraft design and engine maintenance.
Acknowledgments
The authors would like to thank the researchers of Room No. 228 for excellent technical assistance and Engineer Lei WANG for critically reviewing the manuscript.
References
[1] WANG X, WANG J, FU C. Characterization of pitting corrosion of 7A60 aluminum alloy by EN and EIS techniques [J]. Transactions of Nonferrous Metals Society of China, 2014, 24: 3907-3916.
[2] SONG F, ZHANG X, LIU S, TAN Q, LI D. Exfoliation corrosion behavior of 7050-T6 aluminum alloy treated with various quench transfer time [J]. Transactions of Nonferrous Metals Society of China, 2014, 24: 2258-2265.
[3] LIU B, PENG C, WANG R, WANG X, LI T. Recent development and prospects for giant plane aluminum alloys [J]. The Chinese Journal of Nonferrous Metals, 2010, 20(9): 1705-1715. (in Chinese)
[4]  R, PALIN-LUC T, BATHIAS C, PARIS P C. Very high cycle fatigue of a high strength steel under sea water corrosion: A strong corrosion and mechanical damage coupling [J]. International Journal of Fatigue, 2015, 74: 156-165.
R, PALIN-LUC T, BATHIAS C, PARIS P C. Very high cycle fatigue of a high strength steel under sea water corrosion: A strong corrosion and mechanical damage coupling [J]. International Journal of Fatigue, 2015, 74: 156-165.
[5] HE X, WEI Y, HOU L, YAN Z, GUO C, HAN P. Corrosion fatigue behavior of epoxy-coated Mg-3Al-1Zn alloy in gear oil [J]. Transactions of Nonferrous Metals Society of China, 2014, 24: 3429-3440.
[6] TANAKA H, MINODA T. Mechanical properties of 7475 aluminum alloy sheets with fine subgrain structure by warm rolling [J]. Transactions of Nonferrous Metals Society of China, 2014, 24: 2187-2195.
[7] GE R, ZHANG Y, LI Z, WANG F, ZHU B, XIONG B. Fatigue crack growth rate and microstructures of 2E12 and 2524 alloy [J]. Chinese Journal of Rare Metals. 2011, 35(4): 600-606. (in Chinese)
[8] REDA Y, ABDEL-KARIM R, ELMAHALLAWI I. Improvements in mechanical and stress corrosion cracking properties in Al-alloy 7075 via retrogression and reaging [J]. Materials Science and Engineering: A, 2008, 485: 468-475.
[9] LIU Y, WANG Z, KE W. Corrosion behavior of 2024-T3 aluminum alloy in simulated marine atmospheric environment [J]. The Chinese Journal of Nonferrous Metals, 2013, 23: 1208-1216. (in Chinese)
[10] XIANG Y, LIU Y. EIFS-based crack growth fatigue life prediction of pitting-corroded test specimens [J]. Engineering Fracture Mechanics, 2010, 77: 1314-1324.
[11] ERNST P, NEWMAN R C. Pit growth studies in stainless steel foils. I. Introduction and pit growth kinetics [J]. Corrosion Science, 2002, 44: 927-941.
[12] LIU X, ZHANG L, WANG L, WU S, FANG H. Fatigue behavior and life prediction of A7N01 aluminium alloy welded joint [J]. Transactions of Nonferrous Metals Society of China, 2012, 22: 2930-2936.
[13] MOLENT L. Fatigue crack growth from flaws in combat aircraft [J]. International Journal of Fatigue, 2010, 32: 639-649.
[14] van der WALDE K, HILLBERRY B M. Characterization of pitting damage and prediction of remaining fatigue life [J]. International Journal of Fatigue, 2008, 30: 106-118.
[15] DUQUESNAY D L, UNDERHILL P R, BRITT H J. Fatigue crack growth from corrosion damage in 7075-T6511 aluminium alloy under aircraft loading [J]. International Journal of Fatigue, 2003, 25: 371-377.
[16] LARROSA N O, NAVARRO A, CHAVES V. Calculating fatigue limits of notched components of arbitrary size and shape with cracks growing in mode I [J]. International Journal of Fatigue, 2015, 74: 142-155.
[17] MURER N, BUCHHEIT R G. Stochastic modeling of pitting corrosion in aluminum alloys [J]. Corrosion Science, 2013, 69: 139-148.
[18] SUN G, NIU J, WANG D, CHEN S, CAO F. Fatigue life prediction of FSW joints for 2219-T6 aluminum alloy [J]. The Chinese Journal of Nonferrous Metals, 2014, 24: 2460-2464. (in Chinese)
[19] ZHANG Chuan, CHEN Yan-hui, YAO Wei-xing. The use of fractal dimensions in the prediction of residual fatigue life of pre-corroded aluminum alloy specimens [J]. International Journal of Fatigue, 2014, 59: 282-291.
[20] GHIDINI T, DALLE DONNE C. Fatigue life predictions using fracture mechanics methods [J]. Engineering Fracture Mechanics, 2009, 76: 134-148.
[21] ZERBST U, MADIA M, BEIER H T. A model for fracture mechanics based prediction of the fatigue strength: Further validation and limitations [J]. Engineering Fracture Mechanics, 2014, 130: 65-74.
[22] CHAPETTI M D, JAUREGUIZAHAR L F. Fatigue behavior prediction of welded joints by using an integrated fracture mechanics approach [J]. International Journal of Fatigue, 2012, 43: 43-53.
[23] FORMAN R G, SHIVAKUMAR V, NEWMAN J C. Development of the NASA/FLAGRO computer program for analysis of airframe structures [C]//Advanced Structural Integrity Methods for Airframe Durability and Damage Tolerance, Part 2. United States: Langley Research Center, 1994: 277-288.
[24] METTU S R, KONING A D, LOF C J, SCHRA L, MCMAHON J J, FORMAN R G. Stress intensity factor solutions for fasteners in NASGRO 3.0 [J]. ASTM Special Technical Publication, 2000: 2: 133-139.
[25] SKORUPA M, MACHNIEWICZ T, SCHIJVE J, SKORUPA A. Application of the strip-yield model from the NASGRO software to predict fatigue crack growth in aluminium alloys under constant and variable amplitude loading [J]. Engineering Fracture Mechanics, 2007, 74: 291-313.
[26] MORENO B, MARTIN A, LOPEZ-CRESPO P, ZAPATERO J, DOMINGUEZ J. On the Use of NASGRO software to estimate fatigue crack growth under variable amplitude loading in aluminium alloy 2024-T351 [J]. Procedia Engineering, 2015, 101: 302-311.
[27] MAIERHOFER J, PIPPAN R, 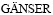 H P. Modified NASGRO equation for physically short cracks [J]. International Journal of Fatigue, 2014, 59: 200-207.
H P. Modified NASGRO equation for physically short cracks [J]. International Journal of Fatigue, 2014, 59: 200-207.
[28] GHAHARI M, KROUSE D, LAYCOCK N, RAYMENT T, PADOVANI C, STAMPANONI M, MARONE F, MOKSO R, DAVENPORT A J. Synchrotron X-ray radiography studies of pitting corrosion of stainless steel: Extraction of pit propagation parameters [J]. Corrosion Science, 2015, 100: 23-35.
[29] ZERBST U, HEINIMANN M, DONNE C D, STEGLICH D. Fracture and damage mechanics modelling of thin-walled structures – An overview [J]. Engineering Fracture Mechanics, 2009, 76: 5-43.
[30] SCHIJVE J. Fatigue of structures and materials in the 20th century and the state of the art [J]. International Journal of Fatigue, 2003, 25: 679-702.
[31] SANGID M D. The physics of fatigue crack initiation [J]. International Journal of Fatigue, 2013, 57: 58-72.
[32] BRAY G H, BUCCI R J, COLVIN E L, KULAK M. Effect of prior corrosion on the S/N fatigue performance of aluminum sheet alloys 2024-T3 and 2524-T3 [C]//Proceedings of the 1996 Symposium on Effects of the Environment on the Initiation of Crack Growth. Orlando, FL, USA: ASTM. 1997: 89-103.
[33] ROKHLIN S I, KIM J Y, NAGY H, ZOOFAN B. Effect of pitting corrosion on fatigue crack initiation and fatigue life [J]. Engineering Fracture Mechanics, 1999, 62: 425-444.
[34] DOLLEY E J, LEE B, WEI R P. Effect of pitting corrosion on fatigue life [J]. Fatigue and Fracture of Engineering Materials and Structures, 2000, 23: 555-560.
[35] Standard Test Method for Exfoliation Corrosion Susceptibility in 2XXX and 7XXX Series Aluminum Alloys (EXCO Test) [S]. 2007.
[36] PARIS P C, GOMEZ M P, ANDERSON W P. A rational analytic theory of fatigue [J]. Trends Engineer, 1961, 13: 9-14.
许 良,于 翔,回 丽,周 松
沈阳航空航天大学 航空制造工艺数字化国防重点学科实验室,沈阳 110136
摘 要:针对航空铝合金(Al-Cu-Mg),提出了一种量化预腐蚀损伤的新方法,该方法将腐蚀坑当量成半椭圆表面裂纹。通过预腐蚀试验、裂纹扩展试验和S-N疲劳试验构建了用于描述疲劳裂纹扩展(FCP)完整阶段的分析模型,并讨论了模型参数与这些疲劳试验数据的关系。基于MATLAB/GUI软件,采用数值积分方法,将当量裂纹尺寸和FCP模型用于计算疲劳寿命。结果表明:FCP模型拟合的S形曲线可以表示裂纹扩展第一阶段至第三阶段的整体变化。此外,预测曲线显示出疲劳寿命的实际变化趋势,并从中获得了疲劳极限的保守结果。因此,对于预腐蚀Al-Cu-Mg合金,尤其是光滑试样,这种新的分析方法可以估算材料的剩余寿命。
关键词:预腐蚀铝合金;腐蚀坑;裂纹扩展;寿命预测;疲劳极限
(Edited by Xiang-qun LI)
Foundation item: Project (SHSYS2015002) supported by the Key Laboratory of Fundamental Science for National Defence of Aeronautical Digital Manufacturing Process, China
Corresponding author: Li HUI; Tel: +86-17792615835; E-mail: syhkyx@163.com
DOI: 10.1016/S1003-6326(17)60156-0

