Al-5.46wt.%Zn-1.67wt.%Mg合金的GP区、亚稳η′相和平衡η相的析出动力学
来源期刊:中国有色金属学报(英文版)2019年第2期
论文作者:A. KHALFALLAH A. A. RAHO S. AMZERT A. DJEMLI
文章页码:233 - 241
关键词:Al-Zn-Mg合金;析出动力学;DSC;JMAK模型;激活能;Avrami常数
Key words:Al-Zn-Mg alloys; precipitation kinetics; DSC; JMAK model; activation energy; Avrami parameter
摘 要:热分析是研究铝合金行为最常用的技术之一,用于分析Guinier-Preston(GP)带的析出及不同相的形成。本文研究Al-5.46wt.%Zn-1.67wt.%Mg合金的行为。用DSC研究GP区、亚稳η′相和平衡η相从室温到480 °C的析出机制与动力学,升温速率为5、10、15和20 °C/min。根据DSC结果,用JMAK模型和等温计算法得到GP、η′和η的表面激活能分别为56、79和96 kJ/mol,而用Kissinger方法和非等温计算法得到三者的表面激活能分别为57、82和99 kJ/mol。GP、η′和η析出过程中,等温计算的Avrami参数(n)值分别为1.103、1.9075和1.92,而非等温计算的n值分别为0.86、2.30和2.24。结果表明,GP区的形成由锌和镁原子的迁移控制,而η′亚稳相和η稳定相的析出由溶质原子的迁移和扩散控制。
Abstract: Thermal analysis is one of the most used techniques for analyzing the behavior of aluminum alloys in order to analyze the precipitation of Guinier-Preston (GP) zones and different phases formed. In the present work, the behavior of the Al-5.46wt.%Zn- 1.67wt.%Mg alloy was studied. The mechanism and kinetics of precipitation of the GP, the metastable phase η′ and the equilibrium phase η were investigated using DSC carried out between room temperature and 480 °C at heating rates of 5, 10, 15 and 20 °C/min. The apparent activation energies, calculated by DSC from isothermal calculation method using JMAK model, for GP, η′ and η were 56, 79 and 96 kJ/mol, respectively, and those calculated by non-isothermal calculation method using Kissinger methods were 57, 82 and 99 kJ/mol, respectively. The values of Avrami parameter, n, from isothermal calculation, during the precipitation of the GP, η′ and η were 1.103, 1.9075 and 1.92, respectively, and those calculated by non-isothermal were 0.86, 2.30 and 2.24, respectively. The results show that GP zones formation is governed by the migration of Zn and Mg atoms while the precipitation of the η′ metastable phase and the η stable phase is governed by both the migration and the diffusion of the solute atoms.
Trans. Nonferrous Met. Soc. China 29(2019) 233-241
A. KHALFALLAH1,2, A. A. RAHO1, S. AMZERT2, A. DJEMLI3
1. University of Sciences and Technology Houari Boumediene, Bab ezzouar Algiers 16111, Algeria;
2. Nuclear Research Centre of Birine, BP 180, Ain Oussera, Djelfa, 17200, Algeria;
3. Department of Physics, University of M’sila, M’sila 28000, Algeria
Received 6 March 2018; accepted 7 November 2018
Abstract: Thermal analysis is one of the most used techniques for analyzing the behavior of aluminum alloys in order to analyze the precipitation of Guinier-Preston (GP) zones and different phases formed. In the present work, the behavior of the Al-5.46wt.%Zn- 1.67wt.%Mg alloy was studied. The mechanism and kinetics of precipitation of the GP, the metastable phase η′ and the equilibrium phase η were investigated using DSC carried out between room temperature and 480 °C at heating rates of 5, 10, 15 and 20 °C/min. The apparent activation energies, calculated by DSC from isothermal calculation method using JMAK model, for GP, η′ and η were 56, 79 and 96 kJ/mol, respectively, and those calculated by non-isothermal calculation method using Kissinger methods were 57, 82 and 99 kJ/mol, respectively. The values of Avrami parameter, n, from isothermal calculation, during the precipitation of the GP, η′ and η were 1.103, 1.9075 and 1.92, respectively, and those calculated by non-isothermal were 0.86, 2.30 and 2.24, respectively. The results show that GP zones formation is governed by the migration of Zn and Mg atoms while the precipitation of the η′ metastable phase and the η stable phase is governed by both the migration and the diffusion of the solute atoms.
Key words: Al-Zn-Mg alloys; precipitation kinetics; DSC; JMAK model; activation energy; Avrami parameter
1 Introduction
Aluminum alloys of 7xxx series AlZnMg are extensively used in the automotive and aerospace industry because of their low density and high mechanical properties. These age-hardenable alloys provide a high strength in the peak-aged conditions [1-5]. The aging behavior and the precipitation sequence may be studied by different methods such as hardness, resistivity measurement, calorimetry and X-ray diffraction technique.
Physical properties of these alloys are linked with the precipitation of metastable precipitates during aging treatments. The decomposition of supersaturated solid solutions obtained by quenching takes place in several stages. The formation of the metastable precipitates leads to a variation of the alloy microstructure [6-9]. The addition of zinc to the Al-Mg alloy system reduces the solid solubility of aluminum in magnesium, increasing the amount of precipitate phase formed upon aging and thus causing a moderate increase in strength [10].
In such a case, it is interesting to study the microstructural evolution of the alloys to correlate the physical properties with the alloy microstructure. Generally, the kinetics of precipitation and dissolution reactions in aluminum alloys was obtained using resistivity and differential scanning calorimetry (DSC) techniques to study the kinetics under isothermal conditions and under non-isothermal conditions, respectively. The decomposition of the supersaturated solid solution is known to take place via the formation of several phases which may precipitate simultaneously. Depending on thermal treatment, the unmixing processes can be described as follows [11-14]: α-supersaturated solid solution (α-sss) → GP zones (Zn,Mg) → metastable η′ (Hex.) → stable η (MgZn2) (Hex.).
In the age-hardenable aluminium alloys, the precipitation is the subject of many experimental and theoretical works [11,15-17]. In the AlZnMg alloys, the hardening is attributed to the precipitation of the GP zones and the η′ metastable phase which, generally but not necessarily, nucleates from the GP zones [18]. The precipitation and the dissolution of all the phases of the precipitation sequence are accompanied by exothermic and endothermic reactions which may be investigated by the differential scanning calorimetry (DSC) technique [19-21].
In the present work, the transformation kinetics of precipitation of the GP zone and metastable phase η′ and equilibrium phase η has been investigated by DSC in order to estimate the activation energies of GP, η′ and η formations based on isothermal and non-isothermal methods, the growth morphology parameter n and the frequency factor for the reaction of GP, η′ and η formations.
2 Experimental
2.1 Materials and samples preparation
The Al-5.46wt.%Zn-1.67wt.%Mg alloy studied was prepared from an aluminium powder of 99.98% purity. Its chemical composition is given in Table 1.
Table 1 Chemical composition of Al-5.46wt.%Zn- 1.67wt.%Mg alloy (mass fraction, %)

The microstructural structure of Al-Zn-Mg alloy was observed using a metallographic microscope Leica DM2500 M equipped with a photographic camera. X-ray diffraction patterns were registered using a Philips X-Pert PW1500 with a monochromatic Cu Kα radiation of a wavelength of 0.15405 nm. The thermal analysis (DSC) was carried out on a Setaram LABSYS Evo TG-DSC 1600 °C equipment, operated under argon atmosphere.
2.2 Theoretical concept
The determination of the kinetics parameters describing the precipitation kinetics of the GP zones, the η′ metastable phase and the η stable phase is based on an isothermal calculation method and on a non-isothermal calculation method.
2.2.1 Isothermal calculation method
The isothermal calculation method is based on the JOHNSON-MEHL-AVRAMI-KOLMOGOROV (JMAK) theory. The evolution of the transformed fraction during a phase precipitation is given by
x=1-exp[(-kt)n] (1)
where x is the transformed fraction at time t, k is the rate constant which has an Arrhenian temperature dependence:
k=k0exp[-Ea/(RT)] (2)
where k0 is the frequency factor, Ea is the activation energy, and R the gas constant.
The transformed fraction is determined from the DSC thermograms for different heating rates using the relation:
x=AT/A (3)
where AT represents the area under the peak at the temperature T and A is the total area of the peak.
The rate of transformation dx/dt is expressed by
 (4)
(4)
where F(x) is a function of the transformed fraction [22].
So, Eqs. (5) and (6) exist:
 (5)
(5)
 (6)
(6)
From the DSC analysis at different heating rates, the activation energy, the frequency factor and the Avrami parameter can be determined.
For each transformed fraction x at different heating rates, the apparent activation energy is determined from the slope of the curve ln(dx/dt) versus 1/T and the values of ln[k0F(x)] are given by
 (7)
(7)
The Avrami parameter n, is determined by choosing some pairs of x1 and x2 that satisfy the following condition:
ln[k0F(x1)]= ln[k0F(x2)] (8)
So, n will be given by
 (9)
(9)
The frequency factor k0 could be deduced from Eq. (6) after the determination of n.
2.2.2 Non-isothermal concept
Several methods in the non-isothermal DSC experiment may be used to calculate the apparent activation energy in the non-isothermal DSC experiment. In this work, the single Kissinger [23-26] method was chosen:
 (10)
(10)
where v is the heating rates in the DSC analysis; TP is the absolute peak temperature on DSC curves; C is a constant. The activation energy is deduced from the
slope of the curve  .
.
The values of the Avrami parameters are deduced for each heating rate from the following equation [26-28]:
 (11)
(11)
where △TP is the width of the transformation peak at half maximum.
3 Results and discussion
3.1 Optical microscopy
The optical microscopy technique was applied for the analysis of the microstructure of the alloy. The optical micrograph of the homogeneous alloy shows a granular structure including some intermetallic insoluble particles containing Si and Fe (Fig. 1(a)) and that of the homogeneous alloy heated to 290 °C at a rate of 10 °C/min shows stable particles MgZn2 in the grains and at the grain boundaries (Fig. 1(b)).

Fig. 1 Optical micrographs of as-cast Al-Zn-Mg alloy
3.2 X-ray diffraction characterization
X-ray diffraction patterns show that the diffraction peaks of the as-quenched solid solution are at analogous positions of those of the aluminum and, after a heating from room temperature to 290 °C, the diffraction patterns show the diffraction peaks of the η (MgZn2) stable precipitate (Fig. 2).
3.3 DSC analysis
During the heating from room temperature to 480 °C, using heating rates of 5, 10, 15 and 20 °C/min, the DSC thermograms (Fig. 3) show exothermic and endothermic peaks corresponding to the precipitation and the dissolution of the GP zones, the η′ (MgZn2) metastable phase and the η (MgZn2) stable phase in accordance with the precipitation sequence.

Fig. 2 XRD patterns of pure aluminum (a), Al-Zn-Mg as-quenched solid solution (b), and Al-Zn-Mg solid solution after heating from room temperature to 290 °C (c)
The different peaks are noted by A for the GP zones precipitation, B for the precipitation of the η′ metastable phase and C for the precipitation of the η stable phase (Table 2).
The shifting of the peak temperatures to the higher temperatures with the increase of the heating rate is due to the fact that the precipitation reaction is thermally activated [29-33].
3.3.1 Isothermal calculation of precipitation kinetics
During the precipitation of a phase, the transformed fraction, x, is determined from the DSC thermograms for different heating rates using Eq. (2). Figure 4 shows the transformed fraction and rate of transformed fraction during the precipitation of the GP zones, the η′ metastable phase and the η stable phase.

Fig. 3 DSC diagram of Al-Zn-Mg alloy heated at 10 °C/min
Table 2 Temperature of peaks for GP zones (A), η′ metastable phase (B) and η stable phase (C)

The shape of the transformed volume fraction curves suggests that the precipitation kinetics obeys to the JMAK law of the growth controlled by the solute atom diffusion [34-36].
Figure 5 represents the variations of dx/dt versus time during the precipitation of the GP zones, the η′ metastable phase and the η stable phase. The rate of transformation increases with the increase in the heating rate.
Figure 6 shows the plots of ln(dx/dt) and 1/T versus transformed fraction x during the precipitation of the GP zones, the η′ metastable phase and the η stable phase at different heating rates from DSC experiment.
The values of the apparent activation energy for different transformed fractions, determined from the slopes of the linear curves ln(dx/dt) versus 1/T plotted for different transformed fractions at different heating rates (Fig. 7) are listed in Table 3. The correlation factor, R2, greater than 0.99, indicates that there is a strong linear relationship between ln(dx/dt) and 1/T.
Figure 8 shows the plots of ln[k0F(x)] versus transformed fraction x during the GP zone precipitation, the metastable phase precipitation and the stable phase precipitation at different heating rates. We could deduce the Avrami parameter by choosing some pairs of x1 and x2 that satisfy the following condition: ln[k0F(x1)]= ln[k0F(x2)]. The average values of Avrami parameter n, for each heating rate are listed in Table 4 using Eq. (9). The frequency factor k0 is determined from Eq. (6).
3.3.2 Non-isothermal calculation of precipitation kinetics
In the case of the non-isothermal calculation method, the activation energy is determined by the Kissinger relation. The apparent activation energies, determined by the Kissinger method from the slope of the linear curves  versus 1/TP (Fig. 9) are listed in Table 5, which are in the order of 57 kJ/mol during the GP zones precipitation, in the order of 82 kJ/mol during the precipitation of the η′ metastable phase and in the order of 99 kJ/mol during the precipitation of the η stable phase. The correlation factor, R2, greater than 0.99, indicates that there is a strong linear relationship between
versus 1/TP (Fig. 9) are listed in Table 5, which are in the order of 57 kJ/mol during the GP zones precipitation, in the order of 82 kJ/mol during the precipitation of the η′ metastable phase and in the order of 99 kJ/mol during the precipitation of the η stable phase. The correlation factor, R2, greater than 0.99, indicates that there is a strong linear relationship between  and 1/TP.
and 1/TP.
The obtained results are in accordance with those of OHTA et al and AFIFY et al [37-39].
The Avrami parameter n is determined from Eq. (11) and, the values and average values of n are listed in Table 6. The average values of n, during the GP zones formation, are characteristics of a growth of plate after saturation of nucleation, while the average values of n, during the precipitation of the η′ metastable phase and during the precipitation of the η stable phase are characteristics of a continuous nucleation and diffusion controlled growth [40].

Fig. 4 Transformed fractions and rates of transformed fraction at different heating rates during GP zone precipitation (a), η′ metastable phase precipitation (b) and η stable phase precipitation (c)

Fig. 5 Growth rate dx/dt of GP zones (a), η′ metastable phase (b) and η stable phase (c) versus time at different heating rates

Fig. 6 Plot of ln(dx/dt) and 1/T versus transformed fraction x during precipitation of GP zones (a), η′ metastable phase (b) and η stable phase (c) at different heating rates

Fig. 7 Plots of ln(dx/dt) versus 1/T for each transformed fraction x during precipitation of GP zones (a), η′ metastable phase (b) and η stable phase (c) at different heating rates
Table 3 Activation energy (Ea) and coefficient of determination (R2) for different transformed fraction x

Table 4 Values of Avrami parameter and frequency factor at different heating rates


Fig. 8 Plots of ln[k0F(x)] versus transformed fraction x during precipitation of GP zones (a), η' metastable phase (b) and η stable phase (c) at different heating rates
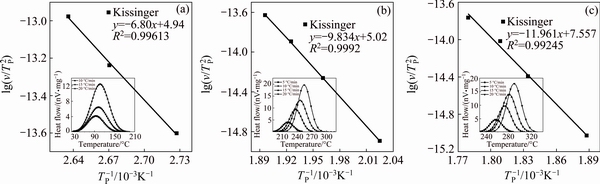
Fig. 9 Plots of  versus 1/TP at different heating rates during precipitation of GP zones (a), η' metastable phase (b) and η stable phase (c)
versus 1/TP at different heating rates during precipitation of GP zones (a), η' metastable phase (b) and η stable phase (c)
Table 5 Values of Ea and R2 for GP zone, η′ metastable phase and η stable phase by using Kissinger method from DSC experiment

Table 6 Values of n for GP zones, η′ metastable phase and η stable phase at different heating rates

It is well known that the activation energy results from the contribution of the vacancies formation and the vacancies migration. During the GP zones formation, the determined apparent activation energy, in the order of 57 kJ/mol, is close to the activation energies of the migration of the Zn and Mg solute atoms in the aluminum, which are determined to be in the order of 53 and 60 kJ/mol [41], respectively. In such a case, during the GP zones formation, the determined apparent activation energy of 57 kJ/mol is characteristic of the migration of Zn and Mg atoms. The determined apparent activation energies during the precipitation of the η′ metastable phase and the η stable phase, in the order of 82 and 99 kJ/mol, respectively, are much greater than the activation energies of the migration of Zn and Mg atoms in aluminum and lower than the activation energies of their diffusion in aluminum, including the migration and formation energies of the vacancies, estimated to be in the order of 130 and 120 kJ/mol, respectively [41,42]. So, the precipitations of the η′ metastable phase and the η stable phase result from both the migration and the diffusion of the solute atoms. This is due to the high supersaturation of the atoms in vacancies and to their elimination at the different sinks during the heating.
4 Conclusions
(1) The DSC experiments highlight the precipitation sequence in the AlZnMg alloy. The shift of the peak temperature to the higher temperature with the increase of the heating rate confirms that the precipitation and the dissolution reactions are thermally activated.
(2) All JMAK parameters n, k0 and the apparent activation energy Ea, were determined using both an isothermal calculation and a non-isothermal calculation during the precipitation of the GP zones, the η′ metastable phase and the η stable phase.
(3) The results also show that GP zones formation is governed by the migration of Zn and Mg atoms while the precipitation of the η′ metastable phase and the η stable phase is governed both by the migration and the diffusion of the solute atoms.
Acknowledgments
One of the authors, A. KHALFALLAH, would like to thank the Director General of the CRNB for funding the research project, as well as Mr. Fahd ARBAOUI, head of the Reactor Chemistry Department, for allowing to work in his laboratories without forgetting Mr. Pr. Fodile SAHNOUN at University of M’sila for having authorized to use the DSC equipment as well as Noureddine Salemi Researcher at the CRNB, who carried out the XRD analyses.
References
[1] SEPEHRBAND P, ESMAEILI S. Application of recently developed approaches to microstructural characterization and yield strength modeling of aluminum alloy AA7030 [J]. Materials Science and Engineering A, 2008, 487: 309-315.
[2] WU H, WEN S P, LU J T, MI Z P, ZENG X L, HUANG H, NIE Z R. Microstructural evolution of new type Al-Zn-Mg-Cu alloy with Er and Zr additions during homogenization [J]. Transactions of Nonferrous Metals Society of China, 2017, 27: 1476-1482.
[3] STARINK M J, LI X M. A model for the electrical conductivity of peak-aged and overaged Al-Zn-Mg-Cu alloys [J]. Metallurgical and Materials Transactions A, 2003, 34: 899-911.
[4] SUAREZ M A, ALVAREZ O, ALVAREZ M A, RODRIGUEZ R A, VALDEZ S, JUAREZ J A. Characterization of microstructures obtained in wedge shaped Al-Zn-Mg ingots [J]. Journal of Alloys and Compounds, 2010, 492: 373-377.
[5] WANG F, ZHANG J, XIONG B, ZHANG Y. Effect of Fe and Mn additions on microstructure and mechanical properties of spray- deposited Al-20Si-3Cu-1Mg alloy [J]. Materials Characterization, 2009, 60: 384-388.
[6] DANH N C, RAJAN K, WALLACE W. A TEM study of microstructural changes during retrogression and reaging in 7075 aluminium [J]. Metallurgical and Materials Transactions A, 1983, 14: 1843-1850.
[7] RAJAN K, WALLACE W, BEDDOES J C. Microstructural study of a high strength stress corrosion resistant 7075 aluminium alloy [J]. Journal of Materials Science, 1982, 17: 2817-2824.
[8] STILLER K, WARREN P J, HANSEN V, ANGENETE J, GJONNES J. Investigation of precipitation in an AlZnMg Alloy after two step aging treatment at 100 and 150 °C [J]. Materials Science and Engineering A, 1999, 270: 55-63.
[9] MONDOLFO L F. Structure of the aluminium: Magnesium: zinc alloys [J]. Metallurgical Reviews, 1971, 153: 95-124.
[10] CELOTTO S. TEM study of continuous precipitation in Mg-9wt%Al-1wt%Zn alloy [J]. Acta Materialia, 2000, 48: 1775-1787.
[11] DESCHAMPS A, LIVET F, BRECHET Y. Influence of predeformation on ageing in an Al-Zn-Mg alloy—I. Microstructure evolution and mechanical properties [J]. Acta Materialia, 1998, 47: 281-292.
[12] DEGISCHER H P, LACOM W, ZAHRA A, ZAHRA C Y. Decomposition processes in an Al-5%Zn-1%Mg alloy: II. Electromicroscopic Investigation [J]. Zeitschrift Fur Metallkunde, 1980, 71: 231-238.
[13] BERG L K,  J, HANSEN V, LI X Z, KNUTSON-WEDEL M, WATERLOO G, SCHRYVERS D, WALLENBERG L R. GP-zones in Al-Zn-Mg alloys and their role in artificial aging [J]. Acta Materialia, 2001, 49: 3443-3451.
J, HANSEN V, LI X Z, KNUTSON-WEDEL M, WATERLOO G, SCHRYVERS D, WALLENBERG L R. GP-zones in Al-Zn-Mg alloys and their role in artificial aging [J]. Acta Materialia, 2001, 49: 3443-3451.
[14] LI X Z, HANSEN V,  J, WALLENBERG L R. HREM study and structure modeling of the η′ phase, the hardening precipitates in commercial Al-Zn-Mg alloys [J]. Acta Materialia, 1999, 47: 2651-2659.
J, WALLENBERG L R. HREM study and structure modeling of the η′ phase, the hardening precipitates in commercial Al-Zn-Mg alloys [J]. Acta Materialia, 1999, 47: 2651-2659.
[15] EMBURY J D, DESCHAMPS A, BRECHET Y. The interaction of plasticity and diffusion controlled precipitation reactions [J]. Scripta Materialia, 2003, 49: 927-932.
[16] GUYOT P, COTTIGNIES L. Precipitation kinetics, mechanical strength and electrical conductivity of AlZnMgCu alloys [J]. Acta Materialia, 1996, 44: 4161-4167.
[17] LENDVAI J. Precipitation and strengthening in aluminium alloys [J]. Materials Science Forum, 1996, 217: 43-56.
[18] MALONEY S K, HONO K, POLMEAR I J, RINGER S P. The effects of a trace addition of silver upon elevated temperature ageing of an Al-Zn-Mg alloy [J]. Micron, 2001, 32: 741-747.
[19] HUANG Z, HARRIS A, MALOY S A, HOSEMANN P. Nanoindentation creep study on an ion beam irradiated oxide dispersion strengthened alloy [J]. Journal of Nuclear Materials, 2014, 451: 162-167.
[20] GHOSH K S, GAO N. Determination of kinetic parameters from calorimetric study of solid state reactions in 7150 Al-Zn-Mg alloy [J]. Transactions of Nonferrous Metals Society of China, 2011, 21: 1199-1209.
[21] KREUZEDER M, ABAD M D, PRIMORAC M M, HOSEMANN P, MAIER V, KIENER D. Fabrication and thermo-mechanical behavior of ultra-fine porous copper [J]. Journal of Materials Science, 2015, 50: 634-643.
[22] SURINACH S, BARO M D, CLAVAGUERA-MORA M T, CLAVAGUERA N. Kinetic study of isothermal and continuous heating crystallization in GeSe2-GeTe-Sb2Te3 alloy glasses [J]. Journal of Non-crystalline Solids, 1983, 58: 209-217.
[23] KISSINGER H E. Reaction kinetics in differential thermal analysis [J]. Analytical Chemistry, 1957, 29: 1702-1706.
[24] ZHAN G, YU J X, XU Z G, ZHOU F, CHI R A. Kinetics of thermal decomposition of lanthanum oxalate hydrate [J]. Transactions of Nonferrous Metals Society of China, 2012, 22: 925-934.
[25] COATS A W, REDFERN J P. Kinetic parameters from thermogravimetric data [J]. Nature, 1964, 201: 68-69.
[26] REDAOUI D, SAHNOUNE F, HERAIZ M, BELHOUCHET H, FATMI M. Thermal decomposition kinetics of Algerian Tamazarte kaolinite by thermogravimetric analysis [J]. Transactions of Nonferrous Metals Society of China, 2017, 27: 1849-1855.
[27] RAY C S, HUANG W, DAY D E. Crystallization kinetics of a lithia–silica glass: Effect of sample characteristics and thermal analysis measurement techniques [J]. Journal of the American Ceramic Society, 1991, 74: 60-66.
[28] AUGIS J, BENNETT J. Calculation of the Avrami parameters for heterogeneous solid state reactions using a modification of the Kissinger method [J]. Journal of Thermal Analysis and Calorimetry, 1978, 13: 283-292.
[29] GHOSH K S, DAS K, CHATTERJEE U K. Kinetics of solid-state reactions in Al-Li-Cu-Mg-Zr alloys from calorimetric studies [J]. Metallurgical and Materials Transactions A, 2007, 38: 1965-1975.
[30] JENA A K, GUPTA A K, CHATURVEDI M C. A differential scanning calorimetric investigation of precipitation kinetics in the Al-1.53wt%Cu-0.79wt%Mg alloy [J]. Acta Metallurgica, 1989, 37: 885-895.
[31] GUPTA A K, JENA A K, CHATURVEDI M C. A differential technique for the determination of the activation energy of precipitation reactions from differential scanning calorimetric data [J]. Scripta Metallurgica, 1988, 22: 369-371.
[32] COLLEY L J, WELLS M A, POOLE W J. Microstructure–strength models for heat treatment of Al-Si-Mg casting alloys: I: Microstructure evolution and precipitation kinetics [J]. Canadian Metallurgical Quarterly, 2014, 53: 125-137.
[33] GHOSH K S, DAS K, CHATTERJEE U K. Calorimetric studies of 8090 and 1441 Al-Li-Cu-Mg-Zr alloys of conventional and retrogressed and reaged tempers [J]. Journal of Materials Science, 2007, 42: 4276-4290.
[34] LUO A, LLOYD D J, GUPTA A, YOUDELIS W V. Precipitation and dissolution kinetics in Al-Li-Cu-Mg alloy 8090 [J]. Acta Metallurgica et Materialia, 1993, 41: 769-776.
[35] VYAZOVKIN S, WIGHT C A. Isothermal and non-isothermal kinetics of thermally stimulated reactions of solids [J]. International Reviews in Physical Chemistry, 1998, 17: 407-433.
[36] BROWN M E. Handbook of thermal analysis and calorimetry [M]. Amsterdam: Elsevier, 1998.
[37] MATUSITA K, SAKKA S. Kinetic study of crystallization of glass by differential thermal analysis—Criterion on application of Kissinger plot [J]. Journal of Non-Crystalline Solids, 1980, 38: 741-746.
[38] OHTA M, KOBAYASHI T, SAKAKIBARA A. On the apparent activation energy for clustering in dilute Al-Zn alloys [D]. Memoirs of the School of Engineering, Okayama University, 1978: 77-88.
[39] GAO N, STARINK M J, LANGDON T G. Using differential scanning calorimetry as an analytical tool for ultrafine grained metals processed by severe plastic deformation [J]. Materials Science and Technology, 2009, 25: 687-698.
[40] STARINK M. Analysis of aluminum based alloys by calorimetry: Quantitative analysis of reactions and reaction kinetics [J]. International Materials Reviews, 2004, 49: 191-226.
[41] YANNACOPOULOS S, KASAP S O, HEDAYAT A, VERMA A. An experimental study of phase transformations in an Al-Zn-Mg-Zr alloy: DSC and hot microhardness measurements [J]. Canadian Metallurgical Quarterly, 1994, 33: 51-60.
[42] ASANO K, HIRANO K I. Precipitation process in an Al-Zn-Mg alloy [J]. Transactions of the Japan Institute of Metals, 1968, 9: 24-34.
A. KHALFALLAH1,2, A. A. RAHO1, S. AMZERT2, A. DJEMLI3
1. University of Sciences and Technology Houari Boumediene, Bab ezzouar Algiers 16111, Algeria;
2. Nuclear Research Centre of Birine, BP 180, Ain Oussera, Djelfa, 17200, Algeria;
3. Department of Physics, University of M’sila, M’sila 28000, Algeria
摘 要:热分析是研究铝合金行为最常用的技术之一,用于分析Guinier-Preston(GP)带的析出及不同相的形成。本文研究Al-5.46wt.%Zn-1.67wt.%Mg合金的行为。用DSC研究GP区、亚稳η′相和平衡η相从室温到480 °C的析出机制与动力学,升温速率为5、10、15和20 °C/min。根据DSC结果,用JMAK模型和等温计算法得到GP、η′和η的表面激活能分别为56、79和96 kJ/mol,而用Kissinger方法和非等温计算法得到三者的表面激活能分别为57、82和99 kJ/mol。GP、η′和η析出过程中,等温计算的Avrami参数(n)值分别为1.103、1.9075和1.92,而非等温计算的n值分别为0.86、2.30和2.24。结果表明,GP区的形成由锌和镁原子的迁移控制,而η′亚稳相和η稳定相的析出由溶质原子的迁移和扩散控制。
关键词:Al-Zn-Mg合金;析出动力学;DSC;JMAK模型;激活能;Avrami常数
(Edited by Xiang-qun LI)
Corresponding author: A. KHALFALLAH; E-mail: kada28000@gmail.com
DOI: 10.1016/S1003-6326(19)64932-0

