DOI: 10.11817/j.issn.1672-7207.2016.12.043

树冠流动阻力特性数值模拟与实验研究

杨会^{1, 2}，付海明¹

(1. 东华大学 环境科学与工程学院，上海，200051；

2. 桂林航天工业学院 能源与建筑环境学院，广西 桂林，541004)

摘要：为深入分析树冠内部结构参数对树冠绕流流动阻力的影响，采用数值模拟和实验测试相结合的方法研究几种典型形态特征树冠的内部流场特征和流动阻力。用树冠叶面积指数(L_AI)、稠密度(S_VF)和分形维数(D_f)表征树冠复杂的形态结构，讨论树冠形态结构参数对树冠流动阻力的影响规律。研究结果表明：模型叶面积指数与稠密度呈近似线性关系，而树冠分形维数分别与树冠稠密度和叶面积指数满足近似对数关系。通过对数值模拟计算结果回归分析，给出树冠流动阻力系数与叶面积指数的关系式。研究结果表明：真实条件下的树冠流动阻力结果要明显高于二维简化模型的数值计算结果，但二者在变化趋势上表现出较好的一致性；在引入树冠阻力系数修正系数后，数值计算结果与实验结果吻合较好。

关键词：树冠；流动阻力；树冠阻力系数；叶面积指数

中图分类号：X513; S731.2             文献标志码：A         文章编号：1672-7207(2016)12-4292-09

Numerical simulation and experimental study of canopy flow resistance characteristics

YANG Hui^{1, 2}, FU Haiming¹

(1. School of Environmental Science and Engineering, Donghua University, Shanghai 200051, China;

2. Department of Building Environment and Energy Engineering,

Guilin University of Aerospace Technology, Guilin 541004, China)

Abstract: Computational fluid dynamics (CFD) and field experiments were used to investigate the flow characteristics and flow resistance through vegetation canopies with several typical morphological characteristics. The leaf area index (L_AI), solid volume fraction (S_VF) and the fractal dimension (D_f) were used to analyze the complicated morphology of vegetation canopy. The influences of leaf area index, solid volume fraction and fractal dimension on flow resistance were studied. The results show that leaf area index approximately has linear relationship with solid volume fraction, and the fractal dimension of canopy has logarithmic relationship with leaf area index and solid volume fraction, respectively. A model expression between the drag coefficient of the canopy and leaf area index was presented by analyzing simulation results. The model expression was validated using experimental results in a wind tunnel with four kinds of tree branches. The results show that the simulation results from 2D simplified model are slightly larger than experimental results, and can qualitatively predict the trend of the relationship between the drag coefficient of the canopy and leaf area index. However, the results obtained by using the proposed 2D simplified canopy model show good agreement with the experimental results after modifying the simulation results with a correction factor.

Key words: canopy; flow resistance; drag coefficient of canopy; leaf area index

树具有保持水土、防风固沙、涵养水源、调节气候、减少污染物等功能。树冠系指乔木树干和其他的连同集生枝叶的部分，其状如冠，通常将自然形成的树冠称为自然树冠，而将经过人工修剪造型而成的树冠则称为人工树冠。长期以来，针对风场作用下树冠流场特性研究主要是采用野外观测、风洞试验以及数值模拟。如CAO等^[1]通过边界层风动实验装置测定3种树冠阻力特性、风速分布以及尖端位移; SANZ等^[2]于风洞实验中使用粒子成像测速仪测定二维森林冠层流动及湍流特性；MOLINA-AIZ等^[3] 通过风洞试验测了4种园艺植物的阻力系数C_D；DUMAN等^[4]在大气边界层内实测得了树冠气流的速度损耗和湍流耗散；IRVINE等^[5]则实测了北美典型云杉林的风场和湍流强度特征。NOVAK等^[6]利用Dantec三轴热线探针测定变叶面积密度的人造树的风速及湍动能分布。国内也有少量研究者开展了树冠流场特性的研究，如关德新等^[7]利用多年的林带疏透度、透风系数的野外观测和风洞实验测试结果给出了立体型林带和平面型林带疏透度和透风系数的关系式，在此基础上讨论了林带阻力系数与疏透度和透风系数的关系。目前，由于测试条件的限制，试图通过实验手段完全了解树冠内外流场分布仍十分困难。如野外对真实树冠进行流场测试时，来流风速不受人为控制，且树冠较为高大不易测量；若进行风洞测试，则因风洞较小，难以获得真实环境下近地面来流风场速度分布；此外，实验也难以获得树冠内外流场的精细结构。数值模拟则提供了一种有效的研究方法。ZENG等^[8]利用一阶闭合模型来预测树冠内外空气流速，而SIQUEIRA等^[9]的研究结果表明二阶闭合模型在求解ε输运方程方面更有优势。SOGACHEV等^[10-11]提出并验证考虑树冠阻力的改进两方程(E-φ)模型以及一种通过增加附加方程来减小模拟拟冠层流动和边界层流动不确定的方法。MOCHIDA等^[12]将源于实验结果的模型参数运用k-ε湍流模型，并预测风速分布以及能量损失。HIRAOKA等^[13]在假设弥散量远小于雷诺应力的前提下运用k-ε湍流模型模拟树冠流动，所得数值模拟结果与实验结果吻合良好。李亮等^[14]用带源项k-ε模型模拟了三维树冠流场分布，结果表明数值计算获得的速度、k及ε参量的空间分布与GREEN^[15]的实验值吻合较好。HUANG等^[16-17]运用大涡模型(LES)模拟三维森林边界湍流特性。DUPONT等^[18]运用大涡模型(LES)以及改进的气象模型高级区域预报系统模拟树冠内外湍流特性。PATTON等^[19]利用大涡模型(LES)模拟并分析覆盖有稀疏及浓密斜坡的压力场和速度分布。YANG等^[20-21]也采用大涡模型分析了空气穿越树冠时所产生的回流特征，并讨论了回流区与叶面积指数(L_AI)之间的相互关系；BELCHER等^[22]提出综合分析讨论复杂地势和森林边界对湍流统计量的影响。然而，上述研究主要是针对树冠外部的流场特征，且未涉及树冠阻力系数与树冠形态特征的关系。由于树冠的树叶形式的多样性及树叶数量巨大，直接模拟具有叶片尺度特征的树冠内部流场的精细结构目前尚存诸多计算手段上的困难，不同形状的树冠对流场的影响也有所不同，对树冠所作简化越多，相应的计算结果误差也会偏大。SVENSSON等^[23]将树冠简化为2.5 m高、阻力系数为0.3、叶面积密度为2.1 m^-1的长方形来研究二维树冠内外的流场分布；同样地，IRVINE等^[5]和GASH^[24]也分别把三维树冠简化为二维长方形区域来研究森林边界处流场分布。李亮等^[14]将三维树冠简化为四棱锥、四棱台、圆锥及长方体，比较分析不同简化的树冠模型内外流场分布差异。在前人的基础上，本文作者考虑将三维复杂的树冠结构进行简化，采用圆环表征由众多树叶组成的团簇，建立二维树冠结构简化模型。在树叶团簇尺度上模拟树冠内部流场的精细结构和阻力特性。为获得真实条件下树冠的流动阻力特性，选取4种典型形态结构的树枝进行风洞试验，进一步探索树冠阻力特性与其形态结构的关联性，试图给出树冠流动阻力系数估计的简洁模型。

1  物理模型

考虑图1所示的二维计算平面域，计算流域高为9 m，流域长为39 m。树冠高度为3 m，流域高度设为9 m，即三倍树冠高度，故可忽略流域高度对流场求解结果的影响。为保证入口边界和出口边界处流动的充分发展，设定树冠到流体入口距离为9 m，亦为3倍树高，树冠到流体出口边界距离为30 m，即10倍树高。流域被划分为390×90个非均匀三角形网格，并对树冠内部作局部网格加密处理。边界条件设置如下：地面设置为无滑移粗糙壁面，粗糙度取5 mm，并假设壁面无明显的障碍物和植被；流域上部设置为滑移边界，滑移速度与来流速度相同；流体进出口分别设为速度入口边界和压力出口边界；树冠轮廓和树叶团簇轮廓分别设置为内部边界(interior边界)和粗糙无滑移壁面，粗糙度取0.2 mm。

为简化分析，现对问题进行如下基本假设：1) 流体流动为不可压缩、无旋、定常二维流；2) 大气环境为中性，且忽略Coriolis力，其中Coriolis力是对旋转体系中进行直线运动的质点由于惯性相对于旋转体系产生的直线运动的偏移的一种描述，源于物体运动所具有的惯性。

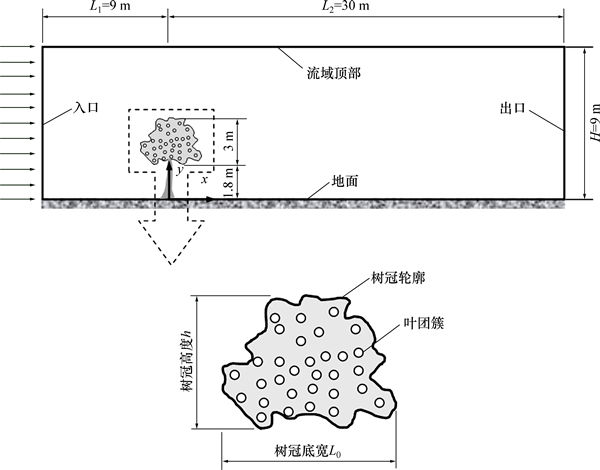
图1  计算区域及边界条件(树叶团簇的当量直径D_I=4.84 cm，L_AI=5.3)

Fig. 1  Calculation domain for wind flow and boundary conditions

在上述假设条件下，树冠绕流流动的动量方程和连续性方程分别为：

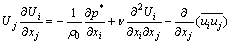    (1)

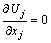               (2)

式中：U_i为i方向上平均速度分量；p*为实际压力与参考值之差；u_i为平均速度U_i的脉动值；ρ₀为空气密度；ν为空气运动学黏度。

雷诺应力项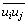可根据网格变数解析定义为

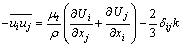      (3)

式中：μ_t为涡黏性；δ_ij为Kronecker δ函数；k为湍流动能。由k和ε定义速度的比例尺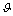和长度比例尺l分别为

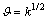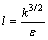，             (4)

在k-ε湍流模型中，涡黏性μ_t定义为

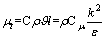             (5)

式中：C_μ为经验常数。

         本文采用LAUNDER等^[25]提出的标准k-ε湍流模型。湍动能及其耗散速率方程分别为：

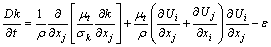 (6)

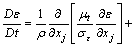
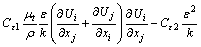     (7)

式中：σ_k，σ_ε，C_ε1和C_ε2为经验常数^[26]，见表1。

表1  标准k-ε湍流模型各经验常数

Table 1  Turbulent constants for standard k-ε turbulent model

2  风洞实验

为了验证简化树冠阻力模型的可行性，选取4种不同的树枝进行风洞实验以验证数值模拟结果。风洞实验装置如图2所示，图中A和B为压差测试点。图3所示为桂花、竹子、广玉兰和八角金盘4种典型实验用树枝结构，这4种树种植面广且形态差异较大，故将它们作为实验树种具有一定代表性。

分别将上述4种树枝置于测试段(圆形风筒)，每种树枝设定5种不同叶面积指数，共计进行20组实验。叶面积指数通过控制实验树枝的数量以及叶片数来实现。叶面积指数取值范围为0~20。根据叶面积指数定义可知，测试段7内树枝所有叶片总面积与测试段7底面积之比即为叶面积指数。实验时，通过无级变频装置2(0~50 Hz内无级调节)和蜂窝栅极6均匀向测试段输送速度1.0~15.4 m/s的连续风速。并在测试段7的A和B两点采用数字压差计测量气流通过树枝前后的压力损失，A和B两点分别在测试段圆周上均匀取6个测试点以测出A和B两点平均静压差。测试段7尾部通向大气，每变换一次风速等待片刻，待风速均匀稳定后再进行测试。风速测量可以通过孔板流量计间接测得，也可以直接在测试段7使用热线风速仪测量。为获得更高的测量精度，本实验采用后者。

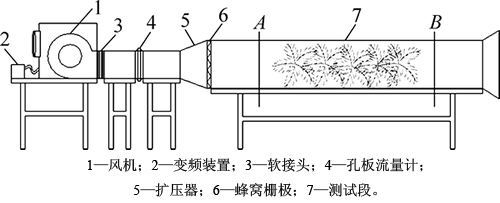
图2  风动实验装置

Fig. 2  Apparatus of wind tunnel for airflow experiment

图3  4种实验树枝

Fig. 3  Four kinds of experimental tree branches

3  结果与讨论

为定量描述树冠的形态结构，先给出描述树冠形态结构的3个基本参量(树冠稠密度S_VF、树冠分形维数D_f、树冠叶面积指数L_AI)的定义及计算方法。在本文所讨论的二维树冠简化模型条件下(见图1)，二维叶面积指数定义为：所有叶团簇周长比二维树冠底宽，即L_AI=n×π×D_I/L₀(其中，D_I为树叶团簇的当量直径，L₀为二维树冠底宽，n为树叶团簇的数量)。稠密度S_VF定义为：所有叶团簇的面积比二维树冠面积，计算式为S_VF=n×π×D_I²/(4S)(其中S为二维树冠面积，即树冠轮廓所围成的面积)。保持树冠轮廓大小和形状不变，通过改变叶团簇的当量直径D_I或树叶团簇的数量，构成不同的树冠模型，依据上述给出的树冠形态描述参量的计算式，分别计算出相应模型的树冠分形维数、叶面积指数及稠密度。本文中的树冠分形维数D_f采用盒维数方法计算^[27]，最后应用计算流体力学软件Fluent对树冠模型进行数值计算，讨论树冠阻力系数与树冠形态结构的关系，并将树冠流场模拟结果与文献结果进行比较，以验证这种树冠简化方法的可行性。最后在数值模拟和实验结果基础上拟合给出树冠阻力系数与这3个基本参量的关系式。

根据上述模型与方法以及大量学者的研究可知：树冠阻力系数C_n与树冠稠密度S_VF、树冠分形维数D_f以及叶面积指数L_AI有关，即C_n=f(S_VF，D_f，L_AI)。如MOLINA-AIZ等^[3]通过风洞实验探究了树冠阻力系数与叶面积密度的关系，GRANT等^[28]进行现场测试探究了雪松树冠阻力系数与雷诺数以及孔隙率的关系，而BEREZOVSKAVA等^[27]通过实验、理论以及计算模拟方法分析了树冠与分形的关系。下面分析S_VF，D_f与L_AI之间的关系，然后选择与C_n最相关的无量纲变量。通过分析图4发现：简化模型叶面积指数L_AI与树冠稠密度S_VF成正比，分形维数D_f与树冠稠密度S_VF以及叶面积指数L_AI都成对数关系，本文采用叶面积指数L_AI分析树冠阻力系数C_n，即C_n=f(L_AI)。

3.1  数值模型可靠性验证

为验证数值模型的可靠性，将本文的数值计算结果与其他文献结果进行比较。图5(a)给出了叶面积指数L_AI=8.3(与文献中取值一致)情形下，流域中高度为y/h=1处x方向的速度分布。作为对比，图5(a)中还给出GREEN^[15]和等^[29]的实验结果。由图5(a)可知：空气到达树冠迎风边界前，沿x方向的流速几乎保持与入口处流速相同，在x/h=0处空气流速达到最大值，随后流速迅速降低，在x/h=4.5处流速出现低谷点；此后流速开始回升，并最终保持在某一速度。与其他研究者的结果对比可知：本文给出的树冠迎风区域的风速略高于文献[15]和[29]中的实验风速，但在树冠的下游区域本文数值结果与实验结果吻合较好。图5(b)给出了x/h=1处(树冠下游)，空气沿y方向的平均速度分布。为方便比较，图5(b)中横坐标的速度参量采用其他文献给出的量纲一速度形式，即将实际风速比摩擦速度u*(u*=1.03 m/s)。摩擦速度u*定义如下：

式中：k为冯卡门常数(取0.4)；u_top为树冠顶部速度；Z_top和Z₀分别为树冠高度和参考高度。可以看出：本文的数值结果与文献[16]中的数值结果吻合较好，而文献[4]和[30]中的计算结果均高于本文结果。引起这些误差的原因可能有2个：一是k-ε湍流模型不能详尽模拟树冠周围剧烈变化的湍流分布；二是二维简化树冠与三维真实树冠在模拟树冠内外流场分布的流通截面积上存在偏差。

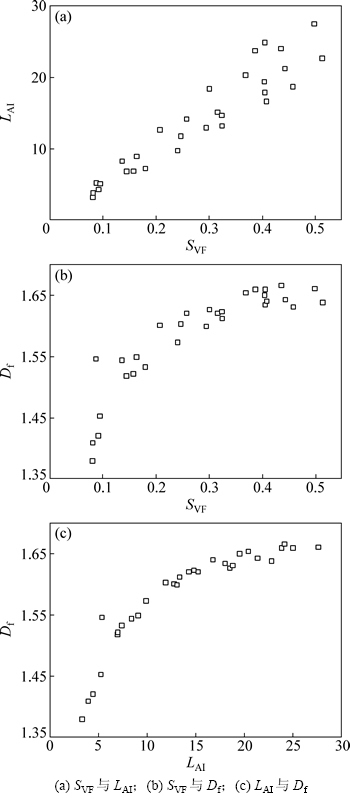
图4  稠密度S_VF、分形维数D_f与叶面积指数L_AI相互关系

Fig. 4  Relationship among solid volume fraction S_VF, fractal dimension D_f and leaf area index L_AI

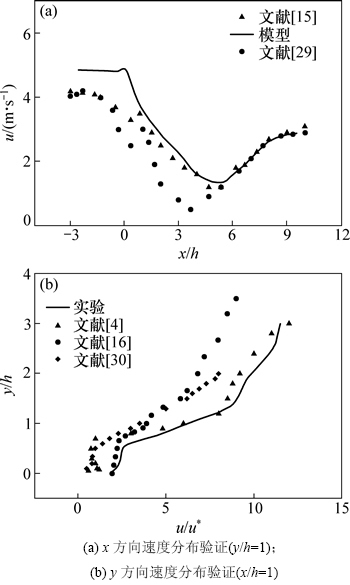
图5  x方向速度分布验证(y/h=1)和y方向速度分布验证(x/h=1)

Fig. 5  Normalized horizontal profiles of streamwise velocity component (y/h=1) and normalized vertical profiles of streamwise velocity component (x/h=1)

上述对比分析结果表明：将三维树冠简化为二维树冠后，并采用标准k-ε模型进行树冠流场模拟虽然存在一定的误差，但仍可获得较为满意的结果。

3.2  树冠流场特性

由于树冠枝叶的阻碍作用，空气流速在树冠内部将降低，伴有明显的速度梯度和压力梯度，并产生剧烈的湍流脉动。选取模拟结果中叶团簇的当量直径D_I=4.84 cm，速度入口u=1 m/s时叶面积指数分别为5.3，8.3，12.7和18.5的4种情形，并与文献[5]和[24]中的模拟结果进行比较，见图6。IRVINE等^[5]的压强分布图表明：来流遇到树冠时静压由0 Pa迅速升高为3.8 Pa，离开树冠时压强由-1.9 Pa迅速回升到0 Pa；GASH^[24]的静压分布图显示风穿过森林时，森林尾部的静压分布为-4.3~0 Pa。而本文模拟结果与文献[5]和[24]中的模拟结果相比：空气流过树冠前后压力梯度分布相似，即气流在遇到树冠时由于树冠的阻力作用风速剧烈衰减，静压升高，并在树冠内部压静压发生转折迅速由正值降为负值，离开树冠时静压迅速回升，但是数值上有一定的差距，静压分布为0~0.6 Pa及-0.6~0 Pa。与文献[5]和[24]中模拟的二维树冠压力分布相比，本文模拟值在绝对值上偏小的原因有：1) 二维树冠简化方式不同，模拟出来的压力分布也不同，在这点上文献[5]和[24]中模拟的尾流压力分布也存在很大差异；2) 文献[5]和[24]中模拟的是二维简化森林边界的流场分布，来流穿过森林前后边界的压力分布和来流穿过单个二维简化树冠肯定是有差别的。此外，由图6可知：在入口风速相同的情况下，随着树冠叶面积密度增加，静压变化的梯度越加明显。

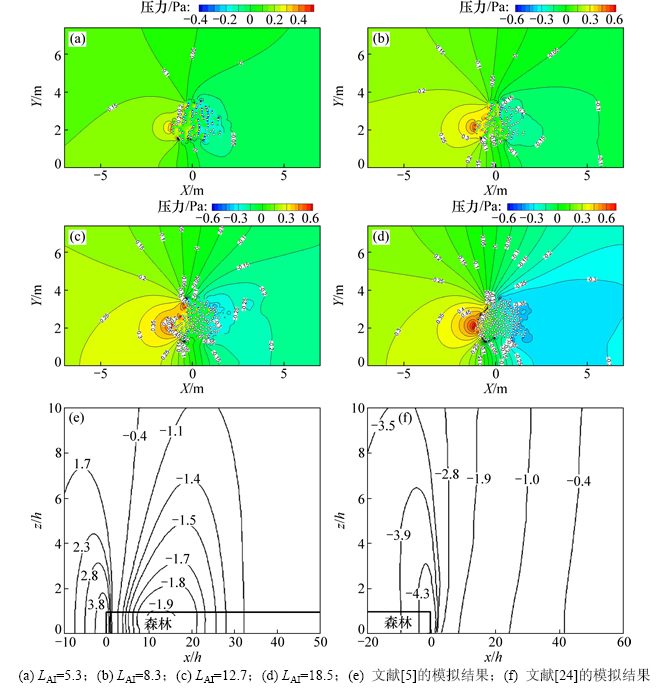
图6  叶团簇的当量直径D_I=4.84 cm，入口速度u=1 m/s时的压力云图

Fig. 6  Pressure contour with diameter of leaf clusters D_I=4.84 cm and inlet velocity u=1 m/s

3.3  树冠阻力系数C_n模型

根据SANZ^[31]提出树冠动量源项S_u：

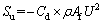            (8)

式中：C_d为阻力系数；ρ为空气密度；A_f为叶面积指数；U为空气平均流速。

树冠阻力的表达式为

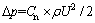             (9)

由此提出树冠阻力系数C_n：

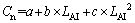         (10)

由于落叶树秋季落叶后形成的树干也会产生流动阻力，故这里包含常数项a，以修正式(8)。将所有的模拟结果拟合得出：

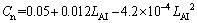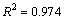，                 (11)

代入式(9)得到：

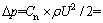
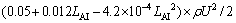 (12)

由式(11)可知：叶面积指数L_AI的二次项系数c相比常数项a和一次项b可以忽略，树冠阻力系数C_n为叶面积指数L_AI的一次函数，即

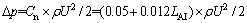    (13)

本文采用4种植物(桂花、竹子、广玉兰和八角金盘)进行实验，每种植物分别取5种叶面积指数进行实验，则可得到20条不同树种不同叶面积指数的压力损失-速度曲线。分别将这20条曲线所对应的叶面积指数L_AI以及速度代入式(13)得出20条模拟曲线。但模拟公式得出的压差偏小，故须乘以修正系数k，即

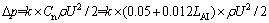 (14)

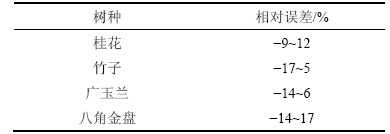
这样得出的模拟结果与实验结果进行对比，结果如图7所示。由图7可知：当模拟公式乘以修正系数k后得出的结果与实验结果十分吻合。其中经过修正的拟合公式代入各树种的参数后和风洞试验所得结果误差见表2。则树冠阻力系数C_n可修正为C′_n：

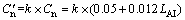       (15)

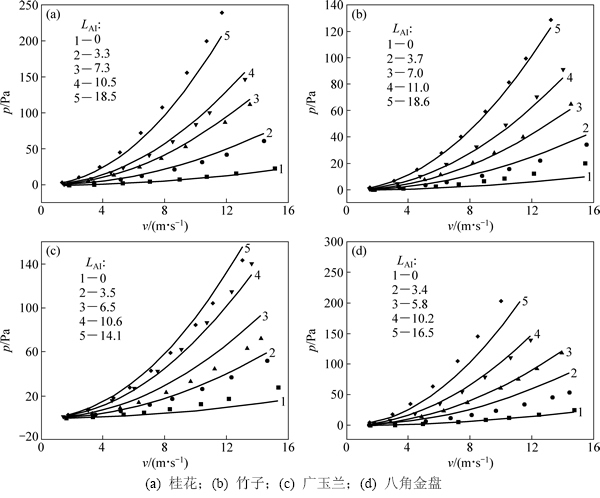
图7  实验数据与经过修正的拟合结果对比

Fig. 7  Comparison of modified simulation results and measured results

表2  经过修正的拟合公式所得结果与实验结果误差评估

Table 2  Error evaluation between results obtained by improved simulation expression and experimental results

4  结论

1) 为深入分析树冠内部结构参数对树冠绕流流动阻力的影响，将三维复杂树冠简化为二维简化树冠模型并提出相关树冠结构参数叶面积指数L_AI、稠密度S_VF以及分形维数D_f。采用数值模拟和实验测试相结合的方法研究几种典型形态特征树冠的内部流场特征和流动阻力。用树冠叶面积指数(L_AI)、稠密度(S_VF)和分形维数(D_f)表征树冠复杂的形态结构，讨论了树冠形态结构参数对树冠流动阻力的影响规律。

2) 通过与文献值对比，可以验证简化树冠水平方向(x方向)速度分布与文献中的实验速度及模拟速度较吻合；简化树冠高度方向(y方向)的平均速度分布曲线与其他模拟结果及文献中的实验结果相比一致性高。

3) 在简化树冠的基础上提出树冠阻力模型△p=C_n×ρU²/2，并假设树冠阻力系数C_n是模型树冠结构参数稠密度S_VF、分形维数D_f及叶面积指数L_AI的函数，即C_n=f(S_VF，D_f，L_AI)，通过分析发现简化模型叶面积指数L_AI与树冠稠密度S_VF成正比，分形维数D_f与树冠稠密度S_VF以及叶面积指数L_AI都成对数关系。

4) 采用叶面积指数L_AI分析树冠阻力系数C_n，进而引出树冠阻力系数模型C_n=a+b×L_AI+c×L_AI²。通过将模拟结果拟合分析得出关于树冠阻力系数C_n的模型公式：C_′n=k×C_n=k×(0.05+0.012L_AI)。

参考文献：

[1] CAO Jinxin, TAMURA Y, YOSHIDA A. Wind tunnel study on aerodynamic characteristics of shrubby specimens of three tree species[J]. Urban Forestry & Urban Greening, 2012, 11: 465-476.

[2] SANZ R J, van BEECK J, DEZSO W G. Wind tunnel simulation of the wind conditions inside bidimensional forest clear-cuts. Application to wind turbine siting[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2007, 95: 609-634.

[3] MOLINA-AIZ F D, VALERA D L, ALVAREZ A J, et al. A wind tunnel study of airflow through horticultural crops: determination of the drag coefficient[J]. Biosystems Engineering, 2006, 93(4): 447-457.

[4] DUMAN T, KATUL G G, SIQUEIRA M B, et al. A velocity–dissipation lagrangian stochastic model for turbulent dispersion in atmospheric boundary-layer and canopy flows[J]. Boundary Layer Meteorology, 2014, 152: 1-18.

[5] IRVINE M R, GARDINER B A, HILL M K. The evolution of turbulence across a forest edge[J]. Boundary Layer Meteorology, 1997, 84(3): 467-496.

[6] NOVAK M D, WARLAND J S, ORCHANSKY A L, et al. Wind tunnel and field measurements of turbulent flow in forests. Part I: uniformly thinned stands[J]. Boundary Layer Meteorology, 2000, 95(3): 457-495.

[7] 关德新, 朱廷耀. 树冠结构参数及附近风场特征的风洞模拟研究[J]. 运用生态学报, 2000, 11(2): 202-204.

GUAN Dexin, ZHU Tingyao. Wind tunnel experiment on canopy structural parameters of isolated tree and wind velocity field characters nearby[J]. Chinese Journal of Applied Ecology, 2000, 11(2): 202-204.

[8] ZENG P, TAKAHASHI H. A first-order closure model for the wind flow within and above vegetation canopies[J]. Agricultural and Forest Meteorology, 2000, 103: 301-313.

[9] SIQUEIRA M, KATUL G, TANNY J. The effect of the screen on the mass, momentum, and energy exchange rates of a uniform crop situated in an extensive screen house[J]. Boundary Layer Meteorology, 2012, 142(3): 339-363.

[10] SOGACHEV A, PANFEROV O. Modification of two-equation models to account for plant drag[J]. Boundary Layer Meteorology, 2006, 121(2): 229-266.

[11] SOGACHEV A. A note on two-equation closure modelling of canopy flow[J]. Boundary Layer Meteorology, 2009, 130(3): 423-435.

[12] MOCHIDA A, TABATA Y, IWATA T, et al. Examining tree canopy models for CFD prediction of wind environment at pedestrian level[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96: 1667-1677.

[13] HIRAOKA H, OHASHI M. A (k-ε) turbulence closure model for plant canopy flows[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96: 2139-2149.

[14] 李亮, 李晓峰, 林波荣, 等. 用带k-ε源项两方程湍流模型模拟树冠流[J]. 清华大学学报(自然科学版), 2006, 46(6): 753-756.

LI Liang, LI Xiaofeng, LIN Borong, et al. Simulation of canopy flows using k-ε two-equation turbulence model with source/sink terms[J]. Journal of Tsinghua University (Science and Technology), 2006, 46(6): 753-756.

[15] GREEN S R. Modeling turbulent air flow in a stand of widely spaced trees[J]. Phoenics, 1992, 23: 294-312.

[16] HUANG J, CASSIANI M, ALBERTSON J D. Coherent turbulent structures across a vegetation discontinuity[J]. Boundary Layer Meteorology, 2011, 140: 1-22.

[17] DUPONT S, BRUNET Y. Edge flow and canopy structure: a large-eddy simulation study[J]. Boundary Layer Meteorology, 2008, 126: 51-71.

[18] DUPONT S, BRUNET Y. Influence of foliar density profile on canopy flow: a large-eddy simulation study[J]. Agricultural and Forest Meteorology, 2008, 148: 976-990.

[19] PATTON E G, KATUL G G. Turbulent pressure and velocity perturbations induced by gentle hills covered with sparse and dense canopies[J]. Boundary Layer Meteorology, 2009, 133: 189-217.

[20] YANG B, RAUPACH M R, SHAW R H, et al. Large-eddy simulation of turbulent flow across a forest edge. Part I: flow statistics[J]. Boundary Layer Meteorology, 2006, 120(3): 377-412.

[21] SCHLEGEL F, STILLER J, BIENERT A, et al. Large-eddy simulation of inhomogeneous canopy flows using high resolution terrestrial laser scanning data[J]. Boundary Layer Meteorology, 2012, 142(2): 223-243.

[22] BELCHER S E, HARMAN I N, FINNIGAN J J. The wind in the willows: flows in forest canopies in complex terrain[J]. Annual Review of Fluid Mechanics, 2012, 44(1): 479-504.

[23] SVENSSON U, HAGGKVIST K. A two-equation turbulence model foor canopy flows[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1990, 35: 201-211.

[24] GASH J H C. Observations of turbulence downwind of a forest-heath interface[J]. Boundary Layer Meteorology, 1986, 36(3): 227-237.

[25] LAUNDER B E, SPALDING D B. The numerical computation of turbulent flows[J]. Computer Methods in Applied Mechanics and Engineering, 1974, 3: 269-289.

[26] VERSTEEG H K, MALALASEKERA W. An introduction to computational fluid dynamics[M]. Englewood Cliffs, NJ: Prentice-Hall, 1995: 82.

[27] BEREZOVSKAVA F S, KAREV G P, KHLEBOPROS R G, et al. A fractal approach to computer analytical modelling of tree crowns[J]. Trees, 1997, 11: 323-327.

[28] GRANT P F, NICKLING W G. Direct field measurement of wind drag on vegetation for application to windbreak design and modelling[J]. Land Degradation & Development, 1998, 9: 57-66.

[29] S, KUILE B T. Modelling and simulations of turbulent flows in urban areas with vegetation[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2013, 123: 43-45.

[30] REYNOLDS A M. Development and validation of a lagrangian probability density function model of horizontally-homogeneous Turbulence within and above plant canopies[J]. Boundary Layer Meteorology, 2012, 142: 193-205.

[31] SANZ C. A note on k-ε modelling of vegetation canopy air-flows[J]. Boundary Layer Meteorology, 2003, 108: 191-197.

(编辑  杨幼平)

收稿日期：2015-12-28；修回日期：2016-03-09

基金项目(Foundation item)：国家自然科学基金资助项目(41371445)(Project(41371445) supported by the National Natural Science Foundation of China)

通信作者：付海明，博士，高级工程师，从事空气过滤净化与空气品质研究；E-mail：fhm@dhu.edu.cn