DOI: 10.11817/j.issn.1672-7207.2015.02.046
组合式吸液芯内液态金属钠流动特性的数值模拟
于萍1,2,张红1,3,许辉1,沈妍1,白穜1
(1. 南京工业大学 能源学院,江苏 南京,211816;
2. 徐州工程学院 机电工程学院,江苏 徐州,221000;
3. 常州工学院,江苏 常州,213002)
摘要:为进一步了解高温热管工作时工质钠的流动和分布情况,用有限容积法和Darcy理论数值模拟二级学院组合式吸液芯内液态金属钠的流动特性,根据模拟结果对液态金属钠流经组合式吸液芯的压力降、分布均匀程度、湍流动能和湍流耗散率进行分析。研究结果表明,随着液态金属钠的进口流速增大和组合式吸液芯中金属纤维毡厚度增大,液态金属钠在组合式吸液芯内的速度分布越不均匀;随着组合式吸液芯中金属纤维毡厚度减小,液态金属钠在其中的湍流动能和湍流耗散率越大;液态金属钠通过组合式吸液芯的压降随着进口流速的增大而增大,且进口流速相同时,液态金属钠经过金属纤维毡厚度越大的组合式吸液芯的压降越大。压降的数值模拟值与实验值的最大相对误差约为6.8%,说明本文数值模型的正确性。
关键词:液态金属;组合式吸液芯;流体分布;湍流耗散率;湍流动能
中图分类号:TK172 文献标志码:A 文章编号:1672-7207(2015)02-0715-08
Simulation for liquid sodium flow characteristics through combined wick
YU Ping1,2, ZHANG Hong1,3, XU Hui1, SHEN Yan1, BAI Tong1
(1. College of Energy, Nanjing University of Technology, Nanjing 211816, China;
2. School of Mechanical and Electrical Engineering, Xuzhou Institute of Technology, Xuzhou 221000, China
3. Changzhou Institute of Technology, Changzhou 213002, China)
Abstract: In order to further study the flow and distribution of liquid sodium in the high temperature heat pipe, flow characteristics of liquid sodium in the combined wick were simulated numerically using the finite volume method and Darcy model. The pressure drop, uniformity degree of velocity distribution, turbulent kinetic energy, and turbulent dissipation rate were analyzed according to the simulated results. The results show that the fluid velocity distribution in the combined wick gets more uneven with the increase of the inlet velocity of liquid sodium and the thickness of metal fiber felt. The less thickness of the metal fiber felt in the combined wick, the greater the turbulent kinetic energy and the turbulent dissipation rate of liquid sodium. The pressure drop of liquid sodium through the combined wick increases with the increase of inlet velocity. And when the same inlet velocity is applied, the pressure drop of liquid sodium through the combined wick gets greater with the increase of the metal fiber felt. The maximum relative error of pressure drop between simulated value and experimental value is about 6.8%, which explains that the numerical model is correct.
Key words: liquid metal; combined wick; fluid distribution; turbulent dissipation rate; turbulent kinetic energy
热管是一种高效传热元件,具有高的导热性、理想的等温性、热流密度的可调性以及传热方向的可逆性等优点。热管凭借其自身独特的优势,目前被广泛地应用于太阳能热利用方面[1-5]。具有毛细结构的吸液芯多孔介质决定了热管的传热性能,因此,热管内多孔介质吸液芯内的流动与传热机理已成为研究热点。Wang等[6]采用烧结的铜丝网作为热管吸液芯,分析了铜丝网的数量、直径和层数,以及热管倾斜角度对热管传热能力的影响。研究发现:热管最大换热能力时吸液芯的铜丝直径为1.2 mm左右。Xiao等[7]设计了一种复合吸液芯,在铜丝网上烧结上球形的铜粉和丝状的镍粉、烧结的金属粉末可以提供大毛细抽力,而铜丝网作为低阻力的流动通道。试验结果表明:采用此种吸液芯的热管的当量导热系数是吸液芯为铜丝网的热管的5倍左右。白穜等[8]设计了一种热管内组合式吸液芯,使吸液芯同时具有高毛细力、低流动阻力及强化传热等特点,研究了组合式吸液芯的毛细力、流动阻力和传热特性,并用控制容积法数值模拟了工质水在组合式吸液芯中的流动情况,结果与实验值吻合较好。文献[8]中组合式吸液芯的应用背景是高温热管,但只研究了工质水在组合式吸液芯内的特性,并没有对液态金属钠在组合式洗液芯内的流动特性进行进一步研究,液态金属钠具有较低的黏度和较大的表面张力系数,与水的物性参数存在一定差异,因此,以液态金属钠为研究对象考查组合式吸液芯内的流动特性具有重要意义。通过研究液态金属钠在组合式吸液芯内的流动特性,可获得液态金属钠在组合式吸液芯内的分布和流动情况,全面了解高温热管的工作过程,对高温热管的性能研究提供参考依据。本文作者建立数学模型,对液态金属钠在组合式吸液芯内的流动特性进行进一步研究。根据模拟结果将对组合式吸液芯内流体的压降、速度场、湍流动能、湍流耗散率以及模型出口的速度的标准偏差进行分析。
1 数学物理模型
1.1 物理模型
组合式吸液芯的结构示意图如图1所示。在热管内壁上直接线切割出三角沟槽,上面覆盖一层未烧结的金属纤维毡,然后用一层大孔径的金属丝网将其固定。热管外径为32 mm,壁厚为3 mm,长为70 mm;三角沟槽的槽宽和槽深均为0.8 mm,数量为110个。以未经烧结的金属纤维毡为基础,将固定厚度的金属纤维毡不断的覆盖从而得到相应的厚度,厚度越大则压缩程度越大,组合式吸液芯的渗透率越小。具体情况参照文献[9]。不同厚度的金属纤维毡的组合式吸液芯的渗透率见表1。
表1 物理模型参数表
Table 1 Parameter of physical model
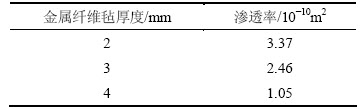
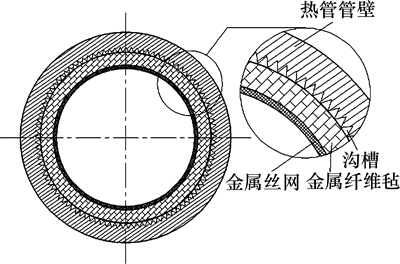
图1 物理模型
Fig. 1 Physical model
1.2 数学模型
1.2.1 数学模型成立的假设条件
三维模型的假设条件为1) 流动为稳定流动;2) 不考虑重力的影响;3) 流体和组合式吸液芯的物性为常数。
1.2.2 控制方程
多孔介质内动量损失包括2部分:黏性损失项和惯性损失项。
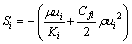 (1)
(1)
式中:i代表x,y,z方向;Si为动量源项;μ为流体的动力黏度;ui为流体的流速标量;Ki为多孔介质的渗透率;ρ为流体的密度;Cfi为流体惯性阻力系数。Darcy定律适用于流体处于低雷诺数流动时,压力梯度主要用来克服黏性阻力;而当流体速度逐渐增加时,惯性力的影响逐渐明显,此时,压力梯度和流体速度之间的关系可以用Darcy-Forchheimer定律来描述。根据Darcy定律,当多孔介质内的流体处于层流状态时,动量损失项中黏性损失项和流体的速度成正比,惯性阻力系数Cfi为0。根据Darcy-Forchheimer定 律[10-11],多孔介质内湍流流动的动量方程与层流状态时相比,多了由于考虑惯性阻力效应而增加的源项。
根据假设条件,层流时数学模型的控制方程包括质量守恒方程和动量守恒方程:
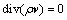 (2)
(2)
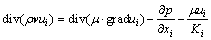 (3)
(3)
式中:v为速度矢量;p为压力。当流体处于湍流状态时,采用Reynolds平均法[12],用k-ε两方程模型,其控制方程包括连续性方程、动量方程以及k和ε方程。其中k方程为湍流动能方程,ε方程为求解湍流耗散率的方程。
动量守恒方程:
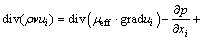

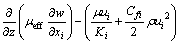 (4)
(4)
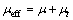 (5)
(5)
k方程:
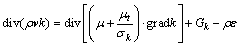 (6)
(6)
ε方程:
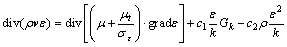 (7)
(7)
Gk表示由于平均速度梯度而引起的湍流动能k的产生项,
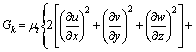
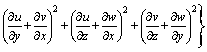 (8)
(8)
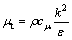 (9)
(9)
式中:μt为湍流黏度;k为湍流动能;ε为湍流耗散率;cm,c1和c2为经验常数;σk和σε分别为与湍动能和湍流耗散率对应的Prandtl数。各系数取值分别为: cm=0.09,c1=1.44,c2=1.92,σk=1.00,σε=1.30[13]。
1.3 数值模型
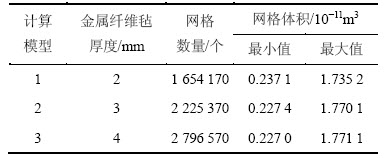
数值计算的流体区域包括2部分:流域1为所有三角沟槽的集合,流域2为金属纤维毡的圆环区域,如图2和图3所示。因为金属纤维毡的厚度(δ)分别为2,3和4 mm,所以建立的计算模型有3个,对应的网格数量和尺寸见表2。将组合式吸液芯分块划分网格,对所有三角沟槽流域使用非结构四面体网格,对金属纤维毡区域使用六面体结构网格。数值模型的进口采用速度入口边界条件,指定进口边界上各节点的速度,出口为自由出流边界条件。采用控制容积法对方程进行离散,离散方法选择二阶迎风格式,速度和压力的耦合方法采用SIMPLE算法。为了使三角沟槽流体区域和金属纤维毡流体区域之间重合的界面上的量能进行插值传递,即有流体在此交界面通过,交界面采用正则网格。

图2 组合式吸液芯流域
Fig. 2 Flow area of combined wick
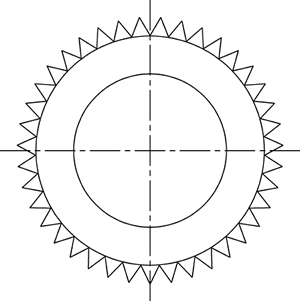
图3 组合式吸液芯横截面示意图
Fig. 3 Schematic cross-section of combined wick
表2 网格数量和体积
Table 2 Parameters of grid
1.4 参数求解
液钠的流动状态根据雷诺数Re进行判定:
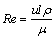 (10)
(10)
式中:u为流体速度;μ为流体的动力黏度;ρ为流体密度;l为特征尺寸。本文计算流域包括金属纤维毡和三角沟槽2个区域,结构不同特征尺寸不同,因此,要对这2个区域分别判定流动状态。
对于金属纤维毡吸液芯,Dullien[14]的研究表明,纤维材料的特征尺寸为纤维丝的平均直径dw,当Re<1时,金属纤维毡内流体为层流状态,当Re>1时,金属纤维毡内流体为湍流状态。
对于三角沟槽吸液芯,可将其内部的流动看成是横截面为三角沟槽的圆环流动,雷诺数的判定值为2 300。三角沟槽的特征尺寸即为水力直径d:
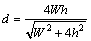 (11)
(11)
其中,W为槽宽;h为槽深。
当三角沟槽和金属纤维毡内的流动均为层流状态时,认为组合式吸液芯内的流动状态为层流,其余情况均认为流动状态为湍流状态。
为了表征流体在组合式吸液芯内的分布均匀情况,使用Bessel公式[15],计算出组合式吸液芯计算模型的出口速度标量的标准偏差σ:
 (12)
(12)
式中:uj为各节点的速度;j=1,2,3,…,n;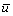 为速度的平均值。湍流动能是指单位质量的流体由于湍流脉动而具有的动能,表征了流体湍流扰动的剧烈程度。由此可知,湍流动能主要来源于湍流脉动,通过雷诺切应力做功给湍流流体提供能量。
为速度的平均值。湍流动能是指单位质量的流体由于湍流脉动而具有的动能,表征了流体湍流扰动的剧烈程度。由此可知,湍流动能主要来源于湍流脉动,通过雷诺切应力做功给湍流流体提供能量。
湍流耗散率是指在分子黏性力作用下由湍流动能转化为分子热运动动能的速率,是脉动黏性应力与脉动应变率的乘积。通过对湍流耗散率的研究可以了解流体运动中的能量损失以及运动的规律,进而可以为试验装置的改进以及优化提供帮助和参考。
2 结果和讨论
2.1 模型验证
为了验证模型的正确性,本文分别数值模拟了工质水流过δ分别为2,3和4 mm的组合式吸液芯的情况,得到了流动压降。图4和图5所示分别为模拟值和文献[9]中的实验值和模拟值的压降对比情况。由图4和5可知,当组合式吸液芯内部流体分别为层流状态和湍流状态时,本文中的模拟值和文献[9]中实验值的最大相对误差为6.8%,从而证明了本文数值模型的正确性。
因为渗透率是多孔介质结构的参数,惯性阻力系数是雷诺数和纤维毡厚度的函数,这些函数的变量都与流体的物性无关,所以用同一数值模型模拟高温钠液在不同厚度金属纤维毡的组合式吸液芯内的流动是可行的。本文选取温度1 000 K时的饱和液钠作为模型中的流动介质,其基本物性参数为:密度ρ= 778 kg/m3,动力黏度μ=1.809×10-4 Pa·s,表面张力σ=0.132 N/m。

图4 层流压降比较
Fig. 4 Comparison of pressure in laminar state

图5 湍流压降比较
Fig. 5 Comparison of pressure in turbulent state
2.2 流速和压降的关系
在层流状态下,液钠在不同厚度下的金属纤维毡的组合式吸液芯中进口流速与压降呈线性关系。层流状态下流速和压降的关系和湍流状态下流速和压降的关系如图6和图7所示。从图6和图7可知:压降随着流速的增大而增大,且进口流速相同时,δ越大的组合式吸液芯的压降越大。数值模拟值和公式计算值的相对误差最大约为6.5%,模拟值和理论值吻合良好,说明可以利用数值模拟很好地预测组合式吸液芯内的流动特性,进而为设计热管提供一定的依据。
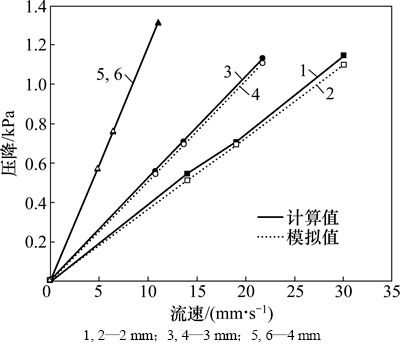
图6 层流状态下流速和压降的关系
Fig. 6 Relationship between velocity and pressure differences under laminar state

图7 湍流状态下流速和压降的关系
Fig. 7 Relationship between velocity and pressure differences under turbulence state
在湍流状态下不仅要考虑黏性力的作用,还要考虑惯性力的作用,因此,流体流经组合式吸液芯时,压降增加,且进口流速越大,惯性力的影响越明显。当δ分别为2,3和4 mm,进口流速从50 mm/s增加到82 mm/s时,惯性力产生的压降占流体流经组合式吸液芯时所产生的总压降的比例分别增加约21.22%,48.88%和41.07%。在进口流速相同的情况下,δ为4 mm的组合式吸液芯的压降最大。这是因为本文以未烧结的金属纤维毡为基础,将压缩后的金属纤维毡不断覆盖得到相应厚度,因此,厚度越大,纤维毡的压缩程度越大,金属纤维毡内部流体通道重新排列,渗透率减小,流体在其中的流动阻力增大。
2.3 结构和三角沟槽内液钠流量的关系
图8所示为当液钠进口流速为19 mm/s时,δ为2 mm的组合式吸液芯出口横截面速度分布。从图8可以看出,三角沟槽内液态金属钠的流速比金属纤维毡内的流速大,说明三角沟槽主要提供了流动通道的作用,而金属纤维毡主要提供大的毛细抽力。

图8 金属纤维毡厚2 mm的组合式吸液芯横截面速度分布情况
Fig. 8 Velocity distribution of cross section of combined wick with 2 mm metal fiber felt
图9所示为流过三角沟槽的液态金属钠的体积分数随组合式吸液芯中δ的变化情况。由图9可知:在进口液钠流量相同的情况下,δ为2 mm的组合式吸液芯,约有42.82%的液钠从三角沟槽通道流过;δ为4 mm的组合式吸液芯,约有40.72%的液钠从三角沟槽通道内流过。δ越大,渗透率越小,阻力越大,但是δ增大,其对应的流动通道的横截面积也变大,所以,有更多的液钠从金属纤维毡流过。组合式吸液芯将管芯分为2部分:一部分起到毛细抽力作用,另一部分起到液体回流通道作用。三角沟槽的存在减小了流体流经组合式吸液芯的压降。与δ为4 mm的组合式吸液芯的相比,对δ为2 mm的组合式吸波芯中通过三角沟槽的液态金属钠增加了2.1%,因为三角沟槽的渗透率比金属纤维毡的大,所以,组合式吸液芯的流动阻力随着δ减小而减小。由此可知:组合式吸液芯中金属纤维毡厚度越小(即金属纤维毡的压缩程度越小)越好。
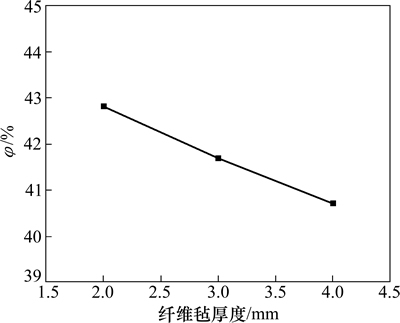
图9 金属纤维毡厚度不同的组合式吸液芯中流过三角沟槽的液钠
Fig. 9 Ratio of liquid sodium flowing through groove in combined wick with different thicknesses of metal fiber felt
2.4 进口流速和流体速度分布均匀程度的关系
组合式吸液芯内流体速度分布的均匀程度用速度标量的标准偏差(σ)表征。σ越大,说明各点的速度标量偏离平均速度越大,流体速度分布越不均匀;反之,则说明流体速度分布越均匀。
图10所示为层流状态和湍流状态时进口流速和出口处σ的关系。由图10可知,在层流状态下,进口流体速度和σ呈成线性关系;在湍流状态下,进口流速增大σ也增大;当进口流速从82 mm/s增加到115 mm/s时,δ分别为2,3和4 mm的组合式吸液芯的σ分别增加了31.57%,38.83%和39.51%;当进口流速从115 mm/s增加到148 mm/s时,δ分别为2,3和4 mm的组合式吸液芯的σ分别增加了26.29%,28.10%和28.27%。
2.5 结构和流体速度分布的关系
由图10可知:当进口速度为15 mm/s时,金属纤维毡厚度为3 mm厚的组合式吸液芯的σ比2 mm厚的大31.18%,4 mm厚的组合式吸液芯的σ比3 mm厚的大15.66%;当进口流速为115 mm/s时,3 mm厚的组合式吸液芯的σ比2 mm的大28.30%,4 mm厚的金属纤维毡的组合式吸液芯的σ比3 mm厚的大14.84%。另外,层流状态时,金属纤维毡的厚度越大,σ的变化受进口流速的影响越大。
从以上可知:进口流速越大,组合式吸液芯内的流体速度分布越不均匀。在进口流速相同的情况下,δ越大的组合式吸液芯内的流体速度分布越不均匀。流体速度分布不均匀,导致流体撞击吸液芯骨架的应力分布不均,因此,金属纤维毡厚度越小(即金属纤维毡压缩程度越小)越好。
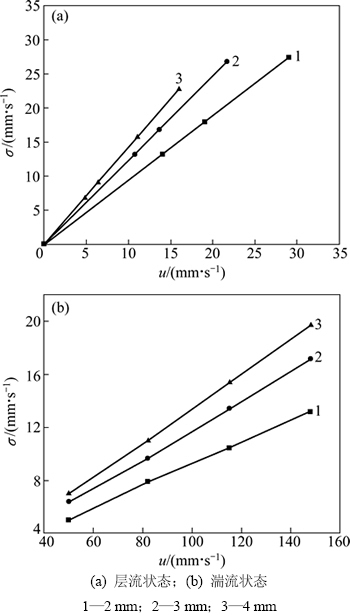
图10 进口流速u和出口速度标量的标准偏差σ的关系
Fig. 10 Relationship between u and σ
2.6 进口流速与径向截面流体的湍流动能和湍流耗散率的关系
因为δ为2,3和4 mm的组合式吸液芯的径向截面的湍流动能和湍流耗散率的分布情况相似,所以,只讨论δ为2 mm的情况。图11和12所示为进口流速不同时δ为2 mm的组合式吸液芯的径向截面的湍动能和湍流耗散率的分布情况。
由图11可知,越靠近模型的进出口湍动能越大,越靠近模型中间,湍动能趋于稳定。这是由于越靠近模型的进出口流体的扰动越剧烈,流固相互作用强烈。在z=40 mm的径向截面上,进口流速为148 mm/s时的湍流动能是进口流速为82 mm/s时的1.65倍左右,说明进口流速越大,湍流动能越大,液钠经过组合式吸液芯时扰动的越剧烈,流固相互作用的越强烈。
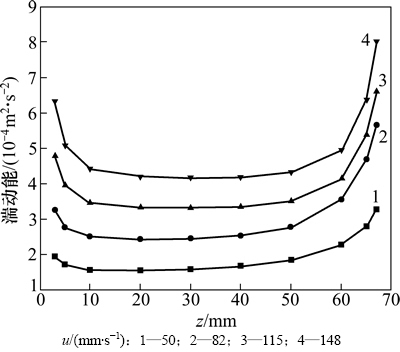
图11 径向截面湍流动能分布
Fig. 11 Distribution of turbulent kinetic energy in radial section

图12 径向截面湍流耗散率分布
Fig. 12 Distribution of turbulent dissipation rate in radial section
由图12可知:越靠近模型的进出口湍流耗散率越大,越靠近模型中间,湍流耗散率趋于稳定。这是由于越靠近模型的进出口,在分子黏性力作用下湍流动能转化为分子热运动动能的速率越大;在Z=40 mm的径向截面上,进口流速为148 mm/s时的湍流耗散率是进口流速为82 mm/s时的2.17倍左右,说明进口流速越大,湍流耗散率越大,液钠流经组合式吸液芯时流体的湍流动能转化成热能的速率越大,能量耗散越严重。
2.7 结构与湍动能和湍流耗散率的关系
图13和图14分别是进口流速为148 mm/s时,δ不同的组合式吸液芯的径向截面流体的湍流动能和湍流耗散率的分布情况。由图13和14可知:当Z=30 mm时,δ=2 mm的组合式吸液芯的湍流动能约为δ=3 mm的1.35倍,为δ=4 mm的1.67倍。δ=2 mm的组合式吸液芯的湍流耗散率约为δ=3 mm的1.34倍,约为δ=4 mm的1.65倍。说明δ越小的组合式吸液芯,其内部的流体和固体的相互作用越剧烈,流体在流动过程中能量损失越严重。若考虑到液态金属钠和吸液芯骨架对流换热,δ越小则流固相互作用越剧烈,对流换热效果越好。但δ越小,湍流耗散率越大,液态金属钠在流动过程中动能损失越严重,所以,在选择δ厚度时,要综合以上因素多方面考虑。
从图13和14还可以发现:δ不同的组合式吸液芯的湍流耗散率和湍流动能在出口处相差不大,这说明在模型的出口处流体扰动剧烈,在分子黏性力作用下,湍流动能转化为分子热运动动能的速率也快速增大。

图13 u=148 mm/s时,径向截面的湍流动能分布
Fig. 13 Distribution of turbulent kinetic energy in radial section with u=148 mm/s

图14 u=148 mm/s时,径向截面的湍流耗散率分布
Fig. 14 Distribution of turbulent dissipation rate in radial section with u=148 mm/s
3 结论
1) 液态金属钠流经组合式吸液芯的压降随着入口速度和δ的增大而增大。所以金属纤维毡的厚度越小(即金属纤维毡的压缩程度越小)的组合式吸液芯的流动阻力越小。
2) 入口液钠速度越大,δ越大,组合式吸液芯内流体速度分布越不均匀,导致流体撞击吸液芯骨架的应力分布不均。
3) 随着组合式吸液芯中δ减小,流过三角沟槽的液态金属钠的体积分数增加。当进口液钠流量相同时, 与4 mm厚的组合式吸液芯相比,2 mm厚的组合式吸液芯中,通过三角沟槽的液态金属钠增加了2.1%。三角沟槽的渗透率比金属纤维毡的大,所以组合式吸液芯的流动阻力随着δ减小而减小。因此,组合式吸液芯中金属纤维毡厚度越小(即金属纤维毡的压缩程度越小)越好。
4) 流体的湍流动能和湍流耗散率在模型进出口处增大。当进口流速为148 mm/s,z=30 mm时,δ=2 mm的组合式吸液芯的湍流动能约为δ=4 mm的1.67倍,其湍流耗散率约为δ=4 mm的1.65倍。说明δ越小的组合式吸液芯,其内部的流体和固体的相互作用越剧烈,流体在流动过程中能量损失越严重。考虑液态金属钠和吸液芯骨架对流换热,δ越小则流固相互作用越剧烈,对流换热效果越好;但δ越小,湍流耗散率越大,液态金属钠在流动过程中动能损失越严重。
5) 当组合式吸液芯中的金属纤维毡厚度较小时,具有流动阻力小、流体速度分部均匀、流固对流换热效果好等优点;但是金属纤维毡厚度越大,毛细抽力越大,金属纤维毡可以提供更多的有效汽化核心,提高了传热效果。所以,组合式吸液芯中δ的选择要综合以上因素根据需要多方的考虑。
参考文献:
[1] Chung H S, Woo J S, Shin Y H, et al.Experimental assessment of two-phase bubble pump for solar water heating[J]. Journal of Central South University, 2012, 19(6): 1590-1599.
[2] 丁莉, 张红, 许辉, 等. 太阳能接收器中高温热管等温及导热性能的试验研究[J]. 热力发电, 2010, 39(3): 40-48.
DING Li, ZHANG Hong, XU Hui, et al. Test study on isothermal and heat-conducting performance of high-temperature heat pipe in solar energy receiver[J]. Thermal Power Generation, 2010, 39(3): 40-48.
[3] 许辉, 张红, 白穜, 等. 高温热管太阳能接收器的开发及传热特性分析[J]. 太阳能学报, 2010, 31(12): 1585-1590.
XU Hui, ZHANG Hong, BAI Tong, et al. Development and heat transfer analysis of high temperature heat pipe solar receiver[J]. Acta Energiae Solaris Sinica, 2010, 31(12): 1585-1590.
[4] Baturkin V, Andraka C, Zaripov V. Features of fabrication technology and properties of wicks of heat pipe receiver for solar dish/stirling systems[C]//International Solar Energy Conference. Orlando: American Society of Mechanical Engineers, 2005: 679-685.
[5] Andraka C E, Rawlinson K S, Moss T A. Solar heat pipe testing of the stirling thermal motors 4-120 stirling engine[C]// Proceedings of the 31th Intersociety Energy Conversion Engineering Conference. Washington DC, 1996: 1295-1300.
[6] WANG Yaxiong, Peterson G P. Analysis of wire-bonded micro heat pipe arrays[J]. Journal of Thermophysics and Heat Transfer, 2002, 16(3): 346-355.
[7] XIAO Huang, Franchi G. Design and fabrication of hybrid bi-modal wick structure for heat pipe application[J]. Journal of Porous Materials, 2008, 15(6): 635-642.
[8] 白穜, 张红, 许辉, 等. 一种新型组合式热管吸液芯性能的研究[J]. 中国电机工程学报, 2011, 31(23): 79-85.
BAI Tong, ZHANG Hong, XU Hui, et al. Performance study on a novel combined wick of heat pipe[J]. Proceeding of the CSEE, 2011, 31(23): 79-85.
[9] 白穜, 张红, 许辉, 等. 流体在组合式吸液芯中的流动阻力[J]. 南京工业大学学报(自然科学版), 2012, 34(1): 56-60.
BAI Tong, ZHANG Hong, XU Hui, et al. Investigations of flow resistance through combined heat pipe wick[J]. Journal of Nanjing University of technology (Natural Science Edition), 2012, 34(1): 56-60.
[10] Wu W T, Liu J F, Li W J, et al. Measurement and correlation of hydraulic resistance of flow through woven metal screens[J]. International Journal of Heat and Mass Transfer, 2005, 48(14): 3008-3017.
[11] Liu J F, Wu W T, Chiu W C, et al. Measurement and correlation of friction characteristic of flow through foam matrixes[J]. Experimental Thermal and Fluid Science, 2006, 30: 329-336.
[12] 张帅帅. 计算流体动力学及其应用—CFD软件的原理及应用[M]. 武汉: 华中科技大学出版社, 2007: 77-88.
ZHANG Shuaishuai. Computational fluid dynamics and application: The principle and application of CFD software[M]. Wuhan: Huazhong University of Science and Technology Press, 2011: 77-88.
[13] 陶文铨. 数值传热学[M]. 西安: 西安交通大学出版社, 2001: 436-437.
TAO Wenquan. Numerical heat transfer[M]. Xi’an: Xi’an Jiaotong University Press, 2001: 436-437.
[14] Dullien F A L. Porous media: Fluid transport and pore structure[M]. San Diego: Academic Press, 1992: 211-213.
[15] 邢桂菊, 黄素逸. 热工实验原理和技术[M]. 北京: 冶金工业出版社, 2007: 6-8.
XING Guiju, HUANG Suyi. Thermal experimental principle and technology[M]. Beijing: Metallurgy Industry Press, 2007: 6-8.
(编辑 赵俊)
收稿日期:2014-02-10;修回日期:2014-04-15
基金项目(Foundation item):国家自然科学基金资助项目(51076062);江苏省高校研究生科研创新计划项目(CXZZ12_0421)(Project (51076062) supported by the National Natural Science Foundation of China; Project (CXZZ12_0421) supported by the University Graduated Student Research Innovation Plan Program of Jiangsu Province)
通信作者:张红,教授,博士生导师,从事先进能源领域的高效传热传质设备技术研究;E-mail:hzhang@njut.edu.cn