基于分层假定入渗模型的边坡安全性分析
张杰1, 2,韩同春1, 2,豆红强1, 2,马世国1, 2
(1. 浙江大学 浙江大学滨海和城市岩土工程研究中心,浙江 杭州,310058;
2. 浙江大学 浙江大学软弱土与环境土工教育部重点实验室,浙江 杭州,310058)
摘要:Green-Ampt入渗模型是以湿润锋至入渗面间的土体均达到饱和含水率为基础建立的,忽略非饱和区存在的实际情况,造成Green-Ampt模型计算结果不准确。针对这一情况,基于入渗分层假设,通过建立达西定律和雨水入渗质量守恒方程,推求入渗深度和时间的关系,并将其引入边坡安全系数分析。研究结果表明:入渗深度和时间的关系中,分层假设模型更贴近实测值,总体吻合性较高。同一深度,分层假设模型的入渗率始终高于Green-Ampt模型,但对于同一时刻,两模型入渗率相接近。同时,边坡安全系数中,以Green-Ampt模型计算的边坡安全系数过于保守,分层假设模型比Green-Ampt模型的边坡入渗深度和失稳时间有明显的延缓。正确分析土体内部入渗情况,将有助于准确预报边坡滑坡失稳,减小边坡加固,以免造成经济浪费。
关键词:分层假设;入渗;边坡;延缓
中图分类号:TU441 文献标志码:A 文章编号:1672-7207(2014)09-3211-08
Analysis slope safety based on infiltration model based on stratified assumption
ZHANG Jie1, 2, HAN Tongchun1, 2, DOU Hongqiang1, 2, MA Shiguo1, 2
(1. Research Center of Coastal and Urban Geotechnical Engineering, Zhejiang University, Hangzhou 310058, China;
2. Key Laboratory of Soft Soils and Geoenvironmental Engineering, Ministry of Education,
Zhejiang University, Hangzhou 310058, China)
Abstract: Green-Ampt infiltration model is set up based on saturation moisture content which is from wetting front to the infiltration surface, regardless of the unsaturated zone at actual situation, which makes Green-Ampt model calculation results inaccurate. In view of this situation, based on infiltration stratified hypothesis, ascertains the relationship between the infiltration depth and time was ascertained through establishing Darcy’s law and rainfall infiltration mass conservation equation, and was introduced into the slope safety factor analysis. The result shows that stratified hypothesis model is closer to the measured value and has a higher total anastomosis between the infiltration depth and time relationship. For same infiltration depth, stratified hypothesis model of infiltration rate is always higher than Green-Ampt model’s, but at the same infiltration time, two model infiltration rates are close. At the same time, the calculation of slope safety factor of the Green-Ampt model is too conservative, and the slope infiltration depth and instability time of stratified hypothesis model is obviously behind Green-Ampt model. The correct analysis of the internal soil infiltration will help us to accurately forecast the landslide slope instability, so as to reduce unnecessary slope reinforcement to cause economic waste.
Key words: stratified hypothesis; infiltration; slope; time delay
降雨入渗是指通过地表向下运动,补给土体水、地下水,是水分在土体中的一个动态分布过程[1],同时也是众多工程事故的主要诱发因素之一。在边坡工程中,由于降雨入渗的作用,边坡的稳定问题成为一个饱和-非饱和状态水的渗流和含水量变化引起非饱和土强度降低的复杂工程问题[2]。非饱和边坡降雨入渗过程中,入渗引起边坡地下水位线和边坡浅层含水率上升,造成孔隙水压力增大即基质吸力减小,因而边坡潜在危险滑动面抗剪强度不断减小,直到不能满足抗剪强度要求为止[3]。降雨导致边坡失稳已成为颇受国内外学者关注的问题,特别是随着非饱和土土力学的发展,已成为边坡工程的研究热点之一[4-8]。目前运用最广泛的Green-Ampt入渗模型基于湿润锋至入渗面间的土体达到完全饱和即含水率为饱和含水率,但众多试验研究表明:湿润锋至入渗面间的土体真实含水率并非理想的完全饱和状态。张华等[9]试验表明:湿润锋至入渗面间土体含水率只有饱和含水率的60%~80%左右,不可能达到完全饱和状态。毛丽丽等[10]对湿润锋至入渗面含水率进行了改进,提出含水率线性分布模式。Colaman和Bodman[11]最早基于干土积水条件下的垂直一维入渗试验,将含水率剖面分为4个区:饱和区、含水率有明显降落的过渡区、含水率变化不大的传导区和含水率迅速减小至初始值的湿润区。但上述研究是定性分析,并没有具体定量给出各部分大小,限制了其在入渗模型的应用。针对这一问题,本文作者基于彭振阳等[12]对入渗分层假设,并以此为基础推求了入渗深度和时间的关系,并将其引入边坡安全系数分析,发现分层假设模型计算的入渗率和边坡安全系数与Green-Ampt模型明显不同,Green-Ampt模型边坡失稳计算过于保守,极大可能造成不必要的经济损失,同时分层假定入渗模型内的参数可直接通过室内试验测得,有较大的实用性。
1 分层假定入渗模型
1.1 Green-Ampt入渗模型
1911年Green和Ampt[13]研究初始干燥土体在薄层积水时提出了一种入渗模型,在剖面上对其均匀的入渗过程进行概化与假定,其中最基本的假定是入渗过程中湿润锋面始终为一个干湿截然分开的界面,即湿润区为饱和含水率θs,湿润锋前为初始含水率θi,因此土壤水分剖面分布呈阶梯状,故该模型又称之为活塞模型,如图1所示。
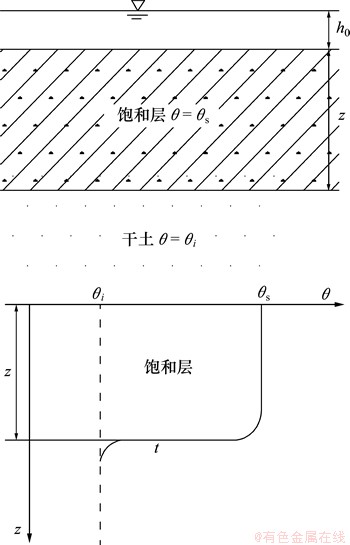
图1 Green-Ampt模型入渗图
Fig. 1 Green-Ampt model infiltration diagram
基于上述基本假设,根据质量守恒定律得到Green-Ampt入渗模型为:
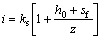 (1)
(1)
式中:i为入渗率;ks为饱和渗透系数;sf为湿润锋处平均基质吸力水头(角标“f”表示湿润峰处);z为概化湿润锋的深度;h0为地表处的积水水头。
Green-Ampt模型假设湿润锋至入渗面间的土体达到完全饱和,故累计入渗量为:
 (2)
(2)
式中:I为累积入渗量,θs和θi分别为饱和土体含水率和初始土体含水率。
根据累计入渗量和入渗率的导数关系,可得湿润峰深度随时间的函数关系z-t:
 (3)
(3)
该模型类似于Darcy定律,形式简单。然而该模型没有考虑非饱和区的影响,这会大大夸大入渗量,从而导致计算的入渗时间偏离实测值较大,在这种条件下该模型应用受到一定的限制。
1.2 分层假设模型
彭振阳等[12]基于Richards模拟了土体分层变化规律,提出入渗过程中将土体含水率分为以下3个部分,如图2所示:
饱和层
 ,0≤
,0≤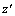 ≤
≤
过渡层
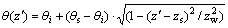 ,
, ≤
≤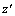 ≤z
≤z
干土层
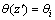 ,
,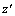 ≥z
≥z
其中:
 ;
; (4)
(4)
式中:zs为饱和层厚度;zw为过渡层厚度;z为湿润锋深度;ψ为过渡层占湿润层的比例。
随着入渗过程的推进,各层的深度和厚度都在不断变化。王文焰等[14]通过试验统计认为饱和层厚度约为湿润层厚度的一半。但彭振阳[12]通过模拟研究Richards入渗方程发现,随着入渗过程的推进,即湿润峰深度逐渐增加,过渡层占湿润层的比例不断减少,并且所占比例与湿润峰深度有很好的线性关系,如下式所示:
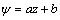 (5)
(5)
式中:a和b为系数。
基于上述分析,可对累计入渗量进行如下修正:
 (6)
(6)
前文所述,土体雨水入渗分3个部分,其中累计入渗量需要考虑的是饱和层和过渡层2个部分,故可以将其分开计算。对饱和层而言,其累积入渗量为:
 (7)
(7)
一般过渡层形态较为复杂,只能通过近似方式等效。王文焰等[15]采用椭圆形曲线反映过渡层内的含水率分布规律,其中拟合椭圆的水平半轴长度为饱和含水率与初始含水率之差,纵向半轴长度为过渡层厚度,其拟合结果与Richards方程计算值相关性很好,有很高的精度。因此作者同样也采用椭圆曲线反映过渡层内的含水率分布如图2所示,因而过渡层累积入渗量为1/4椭圆面积:
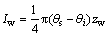 (8)
(8)
故总入渗量可表示为:

图2 分层假设模型入渗图
Fig. 2 Layered hypothesis model infiltration diagram
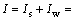
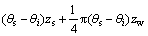 (9)
(9)
结合入渗分层假设,根据达西定律,Green-Ampt入渗率可修改为[15]:
 (10)
(10)
式(4)代入式(10)得:
 (11)
(11)
根据达西定律和入渗雨水质量守恒:
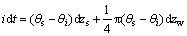 (12)
(12)
式(4)和(5)代入上式化简得:
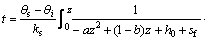
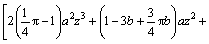
 (13)
(13)
积分求解得到:
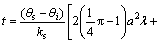
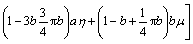 (14)
(14)
其中:
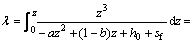

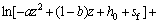
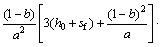
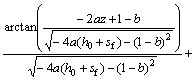



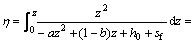
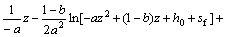
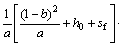
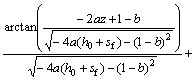
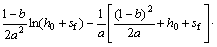

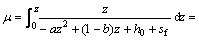
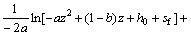



2 入渗分析与讨论
2.1 算例分析
为验证分层假设模型计算入渗时间的有效性。本算例采用彭振阳等[12]进行的室内一维入渗试验结果。该试验有机玻璃柱高度100 cm,内径20 cm,土柱高85 cm,积水水头为15 cm,其他具体土体参数如表1所示。
2.2 结果分析
图3所示为湿润峰实测值与模型计算值随时间变化曲线。从图3可知:分层模型与实测数据开始阶段很吻合,但入渗一定深度后,约在40 cm入渗深度,分层假设入渗时间计算值开始偏小于实测入渗时间。造成此原因有可能源于试验土样沿深部是不均质的,内部孔隙由细粒土颗粒填充,土质结构变密以及土体参数随深度发生变异性等,导致入渗速率变慢,入渗时间延缓。相比Green-Ampt模型计算值始终远高于实测值而言,分层假设模型计算值比Green-Ampt模型计算值更精确。因此雨水入渗时,有必要考虑非饱和区作用,分层假设模型更有利于准确预测入渗时间。
表1 土的基本参数
Table 1 Soil basic parameters


图3 湿润峰z-t变化曲线
Fig. 3 Wetting front depth-time curve
图4和图5所示为湿润锋处入渗率的变化曲线。从图4可知:入渗同一深度时,Green-Ampt模型的入渗率比分层假设模型偏低,且差值基本保持在0.02 cm/min左右。这主要是由于分层假设模型认为水头降低长度为zw并非z,且zw<z,这就相当于降低相同水头,分层假设的入渗路径变短。但从图5上分析,入渗同一时刻,Green-Ampt模型入渗率与分层假设模型开始阶段差别不大。这说明同一时刻分层假设引起的入渗率变化不是很明显,Green-Ampt可以很好反应某一时刻的入渗率。
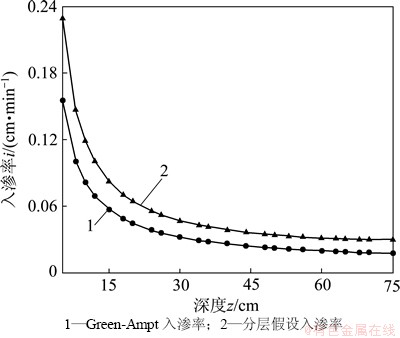
图4 入渗率i-z变化曲线
Fig. 4 Infiltration rate-depth curve

图5 入渗率i-t变化曲线
Fig. 5 Infiltration rate-time curve
3 非饱和土边坡稳定性分析
降雨入渗在边坡问题中十分常见,入渗是引起边坡失稳的重要因素,所以对边坡入渗问题分析十分重要。降雨入渗条件下,非饱和土边坡发生浅层破坏最为常见,且多为平行于边坡表面破坏[16-19],并可将其作为无限边坡来分析[21-22],其计算简图如图6所示。对于大面积无限长边坡,最危险面往往发生在湿润峰或潜在的积水面处[16, 19-20]。由于本文分层假设椭圆过渡区随着湿润锋深度增加不断减小,且过渡区所占面积较小,所以也将湿润锋处作为滑裂面。

图6 无限边坡入渗简图
Fig. 6 Infinite slope infiltration diagram
对边坡稳定分析作如下假设:1) 分析对象为一无限边坡;2) 湿润峰为一平行于坡面的近似平面;3)不计土条间水平作用力的影响。
从图6可知:湿润峰处安全系数可由湿润区总抗滑力与下滑力之比求解,湿润峰处抗滑力采用非饱和土的抗剪强度公式求解,下滑力即为湿润区土体的重度沿坡面的分量。即根据非饱和土摩尔库伦失效准则[23]和极限平衡法得到边坡稳定安全系数如下形式:
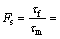
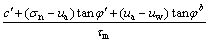 (15)
(15)
式中:τf为非饱和土抗剪强度;τm为一点的下滑力;γt为土的饱和重度;c′和j′分别为土的有效黏聚力和内摩擦角;jb为抗剪强度随基质吸力变化的吸力摩擦角;ua为孔隙压力,本文暂不考虑气体影响即为大气压力ua=0,(ua-uw)=-uw为土体湿润峰处的基质吸力γw-sf,γw为水的重度。
其中Green-Ampt模型中:
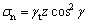 (16)
(16)
 (17)
(17)
根据分层假设模型椭圆过渡区可知:

 ≤
≤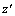 ≤
≤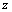 (18)
(18)
考虑非饱和区土体重度和含水率的联系,本文假设两者为线性关系,则过渡区不同位置的重度为:
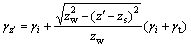 (19)
(19)
故分层假设模型中:
 (20)
(20)
 (21)
(21)
其中:式(1)、式(19)代入式(20)和式(21)即可求解。
Green-Ampt模型假定湿润区土体饱和,基质吸力为0,即式(22),分层假设则必须考虑基质吸力影响,即式(23),边坡在湿润峰处的安全系数分别为:
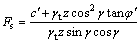 (22)
(22)
 (23)
(23)
为验证入渗过程中分层假设对边坡安全系数产生的影响,假设一无限长浅层边坡,边坡角度γ为30°(高宽比为1:1.73)如图6所示。渗流参数采用表1数据,稳定性参数如表2所示。
表2 土体计算参数
Table 2 Parameters of unsaturated soil

图7和图8所示分别为边坡安全系数随入渗深度z和入渗时间t的变化。可以看出:分层假设模型安全系数较Green-Ampt模型高,随着湿润锋快速下移,边坡安全系数快速下降,曲线显示入渗深度达到44 cm即时间为353 min时,Green-Ampt模型计算值认为边坡已经达到失稳状态,但此时分层假设边坡安全系数计算值认为边坡仍是安全的,并比Green-Ampt模型失稳深度和时间有较大延缓,Green-Ampt模型假设湿润锋至入渗面间的土体达到完全饱和会大大降低边坡安全系数,对边坡安全系数过于保守,有可能造成不必要的经济损失。

图7 边坡安全系数Fs-z的变化曲线
Fig. 7 Slope safety factor Fs-z curve
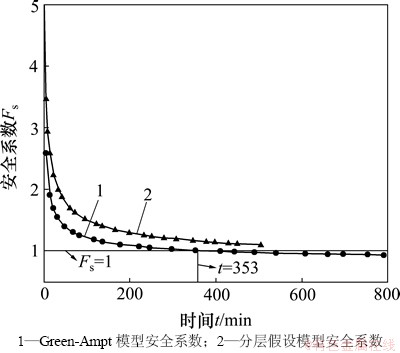
图8 边坡安全系数Fs-t的变化曲线
Fig. 8 Slope safety factor Fs-t curve
4 结论
1) 通过分层假设模型对比了传统Green-Ampt入渗模型,研究发现分层假设模型计算湿润锋深度比Green-Ampt模型更接近实测值,有更好的精确性。
2) 同一入渗深度,分层假设模型入渗率比Green-Ampt模型的值大,差值基本保持在0.02 cm/min左右。同一入渗时间,分层假设模型入渗率基本与Green-Ampt模型相持平,相差不大,Green-Ampt模型已能很好反映某一时刻的入渗率。
3) 随着湿润锋快速下移,边坡安全系数不断减小,研究发现,Green-Ampt模型边坡安全系数计算值比分层假设偏低,分层假设模型的失稳深度和时间有较大延缓。
参考文献:
[1] 刘汗, 雷廷武, 赵军. 土壤初始含水率和降雨强度对黏黄土入渗性能的影响[J]. 中国水土保持科学, 2009, 7(2): 1-6.
LIU Han, LEI Tingwu, ZHAO Jun. Effects of initial soil water content and rainfall intensity on loess infiltration capacity[J]. Science of Soil and Water Conservation, 2009, 7(2): 1-6.
[2] 张芳枝, 梁志松, 周秋娟. 非饱和土性状及其边坡稳定性[M]. 北京: 中国水利水电出版社, 2011.
ZHANG Fangzhi, LIANG Zhisong, ZHOU Qiujuan. Traits and slope stability of unsaturated soil[M]. Beijing: China WaterPower Press, 2011.
[3] 周家文, 徐卫亚, 邓俊晔, 等. 降雨入渗条件下边坡的稳定性分析[J]. 水利学报, 2008, 39(9): 1066-1073.
ZHOU Jiawen, XU Weiya, DENG Junye, et al. Stability analysis of slope under the condition of rainfall infiltration[J]. Journal of Hydraulic Engineering, 2008, 39(9): 1066-1073.
[4] 许建聪, 尚岳全. 降雨作用下碎石土滑坡解体变形破坏机制研究[J]. 岩土力学, 2008, 29(1): 109-113.
XU Jiancong, SHANG Yuequan. Study on mechanism of disintegration deformation and failure of debris landslide under rainfall[J]. Rock and Soil Mechanics, 2008, 29(1): 109-113.
[5] CAI F, UGAI K. Numerical analysis of rainfall effects on slope stability[J]. International Journal of Geomechanics, 2004, 4(2): 69-78.
[6] Kima J, Jeong S, Park S, et al. Influence of rainfall-induced wetting on the stability of slopes in weathered soils[J]. Engineering Geology, 2004, 75(3/4): 251-262.
[7] Zhan T L T, Ng C W W. Analytical analysis of rainfall infiltration mechanism in unsaturated soils[J]. International Journal of Geomechanics, 2004, 4(4): 273-284.
[8] 李兆平, 张弥. 考虑降雨入渗影响的非饱和土边坡瞬态安全系数研究[J]. 土木工程学报, 2001, 34(5): 57-61.
LI Zhaoping, ZHANG Mi. Effects of rain infiltration on transient safety of unsaturated soil slope[J]. China Civil Engineering Journal, 2001, 34(5): 57-61.
[9] 张华, 吴争光. 封闭气泡对一维积水入渗影响的试验研究[J]. 岩土力学, 2009, 30(2): 132-137.
ZHANG Hua, WU Zhengguang. Experimental research on the effect of entrapped air on one-dimensional ponded water infiltration[J]. Rock and Soil Mechanics, 2009, 30(2): 132-137.
[10] 毛丽丽, 雷廷武. 用修正的Green-Ampt模型确定土壤入渗性能的速算方法[J]. 农业工程学报, 2010, 26(12): 53-57.
MAO Lili, LEI Tingwu. Fast method for estimating soil infiltrability with modified Green-Ampt model[J]. Transactions of the Chinese Society of Agricultural Engineering, 2010, 26(12): 53-57.
[11] Bodman G B, Coleman E A. Moisture and energy conditions during downward entry of water into soils[C]// Soil Science Society of America Proceedings. 1943: 116-122.
[12] 彭振阳, 黄介生, 伍靖伟, 等. 基于分层假设的Green-Ampt模型改进[J]. 水科学进展, 2012, 23(1): 59-66.
PENG Zhenyang, HUANG Jiesheng, WU Jingwei, et al. Modification of Green-Ampt model based on the stratification hypothesis[J]. Advance in Water Science, 2012, 23(1): 59-66.
[13] Green W H, Ampt G A . Studies on soil physics: 1. Flow of air and water through soils[J]. Journal of Agricultural Science, 1911, 4(1): 1-24 .
[14] 王文焰, 王全九, 张建丰, 等. 甘肃秦王川地区土壤水分运动参数及相关性[J]. 水土保持学报, 2002, 41(1): 110-113.
WANG Wenyan, WANG Quanjiu, ZHANG Jianfeng, et al. Soil hydraulic properties and correlation in Qingwangchuan area of Gansu Province[J]. Science of Soil and Water Conservation, 2002, 41(1): 110-113.
[15] 王文焰, 汪志荣, 王全九, 等. 黄土中Green-Ampt入渗模型的改进与验证[J]. 水利学报, 2003, 35(1): 30-35.
WANG Wenyan, WANG Zhirong, WANG Quanjiu, et al. Improvement and evaluation of the Green-Ampt model in loess soil[J]. Journal of Hydraulic Engineering, 2003, 35(1): 30-35.
[16] Rahardjo H, Lim T T, Chang M F, et al. Shear-strength characteristics of a residual soil[J]. Canadian Geotechnical Journal, 1994, 32(1): 60-77.
[17] Sung E C. Infiltration analysis to evaluate the surficial stability of two-layered slopes considering rainfall characteristics[J]. Engineering Geology, 2009, 105(1/2): 32-43.
[18] Fourie A B, Rowe D, Blight G E. The effect of infiltration on the stability of the slopes of a dry ash dump[J]. Geotechnique, 1999, 49(1): 1-13.
[19] 王智磊, 孙红月, 尚岳全. 基于地下水位变化的滑坡预测时序分析[J]. 岩石力学与工程学报, 2011, 30(11): 2276-2284.
WANG Zhilei, SUN Hongyue, SHANG Yuequan. Time series analysis of landside prediction based on groundwater level variation[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(11): 2276-2284.
[20] Kenneth G, Xue J. A simple method to analyze infiltration into unsaturated soil slopes[J]. Computers and Geotechnics, 2008, 35(2): 223-230.
[21] Cho S, Lee S. Evaluation of surficial stability for homogeneous slopes consideration rainfall characteristics[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2002, 128(9): 756-763.
[22] Rahardjo H, Lim T T, Chang M F, et al. Shear-strength characteristics of a residual soil[J]. Canadian Geotechnical Journal, 1995, 32(1): 60-77.
[23] Fredlund D G, Morgenstern N R, Widger N R. The shear strength of unsaturated soil[J]. Canadian Geotechnical Journal, 1978, 15(3): 313-321.
(编辑 陈爱华)
收稿日期:2013-11-13;修回日期:2014-03-08
基金项目:国家自然科学基金资助项目(51178423)
通信作者:韩同春(1969-),男,河南卫辉人,副教授,博士,从事边坡稳定方面的研究;电话:0571-88208780;E-mail: htc@zju.edu.cn