ARTICLE

J. Cent. South Univ. (2019) 26: 2136-2148

DOI: https://doi.org/10.1007/s11771-019-4161-0

Hybrid LEAP modeling method for long-term energy demand forecasting of regions with limited statistical data

CHEN Rui(陈睿), RAO Zheng-hua(饶政华), LIAO Sheng-ming(廖胜明)

School of Energy Science and Engineering, Central South University, Changsha 410083, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019

Abstract: An accurate long-term energy demand forecasting is essential for energy planning and policy making. However, due to the immature energy data collecting and statistical methods, the available data are usually limited in many regions. In this paper, on the basis of comprehensive literature review, we proposed a hybrid model based on the long-range alternative energy planning (LEAP) model to improve the accuracy of energy demand forecasting in these regions. By taking Hunan province, China as a typical case, the proposed hybrid model was applied to estimating the possible future energy demand and energy-saving potentials in different sectors. The structure of LEAP model was estimated by Sankey energy flow, and Leslie matrix and autoregressive integrated moving average (ARIMA) models were used to predict the population, industrial structure and transportation turnover, respectively. Monte-Carlo method was employed to evaluate the uncertainty of forecasted results. The results showed that the hybrid model combined with scenario analysis provided a relatively accurate forecast for the long-term energy demand in regions with limited statistical data, and the average standard error of probabilistic distribution in 2030 energy demand was as low as 0.15. The prediction results could provide supportive references to identify energy-saving potentials and energy development pathways.

Key words: energy demand forecasting with limited data; hybrid LEAP model；ARIMA model；Leslie matrix; Monte-Carlo method

Cite this article as: CHEN Rui, RAO Zheng-hua, LIAO Sheng-ming. Hybrid LEAP modeling method for long-term energy demand forecasting of regions with limited statistical data [J]. Journal of Central South University, 2019, 26(8): 2136-2148. DOI: https://doi.org/10.1007/s11771-019-4161-0.

1 Introduction

With the rapid economic growth and large- scale industrialization, China’s energy consumption and greenhouse gas (GHG) emission have significantly increased [1-3]. A series of laws and decrees have been taken into effects with the attempt to control energy consumption and improve energy efficiency [4-6]. However, it is inevitable that China requires more energy supply to sustain positive growth in population and economy, improve industrialization and living standards in coming decades. It is always urgent to formulate appropriate energy development strategies due to the challenges in energy shortage and supply security. A reliable long-term energy demand forecasting is necessary to identify future energy demand and provide effective supports for drafting policy decisions. However, the future development of Chinese energy system may not follow the same trajectory as that in the past due to the undergoing reform in economy and energy [7]. Therefore, choosing appropriate modeling methods according to characteristics of forecasted areas is the first task for accurate energy demand forecast.

Developing forecasting models is also determined by the availability of relevant data. The structural economic change and increasing share of rural households lead to some indirect effects on future energy demand [8]. Compared with population and economy, energy consumption database in many sectors is structurally deficient or limited, leading to insufficient historical data to build scenarios and models. When the collected data are downscaling for the calculation adjustments from nation-level to the regional and city levels, the uncertainty in calculated data may increase [9].

In the past decades, different methods from statistical to machine learning have been applied for energy demand forecast of China. YUAN et al [10] used autoregressive integrated moving average (ARIMA) model and gray model (GM) to forecast the primary energy demand of China. The sensitivities of these two models to fluctuations in historical data were compared. WANG et al [11] compared the accuracy of single, hybrid and non-linear time series techniques used in China energy demand forecast. YU et al [12] developed a hybrid particle swarm optimization (PSO) and genetic algorithm (GA) model to forecast the energy demand of China during 2010 to 2020. However, considering the lack of historic time-series data, LEAP model may be a better option for its low initial data requirements and flexible structure [13]. It is also a suitable modeling platform for in-depth regional analysis. HUANG et al [14] employed LEAP model to predict the long-term energy supply and demand in Taiwan, China. LIN et al [15] developed a detailed LEAP model to analyze the future trends of energy demand and GHG emissions in a city.

Although many efforts have been made in modeling methods of energy demand forecasting, it is still a big challenge to accurately predict the energy demand in regions with limited statistical data, as discussed in Section 2. Previous studies either used simple statistical models with limited accuracy or developed AI-based approaches with complex model structure. For these regions, it is necessary to develop appropriate forecasting methods according to the available data in different economic sectors.

In this study, a hybrid model has been proposed by integrating LEAP, AMRIMA, Leslie matrix and Monte-Carlo method for the long-term energy demand forecasting in regions with limited statistic data. According to the relatively rich time-series data on population and economy, Leslie matrix and ARIMA are separately developed to predict the future population, industrial structure and transportation turnover. Monte-Carlo method is used to provide the probabilistic distributions of forecasted energy demand, for evaluating the suitability of hybrid model developing and parameters setting. By taking Hunan province of China as a typical case, the hybrid modeling method is demonstrated to forecast the energy demand in different scenarios from 2013 to 2030. The uncertainty of forecasted energy demand in business-as-usual scenario is evaluated, and the effects of energy policies on energy demand and intensity are analyzed by comparing forecasting results under different scenarios.

2 Literature review

In terms of the underling methodology, the modeling methods used in energy demand forecasting can be classified into [16]:

1)Statistical models, including regression-based model and time series methods such as ARIMA and GM;

2)Artificial intelligence (AI) based approaches, including artificial neural network (ANN), support vector regression (SVR), fuzzy logic, GP, PSO, ant colony optimization (ACO) and artificial bee colony (ABC);

3)Bottom-up models, such as Market allocation (MARKAL) and LEAP model.

Table 1 compares the models commonly used for energy demand forecasting. Statistical models are flexible and relatively easy to develop; thus, it is more common than computational intelligence and mathematical programming methods. For instance, ARIMA is one of the most popular models used in stationary time series with no missing sample [19]. GM is practical in characterizing unknown systems with incomplete information in time series. It can extract hidden information from incomplete and discrete data [44]. However, these models could not accurately capture the characteristics of energy demand in regions with limited data [8]. The pre-assumed linear form of ARIMA model limits the result accuracy with limited data, and GM is not suitable for long-term forecasting because growth trends in different periods cannot be reflected in the modeling of unknown systems.

Table 1 Summary of most frequent models and techniques used in energy demand forecasting

Continued

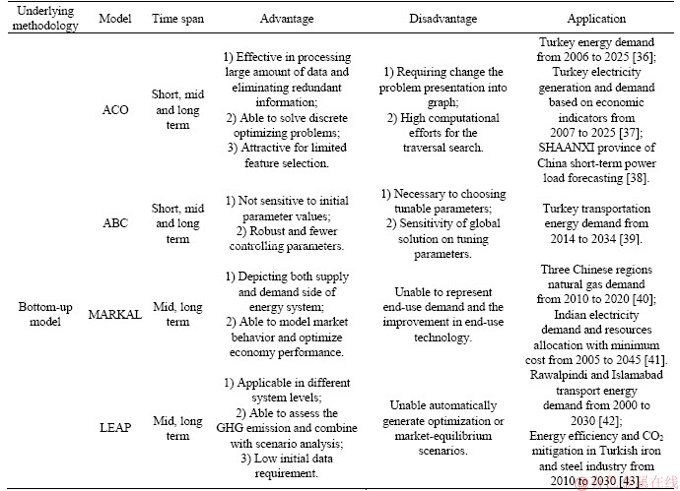
Compared with statistics methods, AI-based approaches ensure satisfactory accuracy and are more suitable for solving the nonlinear, discontinuous and unknown variable relationships involved in long-term forecasting. Furthermore, researchers have also proposed hybrid AI-based models to improve the forecasting accuracy and solve the nonlinearity in long-term forecasting [45-48]. However, these methods still suffer the shortcoming of black-box problem and cannot generate certain prediction equations based on input data [49]. Too many control parameters are required and the results are quite sensitive to initial parameter values [6]. Meanwhile, these methods are computationally intensive, slow in operation, complex in model structure and complicated in control parameter adjustment [50].

In terms of proper accuracy and applicability, LEAP model may be more suitable for the long-term modeling of energy systems with limited data. Compared with statistical models, LEAP model can produce more realistic projections with detailed sectorial representations; compared with AI-based models, LEAP has flexible model structure and relatively low requirements of initial data; and compared with MARKAL model, LEAP models technologies explicitly and is independent of market behavior and production frontiers [7].

Nowadays, LEAP model has been widely applied to energy demand forecasting in sectorial [51], municipal [15, 52], national [53], regional [54], and global scales [5]. To improve the estimation accuracy, some researchers have integrated some other technologies into LEAP model. SADRI et al [55] employed GM and ANN methods to predict the key input data in LEAP model, i.e., the activity levels and energy intensities of light duty vehicle. NOJEDEHI et al [56] developed a hybrid model with LEAP and IPCC (intergovernmental panel on climate change) model to estimate the effects of sustainable wasting management in Tehran energy demand and GHG emissions. KALE et al [57] forecasted the electricity supply and demand scenarios by LEAP and used ARIMA model to find the growth rates of sector economy. However, these studies paid a lot attention to economy development, and had less effort in population.

Although many efforts related to LEAP model have been dedicated, few of them involves the uncertain information in model structure and input parameters. Most previous studies simplified the associated parameters such as activity level and energy intensity as deterministic values, and thus failed to provide probabilistic distributions of future energy demand. Some researchers have used Monte-Carlo method to evaluate the uncertainty of bottom-up models and forecasted results [58-60]. The uncertainties in single or hybrid LEAP model and their forecasted results are still unclear. Therefore, it is necessary to promote a suitable modeling method based on LEAP to solve the limitation of required data and evaluate effects of data uncertainty on the predicted energy demand.

3 Hybrid LEAP modeling method for energy demand forecasting

Figure 1 shows the flowchart of hybrid modeling method for long-term energy demand forecasting in regions with limited data proposed in this study. Based on the LEAP model, several modeling methods are integrated as follows:

1) The energy flow Sankey diagram is used to identify the structure and amount of statistic data, and becomes reference to determine the LEAP model structure.

2) Considering the characteristics of historical data, ARIMA method, Leslie matrix and average annual growth rate (AGR) are used to predict the variations of input parameters. For the linearity of time series data in industrial structure and transportation turnover, ARIMA models are used to forecast the industrial structure and turnover; Leslie matrix is developed to forecast future population; and AGR method is used to determine the variations in GDP and energy intensity.

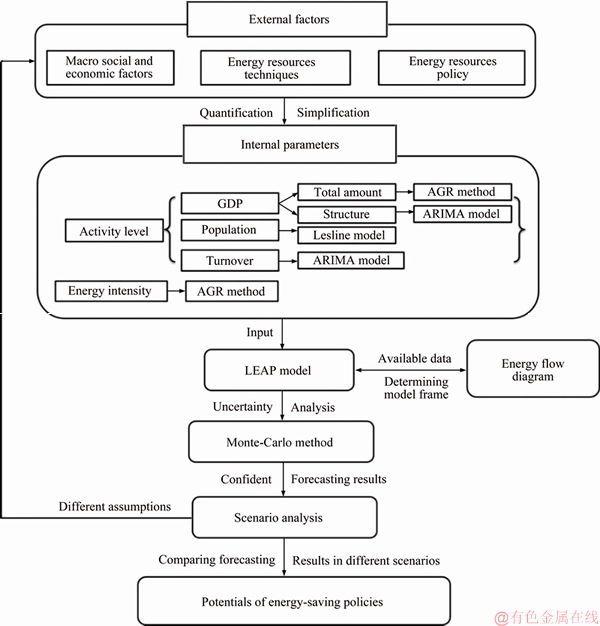
Figure 1 Flowchart of proposed hybrid modeling method

3) After forecasting key input parameters under the assumption in corresponding scenarios, the energy demand during forecasting horizon can be determined by LEAP model.

4) The probabilistic distribution of forecasted energy demand can be obtained by Monte-Carlo method, and thus the uncertainty of hybrid model and forecasted results can be assessed.

3.1 LEAP model

LEAP model is an end-use driven analysis platform and its model structure can be suitably determined by the available data. The framework can be disaggregated into a hierarchical tree structure of four levels: sector, sub-sector, end-use, and device [59]. The energy demand in each sector is equal to the product of activity level and energy intensity. The total energy demand is the sum of energy demand in each sector, which can be presented as [13]:

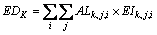                  (1)

where ED is the total energy demand; AL is the activity level; EI is the energy intensity; i and j respectively refer to the types of sector and device/vehicle; k is the fuel type. The energy demand is calculated in the unit of ton of standard coal equivalent (tce, i. e., 1 tce=29.31 GJ) and the conversion coefficients for different fuels are extracted from Ref. [61].

After developing suitable LEAP model according to the energy flow diagram in Sankey, scenario analysis is often combined with LEAP model to track future energy developing pathways under any particular set of conditions [62]. Based on scenario analysis, the impacts of implement policies and interactions among multiple pathways can be briefly assessed in forecasting horizons.

3.2 Leslie matrix

Leslie matrix is a professional population prediction model. The input parameters for the model mainly include the current population, mortality by age and sex, and fertility rate of women at childbearing ages. The main modeling steps include establishing a life table, constructing a survival transition matrix, establishing a birth model and forecasting the total population [63].

3.3 ARIMA model

ARIMA models are generic models and just use stationary time series data to express the reaction of variables with stochastic variation. Based on historical data, ARIMA can be performed by four steps: 1) time series data preprocess, 2) model identification and parameters estimation, 3) model recognition, and 4) model verification and forecasting [19, 45].

The ARIMA (p,q) model refers to the model with p autoregressive terms and q moving-average terms, which can be written as:

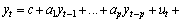
                      (2)

where c is a constant; a₁,…,a_p are the parameters of AR(p); random variable u_t is white noise of AR(p); m₁,…m_q are the parameters of MA(q); u is the expectation of y_t; u_t, u_t-1,…, and u_t-q are white noise error terms of MA(q).

3.4 Method for uncertainty analysis

Monte-Carlo method is one of the most effective methods widely used in addressing energy demand forecasting problems with uncertain inputs changing over time [64]. Monte-Carlo can provide probabilistic solution sets by generating random scenarios from defined continuous distributions. Figure 2 shows the framework of Monte-Carlo method used in this study. To perform this assessment, each input parameter in LEAP model is described as being drawn from a statistical distribution, and the functional relations between input variables and energy demand are generated from the LEAP framework.

4 Results and discussion

In this paper, Hunan province, China was taken as a typical case to apply the proposed hybrid model described in Section 3. The relevant data were found in statistic yearbooks [65-67], census [68, 69], and reports [70, 71]. Based on the available data, the year of 2012 was applied as the base year. The input parameters, including the variations of activity levels and energy intensities, are estimated by the corresponding methods according to the scenario analysis.

Figure 2 Framework of Monte-Carlo method

4.1 Energy flow and LEAP modeling framework

Figure 3 shows the energy flow of Hunan Province, China in 2012 by Sankey diagram [72]. In this figure, the entire energy flow process is divided into three parts that are energy production, energy conversion and final energy consumption, and the width of line corresponds to the quantity of energy flow. On the left side of Figure 3, the local energy production and energy import, including the primary energy and electricity, are presented in terms of the amount of each energy type. In the middle part, the transportation and conversion of each energy type are tracked by corresponding energy flow. On the right side, the final distribution and utilization of each energy type are separated into various sectors. It is clear that the coal was the main energy in total energy consumption, and the industry was the largest energy user followed by service and others and residential sector.

According to available energy data shown in Figure 3, the energy demand sectors are classified into primary industry (including agriculture, forestry, animal husbandry and fishery), industry, construction, transportation, service and others, and residential sector. Therefore, the energy demand of Hunan, China is divided into these six sectors in LEAP model. For detailed analysis, the industry sector is divided into two subsectors, i.e., high energy-consuming industries and other industries. This helps to identify the detail energy-saving potential in industry sector, especially for high energy-consuming industries, which accounts for almost 50% of total industry energy consumption in 2012 [66]. Furthermore, the transportation sector consists of passenger and freight transportation subsectors. For passenger and freight transportation subsectors, AL refers to the turnover and EI refers to the energy consumption of per unit of turnover.

4.2 Scenarios analysis

By taking the year of 2012 as the base year, three scenarios are proposed to quantitatively determine the energy demand from 2013 to 2030 and identify energy-saving potentials under different development pathways.

1) Business as usual (BAU) Scenario. This scenario demonstrates that current practices in Hunan province would continue in the absence of more incentive policies. The economy, population, energy production and consumption would naturally develop based on current patterns and historical trends. GDP is predicted by annual growth rate method and the population is estimated using the Leslie population matrix model. Based on historical data from 1980 to 2011, the industrial structure and transportation turnover are estimated by ARIMA model, respectively. Furthermore, the energy intensity in each sector is determined by the average growth rate from 2005 to 2012. Table 2 shows the detailed assumptions of parameters.

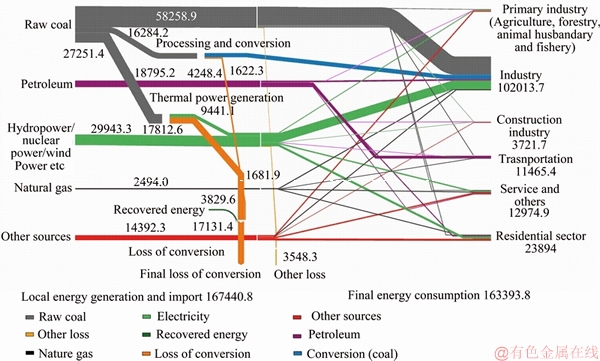
Figure 3 Energy flow diagram of Hunan province in 2012 (unit: 10³ tce)

Table 2 Key assumptions in BAU, AGC and IES scenarios

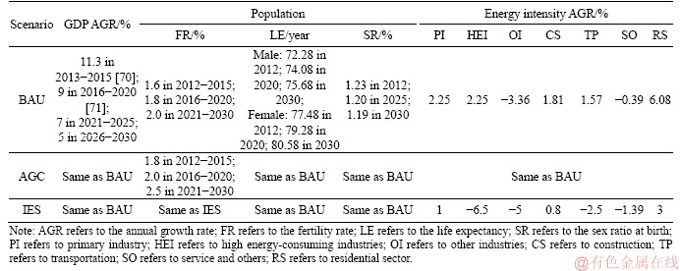
2) Active government control (AGC) scenario. This scenario demonstrates that the government would implement incentive administrational economy policies and second-child policy to adjust the industrial structure and increase the population. The macro-control policies include eliminating backward production capacity and developing high-tech and energy-efficient industry. The growth rates for the first, second and third industries, are, respectively, assumed as 2.5%, 9.0% and 10.7%, and other assumptions are the same as BAU.

3) Incentive energy-saving (IES) scenario. This scenario demonstrates that on the basis of AGC, a variety of incentive energy-saving measures, such as energy performance contract, energy efficiency standards and labeling program, market-oriented energy price and carbon (energy- savings) trading schemes, would be employed. With these policies, the energy efficiency in some sectors, such as high energy-consuming industries and residential sector, would significantly increase, while other assumptions are the same as AGC.

4.3 Energy demand forecasting in different scenarios

Figure 4 shows the total amount of energy demand and corresponding energy intensity under different scenarios in forecasting horizon. For all the scenarios, the energy demands gradually increase and the corresponding energy intensities (i.e., the ratio of energy demand and GDP) decrease by year. From 2014 to 2026, the energy demand and energy intensity in AGC are slightly less than those in BAU due to the adjustment of industrial structure. After 2026, the energy demand and energy intensity in AGC become slightly greater than those in BAU because of the population growth. For the energy demand and energy intensity in IES, significant reductions are observed due to the implement of advanced energy saving policies.

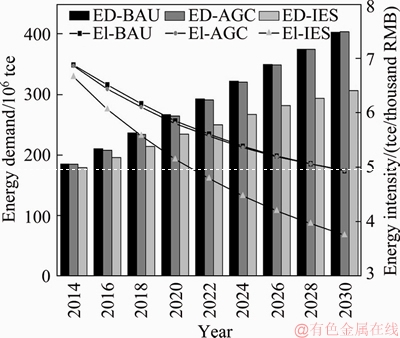
Figure 4 Energy demand and energy intensity under three scenarios from 2014 to 2030

To further identify the energy-saving potential in each sector, Figure 5 shows the energy demand savings in six sectors under AGC and IES scenarios with reference to BAU. For AGC scenario, energy demand savings in industry sector can be observed due to the reduced proportion of industry in GDP. But after 2026, the energy demand increases in service and others sector and residential sector are almost equal or even larger than the energy demand reduction in industry sector. This is also the reason that the energy demand in AGC is higher than that in BAU after 2026, as shown in Figure 5. For IES scenario, the energy demand saving in each sector increases by year, and the industry sector contributes the largest energy demand saving, followed by residential and service and others sectors. The results indicate that the energy-saving policies play a greater role than the regulation of industry structure, and the positive effect will increase with time.

Figure 6 shows the sector structure of energy demand in typical years under three scenarios. Obviously, in each scenario, industry occupies the largest energy demand, but its proportion decreases over time. In contrast, the proportion of energy demand in residential sector increases over time, as well as the service and others sector. In IES scenario, residential sector accounts for a lower proportion of energy demand than in BAU and AGC scenario, while the service and others sector accounts for a higher proportion. The results indicate that incentive energy saving policies are beneficial to transform and upgrade the structure of energy demand.

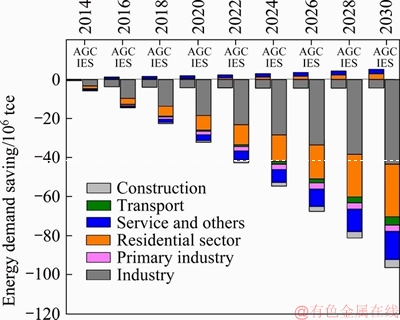
Figure 5 Comparison of sector energy demand of AGC and IES with reference to BAU

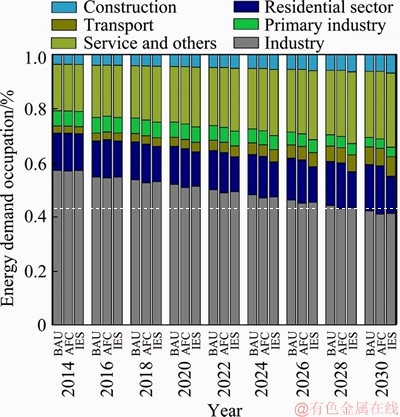
Figure 6 Energy demand structure under different scenarios from 2014 to 2030

4.4 Uncertainty analysis

Figure 7 shows the frequency distributions of forecasted energy demand in typical years under BAU scenario. The probability distributions of the activity levels and energy intensities in different sectors are determined according to their estimation methods. As shown, the frequency distribution of forecasted energy demand approximately follows a gamma distribution in 2014, a Weibull distribution in 2018, a logic distribution in 2022, Weibull distributions in 2026 and 2030, with average standard errors of 0.03, 0.06, 0.10, 0.14, and 0.15, respectively. Although the average standard errors of these energy demand distributions increase with time, the difference between the maximum and middle energy consumption in each year is less than 40 million tce as shown in Figure 7. Meanwhile, the expectations of these energy demand distributions are very close to the forecasted results in LEAP. Though the uncertainty of forecasted energy demand increases with time, the prediction results are credible in terms of the orders of magnitude. Therefore, the proposed hybrid method can contribute to a reasonable long-term energy demand forecast for regions with limited statistical data.

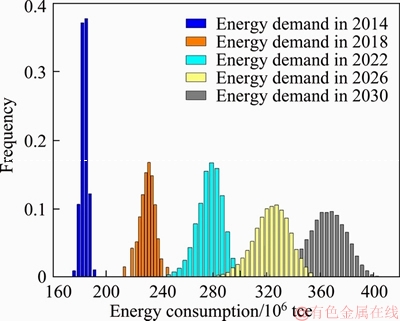
Figure 7 Probabilistic distributions of predicted energy demand under BAU scenario

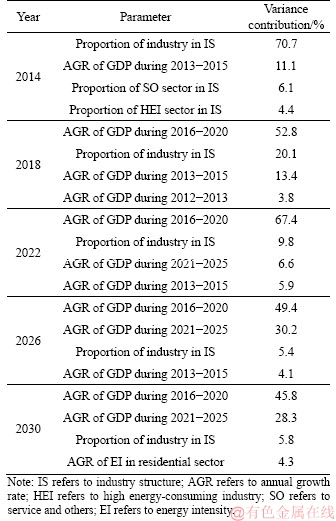
Table 3 shows the most sensitive parameters to the uncertainty of forecasted energy demand in different years under BAU scenario. It is clear that the annual growth rates of GDP contribute to the largest variance of energy demand, followed by the proportion of key sectors in industry structure. This is because energy demand strongly depends on GDP, while the industry structure determines the GDP in each sector. Meanwhile, the annual variation of GDP is estimated by experts assuming, which follows the minimum extreme distribution. The difference between the minimum extreme value and expectation is relatively large.

Table 3 Most sensitive parameters to uncertainty of predicted energy demand under BAU scenario

5 Conclusions

In this paper, a hybrid modeling method based on LEAP model has been proposed to predict the long-term energy demand in regions with limited statistical data. Leslie matrix, ARIMA model, scenario analysis and Monte-Carlo method are combined with LEAP model to enable accurate forecasting and assess the energy-saving potential of drafting policies. To estimate the applicability of proposed hybrid model, Hunan province, China was taken as a typical case and its energy demand under three scenarios from 2013 to 2030 was forecasted.

The results showed that, by taking detailed energy situation analysis in Sankey energy flow diagram, the LEAP model structure was flexibly and appropriately determined according to the data availability. The utilization of Leslie matrix and ARIMA model quantitatively provided accurate variations of key parameters, including population, GDP, industrial structure and transportation turnover. Based on the Monte-Carlo method, the probabilistic distributions of energy demand in forecasting horizon were provided and the uncertainty of energy demand in BAU scenario was identified. Although the average standard errors of energy demand distributions increased over time, the forecasted energy demand in 2030 was still reliable in terms of magnitude. Furthermore, the proposed hybrid modeling method could be easily developed in other regions.

References

[1] LI Y, TANG W, CHEN Y, LIU J. Potential of acetone-butanol-ethanol (ABE) as a biofuel [J]. Fuel, 2019, 242: 673-686. DOI: 10.1002/j.fuel.2019.01.063.

[2] CHEN R, RAO Z, LIAO S M. Determination of key parameters for sizing the heliostat field and thermal energy storage in solar tower power plants [J]. Energy Conversion and Management, 2018, 177: 385-394. DOI: 10.1016/ j.enconman.2018.09.065.

[3] LI Sai-wei, SUN Zhi-qiang, XU Bing, YANG Hong. Melting of phase change material from an isothermal vertical wall in a semi-enclosure [J]. International Journal of Heat and Mass Transfer, 2018, 127: 1041-1052. DOI: 10.1016/ j.ijheatmasstransfer.2018.08.101.

[4] MA Wei-wu, XUE Xin-pei, LIU Gang. Techno-economic evaluation for hybrid renewable energy system: Application and merits [J]. Energy, 2018, 159: 385-409. DOI: 10.1016/ j.energy.2018.06.101.

[5] LIU G, LI M, ZHOU B, CHEN Y, LIAO S. General indicator for techno-economic assessment of renewable energy resources [J]. Energy Conversion and Management, 2018, 156: 416- 426. DOI: 10.1016/j.enconman.2017.11.054.

[6] SONG Y, ZHU X, SUN Z, TANG D. Experimental investigation of particle-induced pressure loss in solid–liquid lifting pipe [J]. Journal of Central South University, 2017, 24(9): 2114-2120. DOI: 10.1007/s11771-017-3620-8.

[7] BHATTACHARYYA S C, TIMILSINA G R. Modelling energy demand of developing countries: Are the specific features adequately captured? [J]. Energy Policy, 2010, 38(4): 1979-1990. DOI: 10.1016/j.enpol.2009.11.079.

[8] URBAN F, BENDERS R M J, MOLL H C. Modelling energy systems for developing countries [J]. Energy Policy, 2007, 35(6): 3473-3482. DOI: 10.1016/j.enpol.2006.12.025.

[9] KEIRSTEAD J, JENNINGS M, SIVAKUMAR A. A review of urban energy system models: Approaches, challenges and opportunities [J]. Renewable and Sustainable Energy Reviews, 2012, 16(6): 3847-3866. DOI: 10.1016/j.rser.2012. 02.047.

[10] YUAN C, LIU S, FANG Z. Comparison of China′s primary energy consumption forecasting by using ARIMA (the autoregressive integrated moving average) model and GM (1, 1) model [J]. Energy, 2016, 100: 384-390. DOI: 10.1016/j.energy.2016.02.001.

[11] WANG Q, LI S, LI R. Forecasting energy demand in China and India: Using single-linear, hybrid-linear, and non-linear time series forecast techniques [J]. Energy, 2018, 161: 821-831. DOI: 10.1016/j.energy.2018.07.168.

[12] YU S, ZHU K, ZHANG X. Energy demand projection of China using a path-coefficient analysis and PSO–GA approach [J]. Energy Conversion and Management, 2012, 53(1): 142-153. DOI: 10.1016/j.enconman.2011.08.015.

[13] SEI. Long-range energy alternatives planning system: user guide: for LEAP version 2008 [M]. Boston: Stockholm Environment Institute (SEI), 2010.

[14] HUANG Y, BOR Y J, PENG C Y. The long-term forecast of Taiwan’s energy supply and demand: LEAP model application [J]. Energy Policy, 2011, 39(11): 6790-6803. DOI: 10.1016/j.enpol.2010.10.023.

[15] LIN J, CAO B, CUI S, WANG N, BAI X. Evaluating the effectiveness of urban energy conservation and GHG mitigation measures: The case of Xiamen city, China [J]. Energy Policy, 2010, 38(9): 5123-5132. DOI: 10.1016/ j.enpol.2010.04.042.

[16] SUGANTHI L, SAMUEL A A. Energy models for demand forecasting—A review [J]. Renewable and Sustainable Energy Reviews, 2012, 16(2): 1223-1240. DOI: 10.1016/ j.rser.2011.08.014.

[17] BILGILI M, SAHIN B, YASAR A, SIMSEK E. Electric energy demands of Turkey in residential and industrial sectors [J]. Renewable and Sustainable Energy Reviews, 2012, 16(1): 404-414. DOI: 10.1016/j.rser.2011.08.005.

[18] SEN P, ROY M, PAL P. Application of ARIMA for forecasting energy consumption and GHG emission: A case study of an Indian pig iron manufacturing organization [J]. Energy, 2016, 116: 1031-1038. DOI: 10.1016/j.energy.2016. 10.068.

[19] OLIVEIRA E M D, OLIVEIRA F L C. Forecasting mid-long term electric energy consumption through bagging ARIMA and exponential smoothing methods [J]. Energy, 2018, 144: 776-788. DOI: 10.1016/j.energy.2017.12.049.

[20] XU N, DING S, GONG Y, BAI J. Forecasting Chinese greenhouse gas emissions from energy consumption using a novel grey rolling model [J]. Energy, 2019, 175: 218-227. DOI: 10.1016/j.energy.2019.03.056.

[21] XIONG P P, DANG Y G, YAO T X, WANG Z. Optimal modeling and forecasting of the energy consumption and production in China [J]. Energy, 2014, 77: 623-634. DOI: 10.1016/j.energy. 2014.09.056.

[22] MOLLAIY-BERNETI S. Developing energy forecasting model using hybrid artificial intelligence method [J]. Journal of Central South University, 2015, 22(8): 3026-3032. DOI: 10.1007/s11771-015-2839-5.

[23] EKONOMOU L. Greek long-term energy consumption prediction using artificial neural networks [J]. Energy, 2010, 35(2): 512-517. DOI: 10.1016/j.energy.2009.10.018.

[24] ARDAKANI F J, ARDEHALI M M. Long-term electrical energy consumption forecasting for developing and developed economies based on different optimized models and historical data types [J]. Energy, 2014, 65: 452-461. DOI: 10.1016/j.energy.2013.12.031.

[25] SON H, KIM C. Short-term forecasting of electricity demand for the residential sector using weather and social variables [J]. Resources, Conservation and Recycling, 2017, 123: 200-207. DOI: 10.1016/j.energy.2019.03.056.

[26] HONG W C. Electric load forecasting by seasonal recurrent SVR (support vector regression) with chaotic artificial bee colony algorithm [J]. Energy, 2011, 36(9): 5568-5578. DOI: 10.1016/j.energy.2011.07.015.

[27] JAIN R K, SMITH K M, CULLIGAN P J, TAYLOR J E. Forecasting energy consumption of multi-family residential buildings using support vector regression: Investigating the impact of temporal and spatial monitoring granularity on performance accuracy [J]. Applied Energy, 2014, 123: 168-178. DOI: 10.1016/j.apenergy.2014.02.057.

[28] MAMLOOK R, BADRAN O, ABDULHADI E. A fuzzy inference model for short-term load forecasting [J]. Energy Policy, 2009, 37(4): 1239-1248. DOI: 10.1016/j.enpol.2008. 10.051.

[29] ELIAS C N, HATZIARGYRIOU N D. An annual midterm energy forecasting model using fuzzy logic [J]. IEEE Transactions on Power Systems, 2009, 24(1): 469-478. DOI: 10.1109/TPWRS.2008.2009490.

[30] KUCUKALI S, BARIS K. Turkey’s short-term gross annual electricity demand forecast by fuzzy logic approach [J]. Energy Policy, 2010, 38(5): 2438-2445. DOI: 10.1016/ j.enpol.2009.12.037.

[31] KABOLI S H A, FALLAHPOUR A, SELVARAJ J, RAHIM N A. Long-term electrical energy consumption formulating and forecasting via optimized gene expression programming [J]. Energy, 2017, 126: 144-164. DOI: 10.1016/j.energy. 2017.03.009.

[32] CANYURT O E, OZTURK H K. Application of genetic algorithm (GA) technique on demand estimation of fossil fuels in Turkey [J]. Energy Policy, 2008, 36(7): 2562-2569. DOI: 10.1016/j.enpol.2008.03.010.

[33] ASSAREH E, BEHRANG M A, ASSARI M R, GHANBARZADEH A. Application of PSO (particle swarm optimization) and GA (genetic algorithm) techniques on demand estimation of oil in Iran [J]. Energy, 2010, 35(12): 5223-5229. DOI: 10.1016/j.energy.2010.07.043.

[34] GULCU S, KODAZ H. The estimation of the electricity energy demand using particle swarm optimization algorithm: A case study of Turkey [J]. Procedia Computer Science, 2017, 111: 64-70. DOI: 10.1016/j.procs.2017.06.011.

[35] ASKARZADEH A. Comparison of particle swarm optimization and other metaheuristics on electricity demand estimation: A case study of Iran [J]. Energy, 2014, 72: 484-491. DOI: 10.1016/j.energy.2014.05.070.

[36] TOKSAR M D. Ant colony optimization approach to estimate energy demand of Turkey [J]. Energy Policy, 2007, 35(8): 3984-3990. DOI: 10.1016/j.enpol.2007.01.028.

[37] TOKSAR M D. Estimating the net electricity energy generation and demand using the ant colony optimization approach: Case of Turkey [J]. Energy Policy, 2009, 37(3): 1181-1187. DOI: 10.1016/j.enpol.2008.11.017.

[38] NIU D, WANG Y, WU D D. Power load forecasting using support vector machine and ant colony optimization [J]. Expert Systems with Applications, 2010, 37(3): 2531-2539. DOI: 10.1016/j.eswa.2009.08.019.

[39] SONMEZ M, AKGUNGR, ALI PAYDAR, BEKTA S. Estimating transportation energy demand in Turkey using the artificial bee colony algorithm [J]. Energy, 2017, 122: 301-310. DOI: 10.1016/j.energy.2017.01.074.

[40] JIANG B B, CHEN W Y, YU Y F, ZENG L M, VICTOR D. The future of natural gas consumption in Beijing, Guangdong and Shanghai: An assessment utilizing MARKAL [J]. Energy Policy, 2008, 36(9): 3286-3299. DOI: 10.1016/j.enpol.2008. 04.031.

[41] MALLAH S, BANSAL N K. Allocation of energy resources for power generation in India: Business as usual and energy efficiency [J]. Energy Policy, 2010, 38(2): 1059-1066. DOI: 10.1016/j.enpol.2009.10.058.

[42] SHABBIR R, AHMAD S S. Monitoring urban transport air pollution and energy demand in Rawalpindi and Islamabad using leap model [J]. Energy, 2010, 35(5): 2323-2332. DOI: 10.1016/j.energy.2010.02.025.

[43] ATES S A. Energy efficiency and CO₂ mitigation potential of the Turkish iron and steel industry using the LEAP (long- range energy alternatives planning) system [J]. Energy, 2015, 90: 417-428. DOI: 10.1016/j.energy.2015.07.059.

[44] PAO H T, FU H C, TSENG C L. Forecasting of CO2 emissions, energy consumption and economic growth in China using an improved grey model [J]. Energy, 2012, 40(1): 400-409. DOI: 10.1016/j.energy.2012.01.037.

[45] BARAK S, SADEGH S S. Forecasting energy consumption using ensemble ARIMA–ANFIS hybrid algorithm [J]. International Journal of Electrical Power & Energy Systems, 2016, 82: 92-104. DOI: 10.1016/j.ijepes.2016.03.012.

[46] PAO H T. Forecasting energy consumption in Taiwan using hybrid nonlinear models [J]. Energy, 2009, 34(10): 1438-1446. DOI: 10.1016/j.energy.2009.04.026.

[47] LIU X, MORENO B, GARCA A S. A grey neural network and input-output combined forecasting model. Primary energy consumption forecasts in Spanish economic sectors [J]. Energy, 2016, 115: 1042-1054. DOI: 10.1016/j.energy. 2016.09.017.

[48] RAVADANEGH S N, OSKUEE M D R J KARIMI M. Multi-objective planning model for simultaneous reconfiguration of power distribution network and allocation of renewable energy resources and capacitors with considering uncertainties [J]. Journal of Central South University, 2017, 24(8): 1837-1849. DOI: 10.1007/s11771- 017-3592-8.

[49] TIMMERMAN J, VANDEVELDE L, van EETVELDE G. Towards low carbon business park energy systems: Classification of techno-economic energy models [J]. Energy, 2014, 75: 68-80. DOI: 10.1016/j.energy.2014.05.092.

[50] ZHAO H X, MAGOULS F. A review on the prediction of building energy consumption [J]. Renewable and Sustainable Energy Reviews, 2012, 16(6): 3586-3592. DOI: 10.1016/ j.rser.2012.02.049.

[51] MCPHERSON M, KARNEY B. Long-term scenario alternatives and their implications: LEAP model application of Panamas electricity sector [J]. Energy Policy, 2014, 68: 146-157. DOI: 10.1016/j.enpol.2014.01.028.

[52] ZHOU J, MAO X Q, HU T, ZENG A, XING Y, CORSETTI G. Implications of the 11th and 12th Five-Year Plans for energy conservation and CO₂ and air pollutants reduction: A case study from the city of Urumqi, China [J]. Journal of Cleaner Production, 2016, 112: 1767-1777. DOI: 10.1016/ j.jclepro.2015.08.015.

[53] CAI W, WANG C, CHEN J, WANG K, ZHANG Y, LU X. Comparison of CO₂ emission scenarios and mitigation opportunities in China′s five sectors in 2020 [J]. Energy Policy, 2008, 36(3): 1181-1194. DOI: 10.1016/j.enpol. 2007.11.030.

[54] OUEDRAOGO N S. Modeling sustainable long-term electricity supply-demand in Africa [J]. Applied Energy, 2017, 190: 1047-1067. DOI: 10.1016/j.apenergy.2016.12. 162.

[55] SADRI A, ARDEHALI M M, AMIRNEKOOEI K. General procedure for long-term energy-environmental planning for transportation sector of developing countries with limited data based on LEAP (long-range energy alternative planning) and energy plan [J]. Energy, 2014, 77: 831-843. DOI: 10.1016/j.energy.2014.09.067.

[56] NOJEDEHI P, HEIDARI M, ATAEI A, NEDAEI M, KURDESTANI E. Environmental assessment of energy production from landfill gas plants by using long-range energy alternative planning (LEAP) and IPCC methane estimation methods: A case study of Tehran [J]. Sustainable Energy Technologies and Assessments, 2016, 16: 33-42. DOI: 10.1016/j.seta.2016.04.001.

[57] KALE R V, POHEKAR S D. Electricity demand and supply scenarios for Maharashtra (India) for 2030: An application of long range energy alternatives planning [J]. Energy Policy, 2014, 72: 1-13. DOI: 10.1016/j.enpol.2014.05.007.

[58] LEONARDO P, LUPTON R C, CULLEN J M. Useful energy balance for the UK: An uncertainty analysis [J]. Applied Energy, 2018, 228: 176-188. DOI: 10.1016/ j.apenergy.2018.06.063.

[59] MARTIN N P D, BISHOP J D K, CHOUDHARY R, BOIES A M. Can UK passenger vehicles be designed to meet 2020 emissions targets? A novel methodology to forecast fuel consumption with uncertainty analysis [J]. Applied Energy, 2015, 157: 929-939. DOI: 10.1016/j.apenergy.2015.03.044.

[60] da SILVA F L C, OLIVEIRA F L C, SOUZA R C. A bottom-up bayesian extension for long term electricity consumption forecasting [J]. Energy, 2019, 167: 198-210. DOI: 10.1016/j.energy.2018.10.201.

[61] China Statistic Official agency. General administration of quality supervision, inspection and quarantine [M]. Beijing: China Standard Press, 2008. (in Chinese)

[62] MIRJAT N H, UQAILI M A, HARIJAN K, WALASAI G D, MONDAL M A H, SAHINJ H. Long-term electricity demand forecast and supply side scenarios for Pakistan (2015–2050): A LEAP model application for policy analysis [J]. Energy, 2018, 165: 512-526. DOI: 10.1016/j.energy. 2018.10.012.

[63] CCERES M O, CCERES-SAEZ I. Random Leslie matrices in population dynamics [J]. Journal of Mathematical Biology, 2011, 63(3): 519-556. DOI: 10.1007/s00285-010- 0378-0.

[64] THAWGAVELU S R, KHAMBADKONE A M, KARIMI I A. Long-term optimal energy mix planning towards high energy security and low GHG emission [J]. Applied Energy, 2015, 154: 959-969. DOI: 10.1016/j.apenergy.2015.05.087.

[65] Statistic Bureau of China. China statistical yearbook 2015 [M]. Beijing: China Statistical Press, 2015. (in Chinese)

[66] Statistic Bureau of Hunan Province. Hunan statistical yearbook 2013 [M]. Beijing: China Statistical Press, 2013. (in Chinese)

[67] Statistic Bureau of China. Compilation of New China's 55 years of statistics [M]. Beijing: China Statistical Press, 2005. (in Chinese)

[68] Statistic Bureau of Hunan Province. Hunan 2012 population census data [M]. Beijing: China Statistical Press, 2012. (in Chinese)

[69] Statistic Bureau of China. China 2010 census data [M]. Beijing: China Statistics Press, 2012. (in Chinese)

[70] Hunan's Development and Reform Commission. The 12th Five-Year Plan of economic, social and energy development in Hunan Province [M]. Changsha, 2011. (in Chinese)

[71] Hunan's Development and Reform Commission. The 13th Five-Year Plan of economic, social and energy development in Hunan Province [M]. Changsha, 2016. (in Chinese)

[72] SUBRAMANYAM V, PARAMSHIVAN D, KUMAR A, MONDAL M A H. Using Sankey diagrams to map energy flow from primary fuel to end use [J]. Energy Conversion and Management, 2015, 91: 342-352. DOI: 10.1016/ j.enconman.2014.12.024.

(Edited by YANG Hua)

中文导读

数据有限区域中长期能源需求预测的混合LEAP建模方法

摘要：准确的长期能源需求预测对于能源规划和决策至关重要。然而，由于能源数据收集和统计方法不完善，许多区域的可用于能源需求预测的数据通常有限。本文在文献综述的基础上，提出了一种基于长期替代能源规划模型(LEAP)的混合建模方法，以提高这些区域能源需求预测的准确性。以中国湖南省为例，应用该混合模型对不同行业未来可能的能源需求和节能潜力进行了估算。基于Sankey能流图确定LEAP模型结构，采用Lesline矩阵和自回归移动平均(ARIMA)模型分别预测人口、产业结构和运输周转率。采用蒙特卡罗方法评估预测结果的不确定性。研究结果表明，混合模型结合情景分析对统计数据有限区域的长期能源需求提供了相对准确的预测，2030年基础情景下能源需求概率分布的平均标准差不超过0.15。预测结果可为识别节能潜力和制定能源发展路径提供参考依据。

关键词：有限数据能源需求预测；混合LEAP模型；ARIMA模型；Leslie矩阵；蒙特卡罗法

Foundation item: Project(51606225) supported by the National Natural Science Foundation of China; Project(2016JJ2144) supported by Hunan Provincial Natural Science Foundation of China; Project(502221703) supported by Graduate Independent Explorative Innovation Foundation of Central South University, China

Received date: 2019-06-10; Accepted date: 2019-07-15

Corresponding author: LIAO Sheng-ming, PhD, Professor; Tel: +86-731-88879863; E-mail: smliao@csu.edu.cn; ORCID: 0000-0002- 0802-5072