Deformed texture of copper processed by equal channel angular pressing via different angle routes

WU Bao-lin(武保林)¹, HUANG Zhen-wei(黄震威)¹,

ZHANG Yu-dong(张宇东)^{1, 2}, BAO Lei(宝 磊)¹ , C. ESLING²

1. Department of Materials Engineering, Shenyang Institute of Aeronautical Engineering, Shenyang 110034, China;

2. LETAM, CNRS-UMR 7078, University of Metz, Ile du Saulcy, 57045 Metz, France

Received 1 December 2006; accepted 2 April 2007

Abstract: The commercially pure copper with dimension of 80 mm×20 mm×4 mm was used for equal channel angular pressing (ECAP), of which their outward appearance coordinate is corresponded with that of rolling deformation modes. Cold-deformed texture was investigated. The results show that the texture character in pure copper processed by ECAP is related with intersection angle (F) of the die channel. When F is 90? and the sample is extruded for one pass, its texture consists of α and b orientation lines including mainly C, B, S and Goss components, moreover a little rotated cube is found. When F is 135?, as extrusion pass increases, the weak texture forms on the scope of deviation from rotated cube (y=0?, θ=0?, j=45?±15?) and develops to the y=45? fiber mainly including rotated cube. When F is 120?, the texture is y=45? fiber mainly including rotated cube that is maintained constant as extrusion pass increases.

Key words: equal channel angular pressing; texture; deformation; multi-slip

1 Introduction

The process of equal channel angular pressing (ECAP) was originally described by SEGAL et al[1-2]. As a severe deformation technique, ECAP plays an effective role in making ultrafine grain materials. The researches on mechanics [3-4], microstructure[5-7] and mechanical properties [8-9] were reported previously. There has also been much interest in the texture formation during ECAP deformation[10-12]. With the ECAP process, material can be deformed to very high strains without any significant decrease in cross-sectional area, resulting in various combination of mechanical properties, grain size and texture. Changing the processing route effectively changes the strain path to which the material is subjected during deformation. Therefore different combinations of grain size, grain shape and texture can be obtained. Different texture features were reported for different ECAP routes[13-16]. To investigate the characteristics of deformed texture in materials processed by ECAP is helpful to better under-stand texture formation mechanisms and grains refinement process. Copper with FCC structure is previously one of dominant materials for studying cold-rolled and recrystallized texture mechanisms. Strain paths during ECAP and rolling are quite different, so textures obtained by the two kinds of process are also different. Comparison of texture evolution during ECAP with that during rolling deformation modes is of significance. Therefore further study of both the microstructural and textural evolution during the ECAP process is of interest. In early researches, most samples were columnar, the textures had to be characterized by pole figures or two-dimensional electronic back scattering patterns(EBSP) figures. In present work the sheet samples of commercially pure copper were adopted, of which their outward appearance coordinate was corresponded with that of rolling conditions. Cold-deformed texture characteristics via different angle routes were investigated with orientation distribution function(ODF) analysis. The formation mechanism of texture was discussed.

2 Experimental

The original samples of commercially pure copper with dimension of 80 mm×20 mm×4 mm were used in the experiment. Very random texture was found in the original samples. Three different kinds of ECAP dies respectively with channel intersection angles F=135?, 120? and 90? were adopted (Figs.1(a) and (b)). The curvature of outer arc where the two channels intersect was very sharp, i.e. Y was near zero. After extrusion at room temperature, texture was detected by X-ray diffractometer. Extrusion direction p was corresponding to rolling direction R of rolling deformation conditions. The crosswise T_p was corresponding to rolling transverse direction T and normal direction of wide surface N_p is corresponding to rolling plane N (Fig.1(c)). The extrusion was carried on by route A, but in which the samples were up-down set repeatedly.

A layer with 2.0 mm in thickness was removed off from the wide surface U of the samples and texture on this side was detected. Texture was measured with the DX-2000 X-ray diffractometer. Cu K_α radiation was selected and Ni filtration sheet was used. The tube voltage was 40 kV and the tube current was 30 mA. The X-ray source aperture was 2? (diffraction slit, DS). The receiving apertures were 5 mm (receive slit, RS) and 5 mm (speckle-prevented slit, SS). The three incomplete pole figures of {111}, {200} and {220} were detected by means of Schulz back-diffraction. The angle ranges were α: 90?-20?; β: 0?-360? and the angle step was 5?. The two step method was adopted to calculate ODF. The maximum item number of series expansion(I_max) was 16. ODF was expressed by constant ψ or j sections figure, where y, θ and j are respectively Eular angles (Roe symbol).  SEM-EBSP technique was used to observe orientation image of microstructure and analyze grain boundary character distribution(GBCD). TEM was used to observe submicrostructure in longitudinal section of the samples.

3 Results and discussion

When passing through a die, the distortion of material is approximately pure shear. When curvature angle Ψ of outer arc in the channel is zero, strain can be expressed as follows[17]:

where  F is the intersection angle of the channel. For F=135?, 120? and 90?, the material has respectively strain of 0.48, 0.67 and 1.16 when extruded through the channel for one pass.

While the intersection angle F is 135? and the sample is extruded for one pass, the orientation distributes mainly on the scope of deviation from rotated cube position (y=0?, θ=0?, j=45?) symmetrically (j= 45?±15?) (Fig.2(a)). For 5 passes (route A), the sample shows mainly rotated cube component ({001}<110>) in Fig.2(b).

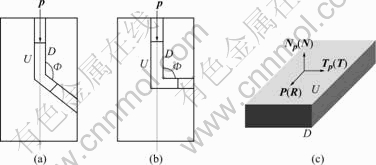
Fig.1 Schematic diagrams of ECAP extrusion way: (a) F=120? or 135?; (b) F=90?; (c) Coordinates of samples

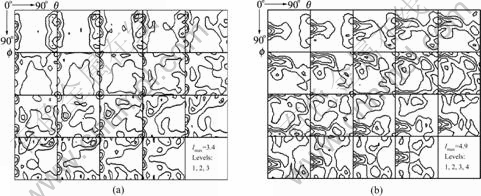
Fig.2 Constant y (Dy=5?) sections of ODFs of copper processed by ECAP with F=135?: (a) One pass; (b) Five passes

Furthermore it was found that the texture is fiber of y=45° including rotated cube in the constant j sections of ODF of the sample that is extruded for five passes in the die with F=135? (Fig.3). Moreover weak brass component was also found (the arrow refers).

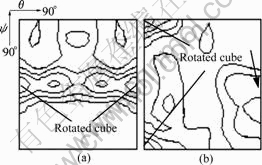
Fig.3 Constant j sections of ODF of copper processed by ECAP with F=135? for five passes: (a) φ=0; (b) φ=45?

When the intersection angle F is 120? and the sample is extruded for one pass, texture shows also mainly rotated cube component. Fig.4 is constant y (Dy=5?) sections of ODFs of the samples extruded for 1, 5, 8and 12 passes, respectively. It can be seen that the texture intensity increases slightly when extrusion is from one pass to 5 passes, but even to 12 passes, the texture nearly maintains constant. Nevertheless, the texture keeps the same characteristics in this case.

Fig.4 Constant ψ (?ψ=5?) sections of ODFs of copper processed by ECAP with Φ=120?: (a) One pass; (b) Five passes; (c) 8 passes; (d) For 12 passes

When intersection angle F of the die is 90? and the sample is extruded for one pass, texture characteristics is different from the above. In Fig.5 it can be found that the texture is just similar to cold rolled one consisting of α and β orientation lines that include mainly C ({112} <111>), B ({110}<112>), weak S ({123}<634>) and weak Goss. Weak rotated cube component was also found.

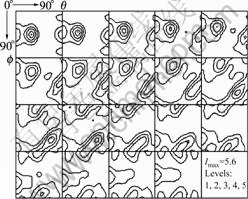
Fig.5 Constant ψ (?ψ=5?) sections of ODF of copper processed for one pass by ECAP with Φ=90?

The high resolution SEM-EBSP technique was used to observe microstructure of the samples. According to Brandon criterion, grain boundary character distribution (GBCD) was calculated by analysis software on SEM instrument. Coincidence site lattice(CSL) grain boundaries are marked by black lines (Figs.6(a), (b) and (c)). When the die angle F of intersection is 135? and the sample is extruded for one pass, it was found that the majority of primitive CSL grain boundaries are maintained because of small strain (0.48) applied. The of twins (Fig.6(d)). When extruded for 5 passes, as strain increases, special CSL orientation relations are destructed and grains are refined (Fig.6(b)). When the die angle F of intersection is 90?, the special orientation relations are already destructed as the sample is extruded just for one pass. The microstructure observed from the longitudinal section of the sample becomes elongate and the CSL grain boundaries are broken off (Fig.6(c)). At the same time the inhomogeneous shear bands(SBs) are formed. As the grains are refined and grain boundaries are broken off, grains orientation must be changed, so the orientation distribution forms.

Fig.6 EBSP orientation microscopy maps of copper processed by ECAP and frequencies of CSL grain boundaries: (a) F=135?, one pass, normal section; (b) F=135?, 5 passes, normal section; (c) F=90?, one pass, longitudinal section; (d) Frequencies of CSL grain boundaries in Fig.6(a)

Deformation texture of polycrystals can be simulated with Taylor, Sachs and Intermediate Models [17]. Taylor’s theory has been successful in qualitative prediction of crystallographic textures  development for FCC and BCC metals, but the rotation matrix in the model is not connected with the evolution of microstructures in detail. GORAN et al[14] investigated Ni single crystal deformation by ECAP with F=90? for which <100> was set parallel to P, N_p and T_p respectively. The results show that in the central zone, the deformation texture can almost be obtained from the original cube orientation by the combined rotations of 45? about the transverse direction T_p and along the macroscopic shear direction. The microstructure is characterized by a matrix containing parallel bands. The grains are inclined about 35? with regard to P. In present experiment, a grain of the polycrystals may rotate by the similar way. Deformed texture is connected closely with the microstructure development of materials. During deformation, the primitive disorientation relation is destructed and grains refinement is followed by orientation differentiation. A grain will split, resulting in its orientation manifold. For regularly deformation there will be texture formed and it concentrates and stabilizes on some special orientations.

We know that rotated cube is a main component of the samples pressed through the die with F=135? and 120?. C and B are main components of the sample processed for one pass through the die with F=90?. In the distortion process, those grains with slip system orientation near to the shear direction deforms first, thus slipping on {111} plane is started. Fig.7 shows that schematic diagram of relationship between the samples coordinates and some orientations in (110) stereographic projection where [110]//T_p. The 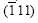 plane is laid parallel to the shear direction, therefore R₁ON₁ and R₂ON₂ are respectively corresponding to the coordinates of the samples processed with the die where F is 90? and 135?. The angles between N and shear direction is 67.5? and 45?, respectively for F=135? and F=90? conditions. 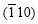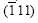It can be seen that (001),  and   belong to the same crystalline zone with [110] axis. If the crystallite were rotated around T_p, rotated cube  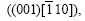C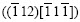 and Goss ((110)<001>) components would be obtained directly. For F=135? case, if a grain with  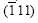parallel to macroscopic shear direction deforms first, it will splits and rotates around [110] (T_p) to (001)//N_p position, therefore metastable rotated cube can be easy obtained. Its original orientation is approximately 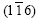//N_p. For F=90? case, the orientation of a grain which will rotate first is approximately 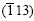//N_p. If multi-slip were  started, the crystallite would rotate around [110] and also 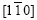, therefore  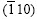would  get parallel to N_p and  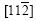parallel to P, so component B would be obtained. But from Fig.7 it can be found that this process requires big rotation angle, e.g. large strain.

For low strained samples, low density dislocation can be observed under TEM (Fig.8(a)). As deformation continues (extrusion pass increases to 5), density dislocation increases to form dislocation cells and subgrains inhomogeneously shown in Fig.8(b). The deformed microstructure is characterized by lamellar shape (Fig.8(c)) which is usually considered as microbands(MBs). There also exists equiaxial substruc- tures in MBs. Fig.8(d) shows equiaxial subgrains in MBs of the extruded sample with the 120? ECAP die. The electronic diffraction pattern of the subgrains indicates that <110> is parallel to T_p direction in this case, so the progress of grains splitting by rotation around <110> can be assumed. In Fig.9 it can be also found that the <110>//T_p orientation crystallites exit in deforming bands.

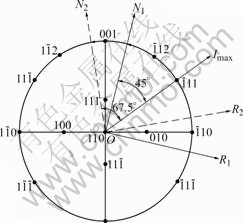
Fig.7 Schematic diagram of relationship between samples coordinates and some orientations in (110) stereographic projection

Fig.8 Deformed microstructures under TEM observation (longitudinal section): (a) Low density dislocation in sample extruded for one pass, F=135?; (b) Inhomogeneous deformation microstructure in sample extruded for five passes, F=135?; (c) Microbands in sample extruded for five passes, F=135?; (d) Equiaxial subgrains in microbands and electronic diffraction pattern in sample extruded for five passes, F=120?

Fig.9 Orientation image of microstructure of longitudinal section in deformed sample by ECAP with 120? intersection angle Φ for five passes

As we know that in polycrystals, a grain orientation splits followed by crystallites rotation to form subgrain boundaries. A subgrain boundary with small disorientation is considered as a dislocation wall. In copper, if [112] on 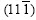 and  is nearly parallel to the shear direction, double slip is possible to take place. So a/2<110> dislocation on different {111} planes will react to perform a new fixed a/2<110> unit dislocation as

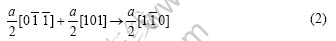
or

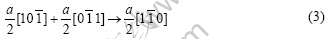
Therefore the produced dislocations will construct dislocation boundary resulting in the crystallites rotating as expressed in Fig.10. If the unit dislocation is the expansion dislocation during double slipping process, then Lomer-Cottrell fixed dislocation may be produced.

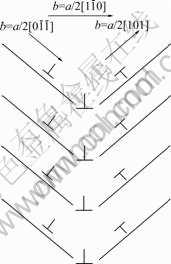
Fig.10 Schematic diagram of subgrain boundry formation through dislocations reaction

Discussion above shows the formation of main texture components of rotated cube, C and B in ECAP, but slip direction in Schimdt factor by no means is considered. For the sample extruded for one pass with 135? ECAP die, the orientation distribution mainly and weakly concentrates on the scope of deviation from the rotated cube position. If slip direction and slip plane are considered simultaneously as parallel to shear direction and the crystallite rotates around T_p, this orientation can be approximately obtained. Shear stress and strain needed in this case are neither large. Further analysis needs to make a simulation combined with Taylor model.

4 Conclusions

1) Texture characteristics in pure copper processed by ECAP is related with intersection angle of the channel in a die. While F is 90? and the sample is extruded for one pass, its texture consists of α and β orientation lines including mainly C, B, S and Goss components, moreover also a little rotated cube is found. When F is 135?, as extrusion pass increases, weak texture forms on the scope of deviation from rotated cube (y=0?, θ=0?, j=45?±15?) and develops to y=45? fiber mainly including rotated cube. When F is 120?, texture is y=45? fiber mainly including rotated cube which is maintained constant as extruding pass increases.

2) The dislocation multi-slip during deformation produces the dislocation reaction. This contributes a grains’ orientation splitting and subgrain boundaries forming to crystallites rotation. The cold-deformed texture formation is related with this course.

References

[1] SEGAL V M. Methods of stress strain analysis in metal forming, Sc [D]. Minsk: Acad of Sciences of the Belorussian SSR, Physicotechnical Inst, USSR, 1974. (in Russian)

[2] SEGAL V M, REZNIKOV V I, DROBYSHEVSKIY A E, KOPYLOV V I. Plastic metal working by simple shear [J]. Izvestiya AN SSSR: Metally, 1981(1): 115-123. (in Russian)

[3] SEGAL V M. Equal channel angular extrusion: From macro- mechanics to structure formation [J]. Materials Science and Engineering A, 1999, A271: 322-333.

[4] FURUKAWA M, IWAHASHI Y, HORITA Z, NEMOTO M, LANGDON T G. The shearing characteristics associated with equal channel angular pressing [J]. Materials Science and Engineering A, 1998, A257: 328-332.

[5] BAIK S C, ESTRIN Y, KIM H S, HELLMIG R J. Dislocation density-based modeling of deformation behavior of aluminium under equal channel angular pressing [J]. Materials Science and Engineering A, 2003, A351: 86-97.

[6] ZHU Y T, LOWE T C. Observation and issues on mechanisms of grain refinement during ECAP process [J]. Materials Science and Engineering A, 2000, A291: 46-53.

[7] SHAN A D, MOON I G, HUNG S K, JONG W P. Direct observation of shear deformation during equal channel angular pressing of pure aluminum [J]. Scripta Materialia, 1999, 41: 353-357.

[8] XU C, DIXON W, FURUKAWA M, HORITA Z, LANGDON T G. Developing superplasticity in a spray-cast aluminum 7034 alloy through equal-channel angular pressing [J]. Materials Letters, 2003, 4386: 1-5.

[9] STOLYAROV V V, ZHU Y T, LOW T C, VALIEV R Z. Microstructure and properties of pure Ti processed by ECAP and cold extrusion [J]. Materials Science and Engineering A, 2001, A303: 82-89.

[10] PITHAN C, HASHIMOTO T, KAWAZOE M, NAGAHORA J, HIGASHI K. Microstructure and texture evolution in ECAE processed A5056 [J]. Materials Science and Engineering A, 2000, A280: 62-68.

[11] CAO W Q, GODFREY A, LIU Q. EBSP investigation of microstruc- ture and texture evolution during equal channel angular pressing of aluminium [J]. Materials Science and Engineering A, 2003, A361: 9-14.

[12] CHAKKINGAL U, SURIADI A B, THOMSON P F. The development of microstructure and the influence of processing route during equal channel angular drawing of pure aluminum [J]. Materials Science and Engineering A, 1999, A266: 241-249.

[13] SUH J Y, HAN J H, OH K H, LEE J C. Effect of deformation histories on texture evolution during equal- and dissimilar-channel angular pressing [J]. Scripta Materialia, 2003, 49: 185-190.

[14] GORAN D, FUNDENBERGER J J, SUWAS S, BOUZY E, TOTH L, SKROTZKI W, GROSDIDIER T. Pure Ni single crystal of cube orientation deformed by equal channel angular extrusion [J]. Solid State Phenomena, 2005, 105: 333-338.

[15] KUSNIERZ J. Rolling texture of ECAP processed Al and Cu [J]. Solid State Phenomena, 2005, 105: 339-344.

[16] SUWAS S, TOTH L, FUNDENBERGER J J, GROSDIDIER T, SKROTZKI W. Texture evolution in FCC metals during equal channel angular extrusion (ECAE) as a function of stacking fault energy [J]. Solid State Phenomena, 2005, 105: 345-350.

[17] KAMACHI M, FURUKAWA M, HORITA Z, LANGDON T G. A model investigation of the shearing characteristics in equal-channel angular pressing [J]. Materials Science and Engineering A, 2003, A347: 223-230.

Foundation item: Project(Lnzr0201) supported by the Foundation of Science and Technology Committee of Liaoning Province of China

Corresponding author: WU Bao-lin; Tel: +86-24-89723976; E-mail: wubaolin02@yahoo.com.cn

(Edited by YANG Hua)