DOI: 10.11817/j.ysxb.1004.0609.2020-37526
不同加载方向时轧制态AZ31镁合金高速变形行为的实验研究与数值模拟
陈 扬,毛萍莉,王 志,刘 正,王瑞峰
(沈阳工业大学 材料科学与工程学院,沈阳 110870)
摘 要:为研究轧制态AZ31镁合金在高应变率变形条件下的各向异性,沿镁合金板材的法向(ND)、45°方向和轧制方向(RD)分别进行应变速率700 s-1、1000 s-1、1300 s-1和1600 s-1的分离式霍普金森压杆(SHPB)实验。根据实验结果拟合得出不同加载方向下的Johnson-Cook本构方程。应用有限元分析专用前处理软件Hypermesh与显式动力学仿真软件LS-DYNA对SHPB实验过程进行数值模拟。实验与数值模拟结果表明:轧制态AZ31镁合金在高应变率条件下沿轧制方向加载时具有更强的变形能力且真应力-真应变曲线存在明显的屈服阶段;沿法向加载时表现出更明显的正应变速率强化效应和应变速率敏感性。数值模拟后处理所得真应变-时间曲线和真应力-真应变曲线与SHPB实验结果吻合度较高。不同加载方向下AZ31镁合金的Johnson-Cook本构方程参数均具有较高的拟合精度。
关键词:AZ31镁合金;高速变形;各向异性行为;Johnson-Cook本构方程;数值模拟
文章编号:1004-0609(2020)-05-0997-13 中图分类号:TG146.2 文献标志码:A
镁合金具有比强度高、密度低、阻尼减震性能好、导热性能优良和易于回收等诸多优点,在汽车、电子、国防军工和航空航天等领域得到了日益广泛的应用[1]。作为目前应用最广泛的变形镁合金,AZ31成品零部件在不同使用条件下所受到的载荷也不尽相同。除静载荷和准静态载荷外,在某些特殊工况下还不可避免地会受到高速冲击载荷的作用,比如高速切削、爆炸及侵彻等复杂动态场合[2]。
由于镁及其合金特殊的密排六方(hexagonal close- packed)晶体结构,室温下独立滑移系少导致其塑性变形能力低,使镁及其合金在轧制或挤压过程中形成较强的基面织构,从而在力学性能上表现出明显的各向异性[3-4]。CHINO等[5]在温度为25~400 ℃范围内对挤压态AZ31镁合金进行单轴拉伸与压缩实验,并对初始织构和温度引起镁合金力学性能的各向异性进行分析,指出AZ31镁合金的各向异性程度随晶粒尺寸的减小和温度的升高逐渐减弱。WATANABLE等[6]研究了应变速率在1×103 s-1的高速冲击载荷下初始织构对AZ31镁合金高温变形行为的影响。结果表明,具有丝织构(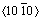 )的挤压态AZ31镁合金在所测试的各个温度下均具有明显的各向异性。具体表现为:纵向试样的屈服应力对温度的依赖关系远小于横向试样的,且横向试样的屈服强度小于纵向试样的屈服强度。CHEN等[7]对不同厚度的AZ31镁合金轧制板材在室温条件下进行不同取向的拉伸与压缩实验,结果表明沿板材横向的抗压及抗拉屈服强度明显高于板材轧制方向的,且不同取向的抗压屈服强度明显小于抗拉屈服强度。这是由于拉伸孪晶会导致晶粒绕c轴偏转,所以当应力垂直于基面时,难以产生
)的挤压态AZ31镁合金在所测试的各个温度下均具有明显的各向异性。具体表现为:纵向试样的屈服应力对温度的依赖关系远小于横向试样的,且横向试样的屈服强度小于纵向试样的屈服强度。CHEN等[7]对不同厚度的AZ31镁合金轧制板材在室温条件下进行不同取向的拉伸与压缩实验,结果表明沿板材横向的抗压及抗拉屈服强度明显高于板材轧制方向的,且不同取向的抗压屈服强度明显小于抗拉屈服强度。这是由于拉伸孪晶会导致晶粒绕c轴偏转,所以当应力垂直于基面时,难以产生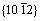 拉伸孪晶,导致载荷垂直于基面方向具有更大的屈服强度。石宝东等[8]对不同厚度的AZ31镁合金轧制板材沿不同方向进行常温单向拉伸和压缩实验,基于实验结果及晶体学塑性理论分析了不同轧制工艺对板材力学性能各向异性及拉压不对称性行为的影响。本课题组前期采用分离式Hopkinson压杆在平均应变速率为500~2600 s-1下对挤压态AZ31镁合金进行高速冲击压缩实验,并采用金相显微镜观察压缩后镁合金的组织演变规律,结果表明AZ31镁合金微观组织变化对应变速率非常敏感;在高应变速率下的变形机制除了孪晶之外,柱面滑移和锥面滑移也在一定程度上协调变形[9]。目前关于镁合金高速变形过程数值模拟方面的研究还相对较少。周霞等[10]基于SHPB的实验结果构建了Johnson-Cook本构模型,并根据所建立的模型对AZ91D镁合金的高速冲击过程进行了数值模拟,发现数值模拟结果与实验结果基本吻合。郭鹏程等[11]对AM80镁合金的高速变形行为进行了数值模拟,并将计算得到的应力-应变曲线与实验结果进行了比较。
拉伸孪晶,导致载荷垂直于基面方向具有更大的屈服强度。石宝东等[8]对不同厚度的AZ31镁合金轧制板材沿不同方向进行常温单向拉伸和压缩实验,基于实验结果及晶体学塑性理论分析了不同轧制工艺对板材力学性能各向异性及拉压不对称性行为的影响。本课题组前期采用分离式Hopkinson压杆在平均应变速率为500~2600 s-1下对挤压态AZ31镁合金进行高速冲击压缩实验,并采用金相显微镜观察压缩后镁合金的组织演变规律,结果表明AZ31镁合金微观组织变化对应变速率非常敏感;在高应变速率下的变形机制除了孪晶之外,柱面滑移和锥面滑移也在一定程度上协调变形[9]。目前关于镁合金高速变形过程数值模拟方面的研究还相对较少。周霞等[10]基于SHPB的实验结果构建了Johnson-Cook本构模型,并根据所建立的模型对AZ91D镁合金的高速冲击过程进行了数值模拟,发现数值模拟结果与实验结果基本吻合。郭鹏程等[11]对AM80镁合金的高速变形行为进行了数值模拟,并将计算得到的应力-应变曲线与实验结果进行了比较。
虽然对于镁合金高速变形行为的实验研究日益增多,但有关AZ31镁合金在高速冲击载荷下本构参数各向异性及数值模拟的研究还很少。本文应用SHPB实验装置在室温下对三种不同加载方向的轧制态AZ31镁合金圆柱状试样进行多组应变速率的高速冲击实验,研究不同加载方向和应变速率下轧制态AZ31镁合金的高速变形行为以及Johnson-Cook本构参数的各向异性。联合应用有限元分析专用前处理软件Hypermesh和显式动力学模拟软件LS-DYNA对SHPB实验进行数值模拟,并对实验结果、拟合结果和数值模拟结果进行对比验证。
1 实验
实验材料采用厚度为8 mm的轧制态AZ31 (Mg-3%Al-1%Zn-0.2%Mn)商用镁合金板材,轧制温度为350 ℃。经300 ℃、120 min的退火去孪晶处理后采用线切割方式沿板材法线方向(ND)、板法线夹角45°方向(45°)和板材轧制方向(RD)获得圆柱状试样(如图1所示)。试样规格为d 8 mm×6 mm,各表面粗糙度均为1.6 μm。
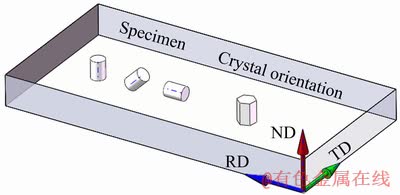
图1 AZ31镁合金板材取样示意图
Fig. 1 Sampling sketch map of rolled AZ31 magnesium alloy sheet
基于EBSD后处理的轧制态AZ31镁合金取向成像图与极图如图2所示。由图2(a)的取向成像图可知镁合金板材中晶粒尺寸分布较均匀,平均晶粒尺寸15.93 μm,且组织中未见明显孪晶;由图2(b)极图可知,材料具有强烈的{0001}基面织构,最大极密度值为14.37。
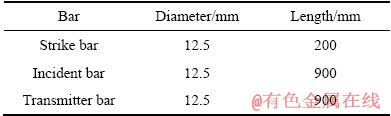
分离式霍普金森压杆(SHPB)实验装置的原理及操作方法详见参考文献[12],本文中SHPB实验装置中的冲击杆(Strike bar)、入射杆(Incident bar)、透射杆(Transmitter bar)的几何尺寸见表1。
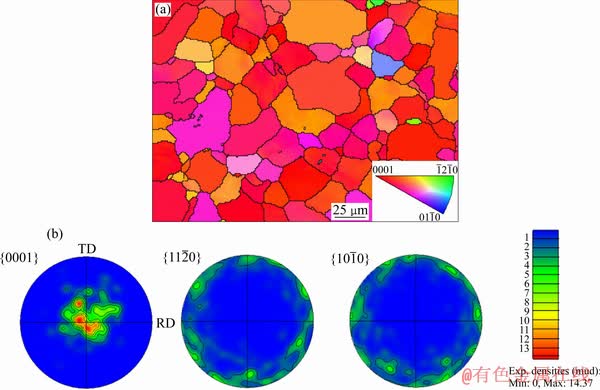
图2 实验用轧制态AZ31镁合金板材的取向成像图与极图
Fig. 2 Orientation map(a) and pole figures(b) of rolled AZ31 magnesium alloy sheet used for experiment
表1 冲击杆、入射杆、透射杆的几何尺寸
Table 1 Geometric dimensions of strike bar, incident bar and transmitter bar
SHPB实验通过记录入射杆及透射杆中的应力波,并根据一维波理论,按以下公式计算出试样所受到的应力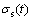 、应变
、应变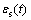 及应变速率
及应变速率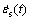 :
:
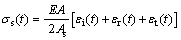 (1)
(1)
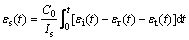 (2)
(2)
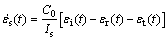 (3)
(3)
式中: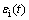 、
、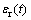 与
与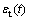 分别表示入射杆与透射杆表面应变片测得的应变值;C0为压杆的一维弹性波速,可通过
分别表示入射杆与透射杆表面应变片测得的应变值;C0为压杆的一维弹性波速,可通过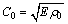 计算得出,
计算得出,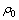 为压杆密度;Is与As分别表示试样的长度和横截面积;A和E分别表示压杆的横截面积和弹性模量[13-14]。
为压杆密度;Is与As分别表示试样的长度和横截面积;A和E分别表示压杆的横截面积和弹性模量[13-14]。
对ND、45°和RD三种加载方向的AZ31镁合金试样分别进行应变速率为700 s-1、1000 s-1、1300 s-1和1600 s-1的SHPB实验,在实验前对试样与压杆的接触端面涂抹少量二硫化钼锂基润滑脂,从而降低接触端面处的摩擦干扰以提高实验精度。AZ31镁合金沿不同加载方向和不同应变速率下的真应力-真应变曲线如图3所示。
对比图3中的各组真应力-真应变曲线可知,当应变速率在700~1600 s-1范围内变化时,各条曲线均呈连续光滑状态。载荷方向为RD时真应力-真应变曲线形态为凹型,曲线初始部分出现了较为明显的转折台阶,呈现出显著的屈服特征,流变应力在应变为0.025时的上升速率显著提高,说明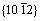 拉伸孪晶在该应变时开始产生[15]。当载荷方向为ND和45°时真应力-真应变曲线分别为凸型和近似直线型,未呈现出明显的屈服阶段。
拉伸孪晶在该应变时开始产生[15]。当载荷方向为ND和45°时真应力-真应变曲线分别为凸型和近似直线型,未呈现出明显的屈服阶段。
轧制态AZ31镁合金沿不同加载方向SHPB实验过程中弹性变形阶段(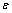 =0.001)和塑性变形阶段(
=0.001)和塑性变形阶段(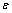 =0.05)真应力随应变速率的变化关系如图4所示。
=0.05)真应力随应变速率的变化关系如图4所示。
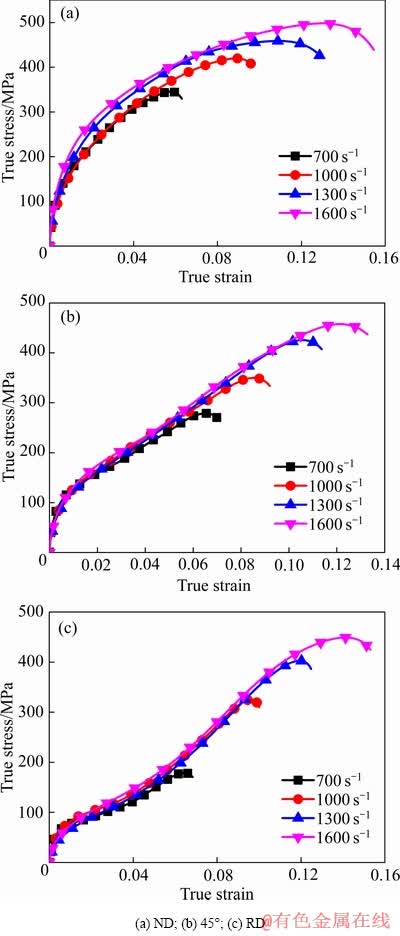
图3 轧制态AZ31镁合金沿不同加载方向下的真应力-真应变曲线
Fig. 3 True stress-strain curves of rolled AZ31 magnesium alloy loaded along different directions
由图4可知,当载荷方向为ND时,应变速率在700~1600 s-1范围内 =0.001的真应力从54.5 MPa增加至60 MPa,增幅为10%;
=0.001的真应力从54.5 MPa增加至60 MPa,增幅为10%; =0.05的真应力从333.9 MPa增加至384.8 MPa,增幅为15.2%,弹性变形和塑性变形阶段均呈现出正应变速率强化效应。而当载荷方向为45°时,同一应变速率范围内弹性变形阶段和塑性变形阶段的真应力增幅分别为3.5%和5.6%,正应变速率强化效应减弱。当载荷方向为RD时,弹性变形和塑性变形阶段正应变速率强化效应进一步弱化,真应力增幅分别仅为2.4%和3.1%。由此可知相比于加载方向为ND和45°,沿RD加载时达到相同应变所需应力最小,此时材料具有更强的变形能力。
=0.05的真应力从333.9 MPa增加至384.8 MPa,增幅为15.2%,弹性变形和塑性变形阶段均呈现出正应变速率强化效应。而当载荷方向为45°时,同一应变速率范围内弹性变形阶段和塑性变形阶段的真应力增幅分别为3.5%和5.6%,正应变速率强化效应减弱。当载荷方向为RD时,弹性变形和塑性变形阶段正应变速率强化效应进一步弱化,真应力增幅分别仅为2.4%和3.1%。由此可知相比于加载方向为ND和45°,沿RD加载时达到相同应变所需应力最小,此时材料具有更强的变形能力。
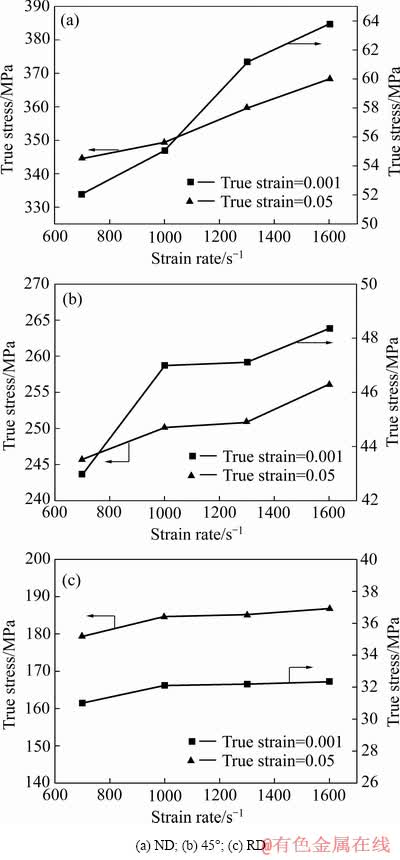
图4 轧制态AZ31镁合金沿不同加载方向下弹性和塑性变形阶段真应力与应变速率的关系
Fig. 4 Relationships between true stress and strain rate of rolled AZ31 magnesium alloy loaded along different directions during elastic and plastic deforming stages
轧制态AZ31镁合金沿不同加载方向的屈服应力与峰值应力随应变速率的变化规律如图5所示。由图中可以看出,三种不同加载方向下AZ31镁合金的屈服应力与峰值应力均随应变速率的增加而增大。RD加载方向下的峰值应力平均增幅最大,ND加载方向下峰值应力的平均增幅最小;在相同的应变速率下,ND加载方向下峰值应力和屈服应力值最大,RD加载方向下峰值应力和屈服应力值最小。
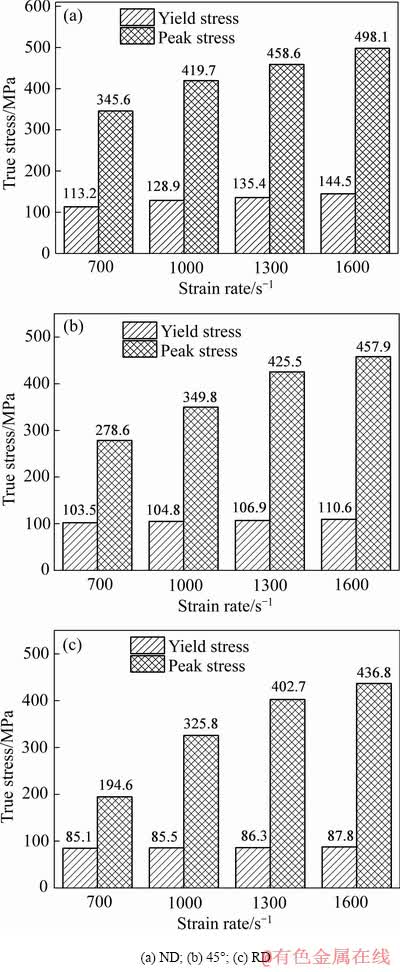
图5 轧制态AZ31镁合金沿不同加载方向下的峰值应力和屈服应力与应变速率的关系
Fig. 5 Relationships between peak stress, yield stress and strain rate of rolled AZ31 magnesium alloy loaded along different directions
图6所示为不同加载方向下轧制态AZ31镁合金不同应变速率的应变硬化率-真应变曲线。
由图6可知,高速冲击载荷沿ND、45°、RD时的应变硬化率-真应变曲线虽然在形态上有所差异,但大致均可划分为三个不同的阶段。第一阶段:应变硬化率均随真应变的增加急速降低;第二阶段:应变硬化率在ND、45°和RD加载方向下分别表现为缓慢下降、近似水平不变和持续上升,且这一阶段所覆盖的真应变范围随应变速率的增加而增大。相比于45°和RD加载方向的应变硬化率-真应变曲线,ND加载方向应变硬化率-真应变曲线的第二阶段并不明显,曲线仍呈现持续下降趋势,而45°和RD加载方向均存在明显区别于“第一阶段”的“第二阶段”。由于轧制态AZ31镁合金沿RD加载冲击载荷时在塑性变形阶段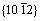 /
/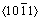 拉伸孪晶体积分数随着应变量的增大持续升高,从而使其第二阶段的应变硬化效应更加明显。第三阶段:在这一阶段不同加载方向轧制态AZ31镁合金的应变硬化率随真应变的增加均呈现出逐渐降低的趋势。
拉伸孪晶体积分数随着应变量的增大持续升高,从而使其第二阶段的应变硬化效应更加明显。第三阶段:在这一阶段不同加载方向轧制态AZ31镁合金的应变硬化率随真应变的增加均呈现出逐渐降低的趋势。
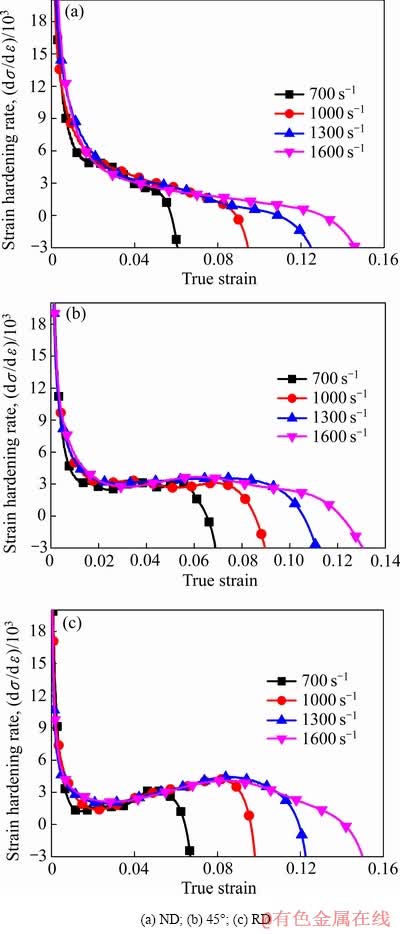
图6 轧制态AZ31镁合金沿不同加载方向下的应变硬化率-真应变曲线
Fig. 6 Strain hardening rate-true strain curves of rolled AZ31 magnesium alloy loaded along different directions
为更好地对比研究轧制态AZ31镁合金应变速率敏感性的各向异性,引入应变速率敏感指数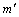 ,其表达式如下[16]:
,其表达式如下[16]:
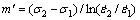 (4)
(4)
式中: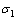 和
和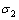 表示同一应变量下应变速率分别为
表示同一应变量下应变速率分别为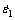 和
和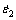 的流变应力。真应变量分别为0.005、0.01、0.025和0.05时不同加载方向下AZ31镁合金的应变速率敏感指数如表2所列。
的流变应力。真应变量分别为0.005、0.01、0.025和0.05时不同加载方向下AZ31镁合金的应变速率敏感指数如表2所列。
表2 轧制态AZ31镁合金沿不同加载方向下的应变速率敏感指数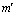
Table 2 Strain rate sensitivity index m′ of rolled AZ31 magnesium alloy loaded along different directions
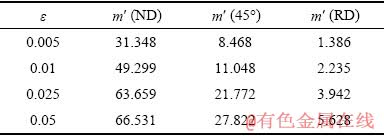
由表2可知,轧制态AZ31镁合金沿ND加载高速冲击载荷时应变速率敏感系数明显高于沿45°和RD方向的,即沿ND加载时具有更强的正应变速率敏感性。
2 Johnson-Cook本构参数确定
Johnson-Cook本构方程是由Johnson和Cook在对多种金属材料特性进行实验研究的基础上提出的经验型本构关系式。Johnson-Cook本构方程简洁直观、各项参数物理意义明显,能够真实反映材料的流变应力与材料所发生应变、应变速率及温度之间的关系,因此在工程实践中得到了广泛的应用[17]。其表达式如下:
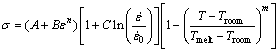 (5)
(5)
式中: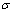 为材料的流变应力;
为材料的流变应力;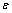 为材料产生变形时的等效塑性应变;
为材料产生变形时的等效塑性应变;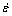 和
和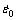 分别表示材料的应变速率和参考应变速率,在本论文中取为准静态应变速率0.001 s-1;T为材料产生变形时的温度;Tmelt和Troom分别表示材料的熔点温度和室温(参考温度)。
分别表示材料的应变速率和参考应变速率,在本论文中取为准静态应变速率0.001 s-1;T为材料产生变形时的温度;Tmelt和Troom分别表示材料的熔点温度和室温(参考温度)。
本构方程中的参数A、B、n、C和m分别称为材料在参考温度下的初始屈服应力、应变硬化系数、应变硬化指数和应变速率系数,均需通过实验来确定[18]。根据各参数的物理意义,J-C本构方程中的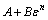 、
、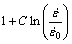 和
和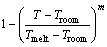 分别称为材料的应变强化项、应变速率强化项和热软化项[19]。由于本文中实验条件为室温,因此热软化项为1,此时Johnson-Cook本构方程表达可简化为
分别称为材料的应变强化项、应变速率强化项和热软化项[19]。由于本文中实验条件为室温,因此热软化项为1,此时Johnson-Cook本构方程表达可简化为
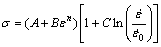 (6)
(6)
为确定J-C本构方程中的参数A、B和n,需对本构方程进行简化。利用INSTRON-4206型液压伺服实验机对轧制态AZ31镁合金沿ND、45°和RD进行应变速率为0.001 s-1的准静态压缩实验,并将0.001 s-1设定为参考应变速率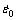 ,此时材料应变速率与参考应变速率相等,应变速率强化项为1,J-C本构方程可进一步简化为式(7)的形式:
,此时材料应变速率与参考应变速率相等,应变速率强化项为1,J-C本构方程可进一步简化为式(7)的形式:
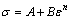 (7)
(7)
轧制态AZ31镁合金在ND、45°和RD加载方向下准静态压缩真应力-真应变曲线与拟合曲线如图7所示。应用式(8)所示非线性最小二乘拟合方法对准静态压缩实验所得到的真应力-真应变曲线进行拟合,计算得出不同加载方向下轧制态AZ31镁合金的A、B和n值(见表3)。
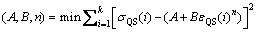 (8)
(8)
在已知A、B和n值的基础上,对不同应变速率下的SHPB实验所得到的真应力-真应变曲线取相同应变的应力值,则Johnson-Cook本构方程中的应变强化项为常数,则此时流变应力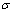 与本构方程中的参数C之间呈线性关系,C值可以通过式(9)所示的最小二乘法取得:
与本构方程中的参数C之间呈线性关系,C值可以通过式(9)所示的最小二乘法取得:
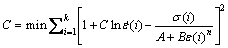 (9)
(9)
图8所示为应用Matlab软件中的最小二乘拟合程序确定参数C的拟合图,图中直线的斜率即为参数C。
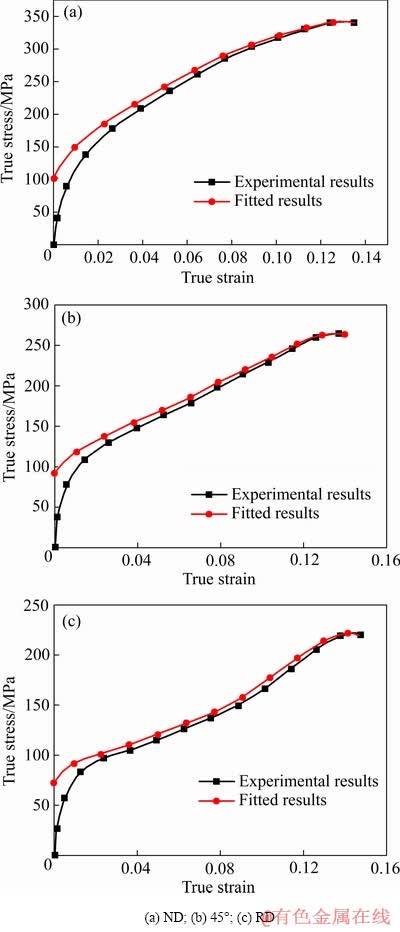
图7 轧制态AZ31镁合金沿不同加载方向下的准静态压缩真应力-应变曲线及拟合曲线
Fig. 7 True stress-strain curves and fitting curves of rolled AZ31 magnesium alloy loaded along different directions at quasi-static compress strain rate
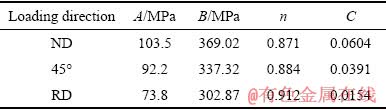
轧制态AZ31镁合金沿不同加载方向的Johnson- Cook本构参数如表3所列。
由Johnson-Cook本构方程参数的拟合结果可知,不同加载方向下其本构参数的变化具有一定的变化规律,初始屈服应力A的变化规律为AND>A45°>ARD;应变硬化系数B的变化规律为BND>B45°>BRD;应变硬化指数n的变化规律为nND>n45°>nRD;应变速率系数C的变化规律为CND>C45°>CRD。
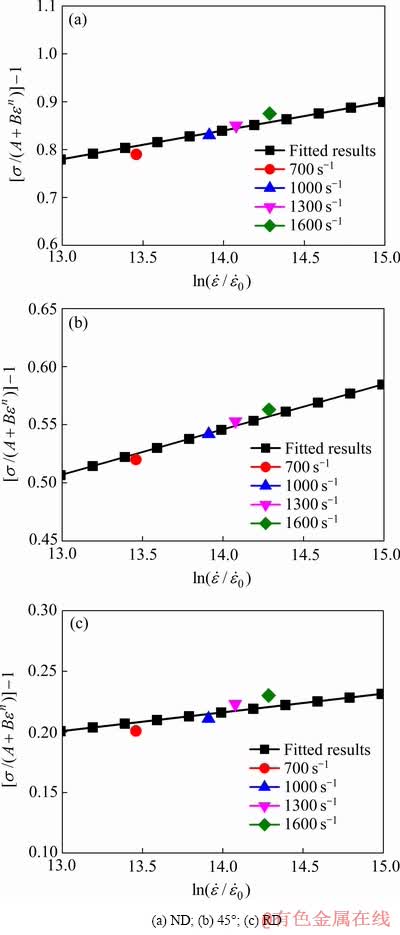
图8 轧制态AZ31镁合金沿不同加载方向下C值拟合结果
Fig. 8 Parameter C fitting results of rolled AZ31 magnesium alloy along different directions
表3 轧制态AZ31镁合金沿不同加载方向下的Johnson-Cook本构参数
Table 3 Johnson-Cook constitutive parameters of rolled AZ31 magnesium alloy along different directions
3 SHPB实验的数值模拟
3.1 前处理与边界条件
SHPB实验数值模拟的前处理由有限元分析专用前处理软件Hypermesh来完成。根据SHPB实验装置中冲击杆、入射杆、试样和透射杆的实际尺寸建立有限元分析模型,由于各部分均为同轴的圆柱状对称结构,为降低计算规模提升求解效率,将数值模拟对象简化为整体模型的1/2。模型中各部分均离散为8节点六面体单元(单元类型solid164),并利用不同的单元组集颜色对冲击杆、入射杆、试样和透射杆进行区分。此外,网格划分过程中还应对入射杆和透射杆表面粘贴应变片处进行标记。前处理共计生成节点52440个、单元60354个,SHPB有限元模型各部分的单元及节点数如表4所列,SHPB有限元模型如图9所示。
表4 SHPB实验有限元模型节点与单元数量
Table 4 Node and element numbers of finite element model for SHPB experiment
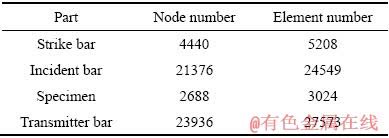
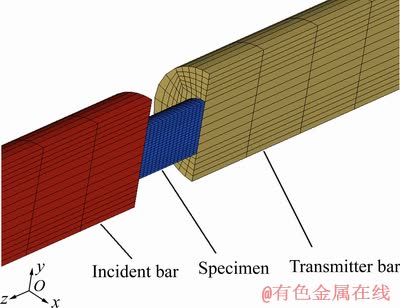
图9 SHPB实验有限元模型图
Fig. 9 Finite element model of SHPB experiment
在有限元分析专用前处理软件Hypermesh的材料属性模板(Material Template)中输入SHPB实验有限元模型各部分的材料参数。冲击杆、入射杆和透射杆均为线弹性钢材料模型,密度为7800 kg/m3,弹性模量为210 GPa,泊松比为0.3;试样的材料参数输入以本研究材料提供方的产品样本中实测值为准,密度为1780 kg/m3,弹性模量为44.8 GPa,泊松比为0.35。采用Johnson-Cook本构方程和Gruneisem状态方程来描述镁合金高速变形的动态响应过程,在Hypermesh所生成的k文件中输入之前拟合得到的Johnson-Cook本构方程参数。
定义SHPB实验的载荷与边界条件如下:有限元模型1/2对称面节点施加对称边界条件;冲击杆节点加载冲击速度(速度值由SHPB实验装置中的激光测速仪测定);在冲击杆与入射杆之间的接触面、入射杆与试样之间的接触面、试样与透射杆之间的接触面定义接触关系(接触类型为:Automatic 3D surface contact);对透射杆后端面节点施加除对称方向以外的约束(本文中为Y、Z方向)。
将SHPB实验有限元模型以.k格式导入到显式动力学分析软件LS-DYNA中,在求解计算前还需定义数值模拟的总求解时间与时间步长。总求解时间的设定应保证入射杆应力波输入端不产生入射波与反射波重叠的现象,即在输入应力脉冲时间内,应力波的传播距离不能超过入射杆长度的2倍。经计算应力波的传播时间≤0.4 ms,因此计算时间设定为0.4 ms即可得到完整的波形图。
3.2 数值模拟结果
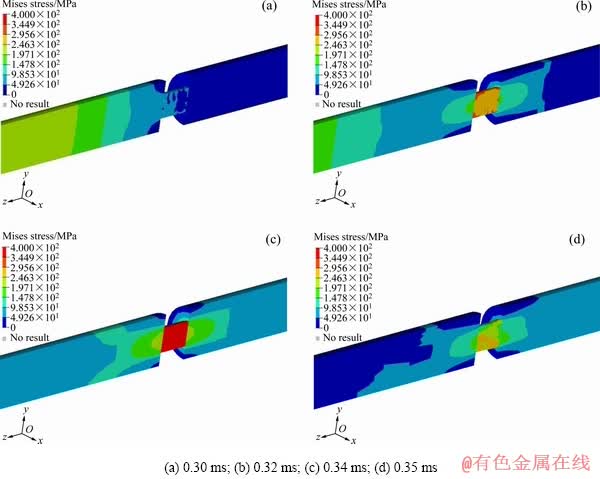
图10 AZ31镁合金沿ND加载1000 s-1冲击载荷时不同时间点的Mises应力分布图
Fig. 10 Mises stress distribution cloud map of AZ31 magnesium alloy loaded along ND at strain rate of 1000 s-1 during different time points
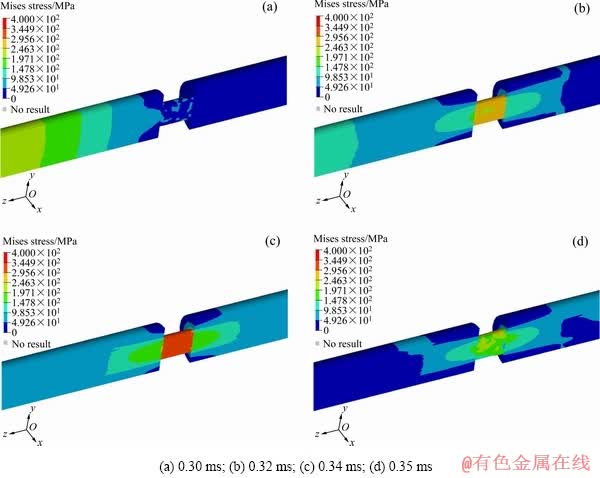
图11 AZ31镁合金沿45°加载1000 s-1冲击载荷时不同时间点的Mises应力分布图
Fig. 11 Mises stress distribution cloud map of AZ31 magnesium alloy loaded along 45° at strain rate of 1000 s-1 during different time points
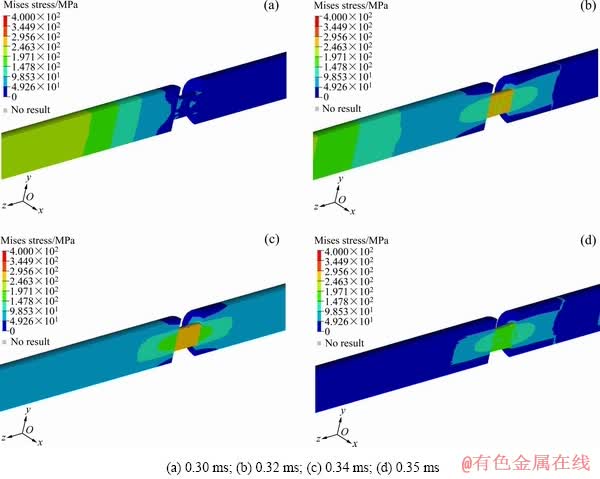
图12 AZ31镁合金沿RD加载1000 s-1冲击载荷时不同时间点的Mises应力分布图
Fig. 12 Mises stress distribution cloud map of AZ31 magnesium alloy loaded along RD at strain rate of 1000 s-1 during different time points
以轧制态AZ31镁合金沿ND加载应变速率为1000 s-1冲击载荷的SHPB实验数值模拟为例,由SHPB实验装置的激光测速结果可知该应变速率对应的冲击杆初始速度为15.6 m/s并将该速度值设定为速度边界条件(Velocity boundary condition),从时间t=0 ms至t=0.295 ms的时间历程中,应力波尚未到达试样,即在该阶段试样上的Mises应力几乎为零。当时间t=0.3 ms时,冲击杆所产生的应力波开始通过入射杆传递到试样与入射杆的交界面产生初始接触应力(Mises应力分布如图10(a)所示);当时间t=0.315~0.34 ms时,经历了应力波的反射与透射,试样进入到均匀变形阶段并在0.34 ms时达到最大应力值(t=0.32 ms和t=0.34 ms对应的Mises应力分布如图10(b)和10(c)所示);t=0.34 ms后随着应力波的扩散,试样开始进入到应力波卸载阶段(t=0.35 ms对应的Mises应力分布如图10(d)所示)。采用相同的方法对沿45°和RD加载应变速率为1000 s-1的SHPB实验进行数值模拟得到t=0.3 ms、0.32 ms、0.34 ms和0.35 ms的Mises应力分布云图(如图11和12所示)。对比轧制态AZ31镁合金沿不同方向进行应变速率为1000 s-1高速变形数值模拟的应力分布云图可知,沿ND加载高速冲击载荷时,试样在应力波输入初始阶段、均匀变形阶段和应力波卸载阶段各单元的Mises应力值及最大应力值均明显高于RD和45°,这是由于沿ND加载时试样变形能力弱于45°和RD,相同应变速率下沿ND高速变形时冲击杆所需的初始动能最大。
为检验数值模拟结果的准确性,对数值模拟后处理结果进行数据提取。选取有限元模型中入射杆与透射杆的中心表面位置节点(节点编号分别为29967和64827,即入射杆与透射杆表面粘贴应变片的位置),提取这两处节点的入射波与透射波的应变-时间曲线。图13~15所示为三种加载方向下AZ31镁合金在应变速率为1000 s-1时入射波形与透射波形的模拟结果与实验结果。经对比可知,数值模拟后处理提取得到的波形与SHPB实验结果具有较高的吻合度。
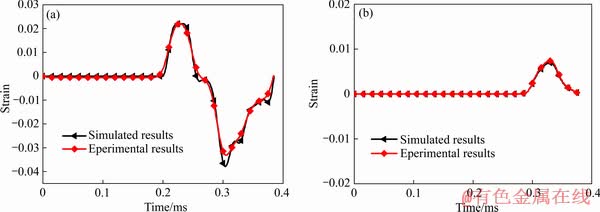
图13 轧制态AZ31镁合金沿ND加载应变速率为1000 s-1冲击载荷的入射与透射波形
Fig. 13 Incident (a) and transmitted (b) strain waves of rolled AZ31 magnesium alloy loaded along ND at strain rate of 1000 s-1
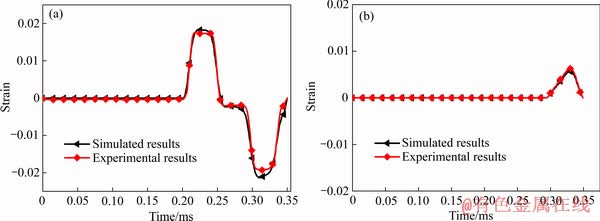
图14 轧制态AZ31镁合金沿45°加载应变速率为1000 s-1冲击载荷的入射与透射波形
Fig. 14 Incident (a) and transmitted (b) strain waves of rolled AZ31 magnesium alloy loaded along 45° at strain rate of 1000 s-1

图15 轧制态AZ31镁合金沿RD加载应变速率为1000 s-1冲击载荷的入射与透射波形
Fig. 15 Incident (a) and transmitted (b) strain waves of rolled AZ31 magnesium alloy loaded along RD at strain rate of 1000 s-1
轧制态AZ31镁合金沿ND、45°和RD加载1000 s-1应变速率冲击载荷的SHPB实验结果、数值模拟结果与拟合结果对比如图16所示。
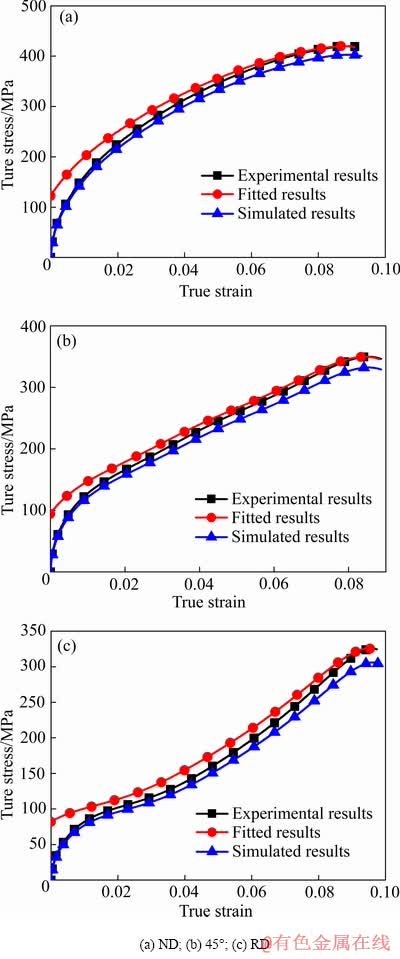
图16 轧制态AZ31镁合金沿不同加载方向在应变速率为1000 s-1时SHPB实验结果、数值模拟与拟合结果的对比
Fig. 16 Comparison among SHPB experimental, numerical simulation and fitted results of rolled AZ31 magnesium alloy loaded along different directions at strain rate of 1000 s-1
由图16可知,采用Johnson-Cook本构方程来描述沿不同加载方向的AZ31镁合金高速变形行为具有较高精度。但随着应变速率的增大,试样的塑性变形量增加会使材料内部产生绝热温升效应和热力学效应,导致形成应变速率与温度叠加的耦合场效应。因此,当应变速率在4000 s-1以上时采用Johnson-Cook本构方程来描述材料的力学性能会存在一定的不足。
4 结论
1) 沿ND、45°和RD对轧制态AZ31镁合金试样进行应变速率分别为700 s-1、1000 s-1、1300 s-1和1600 s-1的SHPB实验,得到不同加载方向和不同应变速率下的真应力-真应变曲线、应变硬化率-真应变曲线以及应变速率敏感指数,并利用非线性最小二乘拟合法得到Johnson-Cook本构方程参数。结果表明:轧制态AZ31镁合金沿不同加载方向的高速变形行为具有明显的各向异性,相比于载荷方向为ND和45°,沿RD加载时AZ31镁合金具有更强的变形能力且真应力-真应变曲线存在明显的屈服阶段;相比于载荷方向为RD和45°,沿ND加载时AZ31镁合金表现出明显的正应变速率强化效应和更强的应变速率敏感性。沿RD高速冲击时所表现出较好的动态压缩性能,这是由于此时冲击加载方向与晶体的c轴相垂直,在较低的临界剪切应力(CRSS)下易产生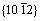 /
/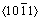 拉伸孪晶,引起基面发生86.3°的旋转从而导致材料发生二次硬化。
拉伸孪晶,引起基面发生86.3°的旋转从而导致材料发生二次硬化。
2) 联合应用有限元分析专用前处理软件Hypermesh与显式动力学分析软件LS-DYNA,建立了AZ31镁合金SHPB实验的有限元模型并进行数值模拟,得到不同加载方向和不同应变速率下SHPB实验的真应变-时间曲线、真应力-真应变曲线和应力波传递过程中各阶段的应力分布云图。经对比可知,数值模拟结果与SHPB实验结果基本一致。研究结果为轧制态AZ31镁合金高速变形行为各向异性的研究提供了重要的手段与理论指导。
REFERENCES
[1] 唐伟琴, 张少睿, 范晓慧, 李大永, 彭颖红. AZ31镁合金的织构对其力学性能的影响[J]. 中国有色金属学报, 2010, 20(3): 371-377.
TANG Wei-qin, ZHANG Shao-rui, FAN Xiao-hui, LI Da-yong, PENG Ying-hong. Texture and its effect on mechanical properties of AZ31 magnesium alloy[J]. The Chinese Journal of Nonferrous Metals, 2010, 20(3): 371-377.
[2] LIU Yan-yu, MAO Ping-li, WANG Feng, LIU Zheng, WANG Zhi. Effect of temperature on the anisotropy of AZ31 magnesium alloy rolling sheet under high strain rate deformation[J]. Philosophical Magazine, 2018, 98: 1068-1086.
[3] 陈振华, 夏伟军, 程永奇, 傅定发. 镁合金织构与各向异性[J]. 中国有色金属学报, 2005, 15(1): 1-10.
CHEN Zhen-hua, XIA Wei-jun, CHENG Yong-qi, FU Ding-fa. Texture and anisotropy in magnesium alloys[J]. The Chinese Journal of Nonferrous Metals, 2005, 15(1): 1-10.
[4] 杨勇彪, 王富耻, 谭成文, 才鸿年. 镁合金动态力学行为研究进展[J]. 兵器材料科学与工程, 2008, 31(3): 71-73.
YANG Yong-biao, WANG Fu-chi, TAN Cheng-wen, CAI Hong-nian. Research progress in dynamic mechanical properties of magnesium alloy[J]. Ordnance Material Science and Engineering, 2008, 31(3): 71-73.
[5] CHINO Y, KIMURA K, HAKAMADA M, MABUCHI M. Mechanical anisotropy due to twinning in an extruded AZ31 Mg alloy[J]. Mater Sci Eng A, 2008, 485(1/2): 311-317.
[6] WATANABE H, ISHIKAWA K. Effect of texture on high temperature deformation behavior at high strain rates in a Mg-3Al-1Zn alloy[J]. Mater Sci Eng A, 2009, 523(1/2): 304.
[7] CHEN Z, BOEHLERT C J. Evaluating the plastic anisotropy of AZ31 using microscopy techniques[J]. JOM, 2013, 65(9): 1237-1244.
[8] 石宝东, 彭 艳, 韩 宇, 刘子龙. AZ31镁合金轧制板材各向异性力学性能研究[J]. 燕山大学学报, 2015, 39(3): 221-225.
SHI Bao-dong, PENG Yan, HAN Yu, LIU Zi-long. Investigation on anisotropic mechanical behavior of AZ31 Mg alloy rolling sheet[J]. Journal of Yanshan University, 2015, 39(3): 221-225.
[9] 毛萍莉, 刘 正, 王长义, 金 鑫, 王 峰, 郭全英, 孙 晶. 高应变速率下AZ31镁合金压缩变形组织[J]. 中国有色金属学报, 2009, 19(5): 817-820.
MAO Ping-li, LIU Zheng, WANG Chang-yi, JIN Xin, WANG Feng, GUO Quan-ying SUN Jing. Deformation micro-structure of AZ31 magnesium alloy under high strain rate compression[J]. The Chinese Journal of Nonferrous Metals, 2009, 19(5): 817-820.
[10] 周 霞, 赵昌美, 李 利, 黄宏军. 基于SHPB实验的挤压AZ91D镁合金动态力学行为数值模拟[J]. 中国有色金属学报, 2014, 24(8): 1968-1975.
ZHOU Xia, ZHAO Chang-mei, LI Li, HUANG Hong-jun. Numerical simulation of dynamic behavior of extruded AZ91D magnesium alloy based on SHPB experiment[J]. The Chinese Journal of Nonferrous Metals, 2014, 24(8): 1968-1975.
[11] 郭鹏程, 曹淑芬, 叶 拓, 刘志文, 李世康, 李落星. 高速冲击载荷下AM80镁合金的力学本构及仿真模拟[J]. 中国有色金属学报, 2017, 27(6): 1075-1082.
GUO Peng-cheng, CAO Shu-fen, YE Tuo, LIU Zhi-wen, LI Shi-kang, LI Luo-xing. Mechanical constitutive equation and simulation of AM80 magnesium alloy under high speed impact load[J]. The Chinese Journal of Nonferrous Metals, 2017, 27(6): 1075-1082.
[12] 刘 正, 董 阳, 毛萍莉, 于金程. 轧制AZ31镁合金板材(4 mm)动态压缩性能与失效行为[J]. 材料工程, 2015, 43(2): 61-66.
LIU Zheng, DONG Yang, MAO Ping-li, YU Jin-cheng. Dynamic compressive properties and failure behaviour of rolled AZ31 magnesium alloy sheet (4 mm)[J]. Journal of Materials Engineering, 2015, 43(2): 61-66.
[13] TAN Cheng-wen, XU Shan-na, WANG Lu, CHEN Zhi-yong, WANG Fu-chi, CAI Hong-nian, Ma Hong-lei. Deformation behavior of AZ31 magnesium alloy at different strain rates and temperatures[J]. Transactions of Nonferrous Metals Society of China, 2007, 17(S1): s347-s352.
[14] 毛萍莉, 于金程, 刘 正, 董 阳, 席 通. 挤压态Mg-Gd-Y 镁合金动态压缩力学性能与失效行为[J]. 中国有色金属学报, 2013, 23(4): 889-897.
MAO Ping-li, YU Jin-cheng, LIU Zheng, DONG Yang, XI Tong. Dynamic mechanical property and failure behavior of extruded Mg-Gd-Y alloy under high strain rate compression[J]. The Chinese Journal of Nonferrous Metals, 2013, 23(4): 889-897.
[15] 张诗昌, 康龙武, 杨 倩, 梅秋平. 压缩条件下AZ31镁合金的力学各向异性[J]. 热加工工艺, 2014, 43(24): 71-75.
ZHANG Shi-chang, KANG Long-wu, YANG Qian, MEI Qiu-ping. Mechanical anisotropy of AZ31 alloy under compression test[J]. Hot Working Technology, 2014, 43(24): 71-75.
[16] LEE W S, TANG Z C. Relationship between mechanical properties and micro-structural response of 6061-T6 aluminum alloy impacted at elevated temperatures[J]. Mater Des, 2014, 58: 116-124.
[17] 滑勇之, 关立文, 刘辛军, 崔海龙. 铝合金7050-T7451高温高应变速率本构方程及修正[J]. 材料工程, 2012(12): 7-13.
HUA Yong-zhi, GUAN Li-wen, LIU Xin-jun, CUI Hai-long. Research and revise on constitutive equation of 7050-T7451 aluminum alloy in high strain rate and high temperature condition[J]. Journal of Materials Engineering, 2012(12): 7-13.
[18] SHI B, ATTIA H. Identification of material constitutive laws for machining-Part Ⅱ: Generation of the constitutive data and validation of the constitutive law[J]. Journal of Manufacturing Science and Engineering, 2010, 132(5): 051009.
[19] UMBRELLO D, SAOUBI R M, OUTEIRO J C. The influence of Johnson-Cook material constants on finite element simulation of machining of AISI 316L steel[J]. International Journal of Machine Tools and Manufacture, 2007, 47(3): 462-470.
High strain rate deformation behaviors experimental study and numerical simulation of rolled AZ31 magnesium alloy loaded along different directions
CHEN Yang, MAO Ping-li, WANG Zhi, LIU Zheng, WANG Rui-feng
(School of Materials Science and Technology, Shenyang University of Technology, Shenyang 110870, China)
Abstract: In order to investigate the isotropic behavior of rolled AZ31 magnesium alloy sheet under high strain rate deformation, the Split Hopkinson Pressure Bar (SHPB) experiments were carried out along normal direction(ND), 45°and rolling direction(RD) at an average strain rate of 700 s-1, 1000 s-1, 1300 s-1 and 1600 s-1, respectively. Based on the experiment results of SHPB, Johnson-Cook constitutive equations of different deformation directions were established. The numerical simulation of SHPB was carried out by jointly using of preprocessing software Hypermesh and explicit dynamics simulation software LS-DYNA. Both experimental and simulation results showed that the rolled AZ31 magnesium alloy along RD has higher deformation ability and the yield stage in true stress-strain curves is more obvious than the other two directions. While ND shows obvious positive strain rate hardening effect and strain rate sensitivity. True strain-time curves and true stress-strain curves obtained by post-processing of numerical simulation are well agreement with the SHPB experimental results. Johnson-Cook constitutive equation parameters of rolled AZ31 magnesium alloy along different loading directions have high precision.
Key words: AZ31 magnesium alloy; high strain rate deformation; isotropic behavior; Johnson-Cook constitutive equation; numerical simulation
Foundation item: Project(51504153) supported by the National Natural Science Foundation of China
Received date: 2019-03-18; Accepted date: 2020-04-28
Corresponding author: MAO Ping-li; Tel: +86-24-25497131; E-mail: maopl@sut.edu.cn
(编辑 王 超)
基金项目:国家自然科学基金资助项目(51504153)
收稿日期:2019-03-18;修订日期:2020-04-28
通信作者:毛萍莉,教授,博士;电话:024-25497131;E-mail:maopl@sut.edu.cn